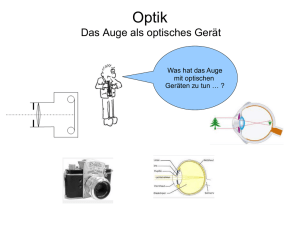
Wichtige optische Elemente und Instrumente:
Werbung

Wichtige optische Elemente und Instrumente: • • • • • • • • • Der aplanatische Meniskus Diffraktive optische Elemente/Linsen Die achromatische Linse = Achromat Der Spektrograph Die Kamera Das menschliche Auge Das Teleskop/Teleskope in der Astronomie Das Mikroskop Anwendung optischer Methoden in der Astronomie: Detektion erdähnlicher Planeten um andere Sterne Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+1 Der aplanatische Meniskus Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+2 Der aplanatische Meniskus Die aplanatischen Punkte einer Kugel: i Behauptung: Eine Kugel mit Radius R und Brechzahl n‘ (schattiert in Grafik) kann alle Punkte auf der äußeren (gestrichelten) Kugel mit Radius n‘R/n (n: Brechzahl des umgebenden Mediums, n<n‘) aberrationsfrei, aber leider nur virtuell, auf die innere (gepunktete) Kugel mit Radius nR/n‘ abbilden. Q i’ O i i’ P’ n’ Betrachte Strahl einer konvergenten Kugelwelle mit Fokuspunkt P. Laut Behauptung muss er nach der Brechung an der Kugel mit Radius R im Punkt Q die lokale optische Achse, gegeben durch die Verbindungslinie OP, im Punkt P‘ auf der gepunkteten Kugel schneiden. n Zu zeigen ist, dass dies gerade dann der Fall ist, wenn für die Brechung das Brechungsgesetz nsini=n‘sini‘ gilt. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+3 P Der aplanatische Meniskus n R OQ R n n' OP' Laut Behauptung gilt: R OP n' R n' OQ n Da die beiden Dreiecke QOP‘ und POQ den gemeinsamen Winkel QOP‘ bzw. QOP haben und das Verhältnis der daran angrenzenden Seiten in beiden Dreiecken identisch ist, müssen die Dreiecke ähnlich sein. i Q i’ O i i’ P’ n’ n Es muss, wie schon in der Grafik eingezeichnet, gelten: Winkel QP‘O ist identisch zum Einfallswinkel i, Winkel QPO ist identisch zum Brechungswinkel i‘. Aus dem Sinussatz im Dreieck POQ folgt (das Verhältnis der Sinusse zweier Winkel ist gleich dem Verhältnis der jeweils gegenüberliegenden Seitenlängen): sin PQO sin i OP n' n sin i n' sin i ' (q.e.d.) sin QPO sin i ' OQ n Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+4 P Der aplanatische Meniskus Der bisher betrachtete Strahl sei nun der Randstrahl eines Strahlbündels, der somit zusammen mit der lokalen optischen Achse die numerische Apertur festlegt. Aus unseren bisherigen Überlegungen folgt dann für das Verhältnis der Sinusse der Aperturwinkel bzw. ‘ des einfallenden konvergenten Strahlbündels bzw. des gebrochenen Strahlbündels: sin ' sin QP' O sin i n' sin sin QPO sin i ' n Der Sinus des Aperturwinkels ‘ des gebrochenen Strahlbündels erhöht sich also um das Verhältnis n‘/n gegenüber dem Sinus des Aperturwinkels des einfallenden Strahlbündels. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+5 Der aplanatische Meniskus Beim aplanatischen Meniskus wird nun die sphärische Rückfläche konzentrisch um den Fokuspunkt P‘ gelegt. Es tritt also keine Richtungsänderung durch Brechung an der Rückfläche mehr auf und insgesamt erhöht der aplanatische Meniskus deshalb die numerische Apertur des einfallenden konvergenten Strahlbündels um den Faktor n‘/n. Umgekehrt kann also durch eine Abfolge mehrerer aplanatischer Menisken die hohe numerische Apertur einer von einem Objektpunkt ausgehenden Kugelwelle erniedrigt werden ohne Aberrationen einzuführen. Für off-axis Objektpunkte treten zwar Aberrationen auf, diese sind aber gering. Geometrische und Technische Optik O j’ P’ j P n’ n n Institut für Optik, Information und N. Lindlein Photonik 126+6 Der aplanatische Meniskus Maximal mit einem aplanatischen Meniskus erreichbare numerische Apertur: Der zum Punkt P laufende Randstrahl des einfallenden Strahlbündels tangiert im Grenzfall des maximalen Aperturwinkels gerade die Kugelfläche (> Halbkugel !), die die Vorderseite des aplanatischen Meniskus bildet, im Punkt Q. Das Dreieck OQP ist dann rechtwinklig am Schnittpunkt Q und es gilt: R n sin n' R n' n n' sin ' sin 1 n Q n n‘ R O j‘ P‘ j P n‘R/n Im Prinzip ist also eine numerische Apertur von bis zu 1.0 in Luft erreichbar. Der Grenzfall ist in der Praxis aber äußerst problematisch, da die Fläche hochgradig entspiegelt sein müsste (streifender Einfall hohe Reflexion) und die Herstellung einer Kugelfläche mit „größer Halbkugel“ auch schwierig ist. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+7 Der aplanatische Meniskus Raytracing Simulation eines aplanatischen Meniskus mit sin‘=0.996, d.h. ‘=84.9o: außen Luft, Linsenmaterial SF10 (n‘=1.723 bei =633 nm), R=100 mm nR/n‘=58.04 mm, n‘R/n=172.3 mm; Krümmungsradius Rückfläche: 50 mm Distances in mm, horizontal z-axis, vertical x-axis -200 -100 0 100 200 150 150 100 100 50 50 0 0 -50 -50 -100 -100 -150 -150 -200 -100 0 100 Seitenansicht Geometrische und Technische Optik 200 Spotdiagramm Institut für Optik, Information und N. Lindlein Photonik 126+8 Der aplanatische Meniskus Raytracing Simulation eines aplanatischen Meniskus mit sin‘=0.996, d.h. ‘=84.9o: außen Luft, Linsenmaterial BK7 (n‘=1.515 bei =633 nm), R=100 mm nR/n‘=66.003 mm, n‘R/n=151.5 mm; Krümmungsradius Rückfläche: 50 mm Auch mit weniger stark brechendem Material ist also eine NA=1.0 erreichbar! Distances in mm, horizontal z-axis, vertical x-axis -200 -100 0 100 200 150 150 100 100 50 50 0 0 -50 -50 -100 -100 -150 -150 -200 -100 0 100 Seitenansicht Geometrische und Technische Optik 200 Spotdiagramm Institut für Optik, Information und N. Lindlein Photonik 126+9 Diffraktive optische Elemente/Linsen Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+10 Diffraktive optische Elemente Wirkungsweisen einiger optischer Elemente Refraktive Optik Brechung an Grenzfläche n1 n2 Diffraktive Optik Brechung in GRadienten INdex Medium Beugung an (lokal) periodischen Strukturen n(r) Beugung an binärem Gitter Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+11 Diffraktive optische Elemente Prinzip eines Beugungsgitters (hier: Amplitudengitter) L sinj j j’ L sinj’ L Geometrische und Technische Optik Konstruktive Interferenz, falls optische Weglängendifferenz (OPD) zwischen äquivalenten Strahlen benachbarter Perioden ganzzahliges Vielfaches m der Wellenlänge ist: sin ' sin m sin ' sin m Institut für Optik, Information und N. Lindlein Photonik 126+12 Diffraktive optische Elemente Zusammenhang Phase und optische Weglänge: Trifft ein Strahl auf eine strukturierte Oberfläche mit einem Dielektrikum mit Brechzahl n (z.B. Quarzglas) auf der einen Seite und Luft auf der anderen Seite, so gilt für die Phasenverzögerung bei einer lokalen Höhe h (bzw. z) des Dielektrikums: x,y n n 1 2 OPD 2 2 OPD=(n1-n2)z(x,y) n 1h z Selbstverständlich gilt diese Gleichung nur für den Fall, dass der einfallende Strahl fast senkrecht auf die lokale Grenzfläche trifft, so dass man annimmt, dass der Strahl seine Richtung nicht ändert. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+13 Diffraktive optische Elemente Beziehung zwischen diffraktiven und refraktiven Strukturen h= /(n-1) Refraktives Element h= /(n-1) Geblaztes (=kontinuierliches) diffraktives Element Anmerkung: Eine geblazte Linse, deren Stufenhöhe h>>/(n-1) ist, ergibt eine Fresnel-Linse. Im Grenzfall sind die einzelnen „Zähne“ dann lokale Prismen. h= /(2(n-1)) Binäres diffraktives Element Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+14 Diffraktive optische Elemente Verschiedene Arten von diffraktiven optischen Elementen a) b) Amplitudengitter Binäres Phasengitter h=/(2(n-1)) Dh Maximal je 1/2=10.1% in ±1. Ordnung (bei 25% in 0. Ordnung) Maximal je 4/2=40.5% in ±1. Ordnung (bei 0% in 0. Ordnung) : Wellenlänge, n: Brechzahl des Gitters, N: Anzahl der Stufen c) Mehrstufiges Phasengitter h=(N-1)/(N(n-1)) d) Geblaztes Phasengitter h=/(n-1) Dh Dh Symmetrie zwischen +1. und -1. Ordnung gebrochen. Je nach Stufenzahl zwischen 40.5% und 100% in 1. Ordnung Geometrische und Technische Optik Theoretisch bis zu 100% in 1. Ordnung (in Praxis selbst bei Entspiegelung weniger) Institut für Optik, Information und N. Lindlein Photonik 126+15 Diffraktive optische Elemente Unterschied Amplitudengitter Phasengitter: Positive Interferenz der Wellen, falls: sin ' sin m sin ' sin m sin Bei binären Phasengittern interferiert auch der rote Strahl positiv, da er wegen der Stufe mit /2 Gangunterschied wieder in Phase ist (für m=1;3;5;…): m OPD m 1 2 2 2 sin ’ sin ’ Geometrische und Technische Optik ’ sin ’ Institut für Optik, Information und N. Lindlein Photonik 126+16 Diffraktive optische Elemente Bei einem binären Phasengitter interferieren also für ungerades m „doppelt so viele Strahlen“ wie bei einem Amplitudengitter positiv. Die Amplitude der Welle in den ungeraden Ordnungen wird doppelt so groß. Die Intensität dieser Ordnungen wird bei einem Phasengitter 4x so groß wie bei einem Amplitudengitter! Anmerkung: Die Energieerhaltung ist natürlich erfüllt, denn beim Amplitudengitter werden 50% der Energie absorbiert und 25% sind in der nullten Beugungsordnung (bei unserem Phasengitter ist dagegen kein Licht in der 0. Ordnung, da dort negative Interferenz auftritt). Beim binären Phasengitter ist 4x so viel Energie für die ungeraden Beugungsordnungen vorhanden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+17 Diffraktive optische Elemente Anschauliche Berechnung der Beugungseffizienz m der einzelnen Ordnungen m bei einem binären Phasengitter mit Tastverhältnis 1:1 (d.h. Stegbreite = Grabenbreite) und Tiefe, die eine optische Weglängendifferenz von /2 zwischen Steg und Graben erzeugt: 0=0: destruktive Interferenz zwischen Licht von Steg und Graben bei Tiefe mit /2 opt. Weglängendifferenz (OPD) 2n=0 (n=1,2,3,): alle geraden Ordnungen (ungleich m=0) fallen aus, da OPD innerhalb von Steg und Graben zwischen Anfang und Ende je ganzzahliges Vielfaches von schon vollständige Auslöschung innerhalb von Steg und Graben sin ’ 1: innerhalb von Steg und Graben OPD zwischen Anfang und Ende nur /2 sin ’ Amplituden addieren sich konstruktiv maximale Effizienz 3=1/9: innerhalb von Steg und Graben OPD zwischen Anfang und Ende 3/2 Amplituden addieren sich nur in einem drittel des Bereiches konstruktiv, Rest löscht sich aus Effizienz nur 1/9 verglichen zu 1. Ordnung (Intensität proportional zu Amplitudenquadrat !). Analog: 5=1/25 bzw. allgemein (2n+1)=1/(2n+1)2 für n=1,2,3,… Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+18 Diffraktive optische Elemente Effizienzen eines binären Phasengitters mit Tastverhältnis 1:1 und idealer Tiefe: Summe der Effizienzen aller Ordnungen muss 1 sein wegen Energieerhaltung 1 4 2 21 1 2 1 0.405 1 1 2 2 8 n 0 2n 1 2 / 8 1 32 1 5 2 5 ... 3 4 2 4 2 0.045 0.016 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+19 Diffraktive optische Elemente Maximale Beugungseffizienz in 1. Ordnung für mehrstufiges Phasengitter mit N Stufen N Effizienz (berechnet in skalarer Näherung) 2 40.5% N 1 N n 1 4 81.1% 8 95.0% Senkrechter Lichteinfall. 16 98.7% Fresnel Reflektionsverluste vernachlässigt. 32 99.7% Ideale Gesamttiefe: d Identische Höhe und Breite aller Stufen. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+20 Diffraktive optische Elemente Diffraktive Linse: Wir betrachten im Folgenden zuerst wieder nur die Meridionalebene und kleine Winkel. Lokale Gitterfrequenz sei proportional zu lateraler Koordinate x: 1 x : cx x Aus Gittergleichung folgt dann für kleine Winkel: sin ' sin m kleine Winkel ' m mcx Gleichung ist analog zu paraxialer Gleichung für die Strahlablenkung an einer Linse mit Brennweite f‘, wenn gilt: 1 1 mc f ' f' mc Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+21 Diffraktive optische Elemente Insbesondere ist für eine diffraktive Linse das Produkt aus Brennweite und Wellenlänge konstant: 0 f ' f ' 0 Die Abbe-Zahl einer diffraktiven Linse ist deshalb: d 1 / f 'd 587.6 nm Vd 3.452 1 / f ' F 1 / f 'C F C 486.1 nm 656.3 nm • Die Abbe-Zahl einer diffraktiven Linse ist also immer konstant, unabhängig vom Material bzw. dem genauen Typ der Linse. • Die Abbe-Zahl einer diffraktiven Linse ist negativ, d.h. ihre Dispersion hat umgekehrtes Vorzeichen wie die von Glas. Der Betrag ist sehr klein, d.h. starke Dispersion! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+22 Diffraktive optische Elemente Phasenfunktion eines diffraktiven optischen Elementes (DOE): Die Phasenfunktion eines DOEs beschreibt, an welchen Stellen sich die lokalen Gitterlinien befinden, d.h. an welchen Stellen die Phase relativ um jeweils 2 zu- oder abnimmt. r r r 0 r r 0 r mit r r r 0 x 2 r 2 y Zusammenhang zwischen der Phasenfunktion und der lokalen Gitterfrequenz , wobei x und y die Koordinaten in der (lokalen) Ebene des DOEs sind: 1 1 x, y x, y x, y 2 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+23 Diffraktive optische Elemente Zusammenhang Höhenprofil h und Phasenfunktion : Geblaztes DOE: h x, y 2 n 1 x, y mod 2 Mehrstufiges Phasen-DOE mit N Stufen: N x , y h x, y floor mod N N n 1 2 x mod a: Modulo-Funktion = Rest bzgl. einer Division von x durch a. floor: Funktion, die die nächst kleinere ganze Zahl zurückgibt. : Wellenlänge im Vakuum, n: Brechzahl des DOEs, wobei außen Luft sei. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+24 Diffraktive optische Elemente Einfache Beispiele einiger wichtiger Phasenfunktionen: Lineares Gitter: x, y 2 ax by Gitterfrequenz konstant: a 2 b 2 Fresnel-Zonen-Linse in paraxialer (parabolischer) Näherung: x, y 2a x 2 y 2 Gitterfrequenz: x, y 2a x 2 y 2 f ' Geometrische und Technische Optik 1 1 mc 2ma Institut für Optik, Information und N. Lindlein Photonik 126+25 Diffraktive optische Elemente Berechnung der Phasenfunktion eines DOE unter Ausnutzung des holographischen Prinzips: Sind die Phase in der auf das DOE einfallenden Wellenfront und die Phase out der gewünschten Wellenfront bekannt, so ergibt sich die Phasenfunktion des Hologramms in der Ordnung m zu: out in m Geometrische und Technische Optik out in m Institut für Optik, Information und N. Lindlein Photonik 126+26 Diffraktive optische Elemente Beispiel: Linse, die einen axialen Punkt im Abstand g vor der Linse auf einen axialen Punkt im Abstand b hinter der Linse im nichtparaxialen Bereich abbilden soll. 2 g2 r2 in m 1 2 b2 r 2 g 2 r 2 2 b2 r 2 out DOE Paraxiale Näherung ergibt unter Object Image Vernachlässigung einer konstanten r point point Phase -2(g+b)/ eine parabolische Funktion: g b 1 1 2 1 1 1 r a b g 2 b g Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+27 Diffraktive optische Elemente Ray tracing Gleichung für lokale Gitter: Plausibilitätsbetrachtung analog zum Brechungsgesetz (multipliziert mit 2/ 2 n2 2 n1 N n2 a 2 n1 a1 0 N a2 N a1 N k 2 N k 1 Interpretation: Die Komponente des k-Vektors senkrecht zu N (i.e. parallel zur Grenzfläche) ist invariant vor und hinter der Grenzfläche. Erweiterung auf diffraktive optische Elemente mit lokalem Gittervektor K mit |K|=2/wobei K in der Grenzfläche liegt, also K·N=0: ganzzahliges Vielfaches m von K muss zur Komponente von k1 senkrecht zu N addiert werden: N k 2 N k1 m N K Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+28 Diffraktive optische Elemente Falls k1, N und K in gemeinsamer Ebene liegen und N senkrecht zu K, ergibt der Betrag der Gleichung die normale Gittergleichung: 2 n2 sin 2 2 n1 sin 1 m 2 n2 sin 2 n1 sin 1 m Allgemeine Gleichung aufgelöst nach a2 ray tracing am DOE: n N k 2 N k 1 m N K N a 2 1 a1 m K 0 n2 2 n2 a2 n1 n a 1 m G N a 2 1 a1 m G N n2 n2 n2 n2 n n 1 2 2 1 a1 N 1 a1 m G n2 n2 n2 mit G : 1 1 K ; G N 0 und G 2 2 2 2 2 n n n n n 2 a 2 1 a1 m G 1 a1 N N sign a1 N 1 1 a1 N 1 m G 2m 12 a1 G N n2 n2 n2 n2 n2 n2 n2 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+29 Diffraktive optische Elemente Ein Spezialfall eines DOE ist ein Holographisch optisches Element (HOE), bei dem der Gittervektor durch die Interferenz zweier Wellen mit lokalen k-Vektoren k1,rec und k2,rec bei der Wellenlänge rec erzeugt wird. Dann lautet die Gleichung für lokale Beugung am HOE: N k 2 N k 1 m N k 2,rec k 1,rec N n2 a 2 n1 a1 m rec N n2,rec a 2,rec n1,rec a1,rec Lens DOE spatial filter HOE HOE Aufnahme Rekonstruktion Lens Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+30 Die achromatische Linse = Achromat Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+31 Der Achromat Definition: Eine achromatische Linse (kurz: Achromat) hat für zwei verschiedene Wellenlängen die gleiche Brennweite. Sie besteht typischerweise aus zwei miteinander verkitteten Einzellinsen. Ihre „Nominalbrennweite“ hat sie aber bei einer dritten Wellenlänge, die normalerweise zwischen den anderen beiden Wellenlängen liegt. Als Wellenlängen mit gleicher Brennweite wählt man für Anwendungen im Sichtbaren Spektrallinien am Rand des sichtbaren Bereichs: F=486.1 nm (blaue Linie des atomaren Wasserstoffs) und C=656.3 nm (rote Linie des atomaren Wasserstoffs). Die Wellenlänge mit Nominalbrennweite ist d=587.6 nm (gelbe Helium-Linie). Analog gibt es noch eine apochromatische Linse (kurz: Apochromat), die für drei verschiedene Wellenlängen gleiche Brennweite hat. Dazu müssen mindestens drei Einzellinsen verwendet werden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+32 Der Achromat Prinzip eines Achromats anhand zweier dünner Linsen, die unmittelbar hintereinander stehen (Idealisierung): Einzellinse: Brennweite f‘i, Brechzahl ni, Krümmungsradien Ri,1 und Ri,2, i=1,2. Brennweite der Linsenkombination f‘, Linsen seien in Luft. Paraxiale Matrix der Linsenkombination: 1 M M 2 M1 1 f '2 1 1 1 f ' f '1 f '2 0 1 1 1 f '1 1 0 1 0 0 1 1 1 1 1 1 f '1 f '2 f' Wellenlängenabhängigkeit der Brechkraft einer Einzellinse: 1 1 : ni 1Ci ni 1 f 'i R R , 1 , 2 i i 1 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+33 Der Achromat Achromasie-Bedingung liefert: 1 f '1 F 1 f '2 F 1 f '1 C 1 f '2 C n1 F 1C1 n2 F 1C2 n1 C 1C1 n2 C 1C2 n1 F n1 C C1 n2 F n2 C C2 Die nur von den Krümmungsradien abhängigen konstanten Terme Ci können durch die Brennweiten bei der mittleren Wellenlänge d ausgedrückt werden: n1 F n1 C n2 F n2 C n1 d 1 f '1 d n2 d 1 f '2 d V1,d f '1 d V2,d f '2 d V1,d und V2,d sind die Abbe-Zahlen der beiden Linsenmaterialien. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+34 Der Achromat Kurze Diskussion der Achromasie-Bedingung: V1,d f '1 d V2,d f '2 d für einen Achromat mit positiver Gesamtbrechkraft f‘>0. 1. Fall: Rein refraktiver Achromat aus zwei refraktiven Linsen. Abbe-Zahlen von Materialien sind immer positiv eine der Linsen muss eine Zerstreuungslinse sein. Da ein stark dispersives Material (Flintglas wie z.B. SF10) eine kleine Abbe-Zahl hat, muss die Brennweite der Linse aus diesem Material betragsmäßig größer sein bzw. die Brechkraft (inverse Brennweite) kleiner als bei der zweiten Linse aus dem schwach dispersiven Material (Kronglas wie z.B. BK7) Für positive Gesamtbrechkraft muss die Kronglaslinse eine Sammellinse und die Flintglaslinse eine Zerstreuungslinse sein. 2. Fall: Achromat aus einer refraktiven und einer diffraktiven Linse (Hybrid-Achromat) Abbe-Zahl einer diffraktiven Linse ist immer negativ und betragsmäßig sehr klein: Vd=-3.452 Sowohl die refraktive als auch diffraktive Linse sind Sammellinsen. Die diffraktive Linse hat aber eine sehr große Brennweite bzw. sehr kleine „Brechkraft“. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+35 Der Achromat Praktische Realisierung eines refraktiven und eines hybriden Achromats mit positiver Gesamtbrechkraft a) b) crown glass Geometrische und Technische Optik flint glass Institut für Optik, Information und N. Lindlein Photonik 126+36 Der Achromat Anmerkungen: Ein refraktiver Achromat aus zwei verkitteten Linsen hat drei Krümmungsradien, von denen nur zwei durch die AchromasieBedingung festgelegt sind. Ein Krümmungsradius kann also frei gewählt werden, was in der Praxis normalerweise dafür benutzt wird, um die Sinus-Bedingung zu erfüllen. Beim hybriden Achromaten kann die Sinus-Bedingung nicht so leicht erfüllt werden, aber dafür kann die diffraktive Linse (freie Wahl der „nicht-parabolischen“ Terme der Phasenfunktion möglich) z.B. die sphärische Aberration (bei einer Wellenlänge, z.B. d) korrigieren. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+37 Der Achromat Design eines Achromaten bei gegebener Brennweite f‘(d): 1 1 1 f ' f '1 f '2 1 f '2 d und V1,d f '1 d V2,d f '2 d V2,d V1,d f '1 d V2,d f '1 d f ' d 1 V1,d bzw. 1 f '1 d V1,d V2,d f '2 d V bzw. f '2 d f ' d 1 1,d V 2,d Beispiele: 1. Refraktiver Achromat aus BK7 (V1,d=64.17) und SF10 (V2,d=28.41) f '1 d 0.557 f ' d und f '2 d 1.259 f ' d 2. Hybrider Achromat aus BK7 (V1,d=64.17) und DOE (V2,d=-3.452) f '1 d 1.054 f ' d und f '2 d 19.588 f ' d 3. Hybrider Achromat aus SF10 (V1,d=28.41) und DOE (V2,d=-3.452) f '1 d 1.122 f ' d und f '2 d 9.230 f ' d Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+38 Der Achromat Restliche Wellenlängen-Abhängigkeit der auf f‘(d) normierten Brennweite f‘: 1 ni 1Ci mit i 1,2 Für refraktiven Achromaten folgt dann: Linse : f 'i V2,d 1 1 1 1 und f '2 d V1,d f '1 d f ' f '1 f '2 V2,d n1 d 1 1 1 C1 C2 V1,d n2 d 1 f '1 d f '2 d f ' 1 1 V2,d f ' d n1 d 11 f '1 f '2 V1,d f ' V2,d n1 d 1 f ' d n1 1 n2 1 V1,d n2 d 1 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+39 Der Achromat Analog folgt für hybriden Achromaten (Linse 1 sei refraktiv und Linse 2 diffraktiv): Linse : DOE : 1 f 'i 1 ni 1Ci mit i 1,2 f 'DOE d f ' DOE d : C DOE Ersetze n2()-1 durch bzw. V2,d durch VDOE,d: VDOE ,d n1 d 11 V1,d f ' V f ' d n1 1 DOE ,d n1 d 1 V1,d d Bei einer einzelnen refraktiven Linse ist die Wellenlängen-Abhängigkeit zum Vergleich: f ' nd 1 f ' d n 1 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+40 Der Achromat Wellenlängenabhängigkeit eines Achromats (refraktiv) bzw. einer Einzellinse Lens (SF10) 1.01 Lens (BK7) Achromatic doublet (BK7+SF10) f’/f’d 1 0.99 0.98 500 Geometrische und Technische Optik 550 l/nm 600 650 Institut für Optik, Information und N. Lindlein Photonik 126+41 Der Achromat Wellenlängenabhängigkeit verschiedener Achromat-Typen 1.001 refractive achromat (BK7+SF10) f’/f’d 1 0.999 hybrid achromat (BK7+DOE) 0.998 0.997 hybrid achromat (SF10+DOE) 0.996 500 Geometrische und Technische Optik 550 l/nm 600 650 Institut für Optik, Information und N. Lindlein Photonik 126+42 Kurzer Einschub zur Auflösung einer Linse oder eines Spiegels Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+43 Auflösungsvermögen einer Linse oder eines Spiegels Exkurs in Wellenoptik: Intensitätsverteilung I() (Airy-Verteilung) des Bildes eines -entfernten Objektes in Brennebene eines Spiegels oder einer Linse mit kreisförmiger Apertur (Durchmesser D, Brennweite f‘, : radiale Koordinate in Brennebene, Wellenlänge Intensität der einfallenden ebenen Welle I0): 1 2 2 J 1 ˆ D D mit ˆ f' ˆ 2 ist die entsprechende Winkel-Koordinate /f‘ f‘ Dj 0.9 [2J1(pr ^)]2 ^)/(pr D I ˆ I 0 4 f ' 2 0.8 0.7 0.6 0.5 0.4 0.3 0.2 D 0.1 r=f‘Dj 0 -3 -2 -1 0 2 ^ r Erste Nullstelle der Airy-Verteilung bei: ˆ 1.22 1.22 Geometrische und Technische Optik 1 D Institut für Optik, Information und N. Lindlein Photonik D 126+44 3 Auflösungsvermögen einer Linse oder eines Spiegels Auflösungsvermögen für zwei Punkte nach Rayleigh: 0.7 0.6 0.5 0.4 0 0.1 Gleiches gilt auch, wenn die Lichtquelle (inkohärent) aus einem schmalen Spalt besteht, dessen Licht kollimiert wird! Intensity (normalized) D 0.3 D 0.2 1.22 0.8 0.9 1 Maximum der Intensität des einen Punktes fällt mit dem ersten Minimum der Intensität des zweiten Punktes zusammen. -0.01 -0.006 -0.002 0 0.002 0.006 x-axis (mm) =/D Geometrische und Technische Optik =1.22 /D Institut für Optik, Information und N. Lindlein Photonik 126+45 0.01 Der Spektrograph Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+46 Der Spektrograph Ein Spektrograph ist ein optisches Instrument, mit dem einfallendes Licht in seine verschiedenen Wellenlängen-Komponenten zerlegt werden kann. Selektiert man am Ausgang des Spektrographen einen schmalen Wellenlängenbereich, so spricht man von einem Monochromator. Eng verwandt mit einem Spektrographen ist auch das Spektrometer, das zur Vermessung des Spektrums verwendet wird und dafür typischerweise einen Spektrographen verwendet. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+47 Der Spektrograph Der Prismen-Spektrograph: Zerlegung des Lichts mit Hilfe eines Prismas a j i i‘ j‘ D‘ D L/2 Generell besteht ein Spektrograph aus einer spalt- oder punktförmigen Lichtquelle, einer Linse zur Kollimation, einem dispersiven Element und einer zweiten Linse zur Abbildung der spalt-/punktförmigen Lichtquelle auf einen Detektor. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+48 Der Spektrograph a Ableitung der spektralen Auflösung (Brechzahl n des Prismas, außen Luft/Vakuum): j sin n sin i n sin i ' sin ' 90 i 90 i ' 180 i i ' o o i j‘ i‘ D‘ o D L/2 sin ' n sin i n sin cos i n cos sin i n sin 1 sin 2 i n cos sin i d ' dn n sin sin n 2 sin 2 cos sin cos ' d n 2 sin 2 d Wichtigster Fall in der Praxis: Symmetrischer Strahlengang, d.h. =‘: sin 1 cos sin n 2 sin 2 sin 2 1 2 cos cos 2 sin 2 n 2 sin 2 sin n sin 2n sin / 2 cos / 2 n sin 21 cos 2 2 2 cos 2 / 2 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+49 Der Spektrograph Natürlich gilt dann (wie vorausgesetzt): sin ' sin n 2 sin 2 cos sin 2 sin / 2 cos / 2 n 2 n 2 sin 2 / 2 2 cos 2 / 2 1 n sin / 2 n sin 2 ACHTUNG: Zur Ableitung der Dispersionsformel muss die vorige Gleichung verwendet werden, da der symmetrische Strahlengang streng nur für eine Wellenlänge möglich ist und man ansonsten die Dispersion bei Brechung an der ersten Grenzfläche des Prismas vernachlässigen würde! 2 sin n sin d ' dn d ' dn dn 2 cos ' 2 sin d d d 2 d n 2 sin 2 d 2 2 1 n sin 2 2 sin dn 2 ' d 2 2 1 n sin 2 Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+50 Der Spektrograph Spektrale Auflösung / wird durch Beugung begrenzt, wenn Spalt genügend klein ist (≤f‘/D): a j Linse mit Brennweite f‘ und Durchmesser D hat Winkelauflösung von Beugung=/D: i i‘ j‘ D‘ Beugung Spektrograph D L/2 2 sin 2 sin dn dn 2 2 D d d D 2 2 2 2 1 n sin 1 n sin 2 2 Alternative Gleichung für spektrale Auflösung (gültig für symmetrischen Strahlengang), die oft verwendet wird: Dabei ist L die Basislänge des 2 sin / 2 dn dn dn Prismas unter der Annahme, dass D 2 D' sin / 2 L cos ' d d d das Prisma voll ausgeleuchtet ist. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+51 Der Spektrograph Der Gitter-Spektrograph: Zerlegung des Lichts mit Hilfe eines Beugungsgitters Spalt sei wieder genügend klein (≤f‘/D), wobei f‘ die Brennweite der beiden Linsen ist. j j’ D’ L D Ableitung der spektralen Auflösung (Periode des Gitters, Beugungsordnung m, außen Luft/Vakuum): sin ' sin m cos ' d ' m m ' Beugung cos ' d D m m D D' Nm cos ' Geometrische und Technische Optik Hierbei ist N die Anzahl der ausgeleuchteten Perioden des Gitters. Institut für Optik, Information und N. Lindlein Photonik 126+52 Der Spektrograph Vergleich Prismen- und Gitter-Spektrograph für praxisnahe Werte: 60o-Prisma aus SF10 (=60o), Schwerpunktswellenlänge =550 nm: n=1.734, dn/d=-0.000161 nm-1, ausgeleuchteter Durchmesser der Linse D=20 mm. Beugungsgitter mit symmetrischem Strahlengang für =-45o Einfallswinkel (m=1): sin ' sin m ' 45o 1 2 2 2 2 389 nm 2 sin dn dn D 2 D 6460 Prisma : 2 d 1 n / 4 d 2 2 1 n sin 2 Gitter-Spektrograph hat m 1 2D D' also ca. 10x höhere Gitter : N 72700 spektrale Auflösung Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+53 Der Spektrograph Für noch höher auflösende Spektrometer werden spezielle auf der Wellenoptik basierende Instrumente eingesetzt. Fabry-Perot-Spektrometer (Vielstrahlinterferenz) oder EchelleSpektrometer erreichen bis zu /=108 Dazu muss aber praktisch immer ein normaler Gitter- oder PrismenSpektrograph vorgeschaltet werden, um nur noch einen kleinen Spektralbereich zu haben. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+54 Die Kamera Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+55 Die Kamera Eine Kamera wird zur Aufnahme des (invertierten) Bildes eines Objektes benutzt. Sie besteht aus folgenden Komponenten: • Linse (Linsensystem!) oder Spiegel mit Brennweite f‘ • Blende (= Aperturblende = kann Fassung Linse/Spiegel sein) • Detektor (z.B. Film, CCD-Chip, …) diaphragm lens photosensitive device Meist ist die Brennweite f‘ sehr viel kleiner als der Abstand des Objektes |dO|. Bildweite dI 1 1 1 d I dO f ' d O f ' Geometrische und Technische Optik dI f ' Institut für Optik, Information und N. Lindlein Photonik 126+56 Die Kamera Die Größe x des Bildes auf dem Kamera-Detektor wird also im wesentlichen durch die Winkelausdehnung des Objektes bestimmt und das Bild ist ungefähr in der Brennebene der Linse: x f ' Beispiel: Kleinbild-Kamera mit f‘=50 mm 1. Aufnahme eines Menschen mit 5 m Abstand (dO=-5 m) von der Kamera und einer Größe von 1.75 m. 1.75 0.35 x f ' 17.5 mm 5 dO f ' 1 1 1 Exakt mit Abbildungsgleichung : 50.51 mm dI d I dO f ' dO f ' dI x 1.75 m 17.68 mm dO Geometrische und Technische Optik Näherungsformel ergibt also nur ca. 1% Fehler. Institut für Optik, Information und N. Lindlein Photonik 126+57 Die Kamera 2. Bild des Mondes aufgenommen mit einer normalen Kleinbild-Kamera mit Brennweite f‘=50 mm: Mond: ≈0.5o x f ' 0.44 mm Auf einem Dia-Film mit 24 mm x 36 mm Größe wäre der Mond also winzig und man könnte kaum Details erkennen (Auflösung z.B. 200 Linien/mm ca. 100 Pixel im Durchmesser) Zur Beobachtung von astronomischen Objekten mit kleiner Winkelausdehnung braucht man lange Brennweiten. Astronomische Kamera mit langbrennweitigem Spiegel. In der Astronomie wird diese oft auch einfach als astronomisches Teleskop bezeichnet. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+58 Die Kamera Die Schärfentiefe: Eine ideale Linse ohne Aberrationen bildet ein Objekt „beugungsbegrenzt“ ab, d.h. die Auflösung wird nur durch die Wellennatur des Lichts bestimmt. Allerdings kann immer nur eine Ebene wirklich scharf abgebildet werden. In einer realen Kamera ist die Auflösung des Detektors oft aber schlechter als die beugungsbegrenzte Auflösung. Auch Objekte in Ebenen mit verschiedener Tiefe können „scharf“ im Sinne der begrenzten Auflösung des Detektors abgebildet werden, solange ein Bildpunkt nicht größer als ein Detektorpixel ist (Detektorpixel = kleinstes noch unterscheidbares Bildelement). Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+59 Die Kamera Schärfentiefe (= Abstand zwischen den noch scharf abgebildeten Ebenen): Durchmesser p der Detektorpixel, Brennweite f‘ der Kamera, Durchmesser D der Blende Objekt- bzw. Bildweite dO bzw. dI der exakt scharf abgebildeten Ebene Objekt- bzw. Bildweite dO,N bzw. dI,N der näher an der Kamera liegenden Ebene, die noch scharf abgebildet wird. Objekt- bzw. Bildweite dO,F bzw. dI,F der weiter von der Kamera entfernt liegenden Ebene, die noch scharf abgebildet wird. ideal object plane detector plane dO,N dI,N D dO dO,F Geometrische und Technische Optik p dI dI,F Institut für Optik, Information und N. Lindlein Photonik 126+60 Die Kamera Blendenzahl/Öffnungszahl f# (f number): f # f' D Blendenzahl bestimmt die Belichtungszeit t, da die auf den Detektor fallende Lichtenergie E proportional zur Fläche der Aperturblende ist (Konstante a). 2 f' E 2 t f # E a t D a t 2 f # af ' 2 Zusammenhang Blendenzahl - numerische Apertur im Bildraum NAI: Gilt nur für weit entfernte Objekte, so dass das Bild ungefähr in der Brennebene der Linse ist. D 1 nI NA I nI sin I nI 2f' 2f# In der Praxis meist nI=1.0 (Luft) NAI=1/(2f#) Es gibt aber auch optische Systeme, bei denen nI≠1.0, wie z.B. im menschlichen Auge! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+61 Die Kamera Ideale Ableitung Schärfentiefe für unterObjektebene schiedliche Brechzahlen nO bzw. nI in Objekt- und Bildraum: nI f ' d O nI nO nI dI d I dO f ' nO f ' nI d O nI f ' d O , N nO nI nI d I ,N d I , N dO, N f' nO f ' nI d O , N nI f ' d O , F n nI n O I d I ,F d I ,F dO,F f' nO f ' nI d O , F Detektorebene dO,N dI,N D dO dO,F p dI dI,F Laut Strahlensatz (siehe Abbildung) gilt: nO f ' d O dO dO,N p D p p nO f ' nI d O 1 p 1 nI d O n f ' d I ,N d I d I ,N O D d I ,N d I ,N d I D D nO f ' nO f ' d O p dO D p d I d I ,F d I ,F dO,F p D d I ,F d I d I ,F nO f ' nO f ' nI d O 1 p 1 nI d O D D nO f ' Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+62 Die Kamera Abbildungsmaßstab für den Fall, dass die Kamera-Linse (in Praxis = Objektiv) die Sinus-Bedingung erfüllt ( Eintritts- und Austrittspupille sind Sphären um Objekt- bzw. Bildpunkt): n sin n D / 2d n d x I xO O O nI sin I O O nI D / 2d I O I nI d O nI nO nI nI d O nI d O 1 nI d O 1 1 Aus Abbildungsgleichung folgt: d I dO f ' nO d I nO f ' nO f ' dO dO p p f# 1 1 D f ' dO dO p p f# 1 1 D f ' dO,N dO,F Geometrische und Technische Optik Für Kamera ist f‘ positiv und negativ (reales invertiertes Bild, da |dO|>f‘ und dO<0). Der Nenner der Gleichung für dO,F kann also Null werden. 1 p p 0 D D d O ,C nO f ' D nO f ' f' 1 1 nI p nI p f # Institut für Optik, Information und N. Lindlein Photonik 126+63 Die Kamera Deutung der letzten Gleichung: nO f ' D nO f ' p f' 1 1 1 0 d.h. d O ,C D nI p nI p f # dO, N d O ,C d O ,C p 2 1 D d O , F Wenn die Kamera auf die „kritische Objektweite“ dO,C scharf gestellt wird, geht |dO,F| gegen unendlich und alle Objekte ab dem Abstand |dO,N|=|dO,C|/2 werden scharf (im Sinn der begrenzten Auflösung des Detektors) abgebildet. Anmerkung: Auch wenn die Kamera auf weiter entfernte Objekte mit Abstand >|dO,C| scharf gestellt wird (d.h. || wird kleiner), werden alle weiter entfernten Objekte scharf abgebildet, da dO,F dann sogar formal positiv wird (wegen 1+p/(D)<0). D.h. sogar virtuelle, durch ein vorgeschaltetes Abbildungssystem erzeugte, Objekte könnten noch scharf abgebildet werden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+64 Die Kamera Beispiel: f‘=50 mm, nO=nI=1, p=11 µm (CCD-Kamera mit großem Dynamikbereich) 1. minimale Blendenzahl f#=2.8 d O ,C d O ,C nO f ' f' 1 81.2 m d O , N 40.6 m nI p f # 2 2. Blendenzahl f#=16 d O ,C d O ,C nO f ' f' 1 14.3 m d O , N 7.1 m nI p f # 2 Aber Vorsicht: Ab dieser Blendenzahl begrenzt die Beugung, die bei der Ableitung der Schärfentiefe nicht berücksichtigt wurde, die Auflösung: rAiry 0.61 NA 1.22 f # 10.7 µm p (für Wellenlänge 550 nm) Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+65 Die Kamera Schärfentiefe für nahe Objekte, so dass dO,F endlich ist: p f# 2d O f ' dO dO 2 p f# p f# p f # 1 1 1 f ' f ' f ' 1 nd wobei rechts verwendet wurde : 1 I O nO f ' d d O , N d O , F 1 1 1 n 2 O p f# 2 nI p f # 1 f ' Für die kritische Distanz (pf#/(f‘)=1) würde der Nenner also wieder Null und d unendlich. Für nähere Objekte (d.h. || wird größer) ist der Nenner natürlich endlich und es gilt näherungsweise: 1 1 1 1 1 n nO nO 1 f ' p f # d 2 O p f # p f p f 2 # 1 2 # 2 2 nI n n p f # I I 1 f ' Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+66 Die Kamera Beispiel für Schärfentiefe bei nahem Objekt: CCD-Kamera mit f‘=50 mm, Linse in Luft, Pixelgröße p=11 µm. Die Blendenzahl sei f#=10 und das Objekt befinde sich in 1 m Abstand, d.h. dO=-1 m Abbildungsmaßstab folgt aus Abbildungsgleichung: 1 Exakte Gleichung für die Schärfentiefe liefert: 1 1 1 n d 2 O p f # 83.746 mm 2 nI p f # 1 f ' Näherungsformel für die Schärfentiefe liefert: 1 1 nO nO 1 d 2 p f# 83.600 mm p f # 1 2 2 nI nI Geometrische und Technische Optik 1 nI d O 0.05263 nO f ' Der relative Fehler der Näherungsformel ist also nur ca. 0.2% und die Schärfentiefe beträgt 8.4 cm bei einer idealen Objektebene in 1 m Abstand. Objekte außerhalb der Schärfentiefe werden unscharf abgebildet. Institut für Optik, Information und N. Lindlein Photonik 126+67 Die Kamera Detektor-Typen: Früher wurden photographische Filme eingesetzt: analog sowohl hinsichtlich der räumlichen Auflösung (es gibt keine Pixel) als auch der Anzahl an Graustufen. CCD oder CMOS-Sensoren: digitale elektronische Detektoren, sowohl räumlich digital (es gibt klar definierte Pixel) als auch bezüglich der Anzahl an Graustufen (Analog-Digital-Wandler erzeugt ein digitales Signal). CCD/CMOS-Sensoren liefern direkt ein elektronisches digitales Signal, das verarbeitet werden kann. Filme dagegen liefern kein elektronisch direkt auswertbares Signal, können dafür aber (nach der Entwicklung und evtl. Umkopierung) ohne Hilfsmittel betrachtet werden. Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+68 Die Kamera Vergleich Film CCD/CMOS-Sensor Film CCD/CMOS Auflösungsvermögen in lp/mm (=Linienpaare/mm) > 1000 lp/mm (s/w), gängig 40-150 lp/mm (Farbe) Pixelabstand 1.7 µm -20 µm Max. 300 lp/mm Anzahl Pixel Pixel nicht vorhanden. Aber: 150 lp/mm bei 36 mm x 24 mm Format ca. 74 MPixel Bis zu 16 MPixel Digital/Analog Räumlich analog, Intensität analog Räumlich digital (Pixel), Intensität digital (DA-Wandler) Quantenausbeute 5-10 % Bis zu ≥ 90% Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+69 Die Kamera Prinzip CCD: CCD=Charge-coupled device Nobelpreis für Physik 2009: Willard Boyle und George E. Smith LadungsverschiebungsVarianten von CCDs „Eimerketten-Prinzip“ Lichtempfindlich ist nur ein Teil jedes Pixels höhere Lichtausbeute möglich durch je eine Mikrolinse pro Pixel. Geometrische und Technische Optik Alles Bildmaterial aus Wikipedia Institut für Optik, Information und N. Lindlein Photonik 126+70 Die Kamera Signal-Rausch-Verhältnis SNR (signal-to-noise) eines CCD-Chips: Jedes Pixel kann je nach Größe nur eine Maximalzahl N an durch einfallende Photonen erzeugten Elektronen speichern. Das Rauschen in der Anzahl der Elektronen liegt typischerweise bei N . Das SNR ist also: N SNR N N Die maximale Anzahl N an speicherbaren Elektronen pro Pixel hängt von der Größe, d.h. Fläche, des Pixels ab. Bei einer Kantenlänge d jedes Pixels gilt also: N d 2 SNR N d Ein CCD-Chip mit 20 µm großen Pixeln hat also beispielsweise ein mehr als 10-fach größeres Signal-Rausch-Verhältnis als ein Chip mit nur 1.7 µm großen Pixeln! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+71 Die Kamera Anmerkungen zur Pixelgröße: Generell sollte man sich klar machen, dass neben dem geringeren Signal-RauschVerhältnis immer kleinere Pixel auch sonst wenig sinnvoll sind, da der Informationsgehalt des Bildes ab einer bestimmten Größe nicht mehr zunimmt. Beugungsbedingte Größe der Airy-Disc (Radius): rAiry 0.61 NA in Luft 0.61 f' rApertur 1.22 f' DApertur 1.22 f # Bei einer Wellenlänge von =0.5 µm wäre der Radius eines Punktbildes also schon durch Beugungseffekte ab einer Blendenzahl von 2.8 größer als 1.7 µm. Pixel mit Durchmesser <1.7 µm können nur noch für Blendenzahlen <2.8 eingesetzt werden, wenn man die volle Auflösung haben möchte. Geringe Schärfentiefe und relativ hohe Anforderungen an das Objektiv bezüglich Aberrationskorrektur wegen des großen Feldwinkels und der kleinen Blendenzahl. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+72 Die Kamera Farb-Kameras: CCD-Chip basierend auf Silizium-Technologie (Standard) besteht letztendlich aus einem Array von Silizium-Photodioden + weiterer Elektronik. Sensitiv für Photonen mit Energie Eph > Bandlücke von Si (EBandlücke=1.1 eV) Wellenlänge : E ph h hc E Bandlücke Si-Photodiode: Strom/einfallende Leistung als Funktion der Wellenlänge Quelle: Wikipedia Geometrische und Technische Optik hc E Bandlücke 6.626 10 34 Js 2.998 108 ms -1 1.127 µm 19 1.1 1.602 10 J CCD-Kamera mit IRdurchlässiger Optik ohne IR-Filter ist bis ins nahe IR sensitiv und liefert „nur Grauwerte“. Institut für Optik, Information und N. Lindlein Photonik 126+73 Die Kamera Farb-Kameras(2): Farb-Kamera hat in der Regel ein Array von Farbfiltern vor dem Chip Verschiedene Pixel für verschiedene Wellenlängenbereiche sensitiv Bayer-Farbfilter: Array mit je einem roten, zwei grünen und einem blauen Pixel (RGB) Quelle: Wikipedia Warum kann man mit nur drei Wellenlängen (bzw. genauer Wellenlängenbereichen) wie beim RGB-Verfahren alle sichtbaren Farben erzeugen bzw. detektieren? Der Grund liegt natürlich in der Physiologie unseres Auges: Wir haben genau drei Farbrezeptoren (S-,M- und L-Zapfen): siehe menschliches Auge Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+74 Das menschliche Auge Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+75 Das menschliche Auge Aufbau des menschlichen Auges (gleiches Prinzip bei allen Wirbeltieraugen): Analogie zu einer Kamera: • Iris = Blende (Durchmesser 2 mm - 8 mm) • Hornhaut + Augenlinse = Linse • Netzhaut = Detektor (schärfstes Sehen in der Netzhautgrube=Sehgrube) Quelle: Zeiss Anmerkung: Maßeinheit für Brechkraft (=1/Brennweite): 1 Dioptrie = 1 dpt = 1 m-1 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+76 Das menschliche Auge Die „Kamera-Linse“ des Auges: Hauptanteil der Brechung findet an der Hornhaut (Cornea) statt (Übergang Luft – Hornhaut: Brechzahldifferenz n=nHornhaut-nLuft=0.376): ca. 43 dpt Augenlinse (Kristalllinse) besteht aus unterschiedlichen Schichten mit Brechzahlen zwischen 1.386 und 1.406 eingebettet in Kammerwasser bzw. Glaskörper mit je nGlaskörper=1.336 n≤0.07 Brechkraft der Linse für entspanntes Auge (Ferne): ca. 19-20 dpt Bei Akkomodation (zusätzliche Brechkraft für nahe Objekte): max. 14 dpt zusätzlich Gesamtbrechkraft Auge: Ferne: 59 dpt (endlicher Abstand Hornhaut zu Linse kleiner als Summe der Einzelbrechkräfte von Hornhaut und Augenlinse) n' f' 59 dpt 16.9 mm f' n' Geometrische und Technische Optik Achtung: Das Auge ist ein Immersionssystem mit n‘=nGlaskörper=1.336. f‘/n‘ ist deshalb die effektive Brennweite bezogen auf Luft. Institut für Optik, Information und N. Lindlein Photonik 126+77 Das menschliche Auge Akkomodation: Fähigkeit des Auges auf unterschiedliche Entfernungen scharf zu stellen. Scharfstellung auf nahes Objekt Ziliarmuskel (Ringmuskel) wird angespannt Ziliarbänder werden entspannt und die elastische Augenlinse versucht möglichst Tröpfchenform anzunehmen stärkere Krümmung = höhere Brechkraft Ziliarmuskel entspannt Ziliarmuskel angespannt Deutliche Sehweite: 25 cm Augenlinse muss zusätzlich 4 dpt Brechkraft liefern Objekt in Ferne dO- Objekt im Abstand der deutlichen Sehweite dO=-25 cm Geometrische und Technische Optik n' n' n' n' n' n n 1 1 dI f1 ' 4 dpt n' n n' dO dO f ' f 2 ' f1 ' d I dO f 2 ' Institut für Optik, Information und N. Lindlein Photonik 126+78 Das menschliche Auge Bei einer zusätzlichen Brechkraft der Augenlinse von 14 dpt (nur in der Jugend) können also noch Objekte im Abstand |dO|=1/14 dpt=7.1 cm scharf gesehen werden. Mit zunehmendem Alter „verkalkt“ die Augenlinse, d.h. ihre Elastizität nimmt ab und deshalb auch ihre Fähigkeit zur Tröpfchenform zusätzliche Brechkraft nimmt ab bis zum „Endstadium“ der zusätzlichen Brechkraft Null. Ab Akkomodationsfähigkeit kleiner als 4 dpt benötigt man eine Lesebrille (im Volksmund „ist der Arm nicht mehr lange genug“ um das Buch weit genug entfernt zu halten). Fachausdruck Presbyopie (Alterssichtigkeit) Diese „natürlichen Alterungsprozesse“ dürfen nicht mit einer angeborenen Fehlsichtigkeit (Ametropie) verwechselt werden, bei der der Augapfel zu kurz (Weitsichtigkeit) oder zu lang (Kurzsichtigkeit) ist. Korrektur der Weitsichtigkeit mit Sammellinse bzw. der Kurzsichtigkeit mit Zerstreuungslinse. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+79 Das menschliche Auge Auflösungsvermögen des menschlichen Auges: Unter optimalen Bedingungen können zwei Objekte mit einem Winkelabstand von =30‘‘ noch unterschieden werden (bei normalsichtigen Augen im Durchschnitt bei 1‘ Winkelabstand). Abstand x der Bildpunkte auf der Netzhaut ist dann: f' x ' f ' 0.5 16.9 mm 2.5 µm n' 180 60 Abstand der „Pixel“ des Auges (= Abstand der Rezeptoren) muss <2.5 µm sein, damit eine Verminderung der Intensität im Punktbild zweier Objektpunkte noch erkennbar ist. Laut Literatur beträgt der Abstand der Rezeptoren (Zapfen) im Zentrum der Sehgrube (Ort des schärfsten Sehens) ca. 1.5-2 µm. Bis Pupillendurchmesser (Irisblende) von ca. 3 mm ist das Auge beugungsbegrenzt: Pupillenradius r=1.5 mm numerische Apertur NA=n‘sin‘=n‘r/f‘=1.5 mm/16.9 mm=0.089 Radius der Airy-Disc für Wellenlänge 550 nm: rAiry=0.61 /NA=3.8 µm Dies wäre sogar größer als der oben berechnete Bildpunktabstand bei optimaler Auflösung, allerdings war dies nur eine Abschätzung, da sowohl etwas kleiner als auch r etwas größer sein können: =450 nm, r=2 mm rAiry=2.3 µm. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+80 Das menschliche Auge Diese Rechnung zeigt auf jeden Fall, dass das menschliche Auge im Lauf der Evolution zu einem erstaunlichen optischen Instrument optimiert wurde, das an den physikalisch möglichen Grenzen funktioniert. Irisblende kann Durchmesser zwischen 2 mm (bei sehr hellem Licht) und 8 mm (bei Dämmerung/Dunkelheit) haben. Mit zunehmendem Pupillendurchmesser (z.B. in der Nacht) verringern Aberrationen (sphärische Aberration wächst mit NA4) das Auflösungsvermögen. Einen wesentlichen Teil unseres „Seh-Apparats“ bildet selbstverständlich die Verarbeitung der Informationen im Gehirn, wobei schon in der Netzhaut (Retina), dem Detektor unseres Auges, eine komplexe Vorverarbeitung durch entsprechende Verschaltung der Nervenzellen (Neuronen) stattfindet. Da dieses System an das Überleben im Alltag eines Primaten angepasst ist, kommt es unter gewissen Umständen zu optischen Täuschungen. Das Auge macht auch ständig bewusste und unbewusste Augenbewegungen um ein Objekt „abzuscannen“, da wir nur in einem sehr schmalen Bereich (ca. 1o) wirklich scharf sehen. Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+81 Das menschliche Auge Farbwahrnehmung: Das menschliche Auge hat unterschiedliche Rezeptoren: Stäbchen: keine Farbempfindlichkeit, d.h. nur Schwarz-Weiß-Sehen, aber extrem empfindlich (bis zu einzelne Photonen sichtbar) Nachtsehen (skotopisches Sehen) erfolgt mit Stäbchen. Häufigkeit auf der Netzhaut nimmt vom Zentrum zum Rand hin zu (ca. 120 Millionen insgesamt) Mensch sieht bei Dämmerung in der Peripherie besser. Zapfen: Farbrezeptoren durch drei Zapfen-Typen: S-Zapfen (blau), M-Zapfen (grün) und L-Zapfen (rot). Zapfen benötigen mindestens 200 Photonen für ein zuverlässiges Signal Zapfen nur bei Tageslicht aktiv (photopisches Sehen), bei geringer Helligkeit wie nachts „abgeschaltet“, d.h. keine Farbwahrnehmung. Häufigkeit nimmt vom Zentrum der Netzhaut zum Rand hin ab. Höchste Dichte in der fovea centralis=Sehgrube (ca. 6 Millionen insgesamt auf der menschlichen Netzhaut, davon ca. 200 000 in der Sehgrube mit ca. 1.5 mm Durchmesser). Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+82 Das menschliche Auge Verteilung der Zapfen (blau) und Stäbchen (rot) auf der Netzhaut: In Sehgrube praktisch nur Zapfen, größte Dichte der Stäbchen auf Ring mit 17o Winkelabstand relativ zur optischen Achse. Da im Zentrum der Sehgrube (fast) keine Stäbchen vorhanden sind und bei Dunkelheit die Zapfen nicht mehr funktionieren, kann man bei Dunkelheit nur unscharf sehen und z.B. kaum einen Text lesen. Der blinde Fleck (Austrittspunkt des Sehnervs) ist weiß gezeichnet (rechts von der Sehgrube). Quelle: http://www.dma.ufg.ac.at/app/link/Grundlagen:Allgemeine/module/16457?step=2 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+83 Das menschliche Auge Farbwahrnehmung(2): WellenlängenAbhängigkeit der Empfindlichkeit der verschiedenen Rezeptoren im menschlichen Auge (für jeden Rezeptor getrennt normiert) S,M,L: Zapfen-Typen R: Stäbchen (engl. rods) Quelle: Wikipedia Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+84 Das menschliche Auge Farbwahrnehmung(3): Relative Empfindlichkeit der verschiedenen Zapfen bzw. der Gesamtheit der Zapfen in der Sehgrube im menschlichen Auge S,M,L: Zapfen-Typen Z: Sehgrube Maximale Empfindlichkeit des Auges bei 555 nm (Tagessehen) bzw. 498 nm (Nachtsehen) ist also gut an das Strahlungsmaximum unserer Sonne bei ca. 500 nm angepasst! Geometrische und Technische Optik Quelle: Wikipedia Institut für Optik, Information und N. Lindlein Photonik 126+85 Das menschliche Auge Rot-Grün-Sehschwäche bzw. totale Farbenblindheit: Quelle: Wikipedia Bei Rot-Grün-Sehschwäche (bis zu 9% der Männer und 0.8% der Frauen) kann man Rot und Grün nicht unterscheiden, da anstelle der M- und L-Zapfen nur eine Sorte vorliegt. Fehlen die Zapfen vollständig (recht selten) kann man nur noch mit Hilfe der Stäbchen Grautöne wahrnehmen und ist meist extrem behindert (Stäbchen am Tag geblendet, in Sehgrube meist nur geringe Stäbchendichte und Sehschärfe). Nachweis der Rot-Grün-Sehschwäche Geometrische und Technische Optik Simulation der Rot-Grün-Sehschwäche (Mitte) bzw. totaler Farbenblindheit (rechts) für Normalsichtigen Institut für Optik, Information und N. Lindlein Photonik 126+86 Das menschliche Auge Der RGB-Farbraum: Durch additive Mischung unterschiedlicher Intensitäten von nur drei Grundfarben (rot, grün und blau), die in etwa an die Absorptionsmaxima der drei Zapfen-Typen angepasst sind, lassen sich alle Farbtöne für das menschliche Auge erzeugen, da das Auge eben nur über das Verhältnis der Anregung der drei Zapfen-Typen Farben erkennen kann. Wenn wir auf einem Computer-Bildschirm z.B. gelbes Licht sehen, so wurde dort nicht etwa wirklich monochromatisches Licht mit einer Wellenlänge emittiert, die wir als gelb empfinden, sondern es wurde durch die Mischung von rotem und grünem Licht erzeugt. Diese Eigenschaft unseres Farbwahrnehmungs-Systems mit den drei ZapfenTypen ermöglicht also erst die technische Darstellung aller Farben. In der Drucktechnik muss man natürlich die subtraktive Farbmischung verwenden, bei der aus weißem Licht (= Mischung aller Farben) entsprechende Farben herausgefiltert werden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+87 Das menschliche Auge Anmerkung zur Farbwahrnehmung anderer Tiere: Manche Tiere haben bis zu 4 Farb-Rezeptoren (Vögel, Fische). Manche Tiere wie Vögel, (manche) Fische und Schmetterlinge sehen im Ultravioletten bei unter 400 nm. Die meisten Säugetiere (Ausnahme Primaten wie z.B. der Mensch) haben nur 2 Farb-Rezeptoren. Mensch Biene Fisch (Plötze) Quelle: http://www.sinnesphysiologie.de/komplex/farbe.htm Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+88 Das Teleskop Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+89 Das Teleskop Definition: Ein Teleskop ist ein System aus zwei Linsen (oder Spiegeln), bei dem der bildseitige Brennpunkt der ersten Linse (Objektiv) mit dem objektseitigen Brennpunkt der zweiten Linse (Okular) zusammenfällt. Es gibt zwei unterschiedliche Arten: a) Kepler-Teleskop (astronomisches Fernrohr) aus zwei Sammellinsen b) Galilei-Teleskop (terrestrisches Fernrohr, holländisches Fernrohr) aus einer Sammel- und einer Zerstreuungslinse Geometrische und Technische Optik (a) u2 u2’ u1 u1’ -f2=f2’ F1’=F2 f1’ (b) u1 u1’ u2 u2’ F1’=F2 f2 f1’ Institut für Optik, Information und N. Lindlein Photonik 126+90 Das Teleskop Paraxiale Matrix eines Teleskops: Bildseitige Brennweite f1‘ der ersten Linse bzw. f2‘ der zweiten Linse, je in Luft. Laut Definition gilt für Abstand d zwischen bildseitiger Hauptebene der ersten Linse und objektseitiger Hauptebene der zweiten Linse: d f1 ' f 2 f1 ' f 2 ' d f2 ' d 1 0 1 d 1 0 1 f1 ' f1 ' 1 1 M 1 1 1 0 1 d d 1 f f ' ' 1 0 1 2 f2 ' f1 ' f 2 ' f1 ' f 2 ' f1 ' f 2 ' f1 ' f 2 ' M: Matrix des Teleskops von objektseitiger Hauptebene U1 der ersten Linse bis zur bildseitigen Hauptebene U2‘ der zweiten Linse. Die Brechkraft (Koeffizient -C) ist also bei einem Teleskop Null bzw. die Brennweite ist unendlich (daher auch der Name afokales System für ein Teleskop)! Trotzdem kann ein Teleskop aber zur Abbildung von Objekten verwendet werden! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+91 Das Teleskop Teleskop als Aufweitungssystem und Abbildungssystem für weit entfernte Objekte Betrachte einfallende ebene Welle unter Winkel relativ zur optischen Achse paraxiales Strahlenbündel wird durch zwei Strahlen der Höhe x1 bzw. x2 vor dem Teleskop und dem Winkel repräsentiert. Die Strahlvektoren unmittelbar hinter dem Teleskop sind dann: f2 ' xi f1 ' f 2 'i xi ' xi f1 ' mit i 1,2 M f1 ' i ' i i ' f 2 ' f' f' ' 1 ' 2 ' 1 1 f2 ' f2 ' x' 1 f2 ' f2 ' x': x2 ' x1 ' x2 x1 x x f1 ' f1 ' Geometrische und Technische Optik Die Winkelvergrößerung ist also betragsmäßig gleich dem Verhältnis der Brennweiten f1‘/f2‘. Eine einfallende ebene Welle mit Durchmesser x wird um den Faktor –f2‘/f1‘= =1/ aufgeweitet (oder komprimiert). Institut für Optik, Information und N. Lindlein Photonik 126+92 Das Teleskop Für |f1‘|>|f2‘| wird die Winkelvergrößerung also betragsmäßig größer als eins und das entfernte Objekt erscheint unter einem vergrößerten Winkel, d.h. auch größer. Bei einem Kepler-Teleskop gilt f1‘>0 und f2‘>0 <0, d.h. das Bild steht auf dem Kopf. Bei astronomischen Objekten ist dies kein Problem, bei terrestrischen Objekten ist es aber störend, so dass man ein Bildumkehrungs-System benutzen muss (z.B. nachgeschaltetes Kepler-Teleskop mit zwei identischen Linsen). Bei einem vergrößernden Galilei-Teleskop gilt f1‘>0 und f2‘<0 >0, d.h. das Bild steht aufrecht. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+93 Das Teleskop Abbildung endlich weit entfernter Objekte mit einem Teleskop u2 u2’ u1 u1 ’ Das Objekt befinde sich in der Entfernung d1 vor der objektseitigen Hauptebene der ersten d1 -f2=f2’ Linse (d1>0, wenn Objekt links der ersten d2 F1’=F2 Linse ist). Das Bild ist dann in der Entfernung d2 hinter der bildseitigen Hauptebene der f1’ Image zweiten Linse, wobei es reell ist, wenn d2>0 Object plane plane gilt. Matrix M‘ von Objekt- zu Bildebene ist: f2 ' d 1 f1 ' 2 M ' 0 1 0 f2 ' f1 ' f 2 ' d 1 1 f1 ' f1 ' 0 1 0 f2 ' Für Abbildung muss der „B-Koeffizient“ Null sein: f2 ' f ' d2 1 f1 ' f2 ' f1 ' f2 ' f1 ' f 2 'd1 f ' f ' f' f ' f1 ' f 2 'd1 2 d 2 1 0 d 2 f 2 ' 2 d1 2 2 f1 ' f2 ' f1 ' f1 ' 2 Geometrische und Technische Optik 2 Institut für Optik, Information und N. Lindlein Photonik 126+94 Das Teleskop Um also ein reelles Bild (d.h. d2≥0) eines reellen Objektes (d1≥0) zu erzeugen, muss gelten: 2 2 2 d 2 f 2 ' f 2 ' f1 ' d1 f 2 ' f1 '2 0 f1 ' f1 ' f2 ' d1 0 1 1 0 f1 ' f 2 ' Da bei einem Galilei-Fernrohr die Sammellinse immer die betragsmäßig größere Brennweite haben muss (siehe später), kann ein Galilei-Fernrohr kein reelles Bild eines reellen Objektes liefern. Das Kepler-Teleskop liefert dagegen ein reelles Bild solange 0≤d1≤f1‘+(f1‘)2/f2‘ gilt. Im Fall der teleskopischen Abbildung gilt für den lateralen Abbildungsmaßstab : x' Ax B B 0 f ' A 2 x x f1 ' Der Abbildungsmaßstab hängt also nur vom Verhältnis der Brennweiten ab und nicht von der Lage des Objektes. Wenn sich in der gemeinsamen Brennebene des Teleskops (nur Kepler) noch die Aperturblende befindet, ist das System telezentrisch. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+95 Das Teleskop Wichtiges teleskopisches Abbildungssystem: Das 4f-System Ein wichtiger Spezialfall eines teleskopischen Abbildungssystems ist das sogenannte 4f-System, bei dem beide Linsen die gleiche Brennweite f1‘=f2‘=f‘>0 besitzen. f '2 f '2 d 2 f 2 ' 2 f1 ' d1 2 f1 ' 2 2 f 'd1 d1 d 2 2 f ' f2 ' 1 f1 ' Bei einem 4f-System (Gesamtlänge 4f‘) ist also die Summe der Abstände des Objektes und des Bildes von den Linsen konstant bzw. man kann das Teleskop axial verschieben, ohne dass sich paraxial etwas an der Abbildungssituation ändert (bei einem realen System ändern sich natürlich eventuelle Aberrationen!). Das Bild hat die gleiche Größe wie das Objekt, steht aber auf dem Kopf. 4f-Systeme werden z.B. verwendet, um ein nicht direkt zugängliches Zwischenbild reell abzubilden und damit zugänglich zu machen. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+96 Das Teleskop Apertur- und Feldblende eines teleskopischen Abbildungssystems (Kepler-Teleskop) (a) Infinite distant objects aperture stop field stop Bei unendlich weit entfernten Objekten ist in der Regel die Apertur der ersten Linse die Aperturblende. Die Feldblende bringt man sinnvollerweise in der gemeinsamen Brennebene des (Kepler-)Teleskops an. Bei einem Objekt in der vorderen Brennebene der ersten Linse ist die Apertur der ersten Linse die Feldblende, während eine Blende in der gemeinsamen Brennebene des Teleskops zur Aperturblende wird. Es tritt allerdings Vignettierung am Rand des Feldes auf. Geometrische und Technische Optik (b) Finite distant objects field stop vignetted image point aperture stop Institut für Optik, Information und N. Lindlein Photonik 126+97 Das Teleskop Berechnung der Austrittspupille bei Kepler- und Galilei-Teleskop für entfernte Objekte und den Fall, dass die Apertur des Objektivs mit Durchmesser D die Aperturblende ist. Eintrittspupille fällt dann mit der Apertur des Objektivs zusammen und die Austrittspupille ist das Bild davon abgebildet durch das Okular mit Brennweite f2‘. Die Objektweite dO und Bildweite dI der Abbildung lauten also: d O f1 ' f 2 ' f ' f ' f ' 1 1 1 dI 2 1 2 d I dO f 2 ' f1 ' Austrittspupille f1 ' f 2 ' f2 ' f 2 ' f1 ' f 2 ' d f ' 1 f1 ' I 2 dO f1 ' f1 ' f 2 ' Die Bildweite der Austrittspupille ist also ungefähr gleich der Brennweite des Okulars und der Durchmesser der Austrittspupille ist D/||. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+98 Das Teleskop Anmerkungen zum Kepler-Teleskop: Kepler-Teleskop zur vergrößerten Abbildung ferner Objekte besteht aus dem Objektiv (erste Linse) und dem Okular (zweite Linse), die beide Sammellinsen sind. In der hinteren Brennebene des Objektivs entsteht ein reelles Bild des Objekts und hinter dem Okular ergibt sich wiederum ein Bild im Unendlichen, aber mit vergrößertem Sehwinkel, da f1‘>f2‘. Die Aperturblende des Kepler-Teleskops ist die Apertur des Objektivs mit Durchmesser D, solange die Apertur des Okulars groß genug ist. Wegen des deutlich geringeren Strahlquerschnitts am Okular (für ||>>1) muss die Apertur des Okulars allerdings absolut gesehen nicht sehr groß sein. Eintrittspupille des Teleskops = Apertur des Objektivs Austrittspupille als Bild der Aperturblende liegt nahe der hinteren Brennebene des Okulars wegen f1‘>>f2‘ und hat einen Durchmesser D/||. Die Pupille des Auges kann mit der Austrittspupille zur Deckung gebracht werden, so dass alles Licht, das das Objektiv trifft, auch auf die Netzhaut fällt, falls Durchmesser DAuge der Augenpupille DAuge>D/||. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+99 Das Teleskop Anmerkungen zum Galilei-Teleskop: Generell muss beim Galilei-Teleskop die Sammellinse die betragsmäßig größere Brennweite als die Zerstreuungslinse haben wegen: d f1 ' f 2 ' 0 f1 ' f 2 ' 1. Fall : f1 ' 0 f 2 ' 0 f 2 ' f 2 ' f1 ' f1 ' 2. Fall : f1 ' 0 f 2 ' 0 f1 ' f1 ' f 2 ' f 2 ' Vorteile sind: Die kompakte Baulänge von |f1‘|-|f2‘| verglichen mit |f1‘|+|f2‘| beim Kepler-Teleskop. Das aufrecht stehende Bild eines entfernten Objektes. Großer Nachteil ist (nur der Fall der Sammellinse als Objektiv wird betrachtet): Die Austrittspupille als Bild der Apertur des Objektivs abgebildet mit dem Okular liegt vor dem Okular, da dI≈f2‘<0. Die Augenpupille kann deshalb nicht an den Ort der Austrittspupille gebracht werden und man hat einen „Schlüsselloch-Effekt“, der das Feld stark einschränkt. Es sind in der Praxis auch nur Winkelvergrößerungen von 2-5 sinnvoll. Sinnvolle Anwendungen: Strahlaufweitung, Opernglas Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+100 Teleskope in der Astronomie Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+101 Teleskope in der Astronomie Teleskope in der Astronomie (=„astronomisches Teleskop“): Begriffsklärung: Ein modernes Teleskop in der Astronomie bildet mit Hilfe einer Linse, eines Spiegels oder auch eines ganzen optischen Systems (Objektiv) ein reelles Bild eines unendlich weit entfernten Objekts auf einem Detektor (CCD, fotografischer Film). Die Apertur des Objektivs ist meist auch gleichzeitig die Aperturblende. Laut unserer Definition ist ein modernes astronomisches Teleskop also streng genommen eine Kamera. Ein astronomisches Hobby-Teleskop hat dagegen keinen unmittelbaren Detektor sondern stattdessen ein Okular zur visuellen Beobachtung, so dass Objektiv und Okular zusammen ein Kepler-Teleskop bilden. Die astronomische Kamera bezeichnet in der Astronomie einfach ein normales modernes astronomisches Teleskop mit großem Feldwinkel, das keine direkte visuelle Beobachtung mit dem Auge zulässt. (Anmerkung: professionelle astronomische Teleskope lassen allerdings praktisch nie mehr eine direkte visuelle Beobachtung mit dem Auge zu.) Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+102 Teleskope in der Astronomie Linsen-Teleskope (sogenannte Refraktoren) werden heutzutage nur noch selten in der Astronomie eingesetzt, da Linsen mit großen Durchmessern (und deshalb großer Dicke) sehr massiv und teuer sind. In der Praxis verwendet man deshalb fast nur noch Spiegel-Teleskope. Beliebte Bauweisen (heutzutage besonders in der Hobby-Astronomie) sind das Newton-Teleskop (auch Newton Reflektor genannt) und das Cassegrain-Teleskop bzw. das Schmidt-Cassegrain-Teleskop. Eine verbesserte Version des Cassegrain-Teleskops ist das Ritchey-ChrétienCassegrain-Teleskop, das auch bei sehr großen Teleskopen verwendet wird: • Hubble-Space-Teleskop (Primärspiegel mit 2.4 m Durchmesser und effektiver Brennweite von 57.6 m) • Very Large Telescope (VLT) der ESO in Chile (vier baugleiche zusammen geschaltete Teleskope mit je 8.2 m Primärspiegeldurchmesser und effektiver Brennweite von 108.8 m) Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+103 Teleskope in der Astronomie Einschub: Kegelschnitte Kegelschnitte entstehen beim Schnitt eines (unendlichen) (Doppel-)Kreiskegels mit einer Ebene. Kategorien: • Ellipse mit Spezialfall Kreis (Kreis Winkel zwischen Ebene und Kegelachse ist 90 Grad, Ellipse Winkel zwischen Ebene und Kegelachse größer als Kegelwinkel) • Parabel ( Ebene parallel zum Kegelmantel, d.h. Winkel zwischen Ebene und Kegelachse gleich Kegelwinkel) Quelle: Wikipedia • Hyperbel ( Winkel zwischen Ebene und Kegelachse kleiner als Kegelwinkel) Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+104 Teleskope in der Astronomie Brennpunkte eines Kegelschnitts Kegelschnitte sind durch zwei sogenannte Brennpunkte definiert. Ellipse und Parabel: Die Summe der Abstände von den beiden Brennpunkten ist für alle Punkte der Ellipse/Parabel identisch. Bei der Parabel ist allerdings einer der Brennpunkte im Unendlichen. Hyperbel: Die Differenz der Abstände von den beiden Brennpunkten ist für alle Punkte der Hyperbel identisch. Quelle: Wikipedia Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+105 Teleskope in der Astronomie Dreht man den Kegelschnitt um seine Symmetrieachse, so entstehen: • Rotationsellipsoid (Spezialfall Kugel), • Rotationsparaboloid • Rotationshyperboloid Als Spiegel haben diese Körper die Eigenschaft, dass alle Lichtstrahlen, die vom einen Brennpunkt ausgehen und am Spiegel reflektiert wurden, im anderen Brennpunkt fokussieren (für Ellipsoid und Paraboloid) oder von ihm ausgehen zu scheinen (für Hyperboloid). ACHTUNG: Die Brennpunkte des Kegelschnitts haben im Allgemeinen nichts mit den optischen Brennpunkten des Spiegels im Sinn der paraxialen Optik zu tun. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+106 Teleskope in der Astronomie Zusammenhang mit der in der Optik üblichen Asphärenformel: Konische Konstante K, Scheitelkrümmung C=1/R (R: Scheitelkrümmungsradius), radiale Koordinate r, axiale Koordinate z 1 1 K 1C 2 r 2 z r 2 2 K 1 K 1C 1 1 K 1C r Cr 2 C 0 1 K 1C 2 r 2 1 K 1Cz K 1Cz 12 K 1C 2 r 2 1 2 1. Fall: 2. Fall: 2 z r K 1 K 1 0 1 2 1 a b 2 2 z r K 1 K 1 0 1 2 1 a b Ellipsoid Hyperboloid Scheitel sind jeweils bei z=0 (oder z=2a) Halbachsen a und b: Geometrische und Technische Optik 1 R a ; b K 1C K 1 1 K 1 C R K 1 Institut für Optik, Information und N. Lindlein Photonik 126+107 Teleskope in der Astronomie r Ellipsoid: Entfernung e zwischen Brennpunkt und Scheitel a a e2 b 2 a e a 2 b2 e a a2 b2 R2 R2 R 1 K 2 K 1 K 1 K 1 R e K 1 F1 b a F2 Achtung: Für K ist nur der Wertebereich -1<K0 zugelassen. Kurven mit K>0 sind keine Ellipsoide mit aberrationsfreier Abbildung zwischen den Brennpunkten! e Hyperboloid: Entfernung e zwischen Brennpunkt und Scheitel (ohne Beweis) 2 2 2 2 R e a a b K 1 2 2 R 1 K K 1 R R R 2 K 1 K 1 K 1 R R 2 K 1 K 1 D.h. gleiche Abhängigkeit wie bei Ellipsoid! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+108 z Teleskope in der Astronomie Für Ellipsoid und Hyperboloid (und im Grenzfall auch für Paraboloid) gilt also für die Entfernung e zwischen Brennpunkt und Scheitel: R 1 K e K 1 wegen K 0 R 1 K 1 K 2 R 1 K R 1 K 1 K 1 K Dabei sind für K nur Werte K0 zugelassen, da Kurven mit K>0 kein Ellipsoid ergeben, dessen Symmetrieachse (=Drehachse) parallel zur Verbindungslinie zwischen den beiden Brennpunkten ist! K>0 große Halbachse der Ellipse in Richtung der Koordinate r, Drehung der Ellipse erfolgt aber um die z-Achse Keine aberrationsfreie Abbildung zwischen den beiden Brennpunkten! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+109 Teleskope in der Astronomie Grenzfall Paraboloid: K -1 bzw. -K +1 R e 1 K K 1 R / 1 K R / 1 K R / 2 Der eine Brennpunkt liegt also, wie schon früher gesagt, im Unendlichen. Der andere Brennpunkt liegt im Abstand R/2 vom Scheitel. Distances in mm, horizontal z-axis, vertical x-axis Für einen konkaven Parabolspiegel (R<0), ist aber die bildseitige Brennweite f‘: f‘=-R/2=|R|/2. Der bildseitige Brennpunkt der paraxialen Optik und der eine „Brennpunkt“ der Parabel im Sinn der Kegelschnitte fallen also zusammen. -10 0 10 20 30 40 50 60 70 80 90 100 110 r 40 40 30 30 20 20 10 10 0 0 z -10 -10 -20 -20 f’ -30 -30 -40 -40 -10 0 10 20 30 40 50 60 70 80 90 100 110 RAYTRACE Copyright © 2006 University Erlangen-Nuremberg Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+110 Teleskope in der Astronomie Das Newton-Teleskop (ursprünglich von Sir Isaac Newton entwickelt) Sphärischer oder parabolischer Primär-Spiegel (Parabolspiegel keine sphärische Aberration) Planer Fang-Spiegel unter 45o, um das Licht seitlich unter 90o aus dem Tubus heraus auf das Okular zu lenken Quelle: Wikipedia Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+111 Teleskope in der Astronomie Das Cassegrain-Teleskop Konkav-parabolischer Primärspiegel und konvex-hyperbolischer Sekundärspiegel, wobei der optische Brennpunkt des Primärspiegels mit dem einen Kegelschnitt-Brennpunkt des hyperbolischen Sekundärspiegels übereinstimmt, so dass das Licht zum zweiten Kegelschnitt-Brennpunkt des Sekundärspiegels gelenkt wird keine sphärische Aberration, aber lange Brennweite trotz kurzer Baulänge. Licht wird durch ein Loch im Primärspiegel auf das Okular geführt, falls Fokus hinter dem Primärspiegel (für visuelle Beobachtung), oder es befindet sich direkt ein Detektor im Fokus, falls dieser vor dem Primärspiegel liegt. Quelle: Wikipedia Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+112 Teleskope in der Astronomie Einschub: Kombination zweier Spiegel (Primär- und Sekundärspiegel) als Objektiv: Anwendung der paraxialen geometrischen Optik mit „aufgefaltetem Strahlengang“: Brennweiten f‘1 und f‘2 der beiden Spiegel im Abstand d. Matrix M vom Scheitel des ersten zum Scheitel des zweiten Spiegels. d 1 0 1 d 1 0 1 f1' M ' ' 1 / f 2 1 0 1 1 / f1 1 1 1 d f' f' f'f' 2 1 2 1 1 1 1 f1' f 2' d ' ' ' ' f ' ' f ' f1 f 2 f1 f 2 f1 f 2' d d 1 ' f2 d Anmerkung: Die Brennweiten der Spiegel hängen mit den Scheitelkrümmungsradien unabhängig vom Kegelschnitt-Typ gemäß f‘1,2=-R1,2/2 zusammen! Der konische Parameter K bestimmt dann die exakte Lage der KegelschnittBrennpunkte und damit mögliche Aberrationen. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+113 Teleskope in der Astronomie Für unendlich weit entferntes Objekt liegt der Fokuspunkt im Abstand dI vom Sekundärspiegel, wobei gilt: 1 d ' d I 1 ' 1 ' d' ' d d I dd'I f f1 f f f f2 x' 1 d I x 2 1 2 1 M 1 1 d d ' 0 1 ' ' ' ' 1 ' f f f f f 2 1 2 2 1 x Im Fokus muss die Strahlhöhe x‘ unabhängig von der Strahlhöhe x der einfallenden (parallelen) Strahlen sein, so dass also das Matrixelement A der Gesamtmatrix Null ist: 1 1 d d x' Ax B unabhängig von x A 1 ' d I ' ' ' ' 0 f1 f1 f 2 f1 f 2 f d f 2' dI ' f1 f 2' d ' 1 Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+114 Teleskope in der Astronomie Abstand d muss in der Praxis deutlich größer als 0.5*f‘1 sein, damit die Abschattung des Primärspiegels durch den Sekundärspiegel nicht zu groß wird. Beispiel eines Cassegrain-Designs: f‘1=2000 mm, f‘2=-700 mm, d=1500 mm f d f 2' 500 mm - 700 mm 1750 mm dI ' ' f1 f 2 d 200 mm ' 1 2000 mm - 700 mm f1' f 2' f ' ' 7000 mm ' f1 f 2 d 200 mm d dI Für dieses Cassegrain-Teleskop liegt der optische Fokus also nur 250 mm hinter dem Primärspiegel bzw. die Baulänge vom Sekundärspiegel (der am nächsten zum Objekt ist) zum Fokus ist nur dI=1750 mm, während die effektive Brennweite f‘=7000 mm beträgt! Kompakter Bau Hätte man nur einen einzigen Spiegel, so müsste die Baulänge gleich f‘ sein. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+115 Teleskope in der Astronomie • Konische Konstante des Primärspiegels (=Parabolspiegel) ist K=-1. Konische Konstante des Sekundärspiegels (=hyperbolischer Spiegel) ergibt sich daraus, dass der erste Brennpunkt des Hyperboloids mit dem Brennpunkt des Primärspiegels übereinstimmen muss. e=f‘1-d=500 mm • Krümmungsradius R des Sekundärspiegels ergibt sich aus f‘2: R=-2f‘2=1400 mm e R R 1400 14 1 K e 500 5 1 K Da –K>1 für Hyperboloid, kann nur der Term mit dem „+“-Zeichen eine Lösung ergeben: 1 K 14 5 K R 1400 mm -1750 mm d I 1 9 / 5 1 K Geometrische und Technische Optik e dI 9 81 K 3.24 5 25 Zur Überprüfung: Die zweite Lösung ergibt e d Negatives Vorzeichen deutet an, dass zweiter Brennpunkt auf anderer Seite des Spiegels als erster Brennpunkt ist. Institut für Optik, Information und N. Lindlein Photonik 126+116 Teleskope in der Astronomie Ray tracing Simulation des Beispiels: D=0.5 m, f‘=7 m, =0.5 µm Distances in mm, horizontal z-axis, vertical x-axis -1500 -1000 -500 Distances in mm, horizontal z-axis, vertical x-axis 0 -1500 600 600 400 400 200 Maßstabsgerecht 200 0 -1000 -500 0 250 250 200 200 150 150 100 100 50 50 0 0 0 -50 -200 -200 -400 -400 -600 Zoom -600 -1500 -1000 -500 -100 -150 -150 -200 -200 -250 -250 -1500 0 10-8 µm! D.h. in Praxis beugungsbegrenzt -50 -100 Spotdiagramme von Objektpunkten Auf Achse -1000 -500 0 20 µm 0.1o off-axis Zum Vergleich: beugungsbegrenzter Spot hat Durchmesser 2.44f‘/D=17 µm Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+117 Teleskope in der Astronomie Das Schmidt-Cassegrain-Teleskop Am Eingang wird eine asphärische Phasenplatte (Glasplatte) zur Korrektur der sphärischen Aberration des sphärischen Primär-Spiegels angebracht. Ein konvexer (hyperbolischer) Sekundärspiegel lenkt dann das Licht durch ein Loch im Primärspiegel auf das Okular bzw. Detektor. Die Schmidt-Kamera Nur für photographische Zwecke ist die SchmidtKamera geeignet, bei der eine asphärische Glasplatte mit Blende im Krümmungsmittelpunkt eines sphärischen Spiegels dessen sphärische Aberration korrigiert. Der Detektor muss sich im Tubus befinden, wobei Bildfeldwölbung auftritt. Durch das kugelsymmetrische Design sind Coma und Astigmatismus weitgehend korrigiert! Geometrische und Technische Optik Quelle: Wikipedia Institut für Optik, Information und N. Lindlein Photonik 126+118 Teleskope in der Astronomie Das Ritchey-Chrétien-Cassegrain-Teleskop Kombination zweier spezieller hyperbolischer Spiegel, die eine komafreie Abbildung ermöglichen. Bildfeld ist allerdings nach wie vor gekrümmt und muss anderweitig korrigiert werden. Quelle: Wikipedia Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+119 Teleskope in der Astronomie (Winkel-)Auflösungsvermögen eines (Spiegel-)Teleskops Wie schon mehrfach erwähnt wurde, begrenzt die Beugung die Auflösung eines Teleskops, vorausgesetzt das Teleskop hat keine Aberrationen. Bei einem Durchmesser D des Primärspiegels (=Eintrittspupille) und der Wellenlänge beträgt der Winkel zwischen zwei punktförmigen, (unendlich) weit entfernten Objekten, die gerade noch aufgelöst werden können: k D Die Konstante k kann in der Praxis gleich eins gesetzt werden. Für eine Kreisapertur (ohne Obskuration) gilt k=1.22. Bei einer Ringapertur wie beim Newton- oder Cassegrain-Teleskop ist k leicht verschieden davon, je nachdem wie groß der innere Ring ist. Um eine aberrationsfreie Abbildung zu erhalten, müssen bei erdgebundenen Teleskopen aber Luftturbulenzen und Verbiegungen des Spiegels durch das Eigengewicht korrigiert werden. Adaptive und aktive Optik nötig (z.B. beim VLT) Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+120 Teleskope in der Astronomie Zusammenhang Winkel-Auflösungsvermögen, Spiegeldurchmesser, Brennweite eines (Spiegel-)Teleskops Große Brennweite f‘ des Spiegelsystems bedeutet auch eine große laterale Vergrößerung: x f ' (Objekt mit Winkelgröße , laterale Größe x des Objekts auf dem Detektor) Durchmesser D des Primärspiegels (=Eintrittspupille), Wellenlänge Winkel zwischen zwei punktförmigen, (unendlich) weit entfernten Objekten, die gerade noch aufgelöst werden können, und entsprechende Größe x auf Detektor: k D D x f ' f ' D Maximal sinnvolle laterale Vergrößerung ergibt sich daraus, dass die Pixel des Detektors einen Abstand xPixel von ca. 0.5*x haben (damit Intensitätsabnahme zwischen zwei auflösbaren Objektpunkten noch messbar ist): 2xPixel x f ' Geometrische und Technische Optik D f ' 2 D xPixel Institut für Optik, Information und N. Lindlein Photonik 126+121 Teleskope in der Astronomie Für typischen CCD-Detektor mit hoher Intensitätsauflösung ( große Pixel), wie in Astronomie üblich, ist xPixel=10 µm bis xPixel=25 µm. Die maximal sinnvolle Blendenzahl f# ergibt sich dann in etwa zu (=0.5 µm): f ' 2 D xPixel f # x f' 2 Pixel 40 100 D In der Praxis wählt man die Blendenzahl meist etwas kleiner (ca. 13-50), da die Auflösung des Teleskops durch andere Faktoren etwas schlechter ist bzw. die Wellenlänge größer (IR), etc. Auch die nötige kompakte Bauweise der Riesenteleskope begrenzt die Brennweite. Feldwinkel Feld: Der Durchmesser xCCD des Detektors (= Anzahl NCCD der Pixel pro Zeile * xPixel) bestimmt mit der Brennweite f‘ den Feldwinkel: Feld xCCD N CCD xPixel f' f' Geometrische und Technische Optik z.B. f‘=100 m, NCCD=8000, xPixel=20 µm Feld=0.1o Institut für Optik, Information und N. Lindlein Photonik 126+122 Teleskope in der Astronomie Astronomische Kameras mit großen Feldwinkeln bis ca. 12o müssen also deutlich kleinere Brennweiten haben, da die Detektoren nicht viel größer werden können. Die resultierende Winkelauflösung der Kameras ist nicht so hoch wie sie laut der Beugungsbegrenzung sein könnte. Beispiel: Kepler Teleskop = Schmidt-Kamera zur Beobachtung von Exo-Planeten, Spiegel-Durchmesser ca. 1 m, Brennweite auch ca. 1 m, 42 CCD-Chips mit je 2200x1024 Pixel (Pixel-Größe ca. 25 µm) Quelle: NASA Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+123 Teleskope in der Astronomie Auflösungsbegrenzung durch Luftturbulenzen Durch unterschiedliche Brechzahlen (wegen unterschiedlichem lokalen Luftdruck) auf dem Weg des Lichts durch die untersten 15 km der Atmosphäre (Troposphäre) sind die optischen Weglängen verschiedener Strahlen in der Spiegelebene unterschiedlich Winkelauflösung eines Teleskops am Erdboden ist auf ca. 1 Bogensekunde begrenzt! k D 1' ' 5 10 6 k D 500 nm k 1 100 mm Dies wäre der Durchmesser eines einfachen Hobby-Teleskops und professionelle Teleskope für die Astronomie mit Spiegeldurchmessern von mehr als D=5 m wären von der Winkelauflösung um ca. einen Faktor 50 schlechter als durch die Beugung vorgegeben! Moderne Teleskope werden auf hohen Bergen installiert wegen der dünneren Atmosphäre. Weitere Korrektur durch deformierbare Spiegel nötig. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+124 Teleskope in der Astronomie Adaptive Optik zur Korrektur von atmosphärischen Turbulenzen Korrektur der Luftturbulenzen durch deformierbaren Spiegel. Regelgeschwindigkeit muss bei ca. 100 Hz liegen, um die atmosphärischen Schwankungen auszugleichen. Typischerweise wird der kleinere Sekundärspiegel oder ein weiterer (ebener) Spiegel deformiert. Messung der Wellenaberrationen mit ShackHartmann-Sensor meist anhand eines fernen Leitsterns (=ideale Punktlichtquelle). Aktive Optik funktioniert nach gleichem Prinzip, korrigiert aber nur Verformungen des Spiegels aufgrund der Bewegung. Die Messung erfolgt deshalb auch nur ca. jede Minute. Geometrische und Technische Optik Quelle: Wikipedia Institut für Optik, Information und N. Lindlein Photonik 126+125 Teleskope in der Astronomie Shack-Hartmann-Sensor zur Messung von WellenfrontDeformationen Mikrolinsenarray mit Brennweite f‘ vor einem Detektor (CCD-Kamera) • Laterale Spotauslenkungen hängen von lokaler Steigung der Wellenfront ab • Interpretation als lokale Ableitungen der Wellenfront (W: optische Weglänge): W x x f' W y y f' y deformierte Wellenfront lokale Koordinaten x lokale Opt. Achsen Integration liefert die Wellenfront Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+126 Das Mikroskop Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+127 Das Mikroskop Um kleine nahe Objekte vergrößert abzubilden, gibt es mehrere Möglichkeiten: • Die Lupe • Das visuelle Mikroskop zum direkten Betrachten mit dem Auge • Das Inspektions-Mikroskop mit elektronischem Detektor • Weitere Möglichkeiten: • Laser-Scanning-Mikroskop oder konfokales Mikroskop: in beiden Fällen wird ein Objekt Punkt für Punkt abgerastert • Dunkelfeld-, Polarisations- oder Phasenkontrast-Mikroskop: spezielle wellenoptische Eigenschaften werden ausgenutzt Je nach Beleuchtungsart unterscheidet man auch Auflicht- und Durchlicht-Mikroskope Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+128 Das Mikroskop Die Lupe: Die Größe eines Objektes auf unserer Netzhaut hängt vom Sehwinkel O ab, unter dem das Objekt erscheint. dO,2 xO jO,1 Hauptebene des Auges xO jO,2 Auge dO,1 Um so näher das Objekt am Auge ist, desto größer erscheint es. Aber das Auge hat eine minimale Entfernung, auf die es scharf stellen kann. Zum entspannten Betrachten ist dies die sogenannte deutliche Sehweite dS=25 cm Eine Sammellinse direkt vor dem Auge, die Lupe, kann ein vergrößertes virtuelles Bild im Abstand |dI|=dS vor dem Auge erzeugen. Anmerkung: Man kann eine Lupe auch so benutzen, dass sie nicht direkt vor dem Auge ist. Diesen Fall betrachten wir hier aber nicht. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+129 Das Mikroskop Da das menschliche Auge nur in Luft scharfe Bilder liefert, gilt im Bildraum der Lupe n‘=1. Abbildungsgleichung für Brechzahl n zwischen Objekt und Lupe (wenn auch meist n=1): 1 n 1 d I dO f' f‘: Brennweite der Lupe Lupe xI dI jI=jO xO dO Auge F Objekt Grafik für n=n‘ Wegen Vorzeichen-Definition sind sowohl dO als auch dI = -dS negativ. Für den lateralen Abbildungsmaßstab gilt: d x d d d I I I n I 1 I 1 S xO O d O dO f' f' n ' 1 wobei n' I nO I n (paraxialer Fall) O Beispiel: Lupe mit f‘=5 cm =1+25/5=6 Anm.: In der Praxis ist eine gute Lupe ein achromatisches mehrlinsiges System. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+130 Das Mikroskop Einsatzgrenze der Lupe: Für starke Vergrößerung muss die Brennweite f‘ sehr klein sein und deshalb das Objekt sehr nahe an die Lupe und damit auch ans Auge gebracht werden. Vergrößerung der Lupe ist begrenzt. Ausweg: zweistufige Abbildung im Mikroskop zur visuellen Betrachtung: • Mikro-Objektiv erzeugt reelles vergrößertes Zwischenbild des Objekts mit Abbildungsmaßstab 1<0 und |1|>>1 (in Praxis |1| zwischen etwa 5 und 100). • Dieses Bild wird mit einer Lupe (hier genannt: Okular) nochmals um den Faktor 2>1 (|2| zwischen etwa 5 und 20) vergrößert, so dass ein stark vergrößertes virtuelles Bild im Abstand der deutlichen Sehweite vor dem Auge erzeugt wird. Der resultierende laterale Abbildungsmaßstab ist das Produkt der beiden Abbildungsmaßstäbe 1 und 2: Mikro-Objektiv Okular Reelles Zwischenbild Objekt F1 F2F’1 1 2 mit 0 1 Virtuelles Bild Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+131 Das Mikroskop Anmerkungen: • Das Mikro-Objektiv muss achromatisch sein, eine hohe numerische Apertur und ein großes aberrationsfreies Feld haben. Kompliziertes System aus vielen Linsen nötig. Sinus-Bedingung muss erfüllt sein Coma korrigiert. • Oftmals sind moderne Mikro-Objektive auf „unendlich korrigiert“, d.h. das Objekt befindet sich exakt in der vorderen Brennebene und hinter dem Objektiv entsteht für jeden Objektpunkt eine (geneigte) ebene Welle. Das reelle Zwischenbild wird mit einer zusätzlichen, sogenannten Tubus-Linse erzeugt, deren Brennweite gleich der Tubuslänge (oft 160 mm) ist. Vorteil dieser Konfiguration ist, dass der Abstand zwischen Mikro-Objektiv und Tubuslinse weitgehend beliebig sein kann und dort nur ebene Wellen vorhanden sind, die beim Durchgang durch Planplatten, wie z.B. in einem Strahlteiler, keine zusätzlichen Aberrationen erzeugen. • Bei biologischen Objekten befindet sich zwischen Objekt und Mikro-Objektiv oft ein Deckglas. Die Aberrationen beim Durchgang der Kugelwelle vom Objekt durch das Deckglas müssen dann im Design des Mikro-Objektivs korrigiert werden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+132 Das Mikroskop Mikroskop mit Objektiv, das für endliche oder unendliche Entfernung des Bildes korrigiert ist: Intermediate Image Distance Achtung: Bild des Okulars ist natürlich virtuell mit Bildlage vor dem Okular bzw. im Unendlichen. Quelle: http://www.microscopyu.com/articles/optics/images/infinityoptics/infinityfigure2.jpg Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+133 Das Mikroskop Auflösungsgrenze des Mikroskops (für inkohärentes Licht): Zwei Objektpunkte mit lateralem Abstand x können, wenn sie inkohärent zueinander strahlen, gerade dann noch aufgelöst werden, wenn gilt: NA k x n sin 1 0.9 x k 0.7 0.6 0.5 0.4 Intensity (normalized) 0.3 0.2 0.1 0 n: Brechzahl zwischen Objekt und Mikro-Objektiv : (halber) Aperturwinkel des Mikro-Objektivs k: Konstante, die bei einer Kreisapertur normalerweise 0.61 ist, die aber je nach Beleuchtung und Detektor (z.B. bei Nichtlinearität oder Schwellenempfindlichkeit) auch etwas kleiner oder größer sein kann. 0.8 : Wellenlänge im Vakuum -0.01 -0.006 -0.002 0 0.002 0.006 0.01 x-axis (mm) Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+134 Das Mikroskop Abbe‘sche Theorie des Mikroskops (für kohärentes Licht): Alternative Betrachtungsweise zur Auflösungsgrenze, indem ein periodisches Objekt (Linien-Gitter) der Periodenlänge p betrachtet und mit einer ebenen Welle beleuchtet wird. m=1 j’1 m=0 Damit das Gitter gerade noch abgebildet wird, müssen mindestens die 0. Beugungsordnung und eine der ersten Beugungsordnungen vom Objektiv übertragen werden. p Bei achsenparalleler Einstrahlung (oberes Bild) muss dann für den Beugungswinkel ‘1 in erster Beugungsordnung gelten (: Aperturwinkel des Mikro-Objektivs, n: Brechzahl vor Objektiv): n sin '1 p n sin p n sin NA Bei schräger Beleuchtung (unteres Bild) kann man das gleiche Gitter schon bei kleinerem Aperturwinkel gerade noch abbilden. Geometrische und Technische Optik m=-1 m=1 j’1 m=0 j p m=-1 Institut für Optik, Information und N. Lindlein Photonik 126+135 Das Mikroskop Sinnvolle maximale Vergrößerung eines visuellen Mikroskops: Um die für ein visuelles Mikroskop sinnvolle maximale Vergrößerung || zu berechnen, muss man zuerst die Auflösung des Auges kennen. Bei der Besprechung des menschlichen Auges hatten wir gesehen, dass dieses unter optimalen Bedingungen zwei Objekte mit Sehwinkel-Abstand von =30‘‘ noch unterscheiden kann. Unter normalen Bedingungen und „entspanntem“ Sehen sollte man also zwei Objekte im Abstand der deutlichen Sehweite mit =2‘ noch gut unterscheiden können. Der laterale Abstand xAuge der auflösbaren Punkte ist dann: x Auge d S 250 mm 2 180 60 0.15 mm Der Abstand x zweier Punkte des Objekts unter dem Mikroskop, die bedingt durch Beugung gerade noch aufgelöst werden können, sollte also auf die Größe xAuge vergrößert werden, so dass für den Abbildungsmaßstab || gilt: x Auge x x Auge NA 500 nm k NA 1, k 0.61 Geometrische und Technische Optik 500 Stärkere Vergrößerungen als ca. 500-1000 machen also in der Praxis keinen Sinn! Institut für Optik, Information und N. Lindlein Photonik 126+136 Das Mikroskop Das Inspektions-Mikroskop mit elektronischem Detektor: In der Praxis sieht man heutzutage oft nicht direkt durch ein Mikroskop, sondern nimmt das Bild mit einem CCD-Chip auf und schaut es auf einem Bildschirm an. Auf dem CCD-Chip muss ein reelles Bild vorhanden sein. Das Okular entfällt. Sinnvolle maximale Vergrößerung || liegt dann vor, wenn der Intensitätsabfall zwischen zwei gerade noch auflösbaren Objektpunkten auf dem CCD-Chip sichtbar ist. Für Pixelabstand d muss gelten: d x 2d NA k 2 2 NA k Abstand d der CCD-Pixel typischerweise 5 µm d 20 µm (bzw. d=25 µm für lichtschwache astronomische Anwendungen). Beim Mikroskop eher 5 µm d 10 µm. Für sichtbares Licht (=500 nm), Objekt in Luft (d.h. n=1) und sin=1 (maximaler Wert) folgt dann für k=0.61 und Pixelabstand d=10 µm: ||=66 Das reelle Bild kann mit einem hochaperturigen Mikro-Objektiv erzeugt werden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+137 Das Mikroskop UV-Mikroskope mit Wasser-Immersion: Höchste Auflösung mit „Licht“-Mikroskop Reduktion der Wellenlänge und Erhöhung der numerischen Apertur durch Immersionsflüssigkeit zwischen Objekt und Mikro-Objektiv. Systeme zur Inspektion von Masken für ICs: =248 nm und NA1.25 (Brechzahl Wasser im UV n1.38). Damit erhält man (für k=0.61): x=120 nm Möchte man den Intensitätsabfall zwischen zwei gerade noch auflösbaren Objektpunkten also auf einem CCD-Pixel (d=12 µm) detektieren, muss die Vergrößerung betragen: d 2 x 200 Quelle: Leica, http://www.dgao-proceedings.de/download/106/106_a28.pdf Es gibt mittlerweile Mikro-Objektive mit direkter 200-facher Vergrößerung. Auch eine zweistufige reelle Abbildung ist möglich, wobei das zweite Abbildungssystem nur eine sehr geringe numerische Apertur haben muss, da diese ja durch die erste Abbildung mit Abbildungsmaßstab 1 stark verringert wird: NABild=NAObjekt/|| Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+138 Das Mikroskop Verschiedene Arten der MikroskopBeleuchtung: Strahlengänge im Mikroskop einschließlich Beleuchtungssystem (Kondensor): • Feldblende des Kondensors bestimmt die Größe des beleuchteten Objektfelds/Prüflings • Aperturblende des Kondensors bestimmt die Winkel, unter denen das Objekt beleuchtet wird Quelle: http://web.uvic.ca/ail/techniques/ scope light path.jpg Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+139 Das Mikroskop Hellfeld-Beleuchtung: • Probe wird im Durchlicht oder Auflicht aus verschiedenen Richtungen beleuchtet. • Ungestreutes Hintergrundlicht und gestreutes Licht gehen durchs Objektiv Feld um Probe ist hell. • Bildgebung erfolgt durch Absorption der Probe. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+140 Das Mikroskop Dunkelfeld-Beleuchtung: • Probe wird im Durchlicht oder Auflicht nur aus Richtungen mit großen Winkeln beleuchtet. • Ungestreutes Hintergrundlicht wird von Objektiv nicht erfasst (zu große Winkel), an der Probe gestreutes Licht geht durchs Objektiv Feld um Probe ist dunkel. • Bildgebung erfolgt durch an der Probe gestreutes Licht. Quelle: Wikipedia Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+141 Das Mikroskop Kreuzpolarisations-Beleuchtung: • Probe wird mit Hilfe eines Polarisators mit linear polarisiertem Licht beleuchtet. Das Licht hinter der Probe geht durch einen zweiten, aber gekreuzten Polarisator (d.h. Polarisationsachse um 90 Grad gedreht). • Nur Licht, dessen Polarisationszustand durch die Probe verändert wurde, wird von zweitem Polarisator durchgelassen Feld um die Probe ist wiederum dunkel. • Bildgebung erfolgt durch die Polarisationseigenschaften der Probe (Rotation der Polarisationsrichtung). Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+142 Das Mikroskop Phasenkontrast Mikroskop (Zernike’s Phasenkontrast-Methode): • Probe wird mit ringförmigem Winkelspektrum ebener Wellen beleuchtet, die alle den gleichen Winkel relativ zur optischen Achse haben. • Ungestreutes Licht formt in der hinteren Brennebene des Objektivs einen Ring. Die Phase dieses Lichts wird um /2 (90o) verschoben, indem ein schmaler ringförmiger Bereich mit Tiefe /(4(nglass-1)) in eine Glasplatte geätzt wird. Das an der Probe gestreute Licht wird nicht zusätzlich in der Phase geschoben. • Durch Interferenz zwischen dem an der Probe gestreuten und dem phasenverschobenen ungestreuten Licht werden Phaseninformationen (optische Weglängenänderungen) der Probe als Intensitätsschwankungen sichtbar. In einem normalen Mikroskop sind reine Phasenobjekte dagegen unsichtbar. • Bildgebung erfolgt durch die Phase der Probe. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+143 Das Mikroskop Verschiedene Durchleuchtungsmethoden (Probe: Toilettenpapier, 1.6 µm/Pixel): HellfeldBeleuchtung DunkelfeldBeleuchtung Quelle: Wikipedia KreuzpolarisatorBeleuchtung Geometrische und Technische Optik Phasenkontrast Mikroskopie Institut für Optik, Information und N. Lindlein Photonik 126+144 Das Mikroskop Das konfokale Mikroskop: • Im Gegensatz zu allen bisherigen Arten von Mikroskopen, bei denen ein Bild der Probe parallel auf einmal geformt wurde, beleuchtet das konfokale Mikroskop nur einen punktförmigen Bereich der Probe zu einem Zeitpunkt. • Bild der Probe erfolgt durch Abtastung der Probe (in 3 Dimensionen). • Spezialität des konfokalen Mikroskops ist die hohe Tiefenauflösung, die von einer punktförmigen Blende vor dem Detektor stammt. Nur wenn der betrachtete Punkt der Probe im Fokus der Beleuchtung ist, kann das an der Probe reflektierte Licht die Blende vor dem Detektor ungehindert passieren. Das konfokale Fluoreszenzmikroskop: Nur von der Probe mittels Fluoreszenz emittiertes Licht (d.h. andere Wellenlänge als beleuchtendes Licht) wird detektiert. Resultierende Punktbildfunktion (PSF) ist das Produkt der Beleuchtungs-PSF und der Abbildungs-PSF höhere Tiefenauflösung Quelle: Wikipedia und leicht höhere laterale Auflösung. Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+145 Das Mikroskop PSF normales Mikroskop Laterale Auflösung ca. 0.61/NA Laterale PSF Axiale PSF PSF konfokales Mikroskop (=PSF2) Vergleich der PSFs eines normalen und eines konfokalen Mikroskops: Laterale Auflösung ca. 0.4/NA NA=0.5 =0.5 µm Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+146 Das Mikroskop Konfokales Mikroskop mit Nipkow-Scheibe: Durch Verwendung einer Nipkow-Scheibe mit vielen spiralförmig angeordneten Lochblenden können auch viele Punkte der Probe auf einmal beleuchtet und detektiert werden. Randbedingung: alle Lochblenden müssen soweit voneinander entfernt sein, dass ihre Punktbildfunktionen im Bild nicht überlappen. Durch Rotation der Nipkow-Scheibe werden alle Punkte der Probe abgetastet. Während für ein punktförmig abtastendes Mikroskop ein Single-Pixel-Detektor verwendet werden kann (z.B. Photomultiplier), erfordert das konfokale Mikroskop mit Nipkow-Scheibe einen ArrayDetektor (z.B. CCD). Quelle: http://images.pennnet.com/articles/lfw/thm/th_0505lf09f3.gif Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+147 Das Mikroskop Vergleich Teleskop und Mikroskop: Teleskop Mikroskop Zweck Soll (unendlich) weit entfernte Soll nahe sehr kleine Objekte (meist sehr große) Objekte vergrößert abbilden. vergrößert abbilden. Prinzip Winkelvergrößerung =‘/ Auflösung Winkelauflösung kT D Laterale Vergrößerung =x‘/x Ortsauflösung kT=1.22 für Kreisapertur x k M Zusammenhang zwischen den Größen: sin NA kM n sin kM=0.61 für Kreisapertur D und x f ' kT 2k M 2f' : Winkel, unter dem das Objekt erscheint, ‘: Winkel, unter dem das Bild erscheint, x, x‘: laterale Objekt- bzw. Bildgröße, : Wellenlänge im Vakuum, D: Aperturdurchmesser, n: Brechzahl zwischen Objekt und Objektiv, : (halber) Aperturwinkel, f‘: Brennweite des Objektivs Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+148 Anwendung optischer Methoden in der Astronomie: Detektion erdähnlicher Planeten um andere Sterne Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+149 Detektion erdähnlicher Planeten Im Folgenden sollen Verfahren zum Auffinden erdähnlicher Planeten um andere Sterne diskutiert werden. Was hat dies mit technischer Optik zu tun? Letztendlich stammt die gesamte Information, die wir in der Astronomie von fernen Sternen und Sternsystemen bisher haben, von elektromagnetischer Strahlung (Detektionsverfahren für Gravitationswellen und Neutrinos sind erst in der Entwicklung und würden bei der Suche nach Exoplaneten kaum helfen). Davon wiederum hat das Spektrum vom fernen Infrarot bis zum nahen Ultraviolett, in dem optische Methoden zum Einsatz kommen, den wichtigsten Anteil. Verfahren der technischen Optik in Kombination mit anderen physikalischen Verfahren kommen zum Einsatz. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+150 Detektion erdähnlicher Planeten Methode 1: Periodische Doppler-Verschiebung der Spektrallinien des Sterns aufgrund der Rotation um den gemeinsamen Schwerpunkt (Radialgeschwindigkeits-Methode) Mit dieser Methode wurden schon mehrere Riesenplaneten mit sehr kleinen Bahnradien nachgewiesen. Momentane „Standardmethode“. Könnte mit diesem Verfahren auch ein erdähnlicher Planet in einem unserem Sonnensystem ähnlichen Planetensystem nachgewiesen werden? Als Modellsystem betrachten wir für alle Methoden unser eigenes Sonnensystem und unsere Erde und versuchen abzuschätzen, ob wir die Erde aus vielen Lichtjahren Entfernung nachweisen könnten. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+151 Detektion erdähnlicher Planeten Verwendete Größen: Erdmasse mE=5.974.1024 kg, Sonnenmasse MS=1.989.1030 kg, Abstand Erde-Sonne r=1 AE=149.6.106 km, Abstand Sonne vom gemeinsamen Schwerpunkt rS, Abstand Erde vom gemeinsamen Schwerpunkt rE. Kreisbahn wird angenommen! r Schwerpunktsbedingung: mE rE M S rS rS Sonne rE Schwerpunkt Erde r rE rS r rE r mE M mE MS rE S rE rE r MS MS M S mE MS M mE mE rS rS S rS rS r mE mE M S mE Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+152 Detektion erdähnlicher Planeten Zentrifugalkraft = Gravitationskraft v 2E GmE M S mE M S mE 2 GmE M S vE vE M S mE 2 2 rE r MSr r G M S mE r v 2S GmE M S M S M S mE 2 GmE M S vS v S mE MS 2 2 rS r mE r r G M S mE r vE: Bahngeschwindigkeit des Planeten um Schwerpunkt; vS: Bahngeschwindigkeit des Sterns um Schwerpunkt Gravitationskonstante G=6.67.10-11 m3.kg-1.s-2 Umlaufzeit T (selbstverständlich für Stern und Planet gleich): MS 2 2 v E E rE rE r MS T T M S mE G M S mE r r3 T 2 365.3 Tage (für Erde) G M S m E Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+153 Detektion erdähnlicher Planeten Optischer Dopplereffekt: v2 1 2 c 0 v 1 cos c 0 v / c 1 1 v cos c v 0 1 cos c v / c 1 : Frequenz des dopplerverschobenen Lichts, 0: Frequenz bei ruhendem Objekt, v: Betrag der Relativ-Geschwindigkeit zwischen Objekt und Beobachter, c: Lichtgeschwindigkeit, : Winkel zwischen Beobachtungsrichtung und Bewegungsrichtung des Objekts: =0 Objekt entfernt sich (Rotverschiebung), = Objekt nähert sich (Blauverschiebung) Doppler-Verschiebung ist also maximal, wenn die Bahnebene des Systems parallel zur Beobachtungsrichtung ist. Die Stärke nimmt aber nur Kosinus-förmig ab, wenn dies nicht der Fall ist. In ersterem Fall ist /0 während eines vollen Umlaufs: v 2 0 c Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+154 Detektion erdähnlicher Planeten Abschätzung Doppler-Verschiebung in unserem Sonnensystem: Bahngeschwindigkeit vS um Schwerpunkt bzw. maximale Doppler-Verschiebung der Sonne (Bahnebene || Beobachtungsrichtung) aufgrund des Einflusses von Jupiter: mJ=1.899.1027 kg, MS=1.989.1030 kg, rJ=5.204 AE, c=2.998.108 m s-1 v S mJ vS G m 12.5 2 8.3 10 8 M S mJ rJ s c 0 Anschaulicher Vergleich: 100 m Weltklasse-Sprinter erreicht in etwa diese Geschwindigkeit. Man müsste also die Spektralverschiebung einer Spektrallampe messen können, die er beim Sprint mit sich trägt. Einfluss der Erde auf die Sonne: mE=5.974.1024 kg, rE=1 AE v S mE Bisher minimal messbare Geschwindigkeit ca. 1 m/s Zu klein für Messung! vS G mE m 0.089 2 2 M S mE rE 0 c c s Geometrische und Technische Optik G 6 10 10 M S mE rE Institut für Optik, Information und N. Lindlein Photonik 126+155 Detektion erdähnlicher Planeten Methode 2: Verdunkelung des Sterns aufgrund der Passage eines Planeten zwischen Stern und Beobachter (Transit-Methode) Mit dieser Methode wurden auch schon einige Riesenplaneten nachgewiesen. Voraussetzung: Die Bahnebene des Planeten muss fast parallel zur Beobachtungsrichtung sein. Die Spitze des BahnebenenNormalenvektors muss also auf der Einheitskugel auf einem Ring senkrecht zur Beobachtungsrichtung liegen, dessen Winkeldicke durch das Verhältnis DS/r gegeben ist (DS: Durchmesser des Sterns (=Sonne), r: Bahnradius des Planeten (=Erde)). Wahrscheinlichkeit W, dass dies der Fall ist: 2DS / r DS 1.39 106 km W 0.005 0.5% 6 4 2r 2 149.6 10 km Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+156 Detektion erdähnlicher Planeten Relative Reduktion der Helligkeit I/I0 des Sterns beim Durchzug des Planeten hängt vom Flächenverhältnis beider Himmelskörper ab (Durchmesser Stern DS, Durchmesser Planet DE), ist aber unabhängig vom Abstand zum Beobachter: 2 DE2 10 2 1% (für Jupiter mit DJ 1.38 105 km) I DE / 2 2 4 2 I 0 DS / 2 DS 10 0.01% (für Erde mit DE 1.27 10 4 km) Dauer t des Vorbeizugs des Planeten am Stern bei zentralem Vorbeizug, d.h. Bahnebene exakt parallel zur Beobachtungsrichtung (T: Umlaufdauer des Planeten um den Stern, r: Bahnradius): DS 1.39 106 km t T 365 24 h 13 h (für Erde) 6 2r 2 149.6 10 km Natürliche Schwankung der Helligkeit der Sonne 0.1% Helligkeitsreduktion bei Durchzug eines erdähnlichen Planeten kaum vom natürlichen „Rauschen“ unterscheidbar. Beobachtung müsste auf jeden Fall ständig und über mehrere Umläufe/Jahre erfolgen, damit ein periodisches Signal aus dem Rauschen gefiltert werden könnte! Nur vom Weltall aus möglich wegen Helligkeitsschwankung durch Atmosphäre! Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+157 Detektion erdähnlicher Planeten Methode 3: Direkte Beobachtung des Planeten. Winkelauflösungsvermögen eines Teleskops mit Spiegeldurchmesser D bei der Wellenlänge : D Bei Beobachtung aus d=10 Lichtjahren Entfernung und =500 nm müsste dann für den Spiegeldurchmesser gelten (r: Bahnradius): d r 10 365 24 3600 3 108 m 6 D 0 . 5 10 m 9 D d r 149.6 10 m 10 9.46 1015 m 6 0 . 5 10 m 0.32 m 9 149.6 10 m Hubble-Weltraum-Teleskop mit D=2.4 m wäre also ausreichend? ACHTUNG!!! Gleichung für Auflösungsvermögen gilt nur für zwei gleich helle Punkte! Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+158 Detektion erdähnlicher Planeten Exkurs in Wellenoptik: Intensitätsverteilung I() (Airy-Verteilung) des Bildes eines -entfernten Objektes in Brennebene eines Teleskops mit kreisförmiger Apertur (Durchmesser D, Brennweite f‘, : radiale Koordinate in Brennebene, Wellenlänge Intensität der einfallenden ebenen Welle I0): D 2 J 1 ˆ D D I ˆ I 0 mit ˆ f' 4 f ' ˆ : entsprechende Winkel-Koordinate 2 2 Erste Nullstelle der Airy-Verteilung bei: ˆ 1.22 1.22 D D Asymptotisches Verhalten für ̂ : I ˆ ˆ 8 cos 2 ˆ 3 / 4 I 0 ˆ 3 Geometrische und Technische Optik ^)]2 [2J1(pr ^)/(pr 2 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 -3 -2 -1 0 1 2 ^ r Institut für Optik, Information und N. Lindlein Photonik 126+159 3 Detektion erdähnlicher Planeten Auflösungsvermögen für zwei Punkte nach Rayleigh: Maximum der Intensität des einen Punktes fällt mit dem ersten Minimum der Intensität des zweiten Punktes zusammen. Hierbei werden aber zwei gleich helle Punkte angenommen! D 1 0.9 D 0.8 Geometrische und Technische Optik 0.6 0.5 0.4 0.3 0.2 0.1 0 Im Fall eines Sterns und eines Planeten sind die Intensitäten aber extrem unterschiedlich, so dass das IntensitätsMaximum des Planetenbildes selbst von weit außen liegenden Nebenmaxima höherer Ordnung des Sternbildes überstrahlt wird. Intensity (normalized) 0.7 1.22 -0.01 -0.006 -0.002 0 0.002 0.006 0.01 x-axis (mm) Institut für Optik, Information und N. Lindlein Photonik 126+160 Detektion erdähnlicher Planeten Überblick über nötige Spiegeldurchmesser bzw. erreichbare Auflösung bei Beobachtung einiger Objekte in Astronomie oder Alltag: Erdbeobachtung mit Satellit: Entfernung ca. d=300 km, Spiegeldurchmesser ca. D=3 m, Wellenlänge =0.5 µm Auflösung x (in Praxis wegen Einfluss der Atmosphäre geringer): x d d 5 cm Autonummern bzw. Gesichter nicht erkennbar! D Beobachtung des Mondes von der Erde aus: Entfernung d=384 000 km, Spiegeldurchmesser zur Zeit maximal D=10 m, Wellenlänge =0.5 µm Auflösung x (in Praxis wegen Einfluss der Atmosphäre geringer): Überreste von Apollo-Mondlandungen (x<5 m) x d d 20 m nicht sichtbar! D Sonnennächster Stern Alpha Centauri A: d=4.34 Lichtjahre=4.11.1016 m, =0.5 µm, Durchmesser des Sterns D centauri1.22.DS=1.7.109 m nötiger Spiegel-Ø d 12 m Selbst sonnennächster Stern ist heutzutage noch nicht D D ,centauri auflösbar, d.h. alle Sterne sind punktförmige Lichtquellen Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+161 Detektion erdähnlicher Planeten Intensitätsverhältnis Planeten- zu Sternbild im VIS am Beispiel Erde: Gesamte von der Sonne emittierte Strahlungsleistung PS: Solarkonstante E0=1367 W/m2 * Kugeloberfläche mit Erdbahnradius rE=1 AE PS 4 rE2 E0 3.8 10 26 W Gesamte von der Erde direkt rückgestreute Strahlungsleistung PE (d.h. ohne Änderung der Spektralzusammensetzung): Solarkonstante E0=1367 W/m2 * Scheibe mit Erddurchmesser DE=12700 km * Albedo =0.367 der Erde (Verhältnis gestreute zu einfallende Leistung im VIS) PE DE / 2 E0 6.4 1016 W 2 Unter der Annahme, dass die direkt gestreute Strahlung nur in einen Halbraum emittiert wird, ist das Intensitätsverhältnis IE/IS zwischen Erde und Sonne im VIS, wenn man sie von einem entfernten Sternsystem aus beobachtet, also: D I E 2 PE 2 E IS PS 4rE Geometrische und Technische Optik 2 3.3 10 10 Institut für Optik, Information und N. Lindlein Photonik 126+162 Detektion erdähnlicher Planeten Wahre Verhältnisse bei Beobachtung der Erde aus 10 Lichtjahren Entfernung: Durchmesser des Spiegels D=10 m, Wellenlänge =0.5 µm, rE=1 AE, IE/IS=3.3.10-10, d=10 Lichtjahre=9.46.1016 m Winkelabstand zwischen Erde und Sonne: rE 1.6 10 6 d Das Hauptmaximum der Airy-Disc der Erde liegt deshalb relativ zum Hauptmaximum der Airy-Disc der Sonne in der Bildebene des Teleskops bei der normierten Radial-Koordinate: ˆ D 31.6 Aus asymptotischem Verhalten der Airy-Verteilung der Sonne folgt für die Intensität des nächstgelegenen Nebenmaximums relativ zum Hauptmaximum: cos ˆ 0.75 1 2 I S ˆ 8 4 3 2.6 10 6 Das Bild der Erde wäre I S 0 ˆ relativ zum „Störlicht“ der I E 0 I E 0 / I S 0 3.3 10 10 4 10 I S ˆ I S ˆ / I S 0 2.6 10 6 Geometrische und Technische Optik Sonne also immer noch um den Faktor 10000 dunkler! Institut für Optik, Information und N. Lindlein Photonik 126+163 Detektion erdähnlicher Planeten Abschätzung der Strahlungsleistung PTele in Teleskop mit Spiegeldurchmesser D für Beobachtung der Erde aus einer großen Entfernung d: D/m D / 2 PE D 16 10 W 2 2 d 8 d d / Lichtjahr 2 PTele PE 2 2 Machen wir weiter die stark vereinfachende Annahme, dass all diese Strahlung in Form von Photonen der Wellenlänge =0.5 µm vorliegt, entspräche dies einer einfallenden Photonenrate N/t (Anzahl Photonen pro Zeit) von: 2 PTele PTele N D/m 200 / s t h Photon hc d / Lichtjahr Beispiel: D=10 m, d=10 Lichtjahre Pro Sekunde fallen gerade ca. 200 Photonen in den Spiegel, der den derzeit maximal herstellbaren Durchmesser hat. Selbst von Alpha Centauri aus mit d=4.34 Lichtjahre wären es nur ca. 1000 Photonen/s. In der Praxis beobachtet man nur in einem gewissen Spektralbereich noch deutlich weniger Photonen. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+164 Detektion erdähnlicher Planeten Verbesserte Beobachtung von Planeten im IR (Beispiel Erde): Planeten absorbieren den größten Teil der einfallenden Sonnenstrahlung und geben die Energie wieder als IR-Strahlung ab. Auf der Erde werden (1-)=63.3% der einfallenden Sonnenstrahlung mit Maximum bei 500 nm Wellenlänge (Effektiv-Temperatur Sonne TS=5778 K) absorbiert und dann als Infrarot-Strahlung abgestrahlt. Die effektive Temperatur TE der Erde lässt sich damit aus der Energie-Bilanz und dem Stefan-Boltzmann-Gesetz berechnen: 2 2 Pabsorbiert W DE DE 4 8 E0 1 PAbstrahlung 4 TE mit 5.67 10 m2K 4 2 2 TE 4 E0 1 248 K 4 Laut Wienschem Verschiebungsgesetz liegt das Strahlungsmaximum der Erde unter Annahme eines schwarzen Körpers deshalb bei der Wellenlänge: 2898 µm K E 11.7 µm TE Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+165 Detektion erdähnlicher Planeten M , T dAd PE , IR PS , IR 2hc 2 5 1 dAd hc exp 1 kT 4 DE / 2 M E , TE DE 2 4 DS / 2 M E , TS DS 2 exphc / E kTS 1 1.4 10 7 exphc / E kTE 1 2 http://upload.wikimedia.org/wikipedia/commons/0/0e/ BlackbodySpectrum_loglog_150dpi_de.png Aus dem Planckschen Strahlungsgesetz für schwarze Strahler lässt sich dann ermitteln, wie viel Strahlung PE,IR die Erde bzw. PS,IR die Sonne in einem schmalen Spektralbereich bei E=11.7 µm emittieren bzw. wie groß das Verhältnis dort ist: Im IR ist das Helligkeitsverhältnis Erde/Sonne also um fast einen Faktor 500 größer als im VIS und der Photonenfluss ist auch deutlich größer! Aber die Auflösung ist deutlich geringer (wegen größer), so dass der nötige Spiegeldurchmesser entsprechend größer wäre! Institut für Optik, Geometrische und Technische Optik Information und Photonik N. Lindlein 126+166 Detektion erdähnlicher Planeten Mögliche Verbesserungen zur direkten Beobachtung erdähnlicher Planeten: „Koronograph“: Durch eine Blende wird das direkt vom Stern kommende Licht absorbiert, während das schräg kommende Licht außerhalb der Achse auf den Detektor fällt. Bei Planeten um Sterne müsste die Blende aber sehr weit weg sein. „Nulling“-Interferometrie: Durch eine Maske soll das Sternenlicht auf der Achse negativ interferieren, während das außeraxiale Licht des Planeten nicht beeinflusst wird. Komplizierte wellenoptische Berechnung. Mehrere Spiegel werden in einer Reihe interferometrisch zu einem Teleskop der Länge L gekoppelt, das zumindest in einer Richtung die Auflösung eines Spiegels mit scheinbarem Durchmesser L hat. Auswertung muss auch wellenoptisch erfolgen. Natürlich sollten all diese Teleskope im Weltall platziert werden oder eine aufwändige adaptive Optik besitzen, um die Auflösungsreduktion durch Turbulenzen der Atmosphäre zu vermeiden. Geometrische und Technische Optik Institut für Optik, Information und N. Lindlein Photonik 126+167