1.Übung - EMV

1.Übung
Schaltungstechnik
SS2009
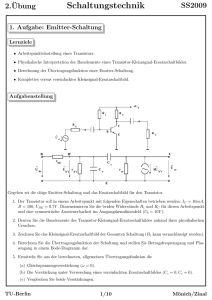
1. Aufgabe: Leistungsanpassung
Lernziele
• Komplexen Darstellung elektrischer Größen.
• Leistungsanpassung für komplexe Impedanzen.
• Leistungs-, Spannugs-, Stromquelle.
Aufgabenstellung
RT
1. Ausgehend von dem Ausdruck für die mittlere Leistung im Zeitbereich (P = T1 0 p(t) dt ;
p(t) = u(t) · i(t)), soll der Leistungsausdruck für die Signale u(t) = Û cos(ωt + ϕu ) und
i(t) = Iˆ cos(ωt + ϕi ) in komplexer Form hergeleitet werden. Dabei gilt folgende Notationskonvention:
Komplexe Größen:
Z = ZRe + j ZIm = |Z| ej ϕz
Komplexe Signale:
U = Ũ ejωt = Û ej ϕu ejωt
u(t) = <{U } = 12 (U + U ∗ )
2. Die folgende Schaltung zeigt eine reale Spannungsquelle (Urquelle mit komplexer Spannungsamplitude
Ũ0 (komplexer Zeiger, Phasor) + komplexe Innenimpedanz Z i ) die eine Last der komplexen Impedanz
Z L versorgt.
Zi
~
~
IL
~
U0
UL
ZL
(a) Berechnen Sie die an die Last abgegebene Wirkleistung.
(b) Berechnen Sie die Lastimpedanz für eine maximale, abgegebene Wirkleistung. Hinweis: Die Bedingung muss jeweils für den Realteil und den Imaginärteil der Lastimpedanz getrennt formuliert
werden.
(c) Es sei nun: Z L = RL , Z i = Ri und Ũ0 = U0 . Welche Anforderungen stellt man an eine ideale Spannungsquelle und an eine ideale Stromquelle bezüglich kleiner Änderungen des Lastwiderstandes?
Formulieren Sie die Bedingungen für Ri um diesen Anforderungen gerecht zu werden.
TU-Berlin
1/11
Mönich/Zinal
Schaltungstechnik
1.Übung
SS2009
Lösung
1. Herleitung des Leistungsausdruckes für komplexe Signale:
1
P =
T
Z
T
Û Iˆ cos(ωt + ϕu ) cos(ωt + ϕi ) dt
(1)
0
1
=
Û Iˆ
2T
Z
1
=
Û Iˆ
2T
Z
T
[cos(2ωt + ϕu + ϕi ) + cos(ϕu − ϕi )] dt
(2)
Z T
1
cos(2ωt + ϕu + ϕi ) dt + Û Iˆ
cos(ϕu − ϕi ) dt
2T
0
{z
}
|
{z
}
(3)
0
T
0
|
=0
T cos(ϕu −ϕi )
1 ˆ
1
Û I cos(ϕu − ϕi ) = Û Iˆ <{ej ϕu e−j ϕi }
2
2
=
1
<{Ũ I˜∗ }
2
=
(4)
2. (a) Berechnung der an die Last abgegebenen Wirkleistung:
ŨL = Ũ0
ZL
Zi + ZL
(Spannungsteiler)
(5)
ŨL
1
I˜L =
= Ũ0
ZL
Zi + ZL
ŨL I˜L∗ =
PL =
(6)
|Ũ0 |2
Z L Ũ0 Ũ0∗
=
Z
L
|Z i + Z L |2
(Z i + Z L ) (Z i + Z L )∗
(7)
1
|Ũ0 |2
1
ZL,Re
1
<{ŨL I˜L∗ } = <{Z L }
= |Ũ0 |2
2
2
2
|Z i + Z L |
2
(ZL,Re + Zi,Re )2 + (ZL,Im + Zi,Im )2
(8)
(b) Berechnung der Lastimpedanz für maximale Leistungsaufnahme: (Z i und Ũ0 seien gegeben.)
i. Bedingung für den Imaginärteil:
∂PL
1
0 − 2 (ZL,Im + Zi,Im ) ZL,Re
= |Ũ0 |2
∂ZL,Im
2
[(ZL,Re + Zi,Re )2 + (ZL,Im + Zi,Im )2 ]2
!
=0
(9)
=⇒
ZL,Im = −Zi,Im
(1.Bedingung)
ii. Bedingung für den Realteil:
∂PL
1
(ZL,Re + Zi,Re )2 + (ZL,Im + Zi,Im )2 − 2 (ZL,Re + Zi,Re ) ZL,Re !
= |Ũ0 |2
=0
∂ZL,Re
2
[(ZL,Re + Zi,Re )2 + (ZL,Im + Zi,Im )2 ]2
!
2
2
2
ZL,Re
+ Zi,Re
+ 2 ZL,Re Zi,Re + (ZL,Im + Zi,Im )2 − 2 ZL,Re
− 2 ZL,Re Zi,Re = 0
q
2
=⇒ ZL,Re = Zi,Re
+ (ZL,Im + Zi,Im )2
(2.Bedingung)
=⇒
iii. Diskussion der 2.Bedingung:
A. Bedingung 1 ist erfüllt:
ZL,Re = Zi,Re
B. Reelle Last (ZL,Re = RL , ZL,Im = 0):
q
2
2
RL = Zi,Re
+ Zi,Im
= |Z i |
TU-Berlin
2/11
(10)
(11)
(12)
(13)
(14)
(15)
Mönich/Zinal
1.Übung
2. (c)
Schaltungstechnik
i. Spannungsquelle:
∆UL
−→ 0 =⇒
∆RL
ii. Stromquelle:
∆IL
−→ 0 =⇒
∆RL
∂UL
RL + Ri − RL
= U0
−→ 0
∂RL
(RL + Ri )2
∂IL
0−1
= U0
−→ 0
∂RL
(RL + Ri )2
SS2009
=⇒
=⇒
Ri −→ 0
(16)
Ri −→ ∞
(17)
Simulationsschaltung
Schaltung ausschließlich mit Ohmschen Wideständen:
1. Variieren Sie den Lastwiderstand RL im Bereich 100Ω − 4kΩ (Benutzen Sie dafür den DC-Sweep! ).
2. Stellen Sie die im Lastwiderstand verbrauchte Leistung als Funktion des Widerstandswertes dar.
3. Überprüfen Sie die Übereinstimmung des Widerstandswertes für eine maximale Leistung mit der Theoretischen Vorhersage (Beachten Sie, dass die positive Stromrichtung durch ein Bauelement von pin 1
nach pin 2 festgelegt ist! ).
Schaltung mit Ohmschen Wideständen und Blindelementen:
1. Führen Sie für die obige Schaltung eine Simulation (AC-Sweep) im Frequenzbereich 10Hz − 500kHz
durch.
2. Stellen Sie die an die Lastimpedanz abgegebene Wirkleistung als Funktion der Frequenz dar (Beachten
Sie, dass PSpice keine komplexen Größen ausgibt, sondern nur Betrag, Phase, Real- und Imaginärteil.
Der Ausdruck in Gl. (4) für die Wirkleistung muss daher PSpice-tauglich umgeformt werden.).
3. Bei welcher Frequenz erreicht die zugeführte Wirkleistung ihr Maximum? Überprüfen Sie die Richtigkeit
des abgelesenen Wertes anhand der Rechnung aus Abschnitt 2b.
TU-Berlin
3/11
Mönich/Zinal
Schaltungstechnik
1.Übung
SS2009
2. Aufgabe: Beidseitige Leistungsanpassung
Lernziele
• Vierpol-Parameter.
• Übertragungsfunktion eines Vierpols (belastet versus unbelastet).
• Beidseitige Leistungsanpassung von Vierpolen.
Aufgabenstellung
Qelle
Ri
~
U0
Last
Vierpol (Tiefpass)
R
~
~
U1
C
UL
~
IL
RL
Die obige Schaltung zeigt einen Vierpol (Tiefpass) der mit einer realen Spannungsquelle und einer Last
beschaltet ist.
1. Berechnen Sie die Parameter des Vierpols für die Impedanz-Vierpolgleichungen. Hinweis: Siehe Anhang
Vierpolgleichungen auf der Homepage.
2. Berechnen Sie die Übertragungsfunktion des Tiefpasses im Idealfall (unbelastet).
3. Berechnen Sie die Übertragungsfunktion der gesamten schaltung ( ŨŨL ) und zeigen Sie daß die Übertra0
gungsfunktion für Ri −→ 0 und RL −→ ∞ in die des idealen Tiefpasses übergeht.
4. Es seien nun R und C des Tiefpasses fest vorgegeben. Wie müssen RL und Ri gewählt werden um
die von der Urquelle an die Last abgegebene Wirkleistung zu maximieren (beidseitige Anpassung)?
Hinweis: Man löst zwei Teilprobleme, das eine mit bekanntem RL , das andere mit bekanntem Ri und
bekommt somit zwei Gleichungen mit zwei Unbekannten.
TU-Berlin
4/11
Mönich/Zinal
Schaltungstechnik
1.Übung
SS2009
Lösung
1. Berechnung der Z-Vierpolparameter:
~
~
I1
I2
R
~
~
U1
U2
C
(a) Z-Vierpolgleichungen:
Ũ1 = Z 11 I˜1 + Z 12 I˜2
Ũ2 = Z 21 I˜1 + Z 22 I˜2
(b) Berechnung der Parameter:
Ũ1 1
Z 11 =
=R+
jωC
I˜1 I˜ =0
2
Ũ2 1
=
Z 21 =
˜
jωC
I1 ˜
Z 12
Z 22
I2 =0
Ũ1 =
I˜2 (18)
1
jωC
(19)
Ũ2 1
=
=
˜
I2 I˜ =0 j ω C
(20)
=
I˜1 =0
1
2. Tiefpass-Übertragungsfunktion im Idealfall (I˜2 = 0):
1
1
Ũ2
jωC
=
=
1
1+jωRC
R + jωC
Ũ1
(Spannungsteiler!)
(21)
3. Übertragungsfunktion der gesamten Schaltung:
Z RL ||C =
F (j ω) =
=
lim F (j ω) =
Ri →0
RL →∞
TU-Berlin
RL
jωC
RL +
1
jωC
=
RL
1 + j ω C RL
Z RL ||C
ŨL
=
Ri + R + Z RL ||C
Ũ0
RL
1+j ω C RL
Ri + R + 1+j Rω LC RL
=
(22)
(Spannungsteiler!)
RL
(Ri + R + RL ) + j ω C RL (Ri + R)
RL
1
=
RL →∞ (R + RL ) + j ω C RL R
1+jωRC
lim
5/11
(23)
(24)
(25)
Mönich/Zinal
Schaltungstechnik
1.Übung
SS2009
4. (a) 1.Teilproblem (RL sei bekannt):
R
Ze
Ze
RL
= R+
=
1 + j ω C RL
s
!
Ri = |Z e | =
RL
C
RL
R+
1 + ω 2 C 2 RL2
RL
R+
1 + ω 2 C 2 RL2
2
+
−j
ω C RL2
1 + ω 2 C 2 RL2
ω C RL2
1 + ω 2 C 2 RL2
(26)
2
(27)
(b) 2.Teilproblem (Ri sei bekannt):
Ri
R
C
Za
RL
Za
Ri + R
Ri + R
ω C (Ri + R)2
=
=
−j
1 + j ω C (Ri + R)
1 + ω 2 C 2 (Ri + R)2
1 + ω 2 C 2 (Ri + R)2
s
2 2
Ri + R
ω C (Ri + R)2
!
= |Z a | =
+
1 + ω 2 C 2 (Ri + R)2
1 + ω 2 C 2 (Ri + R)2
(28)
(29)
(c) (27) und (29) bilden zwei Gleichungen mit zwei Unbekannten.
Simulationsschaltung
1. Führen Sie für die obige Schaltung eine Simulation (AC-Sweep) im Frequenzbereich 10Hz − 10M Hz
durch.
2. Stellen Sie das Bode-Diagramm (Phasen- u. Amplitudengang) des Tiefpasses dar.
3. Ermitteln Sie, sowohl rechnerisch als auch aus den Simulationsergebnissen, die Grenzfrequenz des Tiefpasses.
TU-Berlin
6/11
Mönich/Zinal
Schaltungstechnik
1.Übung
SS2009
3. Aufgabe: Hochfrequenz-Dämpfungsglied
Lernziele
• Großsignal- versus Kleinsignalanalyse (im Spezialfall: Gleichstrom- versus Wechselstromanalyse).
• Entkopplung von Gleichstrom- und Wechselstromkreis einer Schaltung.
• Arbeitspunkteinstellung von nicht-linearen Bauelementen (graphische und algebraische Methode).
• Kleinsignal-Ersatzschaltbilder einer normalen (PN-) bzw. einer PIN-Diode.
Aufgabenstellung
RDC
L
RAC
ID
C
U DC
C
UD
RL
~
U AC
UDC = 1V, RDC =?, UAC =?, RAC = 50Ω, RL >> rd ,
C, L >> 1
Die obige Schaltung stellt eine vereinfachte Variante eines Hochfrequenz-Dämpfungsgliedes dar. Die verwendete PIN-Diode dient dabei als gleichstromgesteuerter Wechselstromwiderstand. Hinweis: Die beiden
Kondensatoren und die Spule dienen ausschließlich dem Zweck der Trennung von Gleichstrom- und Wechselstromschaltung.
1. Was versteht man unter den Begriffen: Großsignal- und Kleinsignalanalyse?
2. Großsignal-Analyse1 :
(a) Zeichnen Sie den für die Gleichstrombetrachtung relevanten Teil der Schaltung.
UD
(b) Es sei die Kennlinie der Diode mit ID = Is (e n UT − 1) gegeben. Dabei ist der Emissionskoeffizient
n = 2, die Temperaturspannung UT = 26mV und der Sättigungssperrstrom Is = 10nA.
Welcher Unterschied besteht zwischen dem Gleichstrom- und dem Wechselstrom-Widerstand eines
nichtlinearen Bauelementes? Wie lässt sich der jeweilige Widerstand für die Diode berechnen?
(c) Es soll ein differezieller Widerstand von 50Ω eingestellt werden. Welcher Wert muß für RDC gewählt
werden? Ermitteln Sie den Wert
i. algebraisch mit Hilfe der Gleichungen und
ii. graphisch anhand der angegebenen Kennlinien.
TU-Berlin
7/11
Mönich/Zinal
Schaltungstechnik
1.Übung
SS2009
3. Kleinsignal-Analyse:
(a) Zeichnen Sie das Kleinsignal-Ersatzschaltbild einer Diode, eines pn-Übergangs und eines p-i-nÜbergangs (für hohe Frequenzen ).
(b) Zeichnen Sie das Kleinsignal-Ersatzschaltbild der gesamten Schaltung.
Lösung
1. In Schaltungen mit nichtlinearen Bauelemeten sind im Allgemeinen zwei Arten von Signalen zu beobachten:
(a) Ein relativ kräftiges Signal (Großsignal) welches große Bereiche der nichtlinearen Kennlinien
durchfährt. Dieses Großsignal kann ein sinusförmiges Signal sein wie z.B. bei Mischern, Modulatoren usw. Es kann aber auch ein Gleichsignal sein welches einen bestimmten Punkt auf der
nichtlinearen Kennlinie (Arbeitspunkt) einstellt wie z.B bei Verstärkern.
(b) Ein relativ schwaches Nutzsignal (Kleinsignal) welches nur einen möglichst kleinen Bereich der
nichtlinearen Kennlinie durchfährt. Der Ort dieses Bereichs auf der Kennlinie wird durch das
Großsignal bestimmt. Bezüglich des Kleinsignals kann die Kennlinie am jeweiligen Ort linearisiert
werden. Das Bauelement kann damit durch ein lineares Netzwerk modelliert werden. Dieses lineare
Netzwerk ist im Falle eines Gleich-Großsignals zeitinvariant (Kleinsignal-Verstärker). Im Falle eines
Wechsel-Großsignals ist es jedoch zeitvariant (Mischer).
(Kleinsignal-Ersatzschaltbild)
Großsignal-Analyse −→ Lineares Netzwerk −→ Kleinsignal-Analyse
2. (a) Gleichstrom-Ersatzschaltbild:
(b) Der Gleichstromwiderstand ist das Verhältnis von Gleichspannung (UA ) und Gleichstrom (IA )im
Arbeitspunkt. Der Wechselstromwiderstand ist das Verhältnis von Änderung der Gleichspannung
(∆UA ) und Änderung des Gleichstroms (∆IA ). Er kann durch die Linearisierung der Kennlinie im
jeweiligen Arbeitspunkt ermittelt werden.
U UD,A
RG,A =
=
(30)
UD,A
I UA ,IA
Is (e n UT − 1)
dU 1
1
n UT − UnD,A
rd,A =
=
=
=
e UT
(31)
UD,A
dI dI UA ,IA
I
s
I
s
n UT
dU UA ,IA
e
n UT
TU-Berlin
8/11
Mönich/Zinal
Schaltungstechnik
1.Übung
2. (c)
SS2009
i. Algebraisch:
Umformung von (31) =⇒ UD,A = −n UT ln
rd,A Is
n UT
(32)
= −2 × 26mV × ln
50Ω × 10nA
2 × 26mV
UD,A
= 0.6007mV
0.6007V
Einsetzen in ID (UD ) =⇒ ID,A = Is (e n UT − 1) = 10nA × (e 2×26mV − 1)=1.04mA
RDC =
UDC − UD,A
1V − 0.6007V
=
= 383.9348Ω
ID,A
1mA
(33)
(34)
(35)
ii. Graphisch:
Ausschnitt aus der Dioden-Kennlinie
differenzieller Widerstand
100
0.009
90
0.008
80
0.007
70
0.006
60
Id [A]
rd [Ω]
0.01
0.005
50
0.004
40
0.003
30
0.002
20
0.001
10
0
0
0.2
0.4
0.6
0.8
1
Ud [V]
0
0
0.2
0.4
0.6
0.8
1
Ud [V]
3. (a) Dioden-Kleinsignal-Ersatzschaltbilder:
TU-Berlin
9/11
Mönich/Zinal
1.Übung
Schaltungstechnik
SS2009
3. (b) Kleinsignal-Ersatzschaltbild der Schaltung:
Simulationsschaltung
1. Führen Sie für die obige Schaltung eine Simulation (Transient! ) im Zeitbereich 0 − 50µs durch. Dabei
soll der Widerstand RDC als Parameter im Bereich 100Ω − 1kΩ in 100Ω-Schritten variiert werden
(Parametric! ).
2. Stellen Sie die parametrische Kurvenschar der am Lastwiderstand anliegenden Spannung als Funktion
der Zeit dar und interpretieren Sie die Ergebnisse. Wodurch entsteht die Phasenverschiebung zwischen
den einzelnen Kurven?
TU-Berlin
10/11
Mönich/Zinal
1.Übung
Schaltungstechnik
SS2009
Hausufgaben
Rechenaufgabe: Koaxiale Messleitung mit Tastkopf
Messobjekt
Tastkopf
Oszilloskop−Eingang
Koaxialleitung
R TK
~
U0
R OZ C OZ
~
Um
C TK
ROZ = 1M Ω, COZ = 25pF
Oszilloskope besitzen hochohmige, kapazitive Eingänge. Dies führt zu einem Tiefpassverhalten welches die
Messbandbreite des Gerätes beschränkt. Benutzt man als Messleitung eine Koaxialleitung, um Störeinwirkungen durch kapazitive und induktive Verkoppelung zu verhindern, wird die Messbandbreite durch den
Kapazitätsbelag den die Koaxialleitung aufweist weiter beschränkt.
Um dies zu kompensieren ist den meisten Koaxialmessleitungen ein Tastkopf vorgeschaltet. Mit dem Tastkopf
lässt sich auch eine Spannungsteilung und somit eine Messbarkeit von höheren Spannungen erreichen.
1. Berechnen Sie die Z- und die Y-Vierpolparameter für den Tastkopf-Vierpol.
2. Berechnen Sie die Übertragungsfunktion der Gesamtanordnung
Ũm
.
Ũ0
0
3. Die Koaxialleitung habe einen Kapazitätsbelag CK
= 50pF/m und eine Länge L = 1.5m. Welche
Werte müssen RT K und CT K haben um ein 10:1 Spannungsverhältnis und eine Frequenzkompensation
zu erreichen?
Simulationsaufgabe:
1. Protokollieren Sie die Simulationsergebnisse der Übungsaufgaben 1, 2 und 3.
Zusatzinformationen für Interessierte
PIN-Dioden:
Eine p-i-n Diode besitzt im Vergleich zu einer normalen pn-Diode eine zusätzliche undotierte Halbleiterschicht
zwischen den beiden mit Donatoren (n) und Akzeptoren (p) dotierten Schichten. Der Buchstabe i (intrinsic)
kommt vom Englischen und sagt aus, daß die Ladungsträger (Elektronen u. Löcher) in dieser Schicht ausschließlich aus den Valenzbindungen des reinen Halbleiterkristalls stammen.
Die Ladungsträger in der i-Schicht haben eine relativ hohe Lebensdauer (τ ) verglichen mit der Lebensdauer
von Ladungsträgern in doetierten Halbleiterschichten. Da eine Diode erst dann in den Sperrbetrieb gelangt
wenn alle Ladungsträger rekombiniert sind, kann sie einen negativen Puls der Dauer tp << τ leiten. Gibt man
nun ein Hochfrequentes Signal der Frequenz f >> τ1 auf die Diode dann verhält sie sich wie ein ohmscher
Widerstand dessen Wert sich durch die Überlagerung eines konstanten Stromes sehr variabel einstellen lässt.
Die relativ dicke i-Schicht hat desweiteren eine geringe Sperrschichtkapazität zur Folge. Deshalb sind pinDioden auch als Hochfrequenzschalter mit hoher Sperrdämpfung einsetzbar.
TU-Berlin
11/11
Mönich/Zinal