Schaltungstechnik - EMV

Schaltungstechnik
2.Übung
SS2009
1. Aufgabe: Emitter-Schaltung
Lernziele
• Arbeitspunkteinstellung eines Transistors.
• Physikalische Interpretation der Bauelemente eines Transistor-Kleinsignal-Ersatzschaltbildes.
• Berechnung der Übertragungsfunktion einer Emitter-Schaltung.
• Komplettes versus vereinfachtes Kleinsignal-Ersatzschaltbild.
Aufgabenstellung
+U
R
R
~
U
R
E
L
g
B’
r
be
C
C
g
B
B
~
U
R
1
b
C
C
bb’
~
U
b’e
r
b’e
C
c
r
e
ce
~
SU
~
U
b’e
ce
E
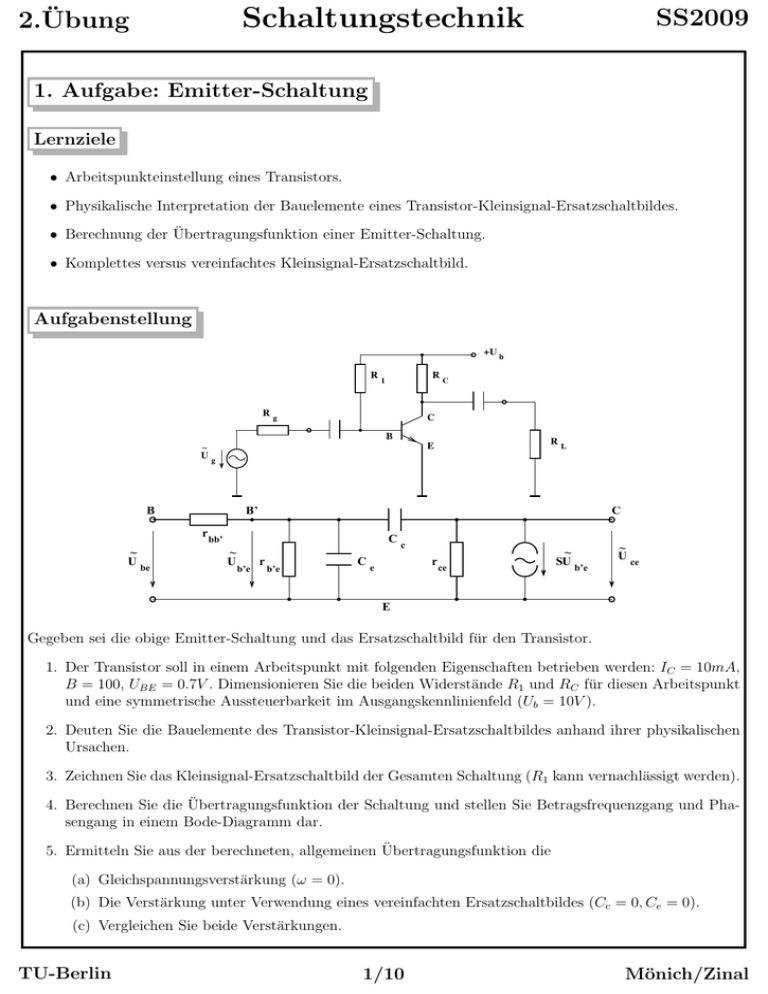
Gegeben sei die obige Emitter-Schaltung und das Ersatzschaltbild für den Transistor.
1. Der Transistor soll in einem Arbeitspunkt mit folgenden Eigenschaften betrieben werden: IC = 10mA,
B = 100, UBE = 0.7V . Dimensionieren Sie die beiden Widerstände R1 und RC für diesen Arbeitspunkt
und eine symmetrische Aussteuerbarkeit im Ausgangskennlinienfeld (Ub = 10V ).
2. Deuten Sie die Bauelemente des Transistor-Kleinsignal-Ersatzschaltbildes anhand ihrer physikalischen
Ursachen.
3. Zeichnen Sie das Kleinsignal-Ersatzschaltbild der Gesamten Schaltung (R1 kann vernachlässigt werden).
4. Berechnen Sie die Übertragungsfunktion der Schaltung und stellen Sie Betragsfrequenzgang und Phasengang in einem Bode-Diagramm dar.
5. Ermitteln Sie aus der berechneten, allgemeinen Übertragungsfunktion die
(a) Gleichspannungsverstärkung (ω = 0).
(b) Die Verstärkung unter Verwendung eines vereinfachten Ersatzschaltbildes (Cc = 0, Ce = 0).
(c) Vergleichen Sie beide Verstärkungen.
TU-Berlin
1/10
Mönich/Zinal
Schaltungstechnik
2.Übung
SS2009
Lösung
1. Dimensionierung der Widerstände RC und R1 :
20mA
15mA
10mA
5mA
0A
RC =
IB,A =
R1 =
0V
1V
IC(Q1)
2V
3V
4V
5V
6V
7V
8V
9V
10V
V_UCE
10V − 5V
Ub − UCE,A
=
= 500Ω
IC,A
10mA
(1)
10mA
IC,A
=
= 0.1mA
BA
100
(2)
Ub − UBE,A
10V − 0.7V
=
= 93kΩ
IB,A
0.1mA
(3)
2. Physikalische Interpretation der Bauelemente des Transistor-Kleinsignal-Ersatzschaltbildes:
(a) rbb0
(b) rb0 e
(c) Ce
(d) Cc
(e) rce
(f) S Ũb0 e
TU-Berlin
2/10
Mönich/Zinal
Schaltungstechnik
2.Übung
SS2009
3. Kleinsignal-Ersatzschaltbild:
4. (a) Berechnung der Übertragungsfunktion:
~
Ig
~
Ug
Schl. I
~
I be
Cc
Kn. I
R2
B’
~
U
r
b’e
b’e
Ce
Kn. II
C
R
Schl. II
3
~
SU
~
U
b’e
L
E
Schl. I:
Schl. II:
Kn. I:
Kn. II:
(5) in (6):
(8) in (4):
=⇒
Ũg − Ũb0 e − R2 I˜g = 0
Ũb0 e − ŨL −
=⇒
1 ˜
Ibe = 0
j ω Cc
Ũb0 e = Ũg − R2 I˜g
=⇒
1
I˜g − (
+ j ω Ce ) Ũb0 e − I˜be = 0
rb0 e
ŨL
I˜be −
− S Ũb0 e = 0
R3
=⇒
I˜be = j ω Cc (Ũb0 e − ŨL )
=⇒
Ũb0 e =
(5)
1
I˜g = (
+ j ω Ce ) Ũb0 e + I˜be
rb0 e
ŨL
I˜be =
+ S Ũb0 e
R3
1
I˜g = (
+ j ω (Ce + Cc )) Ũb0 e − j ω Cc ŨL
rb0 e
Ũb0 e = Ũg − (
(4)
R2
+ j ω (Ce + Cc ) R2 ) Ũb0 e + j ω Cc R2 ŨL
rb0 e
(6)
(7)
(8)
(9)
Ũg + j ω Cc R2 ŨL
1 + rR02 + j ω (Ce + Cc ) R2
(10)
ŨL
+ S Ũb0 e
R3
(11)
b e
(5) = (7):
(10) in (12):
j ω Cc (Ũb0 e − ŨL ) =
(
1
+ j ω Cc ) ŨL = (−S + j ω Cc ) Ũb0 e
R3
(12)
(
1
Ũg + j ω Cc R2 ŨL
+ j ω Cc ) ŨL = (−S + j ω Cc )
R3
1 + rR02 + j ω (Ce + Cc ) R2
(13)
b e
TU-Berlin
3/10
Mönich/Zinal
Schaltungstechnik
2.Übung
=⇒
Vu =
=
−ω
|{z}
−S+j ω Cc
ω (Ce +Cc ) R2
R2
+j
b0 e
ŨL
=
Ũg
2
SS2009
1+ r
1
R3
+ j ω Cc −
(14)
j ω Cc R2 (−S+j ω Cc )
R
1+ r 2 +j ω (Ce +Cc ) R2
b0 e
R2 R3 (2 Cc2
R3 (−S + j ω Cc )
+ Cc Ce ) + j ω [R2 (Cc + Ce ) + Cc R3 (1 +
R2
rb0 e
− S R2 )] + 1 +
R2
rb0 e
(15)
(j ω)2
3. (b) Darstellung von Betrags- und Phasenfrequenzgang:
Zahlenbeispiel: Ein Transistor habe für den Arbeitspunkt (UCE = 5V, IC,A = 1mA) folgende
Kenndaten: rbb0 = 88Ω, rb0 e = 2kΩ, rce = 40kΩ, Ce = 5nF, Cc = 22pF .
Desweiteren wählen wir:Ub = 10V, Rg = 0, RL = 10kΩ.
Betragsfrequenzgang
45
40
|V| [dB]
35
30
25
20
15
10
5
0
5
10
6
7
10
8
10
ω [rad/s]
10
9
10
10
10
Phasengang
180
160
140
φV [°]
120
100
80
60
40
20
0
5
10
6
7
10
8
10
ω [rad/s]
10
9
10
10
10
4. (a) Gleichspannungsverstärkung (ω = 0):
V u |ω=0 =
rb0 e
−S R3
=
−
S R3
rb0 e + R2
1 + rR02
rb0 e >>R2
≈
−S R3
(16)
b e
(b) Vereinfachtes Ersatzschaltbild (Ce = 0, Cc = 0):
V u |Ce =0,Cc =0 =
−S R3
rb0 e
=−
S R3
R2
rb0 e + R2
1+ r0
rb0 e >>R2
≈
−S R3
(17)
b e
(c) Vergleich von (a) und (b): Der Gültigkeitsbereich des vereinfachten Ersatzschaltbildes ist jener
Bereich in dem die Spannungsverstärkung einen (näherungsweise) konstanten Verlauf aufweist. Ihr
Wert entspricht der Gleichspannungsverstärkung.
TU-Berlin
4/10
Mönich/Zinal
2.Übung
Schaltungstechnik
SS2009
Simulationsschaltung
1. Bestimmen Sie den Wert von R1 für den Transistor-Arbeitspunkt: UCE = 5V , IC = 10mA.
Hinweis: Dazu muss nur Bias Point Detail unter Analysis Setup aktiviert sein! Die Gleichspannungen
und -ströme können durch Aktivierung der beiden Schaltflächen V und I, im Schematics-Fenster,
sichtbar gemacht werden.
2. Stellen Sie das Bode-Diagramm des Verstärkers, im Bereich 1Hz − 10GHz, dar. Bestimmen Sie daraus
die Grenzfrequenz sowie die Transitfrequenz des Verstärkers.
2. Aufgabe: Rückkopplungskreis
Lernziele
• Umgang mit Blockschaltbildern.
• Berechnung der Übertragungsfunktion eines einfachen Rückkopplungskreises.
Aufgabenstellung
Vr
~
Ur
~
Ue
−
+
+
~
Ud
V
~
Ua
Das obige Bild zeigt ein Blockschaltbild eines einfachen Rückkopplungskreises mit Funktionsblöcken. Dabei ist
jeder Funktionsblock durch seine Übertragungsfunktion gekennzeichnet, welche das Verhältnis von Ausgangszu Eingangssignal angibt. Diese Form der Darstellung dient der Übersichtlichkeit beim Entwurf sowie bei der
Analyse von Schaltungen.
1. Berechnen Sie die Übertragungsfunktion der gesamten Schaltung.
TU-Berlin
5/10
Mönich/Zinal
Schaltungstechnik
2.Übung
SS2009
Lösung
Sumationselement:
Vorwärts-Übertragungsblock:
Rückkopplungs-Übertragungsblock:
(20)−→(18)−→ (19):
Übertragungsfunktion:
Ũd = Ũe ± Ũr
(18)
Ũa = V Ũd
(19)
Ũr = V r Ũa
(20)
Ũa = V (Ũe ± V r Ũa )
(21)
Ũa
V
=
1∓V Vr
Ũe
(22)
Hausufgaben
Rechenaufgabe: Arbeitspunkt-Einstellung, Kleinsignal-Ersatzschaltbilder.
+U
R
R
~
U
b
1
C
g
B
E
g
RC
RL
+U
R
R
~
U
g
g
E
R
1
b
C
C
R
B
+U
L
b
1. Dimensionieren Sie die beiden obigen Schaltungen für den in Aufgabe 1 festgelegten Arbeitspunkt.
Hinweis: Bei der Basisschaltung kann R1 = 50Ω gewählt werden.
2. Zeichnen Sie die Kleinsignal-Ersatzschaltbilder unter Anwendung des in Aufgabe 1 gegebenen
Transistor-Ersatzschaltbildes.
Simulationsaufgabe:
1. Protokollieren Sie die Simulationsergebnisse der Übungsaufgabe 1.
TU-Berlin
6/10
Mönich/Zinal
Schaltungstechnik
2.Übung
SS2009
Zusatzinformationen für Interessierte
Regelungstechnische Exkursion:
Die in Gl. (15) dargestellte Übertragungsfunktion lässt sich durch wenige Substititutionen und Umformungen
auf eine Form bringen welche mittels regelungstechnischen Methoden leicht zu analysieren ist.
R (−S + j ω Cc ) ×
{z
}
|3
F (j ω) =
=FP D (j ω)
(j
|
ω)2
(23)
PD-Element
R2 R3 (2 Cc2
1
+ Cc Ce ) + j ω [R2 (Cc + Ce ) + Cc R3 (1 +
{z
=FP T 2 (j ω)
R2
rb0 e
− S R2 )] + 1 +
R2
rb0 e
(24)
}
PT2-Element
Zunächst führen wir eine komplexe Frequenz ω ein:
ω = α+jβ
p = j ω = −β + j α
,
(25)
Für die harmonische Zeitabhängigkeit ergibt sich damit:
ej ω t =
−β t
e|{z}
ej α t
|{z}
·
(26)
Ab- bzw. Aufkling-Term Harmonischer Term
• Proportional-Element mit Verzögerung II.Ordnung:
1
FP T 2 (p) =
p2
R2
R2
− S R2 )] + 1 +
+ Cc Ce ) +p [R2 (Cc + Ce ) + Cc R3 (1 +
{z
}
rb0 e
r0
|
{z
} | {z b e}
AN
(27)
R2 R3 (2 Cc2
|
BN
CN
q
CN
, 2D = √ABNNCN , Kp2 = C1N , wobei ω0 die Schwingfrequenz
Mit den Substitutionen ω0 =
AN
der ungedämpften Schaltung, D den Dämpfungsfaktor und Kp2 den Proportionalitätsfaktor darstellen,
gelangt man zu einer in der Fachliteratur üblichen Form:
FP T 2 (p) = 2
p
ω0
Kp2
+ 2D
p
ω0
(28)
+1
Aussagen über die Sabilität können anhand des Dämpfungsfaktors D gemacht werden:
D > 0 stabil
,
D = 0 grenzstabil (Schwingfall)
,
D < 0 instabil
(29)
• Proportional-Differential-Element:
FP D (p) = R3 S (−1 + p
Cc
)
S
(30)
Mit den Substitutionen Kp1 = R3 S und Tv =
Cc
S
gelangt man zu der Form:
FP D (p) = Kp1 (−1 + p Tv )
TU-Berlin
(31)
7/10
Mönich/Zinal
2.Übung
Schaltungstechnik
SS2009
Für diese standardisierten Übertragungselemente findet man in der regelungstechnischen Fachliteratur (z.B.
Taschenbuch der Regelungstechnik von Lutz und Wendt, Verlag Harri Deutsch) die ensprechenden BodeDiagramme und weitere Informationen.
Hinweis: Auf der Homepage kann ein Matlab-Programm zur Berechnung der Übertragungsfunktion und ihre
Pol-, Nullstellen, Schwingfrequenz und Dämpfungsfaktor heruntergeladen werden.
Kapazitäten des pn-Übergangs:
In einem pn-Übergang sind zwei physikalische Prozesse auszumachen, welche ein kapazitives Verhalten des
Übergangs zur Folge haben und dementsprechend durch Kapazitäten im dynamischen Ersatzschaltbild modelliert werden können.
• Sperrschichtkapazität: Die Weite der Raumladungszone (Wird auch Verarmungszone, engl.= depletion region, genannt, da sie an freien Ladungsträgern stark verarmt ist.), die in einem pn-Übergang
herrcht, variiert mit der an der Diode anligenden Spannung. Diese Variation der Zonenweite ist mit
dem abfließen oder zuführen von Ladungsträgern verbunden und kann daher durch eine Kapazität
beschrieben werden.
• Diffusionskapazität: Im Durchlassbereich ändert sich die Ladugsträgerkonzentration mit der anliegenden Spannung. Dies führt zur Speicherung einer sogenannten Diffusionsladung und kann damit auch
durch eine Kapazität modelliert werden.
Diese beiden Kapazitäten sind parallel geschaltet. Ist die Diode in Sperrichtung gespeist so ist die Diffusionskapazität klein im Vergleich zur Sperrschichtkapazität und kann vernachlässigt werden. Bei hohen Strömen
im Durchlassbereich dagegen, ist die Diffusionskapazität größer als die Sperrschichtkapazität so daß letztere
vernachlässigt werden kann.
Transistor-Ersatzschaltbilder:
Bemerkung: Eine ausführliche Abhandlung über T-ESB ist in folgendem Fachbuch zu finden: J. Dosse, Der
Transistor, 4.Auflage, 1962, R.Oldenburg München.
Man unterscheidet stationäre (Großsignal- ) und dynamische (Kleinsignal- ) Ersatzschaltbilder.
Die Kleinsignal-Ersatzschaltbilder für Transistoren lassen sich im wesentlichen in zwei Hauptgruppen unterteilen die sich in der Herangehensweise bei der Modellierung unterscheiden:
1. Formale, Vierpol-Ersatzschaltbilder: Dabei wird der Transistor durch vier, im Allgemeinen komplexe, Größen beschrieben die durch Kurzschlüsse und Leerläufe an Ein- und Ausgang ermittelt werden
Können. In der Vorlesung wurden die h-, y- und π-Parameter vorgestellt.
2. Physikalische Ersatzschaltbilder: In denen wird versucht, die physikalischen Vorgänge im Transistor
durch Schaltungselemente nachzubilden. Sie unterteilen sich wiederum in:
TU-Berlin
8/10
Mönich/Zinal
Schaltungstechnik
2.Übung
SS2009
2. (a) Allgemeine bzw. vollständige Ersatzschaltbilder:
E’
U
r
Id
g
e’b’
r
c
g
r
c
g
Id
C’
C’
1
U
ku
c’b’
c
I
d
U
c’b’
B’
B’
B’
r
B’
b
Die obige Abb. zeigt ein ESB in dem die Vorgänge im inneren Transistor modelliert werden. Der
Kettenleiter aus den Elementen g, c und r soll den Diffusionsvorgang der Ladungsträger durch die
Basiszone darstellen. Dabei geben die Admittanzen z.B. die Wirkung der Rekombination wieder.
Die gesteuerte Spannungsquelle soll die Rückwirkung des Ausgangskreises auf den Eingangskreis
wiedergeben, welche hauptsächlich durch die Basisweitenatmung (Early-Effekt) verursacht wird.
Die nachfolgende Abb. zeigt ein vollständiges physikalisches ESB:
c
E
r
ee’
ec
C’
E’
ku r
g
g
ed
c
d
ku l
d
cc’
C
(ku−1)U e’b’
c
ed
B’
es
r
g
cd
cd
gcs
c eb
c cb
c es
r
bb’
c
cs
B
Dabei sind:
rbb0 , ree0 , rcc0 die Bahnwiderstände von Basis, Emitter und Kollektor.
cec , ceb , ccb die Kapazitäten zwischen den Äußeren Anschlüssen E, B und C einschließlich der vom
Gehäuseaufbau verursachten Kapazitäten.
ces , ccs Sperrschichtkapazitäten.
ced , ccd Diffusionskapazitäten.
ged , gcd Leitwerte von Emitter- und Kollektorsperrschicht.
1/ku Steuerfaktor des inneren Transistors.
TU-Berlin
9/10
Mönich/Zinal
Schaltungstechnik
2.Übung
SS2009
2. (b) Praktische Ersatzschaltbilder: Diese gehen von dem vollständigen ESB aus, verzichten jedoch
auf Schaltungselemente die abhängig von Frequenzbereich, Schaltungsart oder Aufbau des Transistors vernachlässigt werden können. Die wichtigsten praktischen Ersatzschaltbilder sind:
i. ESB nach Zawels: Dieses ESB ist bis zur α-Grenzfrequenz gültig (f ≤ fα ).
C
E
ku r
g
c
e
d
ku l
d
(ku−1)U eb’
c
e
g
c
c
B’
r
b
c
B
a
ii. ESB nach Early (f ≤ 0.1 fα ):
r*
r*
b
E
b
B’
C
Ie
Ic
µ Ucb
c*e
r
αIe
b2
U eb
U cb
c*
c ges
r
b1
B
B
iii. ESB nach Giacoletto ((f < fα ):
g
B
B’
r
~
U
c
C
C
bb’
~
U
be
b’e
g
C
e
c
g
e
~
SU
ce
~
U
b’e
ce
E
iv. ESB nach Pritchard (f ≤ 2 fβ ):
g
B
B’
r
~
U
be
c
C
C
bb’
~
U
b’e
g
C
e
g
c
1
g
e
~
βI
0 b
2
~
U
ce
C1
E
Die α-Grenzfrequenz ist diejenige, bei der die Kurzschlußstromverstärkung der Basisschaltung
α = IIEC um 3dB gesunken ist.
Die β-Grenzfrequenz ist diejenige, bei der die Kurzschlußstromverstärkung der Emitterschaltung
β = IIBC um 3dB gesunken ist.
TU-Berlin
10/10
Mönich/Zinal