Experimentelle Analyse von realen Spannungsquellen
Werbung

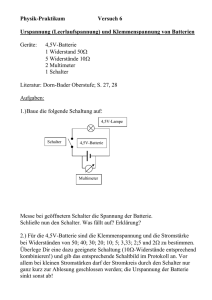
3. Klasse - NW Woche 2012 - MD Experimentelle Analyse von realen Spannungsquellen 1 Einleitung In diesem Projekt lernt ihr die Grundlagen von Solarzellen kennen. In unterschiedlichen Praktika experimentiert ihr selbständig mit realen Spannungsquellen, kommerziellen und selbst gebastelten Solarzellen, ihr erfasst Daten, versucht sie mit einer mathematischen Funktion zu beschreiben und interpretiert die Parameter nach einer passenden physikalischen Theorie. Damit alles erreicht wird, musst ihr zuerst die Grundlagen der realen Spannungsquelle und der Datenanalyse kennenlernen. Dies wird auch im kommenden Praktikum (Frühingssemester) sehr nützlich sein. 2 Wie geht ihr vor? Die Idee ist, dass ihr heute Nachmittag selbständig in Zweiergruppen arbeitet. Die Aufgaben a) - n) werdet ihr in eine Excel-Datei lösen (Bitte die Lösungen mit a, b, c, bezeichnen), welche ihr am Ende dieses Leitprogramms einem Leiter schickt/gibt ([email protected] oder [email protected]). Falls wir sie in Ordnung finden, seid ihr für heute fertig. Der Theorieteil ist eigentlich eine Repetition des im Physikunterricht behandelten Stoffs. Beim praktischen Teil hingegen lernt ihr mit Multimeter, Spannungsquellen, Kabel und Widerständen umzugehen (keine Angst, es ist nicht gefährlich). Anschliessend wird euch erklärt, wie man Messwerten graphisch mit Excel (oder ähnlichem) auswertet. Natürlich stehen wir immer zur Verfügung und helfen ihr bei Fragen sehr gern weiter. 3 Ideale Spannungsquellen Jeder Stromkreis besteht im Prinzip aus einer Spamnungsquelle U0 - wir nehmen hier an, es handle sich um eine Batterie aber sehr ähnlich verhält sich ein Solarpanel oder ein Windrad - und einem Verbraucher, der allgemein als elektrischer Widerstand R dargestellt werden kann. Der Strom, der vom Pluspol zum Minuspol der Batterie fliesst, gehorcht näherungsweise dem Ohmschen Gesetz I0 = UR0 . Wenn U0 immer gleich bleibt, bedeutet dies, dass für kleiner werdende R ein immer grösser Strom fliesst. Und bei einem Kurzschluss - d.h. R = 0 Ω, nur noch der fast widerstandsfreie Draht liegt zwischen den Polen der Batterie - wird der Strom unendlich gross. Wir wollen dies anhand der untenstehende Schaltung überprüfen. Achtung: diese Messung belastet die Batterie stark und kann bei falscher Bereichswahl das Multimeter beschädigen! a) Nimm zwei Kabel, eine ”neue” und eine ”leere” 4.5 V-Batterie, das gelbe Multimeter und schalte es auf den Spannungsmessebereich V̄ ein (d.h. Gleichspannung, DC sollte auf dem Bildschirm erscheinen). Bei allen Multimeter muss ein Kabel mit ”COM” eingeschlossen werden. Uns interessiert zuerst die Spannung, also das zweite Kabel mit V̄ anschliessen. Die beiden anderen Enden der Kabel könnt ihr jetzt mit den Plus- und Minuspol der Batterie anschliessen. Notiere die (Ur- oder Leerlauf-) Spannung U0 beider Batterien, mit Fehlerschranke (siehe nächsten Abschnitt, das Vorzeichnen ist nicht wichtig und hängt von der Stromrichtung ab). Hinweis: Wie schätzt man eine Fehlerschranke ab? Man schaut welche Ziffer bei der Messung unsicher ist, d.h. sich kontinuierlich ändert. Als Fehler nimmt man die Hälfte dieser Ziffer. Bsp: Gemessene Spannung 3.92 V, wobei die letzte Ziffer zwischen 2 und 3 wechselt: als Fehlerschranke wird mindestens die Hälfte von 0.01 V genommen, also 0.005 V. b) Wähle jetzt den Strommessbereich I¯ (d.h. Gleichstrom, DC sollte auf dem Bildschirm erscheinen). Ein Kabel schliesst ihr wie immer mit ”COM” an, das zweite mit dem grössten Strommessbereich (10 A?) an. Schliesse jetzt die Batterie nur für 1-2 Sekunden an. Notiere den Kurzschlusstrom I0 mit Fehlerschranke. Während die elektrische Spannung U0 für die ”neue” Batterie im Bereich 4-4.5 V ist (und für die ”leere” deutlich tiefer), wird der Strom I0 beim Kurschliessen der Pole nicht unendlich gross. Warum? Kann es daran liegen, dass wir den Kabelwiderstand nicht berücksichtigt haben? Testen wir das! c) Schalte das Multimeter auf den Widerstandsbereich Ω ein. Schliesse ein Kabel mit ”COM”, das andere mit Ω und die freien Enden miteinander an. Notiere den Widerstand mit Fehlerschranke. Welcher Strom müsste fliessen, wenn nur der Kabelwiderstand da wäre? (Hinweis: Ohmsches Gesetz!) Der Widerstand der Kabel reicht offensichtlich nicht, um den Strom auf den gemessenen Wert zu begrenzen. Es muss in der Batterie selbst ein Widerstand vorhanden sein, der Innenwiderstand Ri , welcher den Kurzschlussstrom automatisch begrenzt. Genau das Gleiche passiert bei Windrädern und Solarzellen, wie ihr sehen werdet, was einen grossen Einfluss auf die Effizienz von Erneuerbaren Energiequellen hat. 4 Modell einer realen Spannungsquelle Reale Spannungsquellen kann man elektrisch mit dem nebenstehenden Schema beschreiben. Die Batterie besteht nach diesem Modell aus einer idealen Spannungsquelle mit Urspannung oder Leerlaufspannung U0 , deren Wert immer gleich bleibt, und einem Innenwiderstand Ri . K+ und K− sind die Klemmen der Batterie. Die Spannung, die an den Klemmen der Batterie gemessen wird, wird Klemmenspannung Uk genannt und ist kleiner als die Urspannung U0 , weil ein Teil der von der idealen Batterie freigesetzten Energie vom Innenwiderstand gebraucht wird. Bei jeder realen Spannungsquelle, sei diese eine Batterie oder ein Solarpanel, ist der Innenwiderstand Ri immer dabei und hängt von den chemischen Reaktionen ab, die den Ladungstransport durch Ionen ermöglichen. Diesen können wir nicht umgehen, da wir nur Zugang zu den Klemmen K+ und K− haben. Um die Leistung und den Wirkungsgrad einer erneuerbaren Energiequelle zu untersuchen, müssen wir zuerst lernen, wie man den Innenwiderstand einer realen Energiequelle experimentell bestimmt und was er bedeutet. 5 Mathematische Darstellung des Innenwiderstands einer Batterie Wird eine Spannungsquelle eingesetzt um einen Verbraucher zu betreiben, so hat der Innenwiderstand einen Einfluss auf das Geschehen im ganzen Stromkreis. Die Situation ist im folgenden Schema dargestellt: Die Batterie (oder das Solarpanel) wird an einen Lastwiderstand RL (Verbraucher) angeschlossen. Der Innenwiderstand wird wie ein zusätzlicher in Serie zu RL geschalteter Widerstand behandelt. Mit Voltmeter V und Amperemeter A können Klemmenspannung Uk und Stom I gemessen werden. - Wenn die Spannungsquelle nicht belastet wird, d.h. wenn kein Strom fliesst, absorbiert der Innenwiderstand keine Energie und die Klemmenspannung Uk ist gleich der Urspannung U0 . Dies passiert zum Beispiel, wenn man die Klemmenspannung mit dem Voltmeter ohne Verbraucher misst (der Widerstand des Voltmeters ist so gross, dass kein Strom fliesst). - Wenn an die Batterie nun ein Lämpchen oder ein Motor mit Widerstand RL betrieben wird (Lastwiderstand RL ), ist die mit dem Voltmeter gemessene Klemmenspannung Uk kleiner als die Urspannung U0 : es fliesst jetzt ein Strom durch den Lastwiderstand und den Innenwiderstand, welcher einen Teil der von der idealen Quelle freigesetzten Energie absorbiert. Natürlich hängt der Strom von RL ab: ist er gross, so ist I klein. Ist RL im Gegenteil klein, so ist I gross. Mathematisch sieht dies für einen Ohmschen (d.h. konstanten) Innenwiderstand wie folgt aus: U0 = Rtot · I = (Ri + RL ) · I = Ri · I + RL · I = Ri · I + Uk mit RL · I = U k , weil der Innenwiderstand Ri in Serie mit dem Lastwiderstand RL ist und die Spannung Uk im Verbraucher benutzt wird. Gelöst nach dem Strom erhalten wir dann: I= U0 −Uk Ri = U0 Ri − Uk Ri =⇒ I = − R1i · Uk + U0 Ri Diese ist eine lineare Funktion der Art y = −m · x + q und ihr Diagramm, ”Strom in Funktion der Klemmenspannung”, wird Kennlinie I(U ) genannt und ist wie der ”Pass” einer Spannungsquelle (Achtung: nicht alle Kennlinien sind lineare Funktionen). Aus der Kennlinie kann man zum Beispiel den Innenwiderstand, die maximale Leistung und die Effizienz herausfinden! 6 Experimentelle Bestimmung der Kennlinie einer Batterie Um die Eigenschaften einer Spannungsquelle experimentell zu untersuchen, musst ihr nun die oben erwähnte Schaltung bauen, damit ihr Klemmspannung Uk und Strom I bei unterschiedlichen Lastwiderständen messen und daraus die Kennlinie I(Uk ) graphisch darstellen könnt. d) Material: wieder eine ”neue” und eine ”leere” 4.5 V-Batterie, 1 gelbes Multimeter (für den Strom) und ein grünes Multimeter (für die Spannung), ein variabler Widerstand (max 100 Ω), verschiedene Kabel und ein Schalter. Bitte lässt ihr die Schaltung von einer Lehrperson kontrollieren, bevor ihr zum Punkt e) weitergeht. Hinweise: - Wie ihr im Physikunterricht gelernt habt, wird ein Amperemeter in Reihe (alle pro Sekunde fliessende Ladungsträger müssen gezählt werden) und ein Voltmeter in parallel geschaltet (Spannung ist die Differenz zweier Energiezustände pro Ladungsmenge). - Der variable Widerstand hat drei Eingänge: damit er als variabel funktioniert, den linken und den mittleren (rote) Eingang benutzen. Durch Drehen des Stellards wird RL geändert, bis maximal 100 Ω (in Uhrzeigersinn wird erhöht). - Um die Batterie zu schonen wird zwischen der Spannungsquelle und dem Lastwiderstand ein Schalter eingesetzt. Er hat zwei Positionen: in einer lässt er den Strom durch und in der zweiten wird die Schaltung unterbrochen. e) Wenn ihr das OK vom Lehrer habt, geht es los: misst fünfzehn Mal Strom und Spannung bei unterschiedlichem Lastwiderstand für die ”neue” und die ”leere” Batterie. Am besten sind die Wertepaare schön verteilt. Vor allem bei grossen Stromwerten den Schalter nur kurzzeitig einschalten (2-3 s), Werte ablesen und wieder abschalten. Die Batterie ermüdet sich rasch, was die Messung verfälscht. Falls nötig stehen weitere kleineren RL zur Verfügung, damit die Messung bei kleineren Lastwiderständen einfacher wird. Es reicht wenn ihre Messungen 2 signifikante Ziffer haben. Notiere auch eine Fehlerschranke für I und Uk jeweils (Fehler bei der dritten Stelle). 7 Auswertung der Messdaten Für die folgende graphische Analyse stehen für Excel/Openoffice verschiedene Tutorials zur Verfügung: http://ta.perihel.ch/Material/Theorie/Grundlagen/tutorial_excel/Fehlerbalken.html http://lie.perihel.ch/Praktikum/Tutorials/Regression_Excel/ http://lie.perihel.ch/Praktikum/Tutorials/Diagramme_in_Excel/ Falls ihr mit Numbers (apple) arbeitet, werden die Diagramme ähnlich wie oben gezeichnet und deren Eigenschaften mit Settings (oben-rechts) gesteuert (sehr user-friendly). Bei Fragen helfen wir euch gern weiter! f ) Tippe alle Werte in eine Excel-Tabelle ein (erste Kolonne Uk in Volt V, zweite Kolonne I in Ampere A), sowohl für die ”neue” als auch für die ”leere” Batterie. Zeichne die Kennlinie, also das I(Uk )-Diagramm in beiden Fällen (am besten ins gleiche Diagramm). Es müssen nur die Wertepaare (Un , In ) gezeichnet werden, ohne Verbindungslinie (Dispersionsdiagramm). g) Füge die Fehlerbalken für Uk und I bei euren Messwerten ein. (Zwischendurch speichern) h) Füge die Trendline bei beiden Kennlinien ein. Lasse die Software die Funktion zeigen (3 signifikante Ziffer sind genug). Die Trendlinie soll durch die Fehlerbalken aller Wertepaare gehen. Falls dies nicht der Fall ist, sind die Fehlerschranken wahrscheinlich zu klein. i) Vergleiche die Trendlinie mit der mathematischen Funktion I(Uk ), ”Strom in Funktion der Klemmenspannung”. Welche Einheiten und Bedeutung haben die Parameter der Trendlinie? Finde daraus die Urspannung U0 , den Innenwiderstand Ri und den Kurzschlussstrom I0 der zwei Batterien. Vergleiche die Resultate der ”neuen” und der ”leeren” Batterie und mit den in a) und b) gemessenen Werten. Was macht eine ”leere” Batterie ”leer” und eine ”neue” ”geladen”? j) Die Leistung P eines Lastwiderstandes, d.h. die nutzbare Leistung, kann man herausfinden, in dem man Strom und Klemmspannung zusammenmultipliziert: P = I · Uk Füge eine Kolonne neben dem Strom ein, rechne die Leistung (nur) für die ”neue” Batterie aus und zeichne in ein neues Diagramm die Wertepaare (Pn , Un ). Füge die Fehlerbalken für Uk und P ein (für P kannst du die gleiche Grössenordnung nehmen, wie bei Uk ). k) Füge eine Trendlinie ein: die Punkten liegen jetzt nicht auf einer geraden, sondern scheinbar auf einer Parabel. Wähle also ein Polynom zweiter Ordnung! Lasse ddie Software die Funktion zeigen (3 signifikante Ziffer sind genug). Geht die Trendlinie durch die Fehlerbalken aller Wertepaare? m) Welche Einheiten und welche welche Einheit haben die Parameter der Trendlinie? Hinweis: was passiert wenn ihr bei P = I · Uk für I die Funktion I(Uk ) einsetzt? Finde daraus den Innenwiderstand, die Urspannung und den Kurzschlussstrom und vergleiche die Resultate mit denen von i). Betrachte auch die Fehlerschranke. n) Wie gross ist die Maximale Leistung? Bei welcher Spannung gibt sie die Batterie ab? Wie gross muss der ab hat sie Lastwiderstand sein, damit die Batterie die maximale Leistung abgibt? Welchen Wirkungsgrad η = PPtot dann? Wo wird der Rest verbraucht? 8 Abschluss Benenne eure Excel-datei Name1_Name2.xls und sende diese an die Kursleiter ([email protected] oder [email protected] oder komme mit einem Datenträger vorbei). Ihr seid erst dann fertig, wenn eure Arbeit kontrolliert und für gut befunden worden ist. Dazu musst ihr persönlich bei den Kursleitern vorbeigehen.