2. Tag 550734 Lösung 6 Punkte Teil a) Klasse 7a

55. Mathematik-Olympiade
3. Stufe (Landesrunde)
Olympiadeklasse 7
Lösungen – 2. Tag
c 2015 Aufgabenausschuss des Mathematik-Olympiaden e.V.
www.mathematik-olympiaden.de. Alle Rechte vorbehalten.
550734 Lösung
6 Punkte
Teil a) Klasse 7a bietet (50 + 400 = ) 450 Lose an; 50 Lose gewinnen. Die Gewinnchancen für
das zuerst gezogene Los betragen daher (50 : 450 = ) 91 . Da 12,5 % einem Achtel entsprechen,
sind in Klasse 7b die Gewinnchancen für das zuerst gezogene Los 18 . Wegen 19 < 18 sind in
Klasse 7b die Gewinnchancen für das zuerst gezogene Los größer.
Teil b) Da Markus als Erster die Lose zieht, sind noch alle 400 Nieten in der Lostrommel.
Er müsste also mindestens 401 Lose kaufen, um sicher ein Gewinnlos zu ziehen.
Teil c) 1. Möglichkeit: Die Klasse 7a entfernt 50 Nieten. Dann betragen die Gewinnchancen
für das zuerst gezogene Los (50 : (450 − 50) = 50 : 400 = ) 18 . Die gleiche Chancenverteilung
wurde in Teil a) bei Klasse 7b ermittelt.
2. Möglichkeit: Bei der Klasse 7b sind 12,5 % der 320 Lose Gewinnlose. Sie hat also 40 Gewinnlose. Die Klasse 7b fügt 40 Nieten hinzu. Dann betragen nunmehr die Gewinnchancen
für das zuerst gezogene Los (40 : (320 + 40) = 40 : 360 = ) 91 . Die gleiche Chancenverteilung
wurde in Teil a) bei Klasse 7a festgestellt.
Lösungsvariante zu Teil c): Diese Lösungsvariante zeigt einen möglichen Gedankengang für
die Ermittlung der gesuchten Zahlen; eine derartige Herleitung wird aber in dieser Aufgabe
vom Schüler nicht verlangt.
Eine Möglichkeit ergibt sich, wenn die Klasse 7a die Anzahl ihrer Nieten so verringert, dass die
Gewinnchance für das erste Los genau so groß ist wie in der Klasse 7b. Es sei na die Anzahl
der zu entfernenden Nieten in der Klasse 7a. Dann gilt
1
50
=
450 − na
8
und folglich na = 50. Die gleiche Gewinnchance wird also erreicht, indem die Klasse 7a von
ihren 450 Losen 50 Nieten entfernt.
Eine andere Möglichkeit ergibt sich, wenn die Klasse 7b die Anzahl ihrer Nieten so erhöht,
dass die Gewinnchance für das erste Los genau so groß ist wie in der Klasse 7a. Bei der Klasse
7b sind 12,5 % der 320 Lose Gewinnlose. Sie hat also 40 Gewinnlose. Es sei nb die Anzahl der
hinzugefügten Nieten in der Klasse 7b. Dann gilt
40
1
=
320 + nb
9
und folglich nb = 40. Die gleiche Gewinnchance wird also erreicht, indem die Klasse 7b zu
ihren 320 Losen 40 Nieten hinzugibt.
5
550735 Lösung
7 Punkte
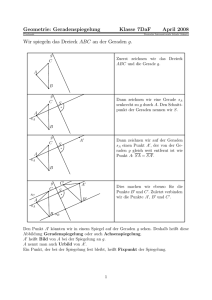
Wir bezeichnen den Mittelpunkt der Strecke AB mit M . Nach Voraussetzung gilt dann
1
· |AB| = |AM | = |BM | = |BC| = |CD| = |AD| .
2
(1)
D
gelten, siehe Abbildung L 550735 a.
Wegen (1) ist das Dreieck AM D gleichschenklig
mit der Basis M D. Nach dem Basiswinkelsatz gilt
daher
A
C
||
M
||
S
||
(2)
AB k CD
||
Da das Viereck ABCD nach Voraussetzung ein
Trapez ist, sind zwei seiner Seiten parallel zueinander. Wegen (1) kann nur
||
B
L 550735 a
(3)
|ADM | = |DM A| .
Wegen (2) und nach dem Wechselwinkelsatz angewandt auf die Parallelen AB und CD folgt
(4)
|M DC| = |DM A| .
Aus (1), (3) und (4) folgt
|AD| = |CD| ,
|ADM | = |M DC| .
Hieraus folgt, dass eine Spiegelung an der Geraden DM den Punkt A auf den Punkt C und
den Punkt C auf den Punkt A abbildet, also die Gerade AC auf sich. Folglich steht die Gerade
AC senkrecht auf der Spiegelachse DM ,
(5)
DM ⊥ AC .
Aus (1) und (5) folgt, dass die Gerade AC eine Spiegelachse des Dreiecks AM D ist und dass
daher der Punkt M Spiegelpunkt von D bei der Spiegelung des Dreiecks ACD an der Geraden
AC ist. Hieraus folgt, dass die Strecke CD bei Spiegelung an der Geraden AC auf die Strecke
CM abgebildet wird. Daher gilt
(6)
|CM | = |CD| .
Ebenso lässt sich mit Hilfe der beiden gleichschenkligen Dreiecke M BC und BCD zeigen, dass
M Spiegelpunkt von C bei Spiegelung an der Geraden BD ist. Daher gilt
(7)
|DM | = |CD| .
Aus (1), (6) und (7) folgt
|CM | = |DM | = |AM | = |BM | = |BC| = |CD| = |AD| .
(8)
Aus (8) folgt nun, dass die Dreiecke AM D und M BC gleichseitig sind und jeder ihrer Innenwinkel somit die Größe 60◦ hat. Weiter folgt aus (8), dass jedes der beiden Vierecke AM CD
und M BCD ein Rhombus ist und da in einem Rhombus die Diagonalen Winkelhalbierende
sind, gilt |BAS| = |SBA| = 30◦. Hieraus und nach dem Innenwinkelsatz angewandt auf
das Dreieck ABS folgt |ASB| = 180◦ − 2 · 30◦ = 120◦.
Der Winkel ASB ist also 120◦ groß.
6
1. Lösungsvariante: Wie in der Lösung schließen
D
C
wir zuerst auf (1) und (2). Wegen (2) gilt nach
dem Wechselwinkelsatz |M AC| = |DCA|.
Wegen (1) ist das Dreieck ACD gleichschenkS
lig. Nach dem Basiswinkelsatz folgt |CAD| =
|DCA|. Hieraus und aus |M AC| = |DCA|
||
||
folgt |M AC| = |CAD|. Die Spiegelung an der
A
B
M
Geraden AC bildet daher den Schenkel AD auf
den Schenkel AM ab, wobei wegen (1) der Punkt
L 550735 b
D auf den Punkt M abgebildet wird. Folglich bildet diese Geradenspiegelung die Strecke CD auf die Strecke CM ab, woraus |CD| = |CM | und
|DCA| = |ACM | folgen. Mit den entsprechenden Überlegungen für das Dreieck BCD in
Bezug auf die Spiegelung an der Geraden BD folgen |CD| = |DM | und |M DB| = |BDC|.
Das Dreieck CDM ist folglich gleichseitig und die Geraden AC und BD sind zwei seiner drei
einander im Punkt S schneidenden Innenwinkelhalbierenden, siehe Abbildung L 550735 b. Da
die Innenwinkelhalbierenden im gleichseitigen Dreieck den Vollwinkel um ihren Schnittpunkt
in 6 gleich große Winkel zerteilen, gilt |DSA| = 60◦ und nach dem Nebenwinkelsatz daher
|ASB| = 120◦.
||
||
||
2. Lösungsvariante: Wie in der Lösung schließen wir zuerst auf (1) und (2). Aus (1) folgt
|AM | = |CD|. Wegen (2) und nach dem Wechselwinkelsatz folgt |DM A| = |M DC|. Zudem
haben die Dreiecke AM D und CDM die Seite DM gemeinsam. Nach dem Kongruenzsatz
(sws) folgt die Kongruenz der Dreiecke AM D und CDM , woraus |CM | = |AD| = |CD|
folgt. (Diese Beziehung kann auch durch Betrachtung der Punktspiegelung am Mittelpunkt
der Strecke DM gezeigt werden.) Das Viereck AM CD ist folglich ein Rhombus. Mit den
entsprechenden Überlegungen folgt, dass auch BCDM ein Rhombus ist. Die Geraden AC
und BD sind daher Winkelhalbierende der Winkel DCM bzw. M DC. Wie in der Lösung
oder der Lösungsvariante folgt |ASB| = 120◦.
550736 Lösung
7 Punkte
I. Es sei z eine durch 9 teilbare dreistellige positive ganze Zahl, die bei Addition von 594 eine
dreistellige Zahl mit umgekehrter Ziffernfolge ergibt. Dann lässt sich z darstellen durch
(1)
z = 100a + 10b + c
mit
a, b, c ∈ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ,
a 6= 0 ,
c 6= 0 ,
(2)
wobei nach Voraussetzung
(3)
100a + 10b + c + 594 = 100c + 10b + a
gilt.
Durch Umformen von Gleichung (3) folgt 99c − 99a = 594, c − a = 6 und schließlich
(4)
c = a + 6.
Wegen (2) kommen für a nur die Zahlen 1 oder 2 oder 3 infrage.
Da z nach Voraussetzung durch 9 teilbar sein soll, muss die Quersumme a + b + c von z durch
9 teilbar sein. Wegen (2) gilt 2 ≤ a + b + c. Wegen (2) und (4) gilt a ≤ 3. Hieraus und wegen
7
(2) folgt 2 ≤ a + b + c ≤ 21. Daher muss
a + b + c = 9 oder a + b + c = 18
(5)
gelten.
Aus (4), (5), (1) und a = 1 folgen c = 7, b = 1 und z = 117.
Aus (4), (5), (1) und a = 2 folgen c = 8, b = 8 und z = 288.
Aus (4), (5), (1) und a = 3 folgen c = 9, b = 6 und z = 369.
Wenn eine Zahl die Forderungen des Aufgabentextes erfüllt, kann dies also nur eine der Zahlen
117, 288 und 369 sein.
II. Tatsächlich gilt für die Zahlen 117, 288 und 369:
– Die genannten Zahlen sind dreistellige positive ganze Zahlen.
– Wegen 117 : 9 = 13, 288 : 9 = 32, 369 : 9 = 41 sind sie durch 9 teilbar.
– Jede von ihnen ergibt bei Addition von 594 die Zahl mit der jeweils umgekehrten Ziffernfolge: 117 + 594 = 711, 288 + 594 = 882, 369 + 594 = 963.
Aus I. und II. folgt: Die zu ermittelnden Zahlen sind 117, 288 und 369.
8
Punktverteilungsvorschläge
Die nachstehenden Angaben zur Punktverteilung sowohl für die gesamten Aufgaben als auch
für die Teillösungen sind Empfehlungen für die Ausrichter des Wettbewerbs und sollen einer
einheitlichen Bewertung dienen. Dies vereinfacht für die Schülerinnen und Schüler ein Nachvollziehen der Bewertung und ermöglicht für die Organisatoren Vergleiche zum Zweck der
Entscheidung über die Teilnahme an der nächsten Runde.
Bei der Vielfalt der Lösungsvarianten ist es nicht möglich, Vorgaben für jede Variante zu
machen; das Korrekturteam möge aus den Vorschlägen ableiten, welche Vergabe dem in der
Schülerlösung gewählten Ansatz angemessen ist. Dabei können auch Lösungsansätze, die angesichts der Aufgabenstellung sinnvoll erscheinen, aber noch nicht erkennen lassen, ob sie
wirklich zu einer Lösung führen, einige Punkte erhalten.
Abweichungen von den Vorschlägen müssen von den Ausrichtern des Wettbewerbs ausreichend bekannt gemacht werden. Es wird aber empfohlen, zumindest den prozentualen Anteil
der Punkte für Teillösungen beizubehalten.
Aufgabe 550734
Insgesamt: 6 Punkte
Teil a) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Punkte
Teil b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Punkte
Teil c) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 Punkte
Aufgabe 550735
Insgesamt: 7 Punkte
Es ist eine brauchbare Lösungsidee erkennbar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Angabe aller zur Ermittlung erforderlichen Feststellungen . . . . . . . . . . . . . . . . . . . . . . . .
Zugehörige Begründungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Angabe der richtigen Winkelgröße . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Aufgabe 550736
1
2
3
1
Punkt
Punkte
Punkte
Punkt
Insgesamt: 7 Punkte
Nutzung einer prinzipiell geeigneten Lösungsstrategie . . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Korrekte und vollständige Herleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Probe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . .
Ergebnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1
4
1
1
Punkt
Punkte
Punkt
Punkt