Document
Werbung
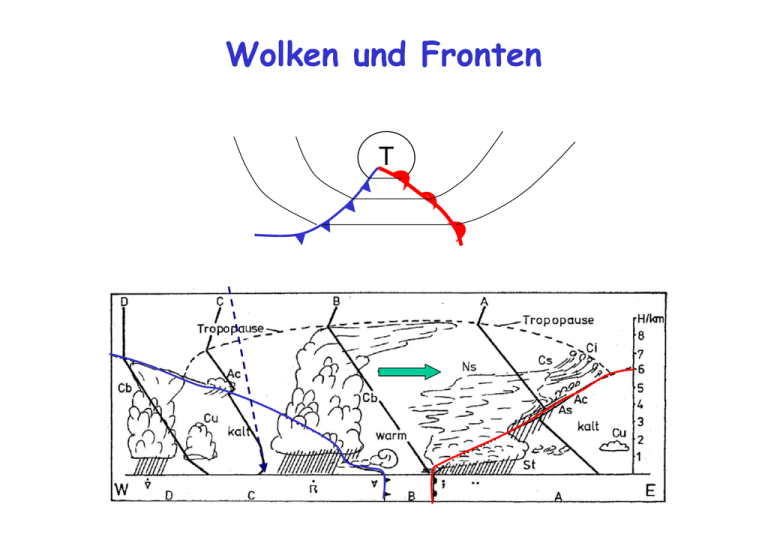
Wolken und Fronten T 1 Lerninhalte 8. Vorlesung Was sind Squall lines? Was passiert bei der Tornadobildung? Wie ist das elektrische Feld der Atmosphäre? Was passiert bei Blitzen? Was ist das elektromagnetische Spektrum? Welche Strahlungsquellen sind für die Atmosphäre relevant? Was ist die Bedeutung der Strahlung für die Atmosphäre? 2 Tornado Wind Patterns 3 Gliederung der Vorlesung 1. 17.10.2005 Aerosole - Definition, Quellen und Senken, Größenverteilung 2. 24.10.2005 Auswirkungen Aerosol, Wolkenbildung - Sättigung 3. 31.10.2005 Entstehung von warmen Niederschlag 4. 7.11.2005 5. 14.11.2005 Radarmeteorologie Niederschlag 6. 21.11.2005 Wolkenbildung, Wolkentypen, Wolkendynamik 7. 28.11.2005 Luftmassengewitter 8. 5.12.2005 9. 12.12.2005 Strahlung und Strahlungsgesetze Entstehung von kaltem Niederschlag Gewittertypen 10. 19.12.2005 Streuung in der Atmosphäre, optische Erscheinungen 11. 9.1.2006 Globale Strahlungsbilanz 12. 16.1.2006 Anthropogener Treibhauseffekt/Klimaänderungen 13. 23.1.2006 Stratosphärischer Ozonabbau 14. 30.1.2006 Allgemeine Zirkulation 15. 6.2.2006 Hydrologischer Kreislauf 4 Gliederung der Strahlung Meteorologisch wirksame Strahlung - Bedeutung der Strahlung für die Atmosphäre - planetare Albedo, Energiehaushalt - Absorption/Emission durch Atome und Moleküle - Beschreibung elektromagnetischer Wellen (Strahlungsintensitätsmaße) - Raumwinkel Strahlungsgesetze - spektrale Einheiten - Planck-Gesetz (Rayleigh-Jeans-Gesetz) - Wien'sches Verschiebungsgesetz - Stefan-Boltzmann-Gesetz - Kirchhoff-Gesetz Solare und terrestrische Strahlung Phänomenologie der Strahlungsflüsse Optische Erscheinungen in der Atmosphäre 5 Test vom Oktober 4.) Welche Strahlungsgesetze kennen Sie und was beschreiben diese? - Stefan-Boltzmann-Gesetz - Wien'sches Verschiebungsgesetz - Kirchhoff'sches Gesetz - Planck Keine Antwort II 5) Welche Partikel streuen elektromagnetische Strahlung in der Atmosphäre? Moleküle: O3,FCKW,H2O,CO2,CO Proton, Elektron, Ionen Aerosole, Wolken Wellenlängenabhängigkeit Keine Antwort IIIII IIIII I 6 Elektromagnetisches Spektrum cVakuum ≈ c Luft = λ ⋅ν = 2.99793 ⋅10 8 m / s 7 Bedeutung der Strahlung Energieaustausch zwischen Weltraum, Atmosphäre und Erdoberfläche Energieaustausch zwischen den verschiedenen Schichten der Atmosphäre Wichtige chemische Reaktionen in der Atmosphäre laufen nur ab, wenn elektromagnetische Strahlung bestimmter Wellenlänge vorhanden ist, z.B. O2 + hν → O + O λ < 240 nm - Ozonbildung in der Stratosphäre - Photosynthese Optische Erscheinungen - Himmelsblau - Sichtweite - Erscheinung von Wolken Fernerkundung (remote sensing) atmosphärischer Bestandteile (Wolken, Temperatur, Feuchte...) 8 Planetare Albedo Prozentualler Anteil der in den Weltraum zurückreflektierten solaren Einstrahlung Erdalbedo ist ca. 30% = (19 + 6 + 5) 9 Energiehaushalt Erde-Atmosphäre Atmosphere Energy Balance 10 Absorption und Emission von Strahlung durch Moleküle Jedes einzelne Molekül besitzt eine bestimmte Energie, abgesehen von der Energie, die mit der Bewegung des Moleküls verbunden ist. Die kinetische und elektrostatische potentielle Energie der Elektronen, die um die Atomkerne kreisen, hat den größten Anteil. Einen geringen Beitrag zur Gesamtenergie liefern - die Schwingungen der einzelnen Atome im Molekül um deren Mittellagen, - die Rotation des Moleküls um den Schwerpunkt. In der Quantenmechanik wird gezeigt, daß: - nur bestimmte Elektronenbahnen um die Atomkerne - nur bestimmte Schwingungsfrequenzen und –amplituden - nur bestimmte Rotationsgeschwindigkeiten für die Moleküle erlaubt sind. Jede mögliche Kombination aus Elektronenbahnen, Schwingung und Rotation kann mit einem bestimmten Energieniveau in Verbindung gebracht werden. Dieses Energieniveau entspricht der Summe drei Energiearten. 11 Absorption und Emission von Strahlung durch Moleküle Durch Absorption bzw. Emission von elektromagnetischer Strahlung kann das Molekül zu einem höheren bzw. niedrigeren Energieniveau übergehen. Nach der Quantenmechanik sind nur diskrete Änderungen Energie erlaubt. Die Energieänderungen sind bei Absorption und Emission gleich groß. E E = h ⋅ν = h c λ 12 Verschiedene Moleküle Ein einzelnes Molekül kann nur diskrete Energiemengen absorbieren, bzw. emittieren. Deshalb kann es auch nur mit Strahlung bestimmter, diskreter Wellenlängen wechselwirken: Linienspektrum eines Gases Diese Absorptions-(Emissions-)linien haben eine bestimmte Breite aufgrund der Unschärferelation*, Druck- und Dopplerverbreiterung Flüssigkeiten und Festkörper haben Bandenspektren Absorption und Emission findet wegen der starken Wechselwirkungen zwischen den Kräftefeldern der einzelnen Moleküle über einen kontinuierlichen Wellenlängenspektrum statt. Auch bei mehratomigen Gasen beobachtet man Absorptions -bzw. Emissions-Banden, die jedoch die Wellenlängenbereiche nicht kontinuierlich überdecken, sondern eine Gruppe von sehr vielen Spektrallinien sind. *nach Heisenberg ist es unmöglich, Ort und Geschwindigkeit eines Teilchens gleichzeitig zu bestimmen 13 Verschiedene Moleküle Für den Strahlungshaushalt des Systems Erde-Atmosphäre sind die Absorptions- bzw. Emissionsbanden der Gase, H2O, CO2, und O3 sehr wichtig. Die O2- und N2-Moleküle können nicht auf diese Weise mit der Strahlung wechselwirken, so daß sie im solaren und terrestrischen Wellenlängenbereich nicht relevant sind (z.B. O2 + hν → O+ O für λ<240 nm) Das Wassermolekül besteht aus drei Atomen (N=3) und hat somit 3 Schwingungsfreiheitsgrade und drei klassische Frequenzen ν1, die den Wellenlängen λ1, λ2 und λ3 entsprechen. Es gibt Kombinations- und Obserschwingungen. 14 Beschreibung elektromagnetischer Wellen Aus den Maxwellgleichungen folgt die Wellengleichung für den elektrischen (und den magnetischen) Feldvektor ∇ 2 E − μ 0ε 0 μ r ε r E μo εo μr εr ∂ E =0 2 ∂t 2 H elektrischer Feldvektor 4⋅10-7 Vs / (A m) Permeabilität des Vakuums 8.854⋅10-12 F / m Permittivität des Vakuums relative Permeabilität (ca. 1) relative Permittivität zwischen 1 und 80 (=Dielektrizitätskonstante) Pointing Vektor S=E×H Die Lichtgeschwindigkeit im Vakuum c ergibt sich mit: μo εo = 1/c2 Für die Lichtgeschwindigkeit im Medium cr ergibt sich mit: μo εo μr εr = 1/cr2 15 Strahlungsintensitätsmaße Poynting-Vector S variiert extrem schnell Strahlungsmessgeräte messen meist die Energie der Strahlung über ein bestimmtes Zeitintervall gemittelt (Leistung), die eingeschränkt auf einen Winkelbereich Ω auf eine beschränkte Fläche A fällt. Entsprechend gibt es folgende Maße: Strahlungsfluss radiant flux Φ Watt Strahlungsflussdichte radiant flux density F=dΦ/dA irradiance Strahldichte radiance I=d2Φ/dΩ dA cosΘ Watt m-2 sr-1 Strahlungsintensität radiant intensity L=dΦ/dΩ Watt m-2 Watt sr-1 Ist die Strahlung richtungsunabhängig (isotrop) gilt I = F/π. Oft werden diese Strahlungsgrössen spektral, d.h. für eine Wellenlänge λ oder eine Frequenz ν angegeben. 16 Wichtigste Größen: Nomenklatur Strahlungsflussdichte F [W/m²] gesamter Strahlungsenergiefluss durch eine Einheitsfläche Strahldichte I [W/(m²sr)] Strahlungsenergiefluss pro Einheitsfläche und Raumwinkel sr = Steradian, Raumwinkeleinheit (gesamter Winkelbereich=4π) Zusammenhang zwischen Strahlungsflussdichte und Strahldichte durch Integration über den Halbraum F= ∫π I (Ω) cos θ dΩ 2 I EF dΩ θ I ist der Energiefluss durch eine Einheitsfläche (EF) aus einer Raumwinkeleinheit, wobei aber die Einheitsfläche senkrecht auf dem Blickstrahl steht (daher cosθ in Integration für F. 17 Raumwinkelintegration dO = dU ϕ dU θ = (r sin θdϕ )(rdθ ) 14243 123 dU ϕ z dU θ 2 = r 2 sin θ d θ d ϕ = r dΩ 1424 3 dΩ dUθ O = ∫ dO = ∫ r 2 dΩ = r 2 ∫ dΩ ≡ 4πr 2 → ∫ dΩ = 4π dUφ θ φ y Raumwinkel werden in Steradian (sr) angegeben, so wie „normale“ Winkel in Radian (rad) angegeben werden. dθ , dϕ in rad ∈ [0 ,2π ] x dΩ in sr ∈ [0,4π ] 18 Isotrope Strahlung und Lambert-Reflektor Ein Körper strahlt isotrop (gleich in alle Richtungen), wenn er aus allen Richtungen gleich hell erscheint (z.B. Schnee). Ein Lambert-Reflektor reflektiert alle eintreffende Strahlung und verteilt sie isotrop. Bei isotroper Strahlung hängt also die Strahldichte I nicht vom Winkel ab: I (Ω) = I → F(isotrop ) = ∫ I (isotrop ) cos θdΩ 2π ∫π cosθdΩ = I (isotrop ) 2 1424 3 ∫ cosθ sin θdθdϕ = ∫ dϕ π∫ cosθ sin θdθ ≡( 2π )⋅( 12 ) =π 2π 2π 2 = I (isotrop )π 19 Strahlungsgesetze Planck'sches Strahlungsgesetz Bλ (T ) = Wien'sches Verschiebungsgesetz 2hc 2 λmax = λ5 1 ⎛ hc ⎞ ⎟⎟ − 1 exp⎜⎜ ⎝ k B λT ⎠ 2898 [ μm] T Stefan-Boltzmann Gesetz F(T) = πB(T) = σT 4 Kirchhoffsches Gesetz E (T ) = ε (λ ) 1λ23 Emission des grauen Körpers B (T ) 1λ23 Emission des schwarzen Körpers 20 Spektrale Einheiten Strahlung ist wellenlängenabhängig; daher lassen sich alle Strahlungsmaße auch spektral ausdrücken. Da wir die Spektralität durch verschiedene Maße (Wellenlänge, Frequenz, Wellenzahl) beschreiben können, gibt es auch verschiedene spektrale Strahlungsmaße, z.B. für die Strahlungsflussdichte F. ( ) [F ] = W / (m Hz ) = Ws / m [F ] = Wm / (m ) = W / m Fλ mit [Fλ ] = W / m 2 m = W / m 3 Fν mit Fk mit ν 2 2 2 k mit λ Wellenlänge, ν = c Frequenz, k = 2π Wellenzahl λ λ ∞ ν ( λ =∞ ) =0 k ( λ =∞ ) =0 0 ( =0 ) =∞ k k ( =0 ) =∞ F = ∫ Fλ dλ = Fν dν = ∫ F dk ∫ ν λ λ dF = Fλ dλ = − Fν dν = − Fk dk Fλ = dF dF dF , Fν = − , Fk = − dλ dν dk Damit gilt für Umrechnungen zwischen spektralen Einheiten: c ⎫ dν ⎛ c ⎞ Fλ = − Fν = − Fν ⎜ − 2 ⎟ = Fν 2 ⎪ λ ⎪ dλ 2π ⎝ λ ⎠ F F = ⎬ ν k c 2π ⎪ dk ⎛ 2π ⎞ Fλ = − Fk = − Fk ⎜ − 2 ⎟ = Fk 2 λ ⎪⎭ dλ ⎝ λ ⎠ Analoges gilt für spektrale Strahldichten Iλ, Iν, und Ik 21 Absorbiert ein Körper alle auf ihn auftreffende Strahlung (schwarzer Strahler), dann strahlt dieser Körper isotrop diese Energie wieder ab (Energieerhaltung) in einer eindeutigen Funktion der Temperatur T und der Wellenlänge λ, Bλ(T) (Planck, 1901) 3.0 Bλ(T) , 107 W/(m2sr μm) Planck'sches Strahlungsgesetz 3.5 6000 K 2.5 2.0 1.5 5000 K 1.0 4000 K 0.5 3000 K 0.0 0 Bλ (T ) = 2hc λ5 2 1 ⎛ hc ⎞ ⎟⎟ − 1 exp⎜⎜ ⎝ k B λT ⎠ 1 2 Wellenlänge, λ 3 4 k B = 1,38065 ⋅10 −23 J / K Boltzmann - Konstante, 22 Planck-Gesetz als f(ν) λ 5 1 ⎛ hc ⎞ ⎟⎟ − 1 exp⎜⎜ ⎝ k B λT ⎠ dB(λ) dλ = dB(ν) dν dλ = λ2 /c dν 3000 K 1E+006 W/(m2 sr μm Bλ (T ) = 2hc 2 6000 K 1E+007 ΣB , λ Im Mikrowellenbereich wird das Planck-Gesetz oft mit Frequenzen anstelle von Wellenlängen ausgedrückt: 1E+008 1E+005 1500 K 1E+004 750 K 1E+003 1E+002 300 K 1E+001 nahezu linear 1E+000 1E-001 1E-002 2 hν Bν (T ) = 2 c 3 1 ⎛ hν ⎞ ⎟⎟ − 1 exp⎜⎜ ⎝ k BT ⎠ 0.1 0 1 1.0 2 5 10.0 20 50 Wellenlänge λ, μm 23 100.0 Rayleigh- Jeans Näherung h ν << k T h c/λ << k T Näherung im Fall von bzw. gilt bei langen Wellenlängen und nicht zu tiefen Temperaturen gilt. ν= 30 GHz, T=300 K 2 hν 3 Bν (T ) = 2 c 2⋅10-21 1 ⎛ hν ⎞ ⎟⎟ − 1 exp⎜⎜ ⎝ k BT ⎠ << 4⋅10-21 2kν 2 2k B ≈ 2 ⋅T = 2 ⋅ T c λ Satelliten messen Strahldichte I [W m-2 Hz-1 sr-1] Mit I = ε B und der Annahme einer Emissivität ε=1 ergibt sich mit der Rayleigh-Jeans Näherung die äquivalente Schwarzkörpertemperatur TB (R-J) auch Helligkeitstemperatur genannt! Aber besser Planck-äquivalente TB TB ( R − J ) = λ2 2k B ⋅ Iν 24 Fernerkundung Infrarotkanal von METEOSAT - radiometrische Information: ⇒ Oberflächentemperaturen - räumliche Strukturinformation ⇒Wolkenarten, Küsten Meteorologische Satellitensensoren im Infraroten und Mikrowellenbereich messen Helligkeitstemperaturen. 25 Das Maximum der Planckschen Strahlung verschiebt sich mit zunehmender Temperatur nach kürzeren Wellenlängen ∂Bλ ∂λ ∂Bν ∂ν = 0 ⇒ λmax λmax 3.5 3.0 Bλ(T) , 107 W/(m2sr μm) Wien'sches Verschiebungsgesetz 2898 = [ μm] T 6000 K 2.5 2.0 1.5 5000 K 1.0 4000 K 0.5 3000 K 0.0 0 = 0 ⇒ ν max = 5,8789 ⋅10 T , Hz 10 λ 2 Wellenlänge, λ 3 4 ν max Achtung : ' max 1 = λ (ν max ) = c ν max 5099 c = = ≠ λmax 5,8789 ⋅1010 T T Beispiel: T=6000 K λmax=0,5 μm (grün) λ‘max=0,8 μm (nahes IR) 26 Bλ max (T ) = a λ 5 max log Bλ max (T ) = log a − 5 log λmax 3000 K 1E+006 W/(m2 sr μm Durch Einsetzen der Gleichung für λmax in die Planck-Funktion wird der Exponent unter dem Bruchstrich konstant und man erhält: 6000 K 1E+007 ΣB , λ Wien'sches Verschiebungsgesetz 1E+008 1E+005 1500 K 1E+004 750 K 1E+003 1E+002 300 K 1E+001 1E+000 1E-001 1E-002 0.1 0 1 1.0 2 5 10.0 20 50 100.0 Wellenlänge λ, μm D.h. die Planck-Funktion im Maximum Bλmax nimmt um genau 5 Größenordnungen ab, wenn die Wellenlänge λ um eine Größenordnung zunimmt. 27 Stefan-Boltzmann-Gesetz Das Stefan-Boltzmann-Gesetz gibt die Temperaturabhängigkeit der spektral integrierten Strahlungsflussdichte der Planck-Strahlung E an. E [Wm-2] lässt sich wie folgt aus der Planck-Strahlung ableiten: ∞ 2π ∞ 0 0 0 E (T ) = ∫ ∫ Bλ (T ) cos θ dΩdλ = π ∫ Bλ (T )dλ 2π k B4 T 4 π 4 4 = = σ T h 3c 2 15 E(T) = πB(T) = σT 4 σ = 5,67 ⋅10 −8Wm −2 K −4 Stefan - Boltzmann - Konstante 28 Kirchhoff'sches Gesetz Gesetz für den grauen Strahler: Absorbiert ein Körper nur den Teil ε(λ)<1 der auftreffenden Strahlung dann gilt für seine Ausstrahlung: Eλ (T ) = ε (λ ) 123 Emission des grauen Körpers Bλ (T ) 123 Emission des schwarzen Körpers Bλ(TB) Bλ(TB)(1-ε(λ))+ Bλ(TN)ε(λ) Bogenlampe (TB sehr heiss) „Selbstumkehr“ von Spektrallinien Natrium-Dampf absorbiert bei λN und emittiert –nur dort - entsprechend eigener Temperatur (TN viel kälter als TB) 29