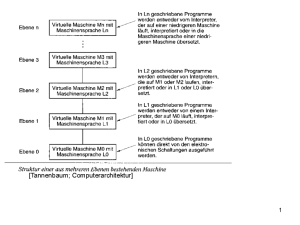
Das Rechnermodell

Das Rechnermodell - Funktion
• Darstellung von Zahlen und Zeichen im Rechner
– Darstellung von Zeichen
• ASCII-Kodierung
– Zahlensysteme
• Dezimalsystem, Dualsystem, Hexadezimalsystem
– Darstellung von Zahlen im Rechner
•
•
•
•
•
•
Natürliche Zahlen
Ganze Zahlen -- INTEGER
Darstellung mit Vorzeichenbit
Darstellung im Zweierkomplemet
Reelle Zahlen -- REAL
REAL-Zahlen nach Mikroprozessornorm erhöht genaue
Zahlendarstellung
• Genauigkeit der internen Zahlenrepräsentation
• BCD-Kodierung dezimaler Zahl
Das Rechnermodell - Funktion
• Darstellung von Zahlen/Zeichen im Rechner
– Bit (0/1) ist die kleinste Informationseinheit
– Größere Einheiten durch Zusammenfassen mehrerer Bits,
z.B. 8 Bit = 1 Byte, 4 Byte = 1 Wort
1 Byte =
8 Bit
0
1
Most Significant Bit
0
0
1
1
1
Least Significant Bit
– In einem Byte können 256 unterschiedliche Zustände
repräsentiert werden
000000  11111111
0
Das Rechnermodell - Funktion
• Darstellung von Zeichen im Rechner
– Zeichen werden durch eindeutige Byte-Codes kodiert
– Der ASCII-Zeichensatz ist der "Urvater" aller Zeichensätze
• Er enthält 27 = 128 Zeichen
• Die lateinischen Grundbuchstaben, Zahlen und einige spezielle
Zeichen
• Er ist sozusagen der kleinste gemeinsame Nenner aller
anderen Zeichensätze
• Der erweiterte ASCII Zeichensatze enthält 28 = 256 Zeichen
– In der ersten Hälfte identisch mit dem 7 Bit ASCII Zeichensatz
– In der zweiten Hälfte enthält er je nach Sprache und
Computersystem verschiedene weitere Zeichen, z.B. Umlaute
Das Rechnermodell - Funktion
• 7 Bit ASCII Interchange-Kodierung von Zeichen
American
Standard
Code of
Information
Interchange
Das Rechnermodell - Funktion
• Erweiterung des 7-Bit ASCII-Codes
– Verfügbares MSB-Bit als Paritätsbit zur Erkennung von
Übertragungsfehlern
• Setze MSB-Bit so, daß Summe aller Bits gerade/ungerade
• Wenn nicht erfüllt, dann Übertragungsfehler
– Verfügbares MSB-Bit zur Erweiterung des Zeichensatzes
• z.B. länderspezifische Erweiterungen - ä ö ü ß etc.
Das Rechnermodell - Funktion
• Ein/Ausgabemedien müssen entsprechende
Zeichen-Codes senden/empfangen und darstellen
– z.B. Tastaturtreiber müssen ASCII Zeichen-Codes
generieren
– Das Aussehen der Zeichen wird durch die Schriftart oder
den Font festgelegt
• Können beliebig gewählt werden
• Geben vor, wie ein Zeichen auf dem Ausgabemedium erscheint
Byte-Wert (interne Repräsentation) 252
Zeichensatz, z.B. ASCII, 252 = ü
Schriftart (Font), realisiert
Zeichen
Das Rechnermodell - Funktion
• Repräsentation und Bearbeitung von Zahlen
– Zahlensysteme:
•
•
•
•
•
•
Repräsentation einer Zahl Z in einer Zahlenbasis
Z = i XiYi , (i  , 0  X  Y)
Y: Basis des Zahlensystems
X: Ziffernvorrat
Negative Exponenten beschreiben Nachkommastellen
Bsp.: Dezimalsystem: Y =10, 0  X  10
– Z = 3240.4 = 3·103 + 2·102 + 4·101 + 0·100 + 4·10-1
– Prinzipiell kann die Basis beliebig gewählt werden
• Gängige Basen sind Y = 2 (Binär), Y = 10 (Dezimal),
Y = 16 (Hexadezimal)
Das Rechnermodell - Funktion
• Dual- oder Binärzahlen
– Basis Y=2, Ziffernvorrat = 0,1 (repräsentiert durch 1 Bit)
– Bsp.: 01101100 =
0·27+1·26+1·25+0·24+1·23+1·22+0·21+0·20
• Hexadezimalsystem
– Basis Y=16, Ziffernvorrat 0-9, A-F
– Bsp.: 6A = 6·161 + 10·160 = 106
• Zur Umrechnung von Dualdarstellung in
Hexadezimaldarstellung splittet man 1 Byte in 2
Halbbytes
– 106 = 0110 1010 = 6A
Das Rechnermodell - Funktion
• Umrechnung von Dezimalzahlen in Dualzahlen
– Restwertmethode
37
18
9
4
2
1
:
:
:
:
:
:
2
2
2
2
2
2
=
=
=
=
=
=
18
9
4
2
1
0
Rest
Rest
Rest
Rest
Rest
Rest
1 +------> 100101
0
1
0
0
1
Das Rechnermodell - Funktion
• Umrechnung von gebrochenen Zahlen durch Zerlegung in den
ganzzahligen und gebrochenen Teil (Bsp: 37.2)
– Umrechnung des ganzzahligen Teils der Dezimalzahl
– Umrechnung des gebrochenen Anteils der Dezimalzahl mittels
fortgesetzter Multiplikation
0,2 · 2 = 0,4
0,4 · 2 = 0,8
0,8 · 2 = 1,6
_________|
|
0,6 · 2 = 1,2
_________|
|
0,2 · 2 = 0,4
--> 0
--> 0
--> 1
--> 1
--> 0
37.2 =
100101.00110
+------> 00110...
Das Rechnermodell - Funktion
• Beispiel Zahlenkonvertierung
dezimal binär hex
0
1
2
3
4
5
6
7
0000
0001
0010
0011
0100
0101
0110
0111
0
1
2
3
4
5
6
7
dezimal binär hex
8
9
10
11
12
13
14
15
1000
1001
1010
1011
1100
1101
1110
1111
8
9
A
B
C
D
E
F
Das Rechnermodell - Funktion
• Zahlendarstellung im Rechner
– Natürliche Zahlen (positive ganze Zahlen)
– Anzahl von darstellbaren Zahlen hängt ab von der Anzahl
von Bytes, die zur Repräsentation zur Verfügung stehen
– 1 Byte: Wertebereich von 0-255
• Entspricht in einigen Programmiersprachen dem Typ byte
– 2 Byte: Wertebereich von 0-65535
• Entspricht in einigen Programmiersprachen dem Typ short
– 4 Byte: Wertebereich von 0-(232 -1)
• Entspricht in einigen Programmiersprachen dem Typ int
Das Rechnermodell - Funktion
• Zahlendarstellung im Rechner
– Ganze Zahlen (Integer-Zahlen)
• Signed oder vorzeichenbehaftet
– Alternative 1: Reservierung eines Bits für das Vorzeichen
und Kodierung wie gehabt
• Zahlenbereich bei 8 Bit: -127 bis +127
• Es gibt +0 und -0
– Alternative 2: Darstellung negativer Zahlen im Zweierkomplement ( X=Bn+1-X )
• Negation aller Bits der positiven Zahl und anschließende
Addition von 1
• 106 = 0110 1010, -106 = 10010101+00000001 = 10010110
• Zahlenbereich bei n Bits: -2n bis 2n-1
Das Rechnermodell - Funktion
• Zahlendarstellung im Rechner
– Reele Zahlen (Gleitkomma-Darstellung)
– Genauigkeit der internen Repräsentation hängt ab von der
Anzahl von Bytes, die zur Repräsentation zur Verfügung
stehen
– 4 Byte:
• Entspricht in einigen Programmiersprachen dem Typ float
– 8 Byte:
• Entspricht in einigen Programmiersprachen dem Typ double
Das Rechnermodell - Funktion
• Zahlendarstellung im Rechner
– IEEE-Norm (Institute of Electrical and Electronics Engineers)
– Gleitkommazahl p (4 Bytes) wird dargestellt als
•
•
•
•
•
Bits
p = (-1)s · |m| · Be
s = sign(m): Vorzeichenbit
m: Mantisse
B: Basis
e: exponent
31 30
-
23 22
-
s
exp
m
1Bit
8Bit
23Bit
Vorzeichen exp = e+127
Mantisse
0
Das Rechnermodell - Funktion
• Gleitkommadarstellung
– In der Mantisse werden Werte von 0.0 bis 0.11...1 (Dual)
repräsentiert
• Bsp.: 0.12 = 1/2 = 0.5; 0.012 = 1/4 = 0.25
• Kleinste Zahl ist: 0.00..012 (1 in Position 2-23)
• Da das höchstwertige Bit immer 0 ist, wird es nicht kodiert
(Hidden-Bit)
Das Rechnermodell - Funktion
• Gleitkommadarstellung
– Den Wert des Exponenten erhält man durch Subtraktion
von 127 (Hälfte des Wertebereichs) von dem in den 8 Bit
dargestellten ganzzahligen Wert
• Werte von –127 bis 128 sind somit möglich
• -127 und 128 jedoch für Spezialfälle reserviert
• -127: 0, 128 (m=0): Infinity, 128(m0): NaN: ungültiger Wert
Das Rechnermodell - Funktion
• Gleitkommadarstellung
– Bei 8 Byte Darstellung:
•
•
•
•
s: 1 Bit
m: 52 Bit
e: 11 Bit
Höhere Genauigkeit, da Wertebereich
32-Bit-Genauigkeit: -3.402824·1038 bis 3.402824·1038
64-Bit-Genauigkeit: -1.797693·10 308 bis 1.797693·10308
Das Rechnermodell - Funktion
• Bsp.: Normalisieren einer 64-Bit-genauen
Gleitkommazahl p=(0.0001101002)·21
–
–
–
–
Interne Darstellung:
s=0; exp=(e=1)+1023; m=000110100...0
p: 0 10000000000 000110100...0
Normalisierung:
•
•
•
•
Verringern des Exponenten um 3 und gleichzeitiges ...
... Verschieben der Mantisse um 3 Stellen nach links
Ergebnis: 0 01111111101 110100...0
p=+(1·2-1 + 1·2-2 + 0·2-3 + 1·2-4) · 21021-1023=0.203125
Das Rechnermodell - Funktion
• Integer-Arithmetik
– Addition (mit 4 Bit Darstellung):
3
0011
+ 2 + 0010
--- -----5
0101
7
+9
--16
0111
+ 1001
-----(1)0000
Overflow
– Subtraktion durch Addition negativer Zahlen (Y-X=Y+X)
•
•
•
•
Y-X = Y–(X–2n+1+2n+1) = Y+2n+1–X–2n+1 = Y+X–2n+1
Negative Zahl wird hier im 2er-Komplement dargestellt
2er-Komplement: Bitweises negieren und addieren von 1
-0110 = (1001+1) = 1010
Das Rechnermodell - Funktion
• Integer-Arithmetik
12
01100
-5 -00101=11010+1=11011
-------------7 100111
– Übertrag nur dann Overflow, wenn Vorzeichen beider
Zahlen gleich und das Ergebnis ein anderes Vorzeichen hat
– Bsp: +(-12)+(-12) = 10100 +10100 =101000
Das Rechnermodell - Funktion
• Integer-Arithmetik
– Algorithmus zur Multiplikation
• Nach denselben Regeln, nach denen Dezimalzahlen
multipliziert werden
• Stellenweises multiplizieren des Multiplikanten mit dem
Multiplikator und addieren der Teilergebnisse
– Bsp.:
10111 * 01100
00000
00000
10111
10111
00000
100010100
Das Rechnermodell - Funktion
• Integer-Arithmetik
– Optimierung der Multiplikation durch Bitverschiebung
• Verschieben um 1 Position nach rechts = Division durch 2
• Verschieben um 1 Position nach links = Multiplikation mit 2
– Algorithmus (X*Y):
1)
2)
3)
4)
5)
Ergebnis = 0
wenn letztes Bit von Y = 1, dann addiere X zum Ergebnis
Verschiebe Y um eine Stelle nach rechts
Verschiebe X um eine Stelle nach links
wenn Y ungleich 0, dann wiederhole beginnend mit Schritt 2
Das Rechnermodell - Funktion
• Integer-Arithmetik
– Multiplikation durch Bitverschiebung
– Bsp.: 1001 x 1101
Wiederholung
1
2
3
4
Shift rechts
1101
110
11
1
Shift links
1001
10010
100100
1001000
1001 + 00000 + 100100 + 1001000
Ergebnis: 1110101
Das Rechnermodell - Funktion
• Integer-Arithmetik
– Division – mittels Addition, Subtraktion und Bitverschiebung
– Algorithmus (X/Y):
1)
2)
3)
4)
5)
6)
Quotient Q = 0, Rest = X, T = Y
Verschiebe T bis T>Rest (wie oft geht Y in X)
Wenn T = Y: Ende
Verdopple Q (<<1) und halbiere T (>>1)
Wenn T<=Rest: Rest=Rest-T und Q = Q+1
Wiederhole beginnend mit Schritt 3
Das Rechnermodell - Funktion
• Integer-Arithmetik
5
00101
-12 -01100=10100
--------------7 11001
Betrag von 11001=
(durch Bildung des 2er-Komplement) 00111
Das Rechnermodell - Funktion
• Gleitkomma-Arithmetik
– Addition/Subtraktion:
• Exponenten angleichen (Verschieben der Mantisse des
Operanden mit kleineren Exponenten
• Mantissen addieren/subtrahieren
• Ergebnis normalisieren
• Beispiel: 12 + 20 =
(110 · 24)+(101 · 25)=
(0110 · 25)+(1010 · 25)=
1,0000·25=1·26
Das Rechnermodell - Funktion
• Gleitkomma-Arithmetik
– Multiplikation/Division:
•
•
•
•
Multiplikation/Division der Mantissen
Exponenten addieren/subtrahieren
Ergebnis normalisieren
Beispiel: 12 · 20 =
(110·24)·(101·25)=
110·101·29=011110·29=11110·28=240