Kepler-Gesetze im Kontext

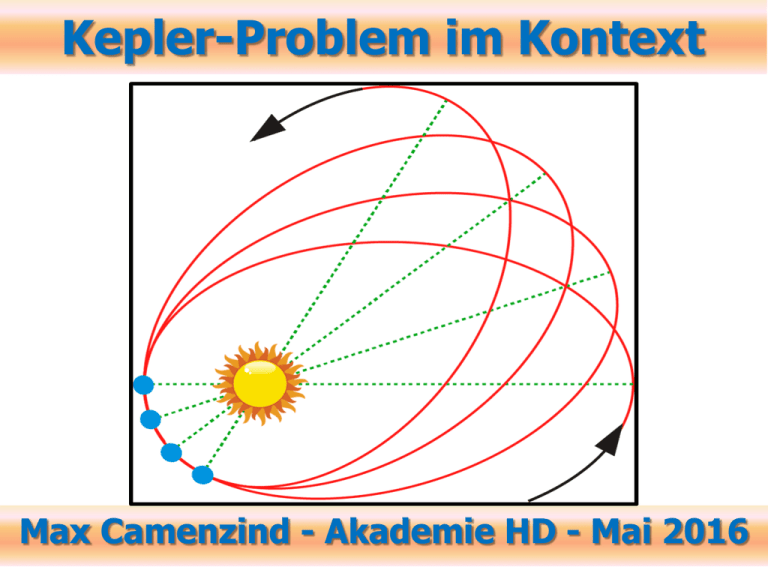
Kepler-Problem im Kontext
Max Camenzind - Akademie HD - Mai 2016
Zusammenfassung aus Herleitung
2-Körper-Problem
Ellipsengleichung mit Mittelpunkt in (0,0):
Eine Ellipse ist durch 2 Parameter bestimmt!
Eine Ellipse ist die Menge aller Punkte mit
y
x
Zusammenfassung
2-Körper-Problem
Bewegung eines Planeten, Asteroiden oder Kometen wird
durch 2 zeitlich erhaltene Parameter bestimmt:
 1. durch totale Energie E = T + V = const
E < 0  gebundene Systeme
 2. durch Drehimpuls J = mr² dq/dt = const
Polarform einer Ellipse ist durch 2 Parameter bestimmt:
 Semilatus Rectum p
 Exzentrizität e; e = 0  Kreisbahn.
GmMm
 C  1/ p
2
J
2
2 EJ
e  1
2
m(GmM )
Polarform: r(f) = p/(1 + e cos(f))
p
p = a(1 – e²)
2-Körper-Problem 
3 Mögliche Bahnformen
Bewegung eines Planeten, Asteroiden oder Kometen wird
durch 2 zeitlich erhaltene Parameter bestimmt:
 1. durch totale Energie E = T + V = const
E < 0  gebundene Systeme
 2. durch Drehimpuls J = mr² dq/dt = const
Es sind 3 Fälle möglich:
 1. E < 0: e < 1: gebundene Bahn: Ellipse oder Kreis
Satelliten, Planeten, Kometen, DSterne
 2. E = 0: e = 1: Parabelbahn: z.B. Kometen aus
der Oortschen Wolke
 3. E > 0: e > 1: Hyperbelbahn: Streubahn, z.B.
ein Weißer Zwerg aus der Milchstraße
3 BahnTypen:
Kreis +
Ellipse
Parabel
Hyperbel
F: Fokalpunkt
Kepler-Gesetze im Kontext
Tycho Brahe/
Tyge Ottesen
Brahe de Knudstrup
(1546-1601)
Johannes Kepler
(1571-1630)
• Kepler 1: “Die Planeten bewegen sich auf
elliptischen Bahnen mit der Sonne in einem Fokus.”
 m(GmM ) / 2 J  E  0
2
2
0  e 1
Kepler-Gesetze im Kontext
• Kepler 2: “Der Radius-Vektor zu einem Planeten
überstreicht in gleichen Zeiten gleiche Flächen”
dA  dq 
 r r  / 2
dt
 dt 
2 
A  r q  J  const
2
2m
dA  r (rdq ) / 2
• Kepler 3: “Das Quadrat der Umlaufperioden skaliert
mit der 3. Potenz der Halbachsen”
4 ma
P 
k
2
2
3
ma 3
a3
P  2
 2
k
G ( m1  m 2 )
Flächensatz  Bahnperiode P
Das 3. Kepler-Gesetz folgt durch Integration
aus dem Flächensatz: Fläche(Ellipse) = ab
k = GmM
3. Kepler-Gesetz Sonnensystem
Gesamtenergie  Halbachse a
Geschwindigkeit der Planeten
folgt aus dem Energiesatz
Beispiel: Komet Halley
Perihel: 0,586 AE; Aphel: 35,082 AE
r = a(1 – e) = 0,586 AE;
ra = a(1 + e) = 35,082 AE.







a = (r + ra)/2 = 17,834 AE
e = 1 – r/a = 0,967
v² = (GMS/a)(2a/r – 1) = 49,95x106x59,86
v = 54,57 km/s
v²a = (GMS/a)(2a/ra – 1) = 49,95x106x0,017
va = 0,913 km/s
3. Kepler: P = 75,32 a (siderisch)
Bahn des Kometen Halley
 Lang gestreckte Ellipse: P = 76 Jahre
langsam
schnell
Komet Halley
Anomalien im Kepler-Problem
Kreis
Orbit
Grafik: Wikipedia
M: mittlere Anomalie
E: exzentrische
Anomalie
q: wahre Anomalie
Anomalien im Kepler-Problem
Exzentrische E und wahre Anomalie q
Mittlere
Anomalie:
M=nt
Orbit-Berechnung mit Kepler-Glg.
Gegeben ein Zeitpunkt t (als Julianisches Datum).
 mittlere Anomalie M = n(t – t0); t0: Periheldurchgang.
Aus Lösung der Kepler-Gleichung folgt E  (x,y).
Aus E folgt die wahre Anomalie q.
Damit ist der Bahnpunkt (r,q) bestimmt.
Umrechnen auf ekliptikale Koordinaten.
Translation auf geozentrisch ekliptikale Koordinaten.
Umrechnen auf geozentrisch äquatoriale Koordinaten.
Am Teleskop einstellen, auch in Stellarium benutzt.
2-Körper Orbit am Himmel
Schwerpunkt läuft linear über Himmel
Was Kepler nicht wusste 
Apsidendrehung der Ellipse
Apsidendrehung der Ellipse
Die Apsidendrehung einer elliptischen
Umlaufbahn ist eine fortschreitende Drehung der
ganzen Bahn in der Bahnebene. Dabei dreht sich
die Apsidenlinie kontinuierlich, während Form
und Ebene der Bahn im Raum gleich bleiben. Je
nach Zentralkörper werden auch folgende
Bezeichnungen verwendet:
 Periheldrehung, oder auch Präzession des
Perihels, wenn die Bahn die Sonne umläuft und
 Perigäumsdrehung, wenn die Bahn die Erde
umläuft, also das Perigäum betrachtet wird.
 Periastrondrehung, wenn es sich um Bahnen
in Doppelsternsystemen handelt.
Ursache der Apsidendrehung
Eine Apsidendrehung entsteht, wenn ein
Himmelskörper auf seiner elliptischen Umlaufbahn
um einen Zentralkörper bestimmten äußeren
Störungen unterliegt. Wäre der Himmelskörper
einer Anziehungskraft ausgesetzt, welche streng
umgekehrt quadratisch mit der Entfernung vom
Zentralkörper abnimmt, so würde er sich exakt auf
einer Keplerellipse bewegen, deren Form, Lage und
Orientierung im Raum unverändert blieben.
Abweichungen vom streng umgekehrtquadratischen Kraftgesetz führen jedoch zu
verschiedenen Arten von Bahnstörungen, welche
Form, Lage und Orientierung der Bahn verändern
können. Eine dieser Bahnstörungen ist die
Apsidendrehung.
Eine mögliche Ursache für Abweichungen
vom idealen Kraftgesetz ist die Gegenwart
anderer Körper, welche zusätzliche
Gravitationskräfte auf den betrachteten
Himmelskörper ausüben. Im Falle der
Planetenbahnen ist der Einfluss der jeweils
anderen Planeten die Hauptursache für die
Periheldrehungen.
Zusätzlich unterliegen alle Planeten und
Asteroiden einer relativistischen Apsidendrehung, verursacht durch die Metrik der
RaumZeit. Sie wurde zum ersten Mal von
Albert Einstein 1915 für Merkur berechnet.
Eine andere Ursache kann in Abweichungen des Zentralkörpers
von der Kugelform liegen. Während ein exakt kugelsymmetrisch
aufgebauter ausgedehnter Körper dasselbe streng inversquadratische Gravitationsfeld erzeugen würde wie ein punktförmiger Körper derselben Masse, führen unregelmäßige Masseverteilungen oder der Äquatorwulst abgeplatteter Zentralkörper
wiederum zu Abweichungen vom invers-quadratischen Kraftgesetz
und damit zu Bahnstörungen. Der Äquatorwulst der Erde verursacht (neben anderen Bahnstörungen) Perigäumsdrehungen bei
künstlichen Erdsatelliten. Die Abplattung der Sonne verursacht
Periheldrehungen der Planetenbahnen, welche wegen der
Geringfügigkeit der Abplattung und des großen Abstandes der
Planeten jedoch wesentlich kleiner sind als die von den Planeten
untereinander verursachten Drehungen.
 Schließlich kann das physikalisch reale Kraftgesetz auch grundsätzlich vom idealisierten invers-quadratischen Verhalten abweichen. Gemäß der Allgemeinen Relativitätstheorie ist dies für die
Gravitationsfelder, denen die Planeten ausgesetzt sind, tatsächlich
der Fall (wenn auch nur in sehr geringem Ausmaß), so dass ein
weiterer Beitrag zu den Periheldrehungen der Planeten entsteht.
Planeten Apsidendrehung
Planet
Merkur
Tropisch
[° / Jh.]
1,556
Siderisch
[° / Jh.][´´/Jh.]
0,159 = 572´´
Venus
Erde
Mars
Jupiter
Saturn
Uranus
Neptun
1,402
1,720
1,841
1,613
1,964
1,486
1,426
0,005
0,323
0,444
0,216
0,567
0,089
0,029
Apsidendrehung Merkurbahn
Periode: 88 Tage
Apsidendrehung:
 1850:
Urbain Le Verrier
530`` /Jahrhundert
571,9``/Jahrhund.
280`` auf Venus
150`` auf Jupiter
100`` andere Plan.
------------------------43,11``/Jahrhund.
als Diskrepanz
Le Verrier, der durch die Untersuchung unerklärter Anteile
in den Bahnstörungen des Uranus bereits erfolgreich die
Entdeckung Neptuns ermöglicht hatte, vermutete als
Ursache der Diskrepanz bei Merkur eine Störung durch
einen bislang unbekannten Planeten auf einer Bahn
innerhalb der Merkurbahn. Dieser Planet erhielt den
Namen Vulkan, konnte jedoch trotz ausgedehnter Suche –
unter anderem während mehrerer Sonnenfinsternisse –
nicht entdeckt werden. Ebenso konnte auch kein für die
Störungen verantwortlicher sonnennaher
Asteroidengürtel nachgewiesen werden. Andere
verdächtigten den für das Zodiakallicht verantwortlichen
Staubgürtel oder sahen zumindest einen Teil der Ursache
in einer wegen ihrer Rotation abgeplatteten Gestalt der
Sonne (siehe auch unten), blieben mit ihren
Erklärungsversuchen aber letztlich ebenfalls erfolglos.
Gravitationsfeld Sonnensystem
Gravitationsfeld im Sonnensystem hat in metrischen Theorien
folgende Gestalt:  sog. Robertson Parameter ß und g
Einstein: g  1  b ; Lorentz-Invarianz: h  4b  g  3  0
Nicht-Linear
Krümmung
Sonnenquadrupol
= 2,18 x 10-7
pN-Geometrie Sonnensystem
& Periheldrehung / g = 1 = b
PPN Parameter:
Was messen g und b ?
Der ppN Parameter g misst den Überschuss an
räumlicher Krümmung, der durch eine
Einheitsmasse erzeugt wird.
Der ppN Parameter b misst die Nicht-Linearität
in der Superposition der Gravitationsfelder.
In der Einstein Theorie gilt:
In einer Gravitationstheorie mit
Skalarfeld (Brans-Dicke) treten
Abweichungen auf.
gE = 1 = bE
Warum ist g interessant ?
Welche Masse erzeugt Krümmung?
Im heutigen Universum erwartet man eine
Abweichung von der Größenordnung
Ein langreichweitiges Skalarfeld würde die
Einstein Theorie zu Fall bringen, ebenso das
Äquivalenzprinzip (Verletzung der Universalität
der physikalischen Konstanten!).
Die genaue Abweichung hängt von der konkreten
Theorie ab.
Alle Planeten unterliegen
Relativistischer Periheldrehung
Planet
Theorie
Beobachtung
Merkur
42,98`` / Jh.
43,11 +- 0,45`` / Jh.
Venus
8,6`` / Jh.
8,4 +- 4,8`` / Jh.
Erde
3,8`` / Jh.
5,0`` +- 1,2`` / Jh.
Mars
1,4`` / Jh.
1,5`` +- 0,15`` / Jh.
Icarus
10,3`` / Jh.
9,8`` +- 0,8`` / Jh.
Relativistische Periastrondrehung
ist in Pulsar-Systemen stark
a = Sonnenradius  einige Grad pro Jahr
PSR1913+16: a = 1,95 Mio. km, e = 0,617, M1 = 1,441, M2 = 1,387 MS
Ellipsen schrumpfen durch
Graviationswellenabstrahlung
 Merging von
Schwarzen Löchern &
Neutronensternen in 100 Mio. a
Fazit
• Die Newton`sche Theorie der Gravitation
konnte erfolgreich die drei Kepler-Gesetze
ableiten.  Es gibt jedoch 3 Bahnformen.
• Zusätzlich kann sie die beiden Konstanten im
2. und 3. Kepler-Gesetz durch physikalische
Größen erklären!
• In der Einstein`schen Theorie der Gravitation
sind die Kepler-Gesetze jedoch nur noch
Näherungen im Newton`schen Limes.
• Hier treten Apsidendrehung und Schrumpfen
durch Gravitationswellenabstrahlung auf.