Ubungsblatt 6 - Astrophysik Uni

Grundkurs Astrophysik I, WS 2012/13
W.-R. Hamann
Übungsblatt 6
(Ausgabe 20.12.2012, Abgabe 15.01.2013)
1. Aufgabe Der Halleysche Komet (5 Punkte)
Der Komet Halley hatte am 9. Februar 1986 seinen letzten Periheldurchgang bei
einer Periheldistanz von rp “ 0.5871 AU. Die numerische Bahnexzentrizität beträgt
“ 0.9673
(a) Wie groß sind dann die große und die kleine Bahnhalbachse? (2 Punkte)
(b) Wann erfolgt der nächste Periheldurchgang? (1 Punkt)
(c) Ermitteln Sie seine Bahngeschwindigkeit vprq in Abhängigkeit vom Sonnenabstand r. Wie groß ist insbesondere v im Perihel und Aphel? (2 Punkte)
Hinweis: Die Gesamtenergie auf einer Ellipsenbahn ist Eges “ ´GmM {p2aq.
2. Aufgabe Roche-Volumen (4 Punkte)
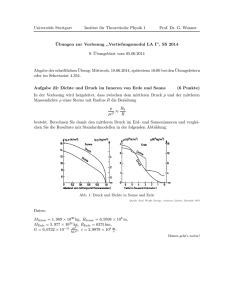
Im Rahmen des reduzierten Dreikörperproblems ist es sehr nützlich, den Einflussbereich der Schwerkraft um die jeweiligen Körper m1 , m2 abzuschätzen. Dieser ist
durch den Punkt L1 , der sich zwischen m1 und m2 befindet, als sogenannte HillSphäre mit Radius mi L1 gegeben. Die Hill-Sphäre liefert eine Näherung für das
Roche-Volumen um mi (auf dessen Oberfläche das Roche-Potenzial den Wert ΦpL1 q
annimmt): Körper innerhalb des Roche-Volumens werden zu mi gezogen.
alpha
m1
a
m2
L1
Hillsphere
Abbildung 1: Hill-Sphäre
(a) Bezeichnet a den Abstand zwischen m1 und m2 , so ist der Radius α der HillSphäre von m2 (in niedrigster Ordnung) gegeben durch:
c
1 m2
α«a3
(1)
3 m1
Befindet sich der Erdenmond innerhalb der Hill-Sphäre der Erde im System
Sonne-Erde? Was bedeutet das Ergebnis? (1 Punkt)
(b) β Lyrae AB ist ein Doppelsternsystem mit einer Umlaufdauer von 12.94 d.
Stern A hat einen Radius von 19 Rd bei einer Masse von ca. 2 Md und Stern
B einen Radius von 15 Rd bei einer Masse von 12 Md . Man weiß, dass es
W.-R. Hamann
Grundkurs Astrophysik I, WS 2012/13
zwischen beiden Sternen einen Massenaustausch gibt. Ein Stern kann dann
Material an seinen Partner abgeben, wenn er sein Roche-Volumen (« HillSphäre) ausfüllt. Ermitteln Sie mithilfe der genannten Daten und Gl. (1), in
welche Richtung(en) der Massenaustausch stattfindet. (3 Punkte)
3. Aufgabe Roche-Grenze (4 Punkte)
In der Vorlesung haben Sie von der differentiellen Wirkung der Gravitationskraft
(Gezeitenkräfte) auf einen ausgedehnten Körper gehört. Untersuchen Sie, unter welchen Bedingungen der Körper ( Satellit“) durch Eigengravitation zusammenhalten
”
kann.
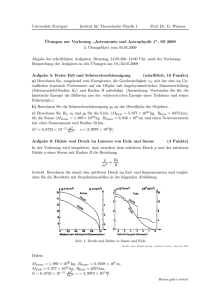
Denkt man sich dazu den Satelliten aus zwei gleichen Körpern der Massen m und
Radien r im Abstand d von einem Körper der Masse M mit Radius R, so gibt es
einen Abstand dR (Roche-Grenze), unterhalb dessen die Gezeitenkraft infolge der
Masse M stärker ist als die gravitative Anziehung der Massen m untereinander und
der Satellit somit zerbrechen würde.
m1
m2
M
R
r1
d-r
r2
d
d+r
Abbildung 2: Roche-Grenze
(a) Zeigen Sie, dass dann - unter Vernachlässigung von Rotation - die RocheGrenze gegeben ist durch
c
M
3
dR “ 16r3
(2)
m
Berücksichtigen Sie wegen r ! d bei der Herleitung nur Terme 1. Ordnung in
pr{dq. (2 Punkte)
(b) Berechnen Sie dR in Einheiten von RF für einen Saturnmond mit % “
1.1 g cm´3 . Die Dichte des Saturns beträgt %F “ 0.7 g cm´3 , benutzen Sie diese
Daten zur Lösung, modifizieren Sie ggf. Gl. (2).
Vergleichen Sie diesen Wert mit der Beobachtung, dass die Saturnringe zwischen 1.2 und 2.3 RF liegen, und interpretieren Sie. (2 Punkte)
Grundkurs Astrophysik I, WS 2012/13
W.-R. Hamann
4. Aufgabe Helligkeiten (2 Punkte)
(a) Die Gesamthelligkeit eines Dreifach-Sternsystems beträgt 0.0 mag. Zwei der
gebundenen Sterne haben Helligkeiten von 1.0 mag bzw. 2.0 mag. Wie groß ist
die Helligkeit des dritten Objekts?
(b) Ein Stern mit einer absoluten Helligkeit von MV “ 5 mag explodiert in der
Andromeda-Galaxie (Entfernung 690 kpc) als Supernova und wird milliardenfach heller. Wie groß wird die scheinbare V-Helligkeit? Wird die Supernova
heller als Wega?
5. Aufgabe Schwarzkörperstrahlung (5 Punkte)
(a) Bestimmen Sie die Anzahl N der Photonen pro Einheitsvolumen (Anzahldichte) in einem Schwarzkörperstrahlungsfeld der Temperatur T . Integrieren Sie
Bν geteilt durch die Energie eines einzelnen
dazu die Energiedichte uν “ 4π
c
Photons. (3 Punkte)
Hinweis: Es gilt:
ż 8 k´1
x
dx “ Γpkqζpkq mit k ą 1
(3)
x
0 e ´1
ř
1
mit der Riemannschen Zetafunktion ζpkq “ 8
n“1 nk und der Gammafunktion
Γpkq mit Γpkq “ pk ´ 1q! für k P N. Für die Zetafunktion gibt es die bekannten
Werte für positive, ganzzahlige Argumente:
ζp2q “
π2
6
ζp4q “
π4
90
ζp6q “
π6
945
(4)
Für ganzzahlige, ungerade Werte sind keine geschlossenen Darstellungen bekannt. Fur ζp3q gilt die von M. Lerch im Jahre 1900 gefundene, laut Wikipedia
besonders elegante“, Darstellung:
”
8
ÿ
1
7π 3
ζp3q “
´2
« 1.2021
(5)
3
2πn
180
n pe ´ 1q
n“1
Weitere Werte lauten:
ζp5q “ 1.0369
ζp7q « 1.0083
(6)
(b) Wie groß ist die mittlere Photonenenergie (Energiedichte geteilt durch die
Anzahldichte)? Welche mittlere Energie ist größer, die der Photonen oder die
kinetische Energie der Gasteilchen (einatomiges Gas) derselben Temperatur?
(2 Punkte)
6. Aufgabe Formales Integral (2 Punkte)
Berechnen Sie für eine planparallele Atmosphäre mit konstanter Quellfunktion S “
1{2 und der optischen Dicke τmax die emergente Intensität I ` pτ “ 0, µq. Dabei sei
die Einstrahlung am inneren Rand durch I ` pτmax , µq “ 1 (für alle µ ą 0) gegeben.
W.-R. Hamann
Grundkurs Astrophysik I, WS 2012/13
7. Zusatzaufgabe Planeten: Science vs. Fiction (4 Punkte)
Während erst seit den 90er Jahren wissenschaftlich erwiesen ist, dass andere Sterne
auch über Planeten verfügen, wird dies seit Jahrzehnten in Sciene-Fiction-Werken
vorausgesetz, dafür nimmt man es dort oft mit der Physik nicht so genau. Besonders viele Details zu einigen seiner Planeten (u.a. Durchmesser, Schwerebeschleunigung, Achsneigung, Anzahl der Monde, ...) gibt Blizzard Entertainment auf seiner
Webseite zum Computerspiel StarCraft II an. Berechnen Sie analog zum letzten
Übungsblatt die mittleren Dichte der folgenden Planeten unter der Annahme einer
perfekten Kugelgestalt:
Durchmesser in km
Planet
Aiur
12273
Braxis
9480
Char
10521
Korhal
12248
Mar Sara
9265
Moria
13528
New Folsom
6391
Shiloh
10694
Tarsonis
8894
Umoja
9543
g in cm/s2
961.38
804.42
892.71
961.38
1069.29
1137.96
1275.30
961.38
941.76
902.52
M in MC
hρi in g/cm3
Sind die Ergebnisse realistisch? Vergleichen Sie auch die Resultate mit den Werten
bekannter Objekte im Sonnensystem. (s. dazu Übungsblatt 5)