Signalverarbeitung 2 Signalverarbeitung 2

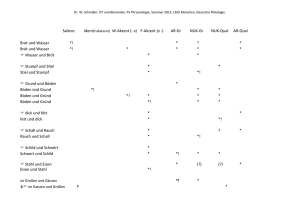
Signalverarbeitung 2
Volker Stahl
Signalverarbeitung 2
Volker Stahl
-1-
Überblick
Bessere Modelle, die nicht nur den Mittelwert von Referenzvektoren
sondern auch deren Varianz berücksichtigen
Weniger Fehlklassifikationen
Mahalanobis Abstand
Besseres Abstandsmaß basierend auf Normalverteilungsannahme
Zufallsvariablen, Dichtefunktion
Zufallsvektoren, gemeinsame Dichte
Anwendung im Viterbi Training
Signalverarbeitung 2
Volker Stahl
-2-
Einfachster Spezialfall
Vektorfolgen Länge 1
Vektordimension 1
Abstand von einfachen Zahlen
Beispiel
Referenzmuster
Klasse A:
Referenzmuster
Klasse B:
Zu klassifizierendes
Testmuster:
Abstandsmaß: Absoluter (quadrierter) Abstand zum Klassenmittelwert
Signalverarbeitung 2
Volker Stahl
-3-
Beispiel: Mehrere Referenzmuster pro Klasse
Referenzmuster
Klasse A:
Referenzmuster
Klasse B:
Zu klassifizierende
Testmuster:
Signalverarbeitung 2
Volker Stahl
-4-
Beispiel: Mehrere Referenzmuster pro Klasse
Referenzmuster
Klasse A:
Referenzmuster
Klasse B:
Zu klassifizierende
Testmuster:
Klasse B
Klasse A
Klasse A
?
Abstandsmaß: Absoluter (quadrierter) Abstand zum Klassenmittelwert
Signalverarbeitung 2
Volker Stahl
-5-
Beobachtung:
Wahl der Referenzmuster ist „zufällig“.
Streuung (Varianz) in Klasse A ist kleiner als in Klasse B.
„Wahrscheinlichkeitsdichte“
Signalverarbeitung 2
Volker Stahl
-6-
„Wahrscheinlichkeitsdichte“
Klasse B
Klasse A
Klasse B
62 muss als B klassifiziert werden, obwohl 62 näher beim Mittelwert von A liegt!
Signalverarbeitung 2
Volker Stahl
-7-
Empirischer Mittelwert, empirische Varianz
Stichprobe von Referenzmustern einer Klasse
Ziel: Schätzung der zugrundeliegenden Wahrscheinlichkeitsverteilung
Empirischer Mittelwert
Durchschnitt über alle Beobachtungen
Empirische Varianz
Maß für Streuung, mittlere quadratische Abweichung vom Mittelwert
Signalverarbeitung 2
Volker Stahl
-8-
Klasse A:
Signalverarbeitung 2
Klasse B:
Volker Stahl
-9-
Mahalanobis Abstand
Bisheriges Abstandsmaß: Quadratischer Abstand zum Klassenmittelwert
Ziel: „Besseres“ Abstandsmaß, das die Varianz einer Klasse berücksichtigt
Mahalanobis Abstand:
Intuition:
Varianz einer Klasse groß
Stichprobenelemente streuen stark
quadratischen Abstand zum Mittelwert heruntergewichten!
Signalverarbeitung 2
Volker Stahl
- 10 -
Klassifikation mit Mahalanobis Abstand
Klasse A:
Klasse B:
Abstand zu Klasse A
Abstand zu Klasse B
Klasse B
Klasse B ???
Klasse B
„Fehlklassifikation“ mit Mahalanobis Abstand!
Signalverarbeitung 2
Volker Stahl
- 11 -
Wahrscheinlichkeitsdichte
Klasse B
Signalverarbeitung 2
Klasse A
Klasse B
Volker Stahl
- 12 -
Dichtefunktion der Normalverteilung
Intuition:
Je größer der Wert der Dichtefunktion bei x ist,
desto wahrscheinlicher wird x beobachtet
Großer Wert der Dichte
Signalverarbeitung 2
Kleiner Abstand
Volker Stahl
- 13 -
Abstandsmaß: Negativer Logarithmus der Dichte
Großer Wert der Dichte
Kleiner Abstand
Abstand
Signalverarbeitung 2
Volker Stahl
- 14 -
Abstandsmaß basierend auf Normalverteilung
Mahalanobis
Abstand
Signalverarbeitung 2
Volker Stahl
- 15 -
Klassifikationsergebnis mit Normalverteilungsannahme
Klasse A:
Klasse B:
Klasse B
Klasse A
Klasse B
Signalverarbeitung 2
Volker Stahl
- 16 -
Vereinfachung des Abstandsmaßes: Nur relative Abstände entscheidend!
Klassifikationsergebnis ändert sich nicht,
wenn alle Abstände verdoppelt werden.
Klassifikationsergebnis ändert sich nicht,
wenn von allen Abständen eine Konstante subtrahiert wird.
Korrekturterm
Signalverarbeitung 2
Mahalanobis
Abstand
Volker Stahl
- 17 -
Andere Wahrscheinlichkeitsdichte: Gleichverteilung
Beispiel: Aufenthaltsort eines verlorenen Schlüssels auf dem Heimweg.
Signalverarbeitung 2
Volker Stahl
- 18 -
Andere Wahrscheinlichkeitsdichte: Exponentialverteilung
Beispiel: Wartezeit beim Zahnarzt.
Signalverarbeitung 2
Volker Stahl
- 19 -
Forderungen an eine Dichtefunktion f(x)
Signalverarbeitung 2
Volker Stahl
- 20 -
Zufallsvariablen
„Variable“, die einen Wert zufällig gemäß einer
gegebenen Wahrscheinlichkeitsdichte annimmt: Modell für Unsicherheit.
Notation: Zufallsvariablen werden groß geschrieben.
Mit Zufallsvariablen kann gerechnet werden wie mit gewöhnlichen Variablen.
Rechenoperation auf einer Zufallsvariablen
Rechenoperation auf ihrer Dichte.
Wahrscheinlichkeit, dass eine stetige Zufallsvariable X
exakt den Wert c annimmt:
Probability
Signalverarbeitung 2
Volker Stahl
- 21 -
Wahrscheinlichkeit, dass X einen Wert kleiner oder gleich c annimmt:
: Dichtefunktion
: Verteilungsfunktion
Wahrscheinlichkeit = Fläche unter der Dichtefunktion
Signalverarbeitung 2
Volker Stahl
- 22 -
Wahrscheinlichkeit, dass X einen Wert größer oder gleich c annimmt:
Signalverarbeitung 2
Volker Stahl
- 23 -
Wahrscheinlichkeit, dass X einen Wert zwischen a und b annimmt:
Signalverarbeitung 2
Volker Stahl
- 24 -
Wahrscheinlichkeit, dass X einen Wert zwischen x und x+dx annimmt:
Signalverarbeitung 2
Volker Stahl
- 25 -
Erwartungswert einer Zufallsvariablen
(vgl. empirischer Mittelwert wenn nur eine Stichprobe vorliegt
und die Dichte unbekannt ist)
Varianz einer Zufallsvariablen
(vgl. empirische Varianz wenn nur eine Stichprobe vorliegt
und die Dichte unbekannt ist)
Signalverarbeitung 2
Volker Stahl
- 26 -
Verallgemeinerung auf Zufallsvektoren
Stichprobe von Referenzvektoren einer Klasse
Empirischer Mittelwert, empirische Varianz
Mittelwertvektor, Varianzvektor
Signalverarbeitung 2
Volker Stahl
- 27 -
Zufallsvektor mit Komponenten X und Y
Dichte von X und Y
Annahme: X und Y voneinander unabhängig
unabhängig!
Gemeinsame Dichte von X und Y
Signalverarbeitung 2
Volker Stahl
- 28 -
Signalverarbeitung 2
Volker Stahl
- 29 -
n-stelliger Zufallsvektor
Gemeinsame Dichte falls Komponenten voneinander unabhängig sind.
Signalverarbeitung 2
Volker Stahl
- 30 -
Abstandsmaß mit Normalverteilungsannahme und
Annahme unabhängiger Komponenten
Signalverarbeitung 2
Volker Stahl
- 31 -
Anwendung auf Viterbi Training
und Klassifikation
Ziel: Besseres Modell für die Klassifikation von Merkmalvektorfolgen
Beispiel
Länge 6
Referenzmuster
einer Klasse
(gegeben)
Länge 7
Modell
für die Klasse
(gesucht)
Signalverarbeitung 2
Länge 3
Volker Stahl
- 32 -
Lineare Segmentierung
Modellzustände
Modellzustände
Signalverarbeitung 2
Volker Stahl
- 33 -
Initiale Schätzung der Modellzustände
Signalverarbeitung 2
Volker Stahl
- 34 -
Matchen der Referenzfolgen gegen das Modell mit Viterbi Algorithmus
(Abstandsberechnung mit Varianzen!)
Modellzustände
Modellzustände
Signalverarbeitung 2
Volker Stahl
- 35 -
Neuschätzung der Modellzustände
Iteriere:
Matching mit neuem Modell (Viterbi Algorithmus)
Modell schätzen aus neuer Zuordnung
Signalverarbeitung 2
Volker Stahl
- 36 -
Signalverarbeitung 2
Volker Stahl
- 37 -