Donnerstag 11.4.2013

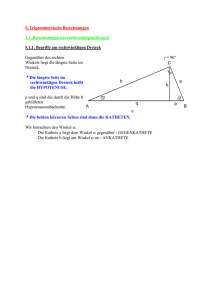
Mathematische Probleme, SS 2013
Donnerstag 11.4
$Id: dreieck.tex,v 1.3 2013/04/12 15:30:18 hk Exp hk $
§1
Dreiecke
1.2
Der Strahlensatz
Nachdem wir in der letzten Sitzung rechtwinklige Dreiecke betrachtet haben, kommen
wir nun zur Einführung der trigonometrischen Funktionen. Als eine kleine Vorbereitung
hierzu, wollen wir erst einmal an den sogenannten Strahlensatz erinnern.
C’
B’
C
B
A
Sind ABC, AB 0 C 0 jeweils kollinear und BB 0 parallel zu CC 0 , so gelten die drei Strahlensätze
|AC|
|AC 0 | |CC 0 |
|BB 0 |
|AC| |CC 0 |
=
,
=
,
=
.
|AB|
|AB 0 | |BB 0 |
|AB| |AC|
|AB|
Die drei Strahlensätzes gehen auf den Begründer der griechischen Mathematik Thales
zurück, dieser war der Lehrer von Pythagoras und lebte geschätzt im Zeitraum 640-546
vor Christus. Thales werden viele Entdeckungen innerhalb und außerhalb der Mathematik zugeschrieben, zum Beispiel war er der erste Mensch der eine Sonnenfinsternis
vorausgesagt hat, nämlich die im Jahre 585 vor Christus. Auch das klassische Beispiel
zur Anwendung der Strahlensätze wurde von Thales selbst beschrieben, es handelt sich
um die Bestimmung der Höhe der Cheops-Pyramide. Wie schon gesagt geschah dies
irgendwann um 600 vor Christus herum, und in dieser Zeit standen keine hierfür hilfreichen technischen Gerätschaften zur Verfügung, Thales musste sich also etwas einfallen
lassen, und das von ihm gewählte Vorgehen soll nun besprochen werden.
2-1
Mathematische Probleme, SS 2013
Donnerstag 11.4
h
l
w
s
S
Zuerst wird die Kantenlänge s der Pyramide vermessen, dies ist leicht machbar und
als das Ergebnis der Messung ergibt sich s = 230m. Als nächster Schritt wird dann der
von der Pyramide geworfene Schatten vermessen, die Gesamtlänge S von Pyramide und
Schatten ergibt sich dann als S = 348m. Diese beiden Werte reichen aber noch nicht aus
die Höhe h der Pyramide zu ermitteln, wir brauchen noch zwei weitere Informationen.
Zu diesem Zweck wird ein mitgebrachter Stab der bekannten Länge l = 1m senkrecht
auf den Boden gestellt und der von diesem Stab geworfene Schatten w gemessen, das
Ergebnis sei w = 1.6m. Diese vier Zahlen s, S, l, w sind jetzt alles was gebraucht wird
um h zu bestimmen. Der Schatten der Cheops-Pyramide entsteht durch den von der
Pyramide verdeckten Teil des Sonnenlichts, sein Ende ist also gerade der Punkt in dem
der durch die Spitze der Pyramide laufende Sonnenstrahl auf den Boden trifft. Da die
Sonnenstrahlen, zumindest in guter Näherung, parallel sind spielt es keine Rolle wo
genau wir den Schatten unseres Stabes messen, wir können uns also den Stab und
seinen Schatten wie im obigen Bild in die Spitze des Schattens der Cheops-Pyramide
verschoben denken. Dann können wir den Strahlensatz anwenden und erhalten
h
S−
s
2
=
h
233m
l
also
=
= 145.625
w
1m
1.6m
und insgesamt ist damit
h = 146m.
1.3
Die trigonometrischen Funktionen
Damit können wir jetzt zu den trigonometrischen Funktionen als den Grundwerkzeugen der Dreiecksberechnung kommen. Wir betrachten ein rechtwinkliges Dreieck ABC
mit rechten Winkel in C, also γ = π/2 wenn wir die Standardbezeichnungen verwenden. Wir nennen die dem Winkel α, also der Ecke A, gegenüberliegende Seite a die
2-2
Mathematische Probleme, SS 2013
Donnerstag 11.4
Gegenkathete zu A und die an A anliegende Kathete b wird als die Ankathete an A
bezeichnet. Die Hypothenuse ist die Seite c. Mit den drei Seiten können wir sechs
Verhältnisse bilden, und diese sind dann, als Funktionen des Winkels α aufgefasst, die
sechs trigonometrischen Funktionen
Sinus
sin α :=
Gegenkathete
a
= , Secans
Hypothenuse
c
secα :=
Hypothenuse
1
=
,
Gegenkathete
sin α
Cosinus cos α :=
Ankathete
b
Hypothenuse
1
= , Cosecans cscα :=
=
,
Hypothenuse
c
Ankathete
cos α
Tangens tan α :=
Gegenkathete
a
Ankathete
1
= , Cotangens cot α :=
=
.
Ankathete
b
Gegenkathete
tan α
Dabei sind der Secans und der Cosecans eher
C’
ungebräuchlich und auch der Cotangens wird
nur selten verwendet. Diese Größen hängen
C
tatsächlich nur vom Winkel α und nicht vom
speziellen rechtwinkligen Dreieck ABC ab.
Haben wir nämlich ein weiteres rechtwinkliges
Dreieck A0 B 0 C 0 mit Winkel α0 = α, so verschieben wir A0 nach A, nehmen also A0 = A
α
B
B’
an und drehen dann um A so, dass die bei- A
den α begrenzenden Geraden identisch werden. Der Sinus sin α ermittelt in ABC ist dann |BC|/|BA| und sin α ermittelt in AB 0 C 0
ist nach dem Strahlensatz ebenfalls |B 0 C 0 |/|AB 0 | = |BC|/|AB|. Dabei verwenden wir
das die beiden Geraden BB 0 und CC 0 die Gerade CC 0 beide mit dem gleichen Winkel,
nämlich 90◦ , schneiden und somit parallel sind. Zur Begründung der Wohldefiniertheit
der anderen trigonometrischen Funktionen geht man dann analog vor.
Wir wollen an dieser Stelle noch eine weitere kleine Anmerkung machen. Verwenden
wir anstelle des Winkels α den anderen nicht rechten Winkel β, so vertauschen sich
Gegenkathete und Ankathete, also haben wir
sin β = cos α, cos β = sin α, tan β = cot α und cot β = tan α.
Man nennt den Winkel β den Komplementärwinkel zu α und hieraus erklärt sich dann
übrigens auch die Bedeutetung des Co“ in Cosinus, Cotangens und Cosecans, dieses
”
steht für komplementär“, da ja zum Beispiel der Cosinus von α gerade der Sinus
”
des Komplementärwinkels β ist. Um diese Beziehungen in einer Formel auszudrücken,
erinnern wir uns daran das die Winkelsumme in einem Dreieck, wie im untenstehenden
Bild gezeigt, immer gleich 180◦ beziehungsweise π im Bogenmaß ist
α + β + γ = π.
Um dies einzusehen, zieht man eine Parallele L zur Seite AB durch den dritten Eckpunkt C. Oberhalb dieser Tangenten ist dann eine weitere Kopie des Winkels γ. Da
2-3
Mathematische Probleme, SS 2013
Donnerstag 11.4
die Gerade L parallel zu AB ist treffen L und AB die beiden Geraden AC und BC
nach dem Stufenwinkelsatz jeweils im selben Winkel, d.h. oberhalb von L liegen wieder
die Winkel α und β an. Insgesamt füllen α, β, γ also eine volle Halbebene aus und wir
haben α + β + γ = π.
γ
β
α
γ
C
α
α
A
β
α
Stufenwinkelsatz
B
Winkelsumme im Dreieck
In unserem rechtwinkligen Dreieck ist γ = π/2, also wird der Komplementärwinkel zu
β=
π
−α
2
und es ergeben sich
sin
und
tan
π
π
− α = cos α, cos
− α = sin α
2
2
π
2
− α = cot α, cot
π
2
− α = tan α.
Unsere Überlegung zur Winkelsumme in einem Dreieck ergibt insbesondere das die beiden nicht rechten Winkel in einem rechtwinkligen Dreieck beide echt kleiner als 90◦ sind,
und damit sind die trigonometrischen Funktionen nur für Winkel α mit 0 < α < π/2
definiert, da noch größere ja nicht in ein rechtwinkliges Dreieck rein passen. Andererseits wollen wir die trigonometrischen Funktionen zur Berechnung von Dreiecken
benutzen, und in einem allgemeinen Dreieck können auch stumpfe Winkel, also Winkel größer als 90◦ , auftauchen. Auf diese könnten wir den Sinus, den Cosinus und so
weiter dann gar nicht anwenden. Um dieses Problem zu vermeiden, dehnen wir die
Definition der trigonometrischen Funktionen auch auf stumpfe Winkel aus, indem wir
für π/2 < α < π
sin α := sin(π − α) und cos α := − cos(π − α)
setzen. Für rechte Winkel müssen wir dann schließlich noch
sin
π
π
:= 1 und cos := 0
2
2
2-4
Mathematische Probleme, SS 2013
Donnerstag 11.4
definieren. Der Tangens wird dann für π/2 < απ als
tan α :=
sin α
= − tan(π − α)
cos α
eingeführt so, dass die Relation tan α = sin α/ cos α für alle 0 < α < π mit α 6=
π/2 besteht. Die Definition der trigonometrischen Funktionen als Seitenverhältnisse ist
nicht so gut geeignet um die Werte dieser Funktionen graphisch zu sehen. Dies läßt
sich dagegen gut an einem Kreis von Radius 1 tun.
1
sin β
1
sin α
β
π−β
tan α
α
cos β
cos α
Zunächst schauen wir uns einen spitzen Winkel 0 < α < π/2 an, der oben im rechten
Dreieck eingezeichnet ist. Verwenden wir dann zum Ablesen von Sinus und Cosinus
dieses rechtwinklige Dreieck, so hat dieses als Hypothenuse den Radius des Kreises,
also 1, also sind der Sinus sin α die Länge der Gegenkathete und der Cosinus cos α
die Länge der Ankathete, wie eingezeichnet. Auch den Tangens von α können wir an
diesem Bild ablesen, betrachten wir nämlich zusätzlich die ganz rechts eingezeichnete
Tangente am Kreis und verlängern das Dreieck zu dieser Tangente hin, so entsteht ein
weiteres rechtwinkliges Dreieck und in diesem wird die Ankathete an α zum Radius
des Kreises, also 1. Der Tangens tan α ist damit die Länge der Gegenkathete in diesem
Dreieck, also der vom Winkel α auf der Tangente ausgeschnittene Tangentenabschitt,
2-5
Mathematische Probleme, SS 2013
Donnerstag 11.4
wie eingezeichnet. Diese Beobachtung erklärt übrigens auch die Herkunft des Namens
Tangens“, dies steht für Tangente“.
”
”
Auch die Bedeutung von Sinus und Cosinus im Fall eines stumpfen Winkels π/2 <
β < π können wir links im Bild ablesen. In dem ganz links eingezeichneten Dreieck
haben wir den Winkel π − β und die Hypothenuse hat wieder die Länge 1. Damit wird
sin(π − β) zur Länge der Gegenkathete und cos(π − β) zur Länge der Ankathete. Die
Koordinaten des Schnittpunkts des auf dem Kreis gelegenen Eckpunkts des Dreiecks
sind dann x = − cos(π − β) = cos β und y = sin(π − β) = sin β.
1.4
Dreiecksberechnung mit Seiten und Winkeln
Nachdem wir jetzt die trigonometrischen Funktionen bereitgestellt haben, können wir
nun zur sogenannten Dreiecksberechnung, oder Trigonometrie, kommen. Einen jedem
Dreieck ∆ sind diverse numerische Werte zugeordnet, zum Beispiel die drei Seitenlängen
a, b, c, die drei Winkel α, β, γ, die Fläche, die Radien von Innkreis und Umkreis, und
man kann noch einige mehr solcher Zahlen erfinden. Das Problem der Dreiecksberechnung besteht nun darin, dass einige dieser Werte vorgegeben werden, zum Beispiel eine
Seite, der ihr gegenüberliegende Winkel und die Fläche, und dann die folgenden Fragen
gestellt werden:
1. Gibt es überhaupt ein Dreick in dem diese Werte angenommen werden?
2. Wenn es eines gibt, ist dieses dann eindeutig? Mit Eindeutigkeit“ ist dabei immer
”
die Eindeutigkeit bis auf Kongruenz, also bis auf Deckbewegungen, gemeint.
3. Wenn es tatsächlich genau ein solches Dreieck gegen sollte, wir kann man dann
die anderen numerischen Größen des Dreiecks in Termen der gegebenen Werte
ausrechnen?
4. Wie kann man das Dreieck effektiv zeichnen? Zu dieser Frage gibt es dann immer einige Varianten, je nachdem welche Hilfsmittel man zum Zeichnen zulassen
möchte. Man kann beispielsweise Konstruktionen mit Geodreieck“ betrachten,
”
dass also Strecken und Winkel abgetragen werden können, oder auch Konstruk”
tionen mit Zirkel und Lineal“. Bei letzteren sind immer umarkierte Zirkel und
”
Lineal“ gemeint, wir können also nur gegebene Strecken verlängern und Kreise
zeichnen deren Mittelpunkt ein schon gegebener Punkt ist und deren Radius als
eine schon gegebene Strecke definiert ist.
Typischerweise muss man drei Werte vorgeben, und gelegentlich müssen diese dabei
Nebenbedingungen erfüllen. In diesem Abschnitt beschränken wir uns auf die Betrachtung der Seiten und der Winkel. Bis auf einige Ausnahmen bestimmen je drei der sechs
Werte a, b, c, α, β, γ das Dreieck bis auf Kongruenz. Eine offensichtliche Ausnahme ist,
dass die Vorgabe der drei Winkel α, β, γ nicht ausreicht, wir können ein Dreieck ja
beliebig strecken ohne seine Winkel zu verändern. Das ist auch nicht so überraschend,
2-6
Mathematische Probleme, SS 2013
Donnerstag 11.4
da die Winkelsumme 180◦ ist, legen zwei der Winkel den dritten bereits fest, es sind
also in Wahrheit nur zwei Informationen vorgegeben, und das reicht nicht aus.
Wir werden systematisch alle Möglichkeiten durchgehen, geordnet nach der Zahl
vorgegebener Seiten. Der erste Fall ist dann, dass alle drei Seiten a, b, c bekannt sind,
und wir die drei Winkel α, β, γ hieraus ermitteln möchten. Hierzu benötigen wir einen
Zusammenhang zwischen Winkeln und Seitenlängen. Diesen erhält man über die trigonometrischen Funktionen, die aus gutem Grund genau so heißen. In einem allgemeinen
Dreieck sind Sinus und Cosinus allerdings nicht mehr direkt als Seitenverhältnisse ablesbar, dies ist nur in rechtwinkligen Dreiecken so. Der gesuchte Zusammenhang wird
anstelle dessen durch den sogenannten Cosinussatz hergestellt. In Worten besagt dieser,
dass in einem jeden Dreieck das Quadrat einer Seite gleich der Summe der Quadrate
der beiden anderen Seiten minus das doppelte des Produkts aus den beiden anderen
Seiten und dem Cosinus des von diesen eingeschlossenen Winkels ist.
Satz 1.4 (Der Cosinussatz)
Sei ∆ ein Dreick mit Seiten a, b, c und Winkeln α, β, γ in der Standardbezeichnung.
Dann sind
a2 = b2 + c2 − 2bc · cos α,
b2 = a2 + c2 − 2ac · cos β,
c2 = a2 + b2 − 2ab · cos γ.
Beweis: Es reicht aus etwa die erste dieser Gleichungen zu beweisen, die anderen beiden
gehen aus dieser Umbezeichnungen hervor. Liegt dabei in α ein rechter Winkel vor, also
α = π/2, so ist cos α = 0 und unsere Behauptung wird zum Satz des Pythagoras Satz
1. Wir können also annehmen das in α kein rechter Winkel ist, d.h. α 6= π/2. Nun
können drei verschiedene Fälle auftreten.
b
α
a
h
b
h
a
α
p
c
Fall 1
p
c
Fall 2
h
a
b
p
α
c
Fall 3
Im ersten Fall ist in α ein spitzer Winkel, also 0 < α < π/2 und die links oben
eingezeichnete Höhe h liegt innerhalb des Dreiecks. In rechtwinkligen Dreieck links von
h liefert der Satz des Pythagoras Satz 1 zunächst b2 = p2 + h2 , wobei p der durch die
Höhe gebildete Abschnitt der Dreiecksseite AB ist, und damit h2 = b2 − p2 . Außerdem
entnehmen wir diesem rechtwinkligen Dreieck noch die Beziehung
p
cos α = , also p = b · cos α.
b
2-7
Mathematische Probleme, SS 2013
Donnerstag 11.4
Eine weitere Anwendung des Satzes von Pythagoras Satz 1 diesmal im Dreieck rechts
von h liefert
a2 = h2 + (c − p)2 = b2 − p2 + (c − p)2 = b2 + c2 − 2pc = b2 + c2 − 2bc · cos α.
Damit ist der Cosinussatz in diesem Fall bewiesen und die anderen beiden Fälle sind
eine Übungsaufgabe.
Ausgerüstet mit dem Cosinussatz können wir jetzt die erste Variante einer Dreiecksberechnung durchführen, nämlich die Dreiecksberechnung bei drei gegebenen Seiten.
Hierbei tritt kein Eindeutigkeitsproblem auf, da wir die Kongruenz von Dreiecken ja
gerade durch die Gleichheit der Seiten definiert haben, aber ein Existenzproblem. Zu
beliebig vorgegebenen a, b, c > 0 muss es keinesfalls ein Dreieck mit diesen Seitenlänge
geben, denn wie wir gleich sehen werden ist in einem Dreieck die Länge einer jeden
Seite echt kleiner als die Summe der Längen der beiden anderen Seiten. Dies ist gerade
die Dreiecksungleichung in ihrer ursprünglichen, namensgebenden Gestalt.
Satz 1.5 (Dreiecksberechnung bei gegebenen Seiten)
Seien a, b, c > 0 gegeben. Genau dann existiert ein Dreieck ∆ mit den Seitenlängen
a, b, c wenn die Dreiecksungleichungen
a < b + c, b < a + c und c < a + b
erfüllt sind. In diesem Fall ist ∆ bis auf Kongruenz eindeutig bestimmt und die Winkel
in ∆ sind in den Standardbezeichnungen gegeben durch
2
b + c 2 − a2
α = arccos
,
2bc
2
a + c 2 − b2
β = arccos
,
2ac
2
a + b2 − c 2
γ = arccos
.
2ab
Beweis: Für spitze Winkel 0 < α < π/2 ist direkt nach Definition 0 < cos α < 1, also
gilt für beliebiges 0 < α < π stets −1 < cos α < 1. Gibt es nun ein Dreieck ∆ mit
Seitenlängen a, b, c und Winkeln α, β, γ, so ergibt der Cosinussatz Satz 4
a2 = b2 + c2 − 2bc · cos α < b2 + c2 + 2bc = (b + c)2 , also a < b + c.
Analog ergeben sich b < a + c und c < a + b, unsere Bedingungen sind also notwendig für die Existenz eines Dreiecks mit den Seitenlängen a, b, c. Sei nun umgekehrt die
Dreiecksungleichung erfüllt. Nach eventueller Umbenennung können wir c ≥ a, b annehmen. Wähle dann eine Strecke AB der Länge c und bilde Kreis K mit Mittelpunkt
2-8
Mathematische Probleme, SS 2013
Donnerstag 11.4
A und Radius b sowie den Kreis L mit Mittelpunkt B und Radius a. Wegen c ≥ a, b
und c < a + b schneiden sich K und L außerhalb von AB und bezeichnet C einen der
beiden Schnittpunkte, so ist ABC ein Dreieck mit den Seitenlängen a, b, c.
K
L
a
b
B
A
Damit haben wir die Existenzaussage bewiesen. Die Eindeutigkeitsaussage ist, wie
schon oben festgehalten, klar und die Formeln für die drei Winkel folgen aus dem
Cosinussatz Satz 4.
Die effektive Konstruktion eines Dreiecks bei gegebenen a, b, c ist jetzt auch leicht
möglich. Wollen wir dies mit dem Geodreick tun, so berechnen wir zunächst den Winkel
α gemäß der obigen Formel und tragen dann Strecken AB und AC der Längen c und b
im Winkel α zueinander ab. Dies gibt uns das gesuchte Dreieck. Die Konstruktion mit
Zirkel und Lineal wurde im Beweis vorgeführt, man zeichnet die beiden beschriebenen
Kreise K und L mit dem Zirkel ein und wählt dann einen der beiden entstehenden
Schnittpunkte. Zum Abschluß dieser Sitzung schauen wir uns jetzt noch zwei explizite
Beispiele an.
1. Seien a = 6, b = 3 und c = 2. Um zu schauen ob es ein Dreick mit diesen
Seitenlängen gibt müssen wir die Dreiecksungleichung überprüfen. Diese ist hier
aber wegen a = 6 > 2 + 3 = b + c offensichtlich verletzt, es gibt also kein Dreieck
mit diesen Seitenlängen.
2. Nun seien a = 4, b = 2, c = 3. Diesmal sind die Dreiecksungleichungen erfüllt,
es reicht ja offenbar diese für die längste Seite zu verifizieren und hier haben wir
a = 4 < 2+3 = b+c. Es gibt also ein Dreieck mit diesen Seitenlängen. Die Winkel
2-9
Mathematische Probleme, SS 2013
Donnerstag 11.4
in diesem Dreieck ergeben sich jeweils auf zwei Nachkommastellen gerundet als
1
4 + 9 − 16
= arccos −
≈ 104, 48◦ ,
α = arccos
12
4
7
16 + 9 − 4
= arccos ≈ 28, 96◦ ,
β = arccos
24
8
16 + 4 − 9
11
γ = arccos
= arccos
≈ 46, 57◦ .
16
16
2-10