1.7. Drehimpulserhaltung - Poenitz-net

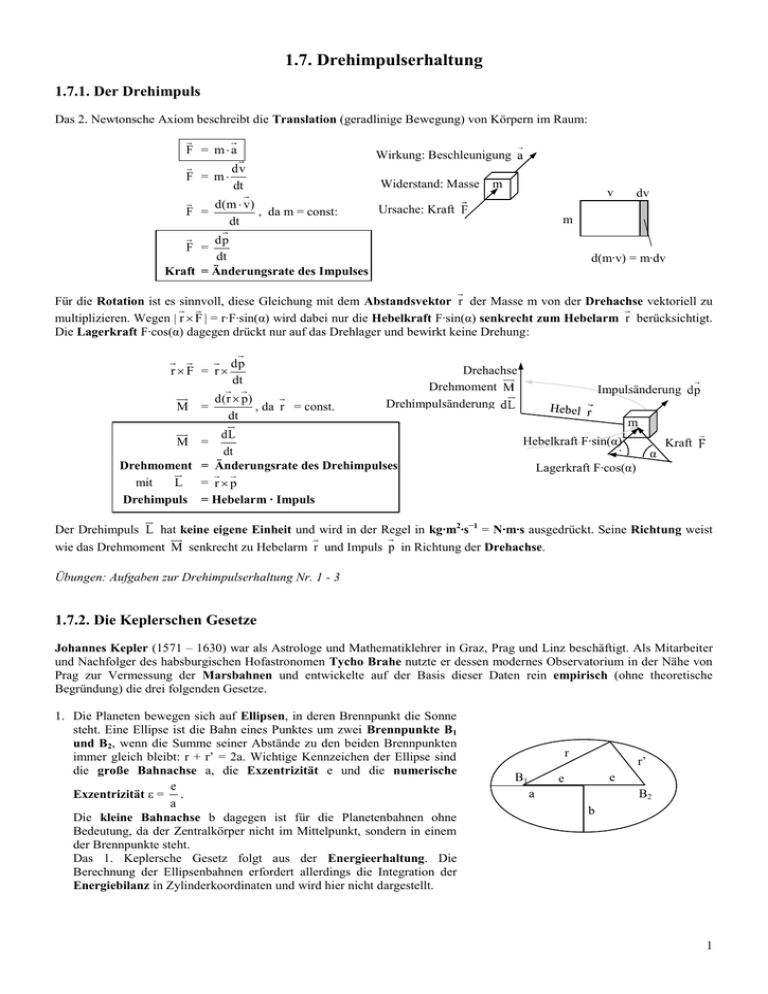
1.7. Drehimpulserhaltung
1.7.1. Der Drehimpuls
Das 2. Newtonsche Axiom beschreibt die Translation (geradlinige Bewegung) von Körpern im Raum:
F = ma
dv
F = m
dt
d(m  v)
, da m = const:
F =
dt
Wirkung: Beschleunigung
Widerstand: Masse
m
v
Ursache: Kraft
dv
m
dp
dt
Kraft = Änderungsrate des Impulses
F =
d(m∙v) = m∙dv
Für die Rotation ist es sinnvoll, diese Gleichung mit dem Abstandsvektor r der Masse m von der Drehachse vektoriell zu
multiplizieren. Wegen | r  F | = r∙F∙sin(α) wird dabei nur die Hebelkraft F∙sin(α) senkrecht zum Hebelarm r berücksichtigt.
Die Lagerkraft F∙cos(α) dagegen drückt nur auf das Drehlager und bewirkt keine Drehung:
rF = r
M =
dp
dt
d(r  p)
, da r = const.
dt
Drehachse
Drehmoment
Drehimpulsänderung
dL
M =
dt
Drehmoment = Änderungsrate des Drehimpulses
mit
L = rp
Drehimpuls = Hebelarm ∙ Impuls
Impulsänderung
m
Hebelkraft F∙sin(α)
∙
Lagerkraft F∙cos(α)
α
Kraft
Der Drehimpuls L hat keine eigene Einheit und wird in der Regel in kg∙m2∙s−1 = N∙m∙s ausgedrückt. Seine Richtung weist
wie das Drehmoment M senkrecht zu Hebelarm r und Impuls p in Richtung der Drehachse.
Übungen: Aufgaben zur Drehimpulserhaltung Nr. 1 - 3
1.7.2. Die Keplerschen Gesetze
Johannes Kepler (1571 – 1630) war als Astrologe und Mathematiklehrer in Graz, Prag und Linz beschäftigt. Als Mitarbeiter
und Nachfolger des habsburgischen Hofastronomen Tycho Brahe nutzte er dessen modernes Observatorium in der Nähe von
Prag zur Vermessung der Marsbahnen und entwickelte auf der Basis dieser Daten rein empirisch (ohne theoretische
Begründung) die drei folgenden Gesetze.
1. Die Planeten bewegen sich auf Ellipsen, in deren Brennpunkt die Sonne
steht. Eine Ellipse ist die Bahn eines Punktes um zwei Brennpunkte B1
und B2, wenn die Summe seiner Abstände zu den beiden Brennpunkten
immer gleich bleibt: r + r’ = 2a. Wichtige Kennzeichen der Ellipse sind
die große Bahnachse a, die Exzentrizität e und die numerische
e
Exzentrizität ε = .
a
Die kleine Bahnachse b dagegen ist für die Planetenbahnen ohne
Bedeutung, da der Zentralkörper nicht im Mittelpunkt, sondern in einem
der Brennpunkte steht.
Das 1. Keplersche Gesetz folgt aus der Energieerhaltung. Die
Berechnung der Ellipsenbahnen erfordert allerdings die Integration der
Energiebilanz in Zylinderkoordinaten und wird hier nicht dargestellt.
r
B1
r’
e
e
a
B2
b
1
2. Der Radiusvektor überstreicht in gleichen Zeiten gleiche Flächen:
L
r  ds
1
=
= const. Diese Gleichung beschreibt die
rv =
2m
2
2dt
dL
des
dt
vorigen Abschnitts: Da kein äußeres Drehmoment M auf die Planeten
dL
wirkt, ist die Änderungsrate
des Drehimpulses gleich Null und der
dt
Drehimpuls L bleibt konstant.
Drehimpulserhaltung und folgt aus der Gleichung M =
a3
= const. Dies folgt für den
T2
Spezialfall der Kreisbahn einfach daraus, dass die Zentripetalkraft Fz gleich der Gravitationskraft FG sein muss:
2
r3
M
M
Mm
 2 
FZ = FG ⇔ m∙ω2r = γ 2 ⇔   r = γ 2 ⇔ 2 =
= const.
T
T
r
r
4
2
 
3. Die Quadrate der Umlaufzeiten verhalten sich wie die Kuben der großen Bahnachsen:
Übungen: Aufgaben zur Drehimpulserhaltung Nr. 5 - 10
1.7.3. Das Trägheitsmoment und die Rotationsenergie
Um die Bewegung eines aus vielen kleinen Massenelementen mi
zusammengesetzten Körpers zu beschreiben, muss man die Summe Σ
der einzelnen Drehmomente M i bzw. Drehimpulse L i bilden:
M
=
i

i
i
dLi
dt
m2
 Mi ist gleich dem gesamten äußeren Drehmoment M , welches
i
z.B. über eine Welle oder als Kräftepaar auf den Körper wirkt. Die
Summe

i
dLi
der Änderungsraten der Drehimpulse ist gleich der
dt
Änderungsrate
dL
des gesamten Drehimpulses.
dt
Sie lässt sich vereinfachen, indem man die bei starren Körpern für alle Massenelemente m i gleiche Winkelgeschwindigkeit ω
ausklammert: Mit L i = r i  pi = r i  (mi  vi ) = r i  (mi  r i  ) = mi  ri2   erhält man  Li =  mi  ri2   = J   mit dem
i
Trägheitsmoment J =
i
 mi  ri2 . Den Wegfall des Kreuzproduktes und der Vektorpfeile sollte man sich mit der Rechtei
Hand-Regel klarmachen! Das Trägheitsmoment J ist ein Ausdruck für den Widerstand, den der Körper dem Drehmoment
entgegensetzt. Man erhält nun für die Rotation eine Gleichung, die dem 2. Newtonschen Axiom für die Translation entspricht.
Der Beschleunigung a =
dv
d
wird dabei durch die Winkelbeschleunigung  =
ersetzt:
dt
dt
Ursache: Drehmoment M
Widerstand: Trägheitsmoment
Wirkung: Winkelbeschleunigung 
M =
dL
dt
= J
J
⇒
d
dt
M = J∙ 
2
Die Rotationsenergie eines mit der Winkelgeschwindigkeit ω rotierenden starren Körpers ist die Summe der kinetischen
Energie seiner Massenelemente mi im Abstand ri zur Drehachse:
Erot =
1
 2 m v
i
2
i
i
=
1
1
 mi  2 ri2 = 2 J∙ω2.
2 i
1
mv2 übernimmt auch in diesem Fall das Trägheitsmoment J die Rolle der
2
Masse m und das Winkelgeschwindigkeit ω die Stelle der Translationsgeschwindigkeit v.
Im Vergleich zur Translationsenergie Etrans =
Trägheitsmomente werden in kg∙m2 angegeben. Für ihre Berechnung benötigt man
die Integration in Zylinderkoordinaten ähnlich wie beim 1. Keplerschen Gesetz. In
den Formelsammlungen sind die Ergebnisse für die wichtigsten Körper und
verschiedene Drehachsen aufgeführt.
Wenn die Drehachse auf der Symmetrieachse liegt, ergeben sich für einen dünnen
Hohlzylinder, dessen gesamte Masse auf den Radius r konzentriert ist, J = mr2; für
2
1
einen Vollzylinder J =
mr2 und für eine Kugel J =
mr2. Je näher die
5
2
Massenelemente an die Drehachse rücken, desto kleiner wird der wirksame
Hebelarm und desto kleiner wird auch das Trägheitsmoment im Verhältnis zum
Hohlzylinder.
Dreht sich ein Körper um eine Achse, die um die Strecke s vom Schwerpunkt
entfernt ist, so kommt einfach das Trägheitsmoment ms2 der entsprechenden
Punktmasse in der Entfernung s von der Drehachse hinzu (Satz von Steiner).
Ein Stab der Länge l, der ähnlich wie ein Propeller um eine Achse senkrecht zur
1
Längsachse durch die Mitte rotiert, hat das Trägheitsmoment J =
m∙l2. Wird er
12
aber um eines seiner Enden geschleudert, so wächst das Trägheitsmoment auf J‘ = J
2
1
1
 1 1
l
+ ms2 =
m∙l2 + m   =    ml2 = ml2.
3
12
4
2
12


 
r
J = mr2
r
J=
mr2
r
J=
mr2
l/2
Übungen. Aufgaben zur Drehimpulserhaltung Nr. 11 - 17
l
l/2
J=
ml2
J=
ml2
3