5. Drehimpuls, Trägheitsmoment, Rotationsenergie, starrer Körper In

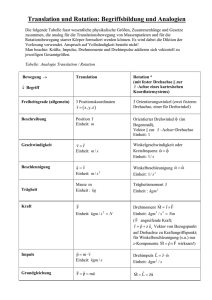
5. Drehimpuls, Trägheitsmoment, Rotationsenergie, starrer Körper
In den Kapiteln 1 bis 4 haben wir nur über Punktmassen, deren Verteilungen und über mögliche
Wechselwirkungen gesprochen.
Hauptziel war die Beschreibung von Bewegungsvorgängen. Wir greifen hier die
Analogiebetrachtungen zwischen Translation und Rotation noch einmal auf und erweitern die Tabelle
in Kapitel 1.4.:
Analogiebetrachtung(en)
Translation
Rotation
Weg s
Geschwindigkeit v
Beschleunigung a
Drehwinkel 
Winkelgeschwindigkeit 
Winkelbeschleunigung 
F Kraft
M Drehmoment
Verknüpfung: Bahngröße = Radius x Winkelgröße (Vektorprodukt!)
Impuls p
Drehimpuls L
Masse m
Kinetische Energie
Trägheitsmoment J (Tensor 2. Stufe)
Rotationsenergie
Ekin 
m 2
v
2
Ekin 
Impulserhaltung
J 2

2
Drehimpulserhaltung
Punktmasse

Masseverteilung

starrer Festkörper
5.1. Der Drehimpuls
Definition:
Lrp
(1)
m
v, p
Mit p  mv laut Gleichung (3), Kapitel 2.3
folgt:
L  r  mv
v  r 
Mit Gleichung (14), Kapitel 1.3 v    r lässt sich bei m  const.
schreiben:
r
L  m  r    r  r  m  r   r   
Mit dem Zerlegungssatz der Vektorrechnung für doppelte Kreuzprodukte formen wir um:

  
a  b  c  c a b  b a  c 
L  m   r  r   r   r  
r
=
0
0
Aufgrund dessen, dass   r steht, lässt sich die Beziehung wesentlich vereinfachen, es bleibt:
L  m  r 2
So
wie
bei
der
(2)
Translation
galt pproportionalv ,
gilt
bei
der
Rotation
nun:
Lproportional  L   .
Der Proportionalitätsfaktor bekommt in Kapitel 5.2 einen eigenen Namen.
5.2 Trägheitsmoment
Der Proportionalitätsfaktor in Gleichung (5.1, 2) lautet: m  r 2
Er beinhaltet Angaben zur Masse des Punktes und auch dessen räumlicher Lage bezüglich des
Drehzentrums.
2
Definition Trägheitsmoment einer Punktmasse J  m  r
(3)
Für Masseverteilungen bzw. ausgedehnte Körper muss über alle Masseelemente summiert werden, um
das Gesamtträgheitsmoment zu erhalten:
mi
N
J   ri 2 dmi   ri 2 mi
(4)
i 1
v
Fällt die Drehachse mit der Schwerpunktachse zusammen,
ist das Gesamtträgheitsmoment eines ausgedehnten Körpers:
ri
J S   r dm
2
(5)
v
Diese Trägheitsmomente sind für sehr viele Körper tabelliert. Bei einer praktischen Anwendung kann
man dort nachschlagen. Allerdings gelten diese Formeln wirklich nur für ausgezeichnete Geometrien
Im allgemeinen Fall ist zu integrieren. Dazu ist je nach Gegebenheit dm in kartesischen, Polar- bzw.
Zylinderkoordinaten oder auch in Kugelkoordinaten aufzuschreiben.
Der folgenden Übersicht ist zu entnehmen, wie die Integrationsvariable in verschiedenen Koordinaten
dargestellt wird sowie auch die Transformationsvorschrift für eine Richtung (die Rücktransformation
ist hier nicht mit angegeben):
Der zweite Einschub enthält einige konkrete Beispiele zur Berechnung von Trägheitsmomenten.
Kugelkoordinaten
Zylinderkoordinaten
Koordinatentransformation (Hinrichtung):
Volumenelement:
Funktionaldeterminante:
Kugel:
Polarkoordinaten:
Zylinder:
Beispiele für die Berechnung von Trägheitsmomenten:
dünner Stab (Masse
, Länge , homogene Dichte ):
1.) a ) Drehachse in der Mitte und geht durch den SP; Querdrehung
Da die Länge des Stabes viel größer als die Dicke und Breite ist, kann wie folgt vereinfacht
werden:
Die Querschnittsfläche
ist konstant und wird vor das Integral gezogen:
Da für die Masse des Körpers gilt:
vereinfacht sich das Ergebnis zu:
1.) b) Jetzt befindet sich die Drehachse am Stabende; Querdrehung
Es gilt die gleiche Vereinfachung, da es sich um den gleichen Stab handelt. Allerdings ist nun
die Drehachse am Ende des Stabes, daher ändern sich die Grenzen des Integrals:
Das
Mit
kann wieder vorgezogen werden, anschließend wird das Integral gelöst:
ergibt sich schließlich:
1.) c) Berechnung für einen dünnen Stab (dünn heißt: Länge L sehr viel größer als der
Durchmesser d)mit der Drehachse irgendwo auf der horizontalen x-Achse und ein
zweiatomiges Molekül
Massen-Trägheitsmomente für einige Geometrien
Berechnung des Massenträgheitsmomentes am Beispiel des Zylinders
Träghe
itsmoment der homogenen Vollkugel
Um das Trägheitsmoment einer massiven homogenen Kugel bezüglich einer Drehachse durch
den Kugelmittelpunkt zu berechnen, wird das im Abschnitt „Berechnung“ angegebene
Integral verwendet. Der Einfachheit halber soll der Kugelmittelpunkt im Ursprung eines
kartesischen Koordinatensystems liegen und die Drehachse entlang der -Achse verlaufen.
Um das Integral
auszuwerten, empfiehlt es sich statt kartesischen lieber Kugelkoordinaten zu verwenden.
Beim Übergang müssen dabei die kartesischen Koordinaten x, y, z und das Volumenelement
dV durch die Kugelkoordinaten
ausgedrückt werden.
Einsetzen in den Ausdruck für das Trägheitsmoment liefert
Hier zeigt sich der Vorteil der Kugelkoordinaten: Die Integralgrenzen hängen nicht
voneinander ab. Die beiden Integrationen über r und lassen sich daher elementar ausführen.
Das verbleibende Integral in
kann durch partielle Integration mit
gelöst werden:
Für das Trägheitsmoment ergibt sich schließlich:
Bei bekanntem Massenträgheitsmoment bezüglich der Schwerpunktachse JS kann bei Drehachsen
parallel zur SP-Achse das Trägheitsmoment über den Satz von Steiner ermittelt werden:
JA
JS
Die momentane Drehachse verläuft parallel zur
Schwerpunktachse durch den Punkt A.
S
A
A
Mit Hilfe des Satzes von Steiner lässt sich das
Trägheitsmoment JA wie folgt berechnen:
J A  J S  ms 2
(6)
s: Abstand zwischen den beiden Achsen.
Verläuft die Drehachse beliebig durch den Körper, hilft nur die Integration.
5.3. Rotationsenergie
Die kinetische Energie bei der Translation war: Wkin  Ekin
Ekin 
m 2
v
2
Wir nutzen jetzt die bereits gefundenen Analogiebetrachtungen aus:
m  J  v 
Damit folgt:
ERot 
J 2

2
(7)
Bis hierher am 28.01.2016, Ende der 14. Vorlesung
5.4. Starrer Körper
Ein starrer Körper (SK) ist nichts anderes als eine „steife“ Massenverteilung. Es werden Punktmassen
aneinandergefügt, die gegenseitig nicht verschiebbar, also starr sind.
Er hat 6 Freiheitsgrade x, y, z, also 3 für die Translation und ,  ,  für die Rotation.
5.5. Die Bewegungsgleichung
Nach dem 2. Newtonschen Axiom gilt: F  ma
Unter Ausnutzung der Analogiebetrachtungen:
F  M ; m  J  a   folgt sofort
M  J 
(8)
In Worten: Drehmoment = Trägheitsmoment x Winkelbeschleunigung
J: mathematisch ein Tensor (3*3)-Matrix!
5.6. Der Energieerhaltungssatz (EES) der Mechanik für die Drehbewegung
Experiment: Pohl’sche Rollen
h
JS
v
h
0
Zustand 1:
E pot  m  g h (oben nur potentielle Energie)
Zustand 2:
Ekin  ERot 
m 2 JS 2
v  
2
2
(9) (unten nur kinetische Energie)
v : Geschwindigkeit der Translationsbewegung des SP
Die kinetische Energie im Zustand 2 (unten) setzt sich zusammen aus der Translation des
Schwerpunktes und der Rotation des Zylinders um seine Mittelpunktachse.
Nimmt man die momentane Achse, die entlang der Mantellinie verläuft, also direkt am
Berührungspunkt zwischen Zylinder und geneigter Ebene, nimmt der EES mit Hilfe des Steinerschen
Satzes eine einfachere Form an.
mg  h 
JA 2

2
(10)
Das ist für viele praktische Rechenübungen wesentlich angenehmer.
5.7. Der Drehimpulserhaltungssatz
Experiment: Drehschemel + Hanteln
Nach Gleichung (2), Kapitel 5.1 gilt:
L  mr 2
d
dt
L  mr 2  J    M
Gleichung (5), Kapitel 2.3
Wirken keine äußeren Momente auf das abgeschlossene System, gilt M  0 und damit L  const.
Ansonsten ergibt sich der Drehimpuls L als Momentenstoß:
t
L   Mdt
0
Anwendungen: Kreisel
(11)
M L