Translation und Rotation: Begriffsbildung und Analogien
Werbung
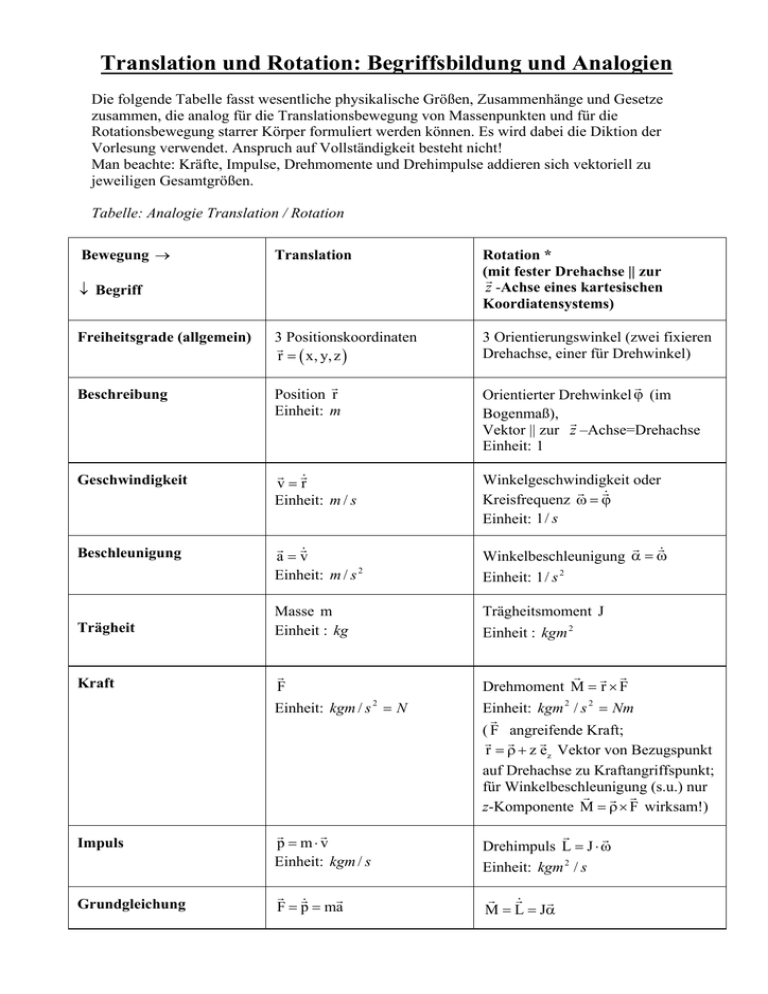
Translation und Rotation: Begriffsbildung und Analogien Die folgende Tabelle fasst wesentliche physikalische Größen, Zusammenhänge und Gesetze zusammen, die analog für die Translationsbewegung von Massenpunkten und für die Rotationsbewegung starrer Körper formuliert werden können. Es wird dabei die Diktion der Vorlesung verwendet. Anspruch auf Vollständigkeit besteht nicht! Man beachte: Kräfte, Impulse, Drehmomente und Drehimpulse addieren sich vektoriell zu jeweiligen Gesamtgrößen. Tabelle: Analogie Translation / Rotation Bewegung → Translation Rotation * (mit fester Drehachse || zur G z -Achse eines kartesischen Koordiatensystems) 3 Positionskoordinaten G r = ( x, y, z ) 3 Orientierungswinkel (zwei fixieren Drehachse, einer für Drehwinkel) Beschreibung G Position r Einheit: m G Orientierter Drehwinkel ϕ (im Bogenmaß), G Vektor || zur z –Achse=Drehachse Einheit: 1 Geschwindigkeit G G v = r Einheit: m / s Beschleunigung G G a = v Einheit: m / s 2 G G Winkelbeschleunigung α = ω Einheit: 1 / s 2 Trägheit Masse m Einheit : kg Trägheitsmoment J Einheit : kgm 2 Kraft G F Einheit: kgm / s 2 = N G G G Drehmoment M = r × F Einheit: kgm 2 / s 2 = Nm G ( F angreifende Kraft; G G G r = ρ + z ez Vektor von Bezugspunkt auf Drehachse zu Kraftangriffspunkt; für Winkelbeschleunigung (s.u.) nur G G G z-Komponente M = ρ× F wirksam!) Impuls G G p = m⋅v Einheit: kgm / s G G Drehimpuls L = J ⋅ ω Einheit: kgm 2 / s Grundgleichung G G G F = p = ma G G G M = L = Jα ↓ Begriff Freiheitsgrade (allgemein) Winkelgeschwindigkeit oder G G Kreisfrequenz ω = ϕ Einheit: 1 / s Impulssatz Energie geleistete Arbeit / Energieumsatz Zugeführte Leistung (positiv oder negativ!) G G Gesamtimpuls p ges = ∑ pi G G Gesamtdrehimpuls Lges = ∑ Li ohne äußere Kräfte zeitlich konstant (mit Betrag und Richtung!) ohne äußere Drehmomente zeitlich konstant (mit Betrag und Richtung!) Kinetische Energie K = 12 mv 2 Rotationsenergie K rot = 12 Jω2 G G ΔW = F ⋅ Δ r G G ΔW = M ⋅ Δϕ = M z ⋅ Δϕz * G G P = F⋅ v G G P = M ⋅ ω = M z ⋅ ωz * * alle Vektorgrößen der Drehbewegung || zur Drehachse; alle Skalarprodukte = gewöhnliche Produkte (der z-Komponenten); positiv oder negativ!