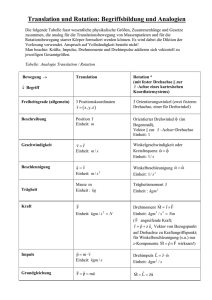
winkelgeschwindigkeit ist die

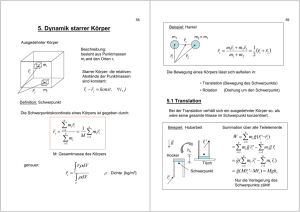
76
5. Dynamik starrer Körper
77
Beispiel: Hantel
m1
Ausgedehnter Körper
Beschreibung:
besteht aus Punktmassen
mi and den Orten ri
r1
rs
m2 = m1
m1r1 + m2 r2 1 rs =
= (r1 + r2 )
2
m1 + m2
r2
mi
ri
Starrer Körper: die relativen
Abstände der Punktmassen
sind konstant:
rj
Die Bewegung eines Körpers lässt sich aufteilen in:
• Translation (Bewegung des Schwerpunkts)
ri − rj = konst . ∀i, j
mj
n
Schwerpunkt:
rs =
∑ mi ri
i =1
n
∑ mi
• Rotation
(Drehung um den Schwerpunkt)
5.1 Translation
=
1
M
n
∑ mi ri
Bei der Translation verhält sich ein ausgedehnter Körper so, als
wäre seine gesamte Masse im Schwerpunkt konzentriert.
i =1
i =1
Kinetische Energie der Translation:
genauer:
r
∫ ρdV
rs = V
∫ ρdV
=
1 2
1
1 2
2
Ekin = ∫ ρ vs + rɺ s dV = M vs + ∫ ρ rɺ s dV
2
2
2
V
V
1 r ρ dV
M V∫
=0 (starrer Körper, keine
Rotation)
V
ρ: Dichte
[kg/m3]
V: Volumen
M: Gesamtmasse
⇒
1
Ekin = M vs
2
2
78
Impuls der Translation:
5.2 Rotation
ɺ
p = ∫ ρ rdV
= ∫ ρ (vs + rɺ s ) dV = vs ∫ ρ dV + ∫ ρ rɺ s dV
V
V
V
Vektorielle Beschreibung der Rotation um den Schwerpunkt
V
p = Mvs
⇒
79
=0
r⊥
Potentielle Energie im Schwerefeld:
E pot
= ∫ ρ ghdV = ∫ ρ rgez dV = gez ∫ ρ rdV = gez Mrs
V
V
V
E pot = Mghs
⇒
Bahngeschwindigkeit:
ω
Die potentielle Energie hängt nur von der vertikalen Lage
des Schwerpunkts ab!
(⇒ der Schwerpunkt ist immer bestrebt, den tiefstmöglichen
Punkt einzunehmen)
α
rs
v =ω×rs
v
Betrag:
v = r s ω sin α
= r⊥ω
Schwerpunkt
r⊥
: Abstand zur Rotationsachse
Kinetische Energie der Rotation
Punktmasse auf Kreisbahn:
1
1
Ekin = mv 2 = mr⊥ 2 ω 2
2
2
J
Beispiel: Hubarbeit
Starrer ausgedehnter Körper:
g
r'
hs
Hocker
Tisch
r
Schwerpunkt
Für die potenteille Energie
ist die Drehung des Hockers
unerheblich; nur die
Verlagerung des
Schwerpunkts hs zählt!
1 2
1
2
Ekin = ∫ ρ v dV = ∫ ρ ω × r s dV
2
2
V
V
1
1
1
= ∫ ρ ( r⊥ω ) 2 dV = ω 2 ∫ ρ r⊥ 2 dV = J ω 2
2
2 V
2
V
J
80
81
Definition: Trägheitsmoment
Masse des gesamten Zylinders:
J = ∫ ρ r⊥ dV
2
V
r0
ρ : Dichte
M = ∫ ρ dV = ∫ ρ 2πr⊥ Ldr⊥ = ρπ r02 L
r⊥ : Abstand zur
V
Rotationsachse
0
L
Damit ist das Trägheitsmoment:
r0
Masse des Zylinders:
Beispiel: Hohlzylinder
J = ∫ ρr dV = ∫ ρr⊥2 2πr⊥ Ldr⊥
2
⊥
M = ∫ ρ dV =ρV ≈ 2π r0 Ld
r0
V
r0
Trägheitsmoment:
Wanddicke d
J = ∫ ρ r⊥2 dV ≈ ∫ ρ r02 dV
L
V
= ρr
∫ dV = ρ r V
2
0
V
Drehachse
J = r02 M
1
1
= 2πρL ∫ r⊥3dr⊥ = 2πρL r04 = Mr02
4
2
0
1
J = r02 M
2
V
2
0
0
r0
V
Das Trägheitsmoment eines massiven Zylinders ist so groß wie
das eines dünnwandigen Hohlszylinders mit gleichem Radius und
halber Masse!
J = ∫ ρ r⊥2 dV
Beispiel: massive Kugel
V
r0
Beispiel: massiver Zylinder
= ∫ ρ r 2π r⊥ 2 r02 − r⊥2 dr⊥
2
⊥
Zur Berechnung von J wird der Zylinder in Hohlzylinder mit
Radius r⊥, Wanddicke dr⊥ und Länge L aufgeteilt.
Volumen der Hohlzylinder:
dV = 2πr⊥ Ldr⊥
V = ∫ dV = ∫ 2πr⊥ Ldr⊥ = π r02 L
V
0
r0
r0
Volumen des gesamten Zylinders:
r0
0
r⊥
2 r02 − r⊥2
= 4πρ ∫ r⊥3 r02 − r⊥2 dr⊥
0
= 4πρ
2 5 2 2 4π 3
r0 = r0 ρ
r0
15
5
3
82
2
J = r02 M
5
Damit:
83
Vergleiche mit gleichförmiger Beschleunigung:
Das Trägheitsmoment einer massiven Kugel ist so groß wie
das eines dünnwandigen Hohlszylinders mit gleichem Radius und
2/5 der Masse!
1 2 v2
s = at =
2
2a
⇒
Experiment: rollende Körper auf schiefer Ebene
s
M
∆h
Körper rollt:
Translation und Rotation!
Zylinder, Kugel,
Radius r0
v
ω=
r0
v
Kreisfrequenz:
α
Kinetische Energie:
M
J
M
J  v  1
J 
= v2 + ω 2 = v2 +   =  M + 2  v2
r0 
2
2
2
2  r0  2 
Mit
wird dies zu
⇒
Mr02
a=
sin α g
Mr02 + J
J = γ Mr02
a=
v = 2as
Beschleunigung
eines rollenden
Körpers auf der
schiefen Ebene
Hohlzylinder:
Vollzylinder:
Kugel:
γ =1
γ =1/ 2
γ =2/5
1
sin α g
1+ γ
2
Ekin
Der Körper sei anfänglich in Ruhe; nach Zurücklegen des Wegs
∆h
sin α
= − ∆ E pot
s=
gilt für die Energien:
Ekin
1
J  2
M
+

 v = Mg ∆h = Mg sin α s
2 
r02 
2 Mr02 J
v=
g sin α s
⇒
Mr02 + J
Die Beschleunigung hängt nicht von der Masse oder dem
Radius ab, sondern nur von der radialen Masseverteilung!
Verhältnis zurückgelegter Strecken:
1
a t2
1 + γ VZ 3
sHZ 2 HZ
=
=
=
sVZ 1 a t 2 1 + γ HZ 4
HZ
2
sVZ 1 + γ K 14
=
=
sK 1 + γ VZ 15
84
85
Beispiel: Garnrolle
5.3 Drehmoment
T = r ×F
Betrachten Balken mit Gewichten
l1
l2
r
Im Gleichgewicht gilt:
F1l1 = F2l2
F2
F1
(Hebelgesetz: Hebelkraft mal
Hebellänge ist konstant)
Faden
l1⊥
β
l1
F1
Es zählt die Hebellänge senkrecht
zur Kraft
l2 ⊥
F
l2
F2
T = r ×F
r
F1l1⊥ = F2l2⊥
α
zeigt in die Papierebene:
Rolle rollt nach rechts
T
momentane
Drehachse
Faden
Genauer:
F
zeigt aus der Papierebene:
Rolle rollt nach links
T
F1l1 sin β = F2l2 sin α
Faden
vektoriell:
F
r
l1 × F1 = l2 × F2
Grenzfall:
T =r×F =0
Es wirkt kein Drehmoment!
Die Rolle kann nur
rutschend gezogen werden
Definition: Drehmoment
T = r ×F
r
in Bezug auf
den Drehpunkt
Einheit: [Nm]
Ein auf einen Körper wirkendes Drehmoment führt zur Rotation.
Beispiel: stabiler Stand
Klotz
g
Schwerpunkt
Stabiles Gleichgewicht bedeutet:
eine kleine Auslenkung erzeugt
eine Gegenkraft (bzw. ein
Gegendrehmoment)
86
87
5.4 Winkelbeschleunigung
g
r
Fg
T
Drehachse
T
T = r ×F
Analog gilt bei der Rotation (um eine feste Drehachse)
1 J
Winkelbeschleunigung
ωɺ = ϕɺɺ = T
dreht daher den Klotz zurück in die
Senkrechte
r Fg
g
Die Gewichtskraft greift am
Schwerpunkt an; das Drehmoment
1 a = ɺɺ
r= F
m
Bei der Translation gilt:
1
J
φɺɺ = T
Beträge:
Drehachse
Außer bei großen Auslenkungen:
g
r Fg
Der Schwerpunkt liegt jenseits
der Drehachse; das Drehmoment
verstärkt das Kippen.
Beispiel: betrachten Punktmasse auf Kreisbahn
F
m
T
r
Ein Körper steht stabil, wenn sich sein Schwerpunkt über seiner
Standfläche befindet!
Gleichgewichte:
Änderung der Bahngeschwindigkeit:
labil: Auslenkung verstärkt
auslenkende Kraft
indifferent: Keine Kraft bei
Auslenkung
Mit
ϕ
stabil: Auslenkung erzeugt
Gegenkraft
⇒
vɺ = a =
v = rω = rϕɺ
rϕɺɺ =
ϕɺɺ =
1
F
m
1
F
m
1
r
T
F= 2 F=
rm
r m
J
:
88
89
5.6 Vergleich Translation/Rotation
5.5 Drehimpuls
p = mv
pɺ = F
Bei der Translation gilt:
Impuls
Impulsänderung
Analog gilt bei der Rotation (um eine feste Drehachse)
l = Jω
lɺ = T
Drehimpuls
Translation
Rotation
Orts-Koordinate
r
Geschwindigkeit
v = rɺ
Masse
Kraft
Impuls
Drehimpulsänderung
m
F
p = mv = mrɺ
t
p = p0 + ∫ Fdt
ϕ
Winkel
ɺ
ω =φ
Winkelgeschw.
Trägheitsmoment
Drehmoment
Drehimpuls
J
T
l = Jω = Jϕɺ
t l = l0 + ∫ Tdt
0
Beispiel: betrachten Punktmasse auf Kreisbahn
F
Es gilt
m
r
ϕ
⇒
T
ϕɺɺ = ωɺ =
J
J ωɺ = lɺ = T
Vektoriell geschrieben und über
die Zeit integriert:
0
Nachrechnen (Beträge):
Arbeit
M 2
vs
2
W = ∫ Fds
E=
Beschleunigung
t l = l0 + ∫ Tdt
Weiterhin gilt hier:
kin. Energie
l = r × p = m r ×v
l = rp = rmv = rmrω = J ω
F
a=
M
(φ )
0
kin. Energie
Arbeit
J 2
ω
2
W = ∫ T dϕ
E=
Winkelbeschleunigung
ɺɺ T
ϕ=
J
90
Die Schwingungsfrequenz eines Fadenpendels im Fall kleiner
Auslenkung ist damit:
Beispiel: Fadenpendel
ϕ
l
also
ω=
T = r ×F g
Das Drehmoment ist
sin ϕ ≈ ϕ
T = −lFgϕ
Für kleine ϕ gilt:
und damit
Das Trägheitsmoment ist
Die Frequenz hängt nur von der Pendellänge ab, nicht von der
Masse!
Zahlenwerte:
J = ml 2
Sekundenpendel (f = 1/s)
l = 0.248 m
2-Sekundenpendel (f = 0.5 1/s) l = 0.99 m
Pendel lassen sich zur Messung von g einsetzen!
Für die Winkelbeschleunigung gilt damit:
ϕɺɺ =
g
l
T = − rFg sin ϕ = −lFg sin ϕ
m
Fg
91
T − lmg
g
=
ϕ
=
−
ϕ
J
ml 2
l
5.5 Steinerscher Satz
Lösungsansatz für diese Differentialgleichung:
Bei Rotation eines Körpers um eine Achse, die nicht durch
den Schwerpunkt führt, gilt für das Trägheitsmoment:
ϕ (t ) = ϕ0 sin(ωt )
g
l
ϕ0ω 2 (− sin(ωt )) = − ϕ0 sin(ωt )
Einsetzen:
⇒
g
ω =
l
2
⇒
ω=
Drehachse
g
l
J = J s + Ma 2
Js : Trägheitsmoment um Schwerpunkt
a
Unter dieser Bedingung erfüllt das angenommene ϕ(t)
die Differentialgleichung.
M : Gesamtmasse
a : Abstand des Schwerpunkts zur Achse
Schwerpunkt
92
93
Trägheitsmoment um den Drehpunkt:
Begrüdung über die kinetische Energie:
2
l 4 l
J = Js + M   = M  
2 3  2
1
1
Ekin = J ω 2 = ( J s + Ma 2 ) ω 2
2
2
Differentialgleichung:
1
1
1
1
= J sω 2 + M (aω ) 2 = J sω 2 + Mvs 2
2
2
2
2
kin. Energie
der Rotation
um Schwerpkt.
l
T
2 ϕ = −3 gϕ
ϕɺɺ = =
J 4  l 2
2l
M 
3 2
− Mg
kin. Energie
der Translation
des Schwerpkts.
Die Aufteilung des Trägheitmoments entspricht der
Auftelung der kinetischen Energie in Rotation und Translation.
ω=
⇒
Zahlenwert:
Beispiel: Stabpendel
Drehpunkt
Trägheitsmoment des Stabs um seinen
Schwerpunkt:
l
ϕ
m/2
l/2
0
0
J s = 2 ∫ r 2 dm = 2 ∫ r 2 ρAdr
Schwerpunkt
Fg
2
l = 1m
3g
2l
⇒
ω = 3.9 1/s; f = 0.6 1/s
5.8 Drehimpulserhaltung
In einem System, auf das kein äußeres Drehmoment wirkt, ist der
Gesamtdrehimpuls eine Erhaltungsgröße.
n l ges = ∑ li = konstant
i =1
mit Dichte ρ und Querschnittsfläche A
M l
1 l3
1 l 
J s = 2 ρA
= ρAl   =  
38
3 2 
3 2
2
2
Beispiel: Rotation mit veränderlichem J
ω
m
r
J = 2mr 2
L = Jω
94
2. Fall:
ω
J ' = 2mr '
m
2
lD = 0
L' = J 'ω ' = L = Jω
r‘
⇒
lR
lD
Rad
J
r2
ω' = ω = 2 ω
J'
r'
Eine Verringerung des Trägheitsmoments beschleunigt die Rotation!
95
lges = lR
lR
⇒
Drehachse
(Drehstuhl ruht)
Umkehrung des Rads führt zur Drehung
des Stuhls mit doppeltem Drehimpuls!
Kinetische Energie:
J ' 2 mr '2 r 4 2 r 2 mr 2 2
ω = 2
ω
E' = ω' =
2
2 r '4
r' 2
5.9 Kreisel
Ein Kreisel behält seine Ausrichtung bei, wenn keine Drehmomente
auf ihn wirken (Kreiselkompass!). Wirkt ein Drehmoment auf ihn,
weicht er „senkrecht dazu“ aus.
Die kinetische Energie erhöht sich (die Verringerung des
Trägheitsmoments erfordert Arbeit!).
Genauer: der Drehimpuls ist eine vektorielle Größe
Beispiel: waagerechter Kreisel mit Zusatz-Gewicht
n lges = ∑ li
i =1
r
Beispiel: System aus Drehstuhl und Rad
lD
lR
Rad
Drehachse
1. Fall:
lges = 0
lD
lR
⇒
m
Fg
ω
Drehmoment:
l
T = r × Fg
(T ⊥ l )
T = T = rmg
In der Zeit dt erzeugt dies einen
Drehimpuls von:
dl = Tdt
Umkehrung des Rads dreht
die Drehrichtung des Stuhls!
( dl ⊥ l )
96
97
Von oben betrachtet:
der zusätzliche Drehimpuls
erzeugt
eine Rotation von l
dϕ l
l'
Winkel:
dl
dl
T dt
dϕ = arctan = arctan l
l
dϕ
l⊥ '
Winkeländerung:
l⊥
dϕ =
dl
l
Die Winkelgeschwindigkeit ist dann:
ω=
dφ T rmg
= =
dt l
l
Beispiel: schräger Kreisel im Schwerefeld
Masse
m
h
Drehmoment:
g
ω=
Schwerpunkt
dϕ hmg
=
dt
l
Präzessionsgeschwindigkeit
schräger Kreisel
Die Präzessionsgeschwindigkeit hängt nicht von dem Winkel
des Kreisels ab, sondern nur von seiner Masse und seinem
Drehimpuls!
5.10 Freie Drehung
Das Trägheitsmoment
J eines Körpers hängt von der Richtung
von ω ab.
Im allgemeinen Fall ist J eine Matrix (der Trägheitstensor):
 J11
J =  J 21

J
 31
T = r × Fg
T = hmg sin α
Änderung des Drehimpulses in
der Zeit dt:
dl = Tdt
α
hmg sin α
dt
l sin α
(Präzessionsfrequenz)
Der Kreisel wird durch das Zusatzgewicht nicht aus der Waagerechten
heraus gekippt, sondern präzediert in einer waagerechten Ebene.
Die Präzessionsgeschwindigkeit ist umso größer, je größer das
ausgeübte Drehmoment und je kleiner der Drehimpuls des Kreisels
ist.
l
l⊥
=
Winkelgeschwindigkeit:
Für dt→0 wird dies:
T dt mgr
dϕ = =
dt
l
l
T dt
J12
J 22
J 32
und es gilt:
( dl ⊥ l )
l = Jω
J13 
J 23 

J 33 
98
Das Trägheitsmoment für eine bestimmte Drehachse ist also:
99
Hauptträgheitsachsen
(„freie Achsen“)
J D = JeD
eD : Einheitsvektor (Länge 1) in
Richtung der Drehachse
J3
Schwerpunkt
Die Matrix J ist diagonalisierbar, d.h. hat drei Eigenvektoren
⇒
jeder Körper hat drei Achsen (Hauptträgheitsachsen),
für welche gilt:
l = Jωi = J iωi
(d.h. der Drehimpuls liegt parallel zur Drehachse)
Dies sind die Achsen des minimalen und des maximalen
Trägheitsmoments, sowie ein dritte zu beiden senkrechte
Achse.
Bem: im Allgemeinen ist der Drehimpuls nicht parallel zur
Drehachse!
ω2
l1
ω = ω1 + ω2
l
l2
Nur für
ist
ω1
J1 = J 2
l1 = l2
!
Da der Drehimpuls bei der
freien Rotation erhalten bleibt,
muss sich also die Richtung
der Drehachse ständig ändern!
(Nutation)
Jmax
Jeder Körper hat drei freie
Achsen.
Das richtungsabhängige
Trägheitsmoment eines
beliebigen Körpers läßt
sich durch einen
„Trägheitsellipsoid“
darstellen.
Jmin
Auftragung der inversen Wurzel des Trägheitsmoments
(das Quadrat des Abstands der Fläche zum Ursprung ist
der Kehrwert von J):
freie Achsen
1/ J
Trägheitsellipsoid
(die freien Achsen
des Körpers sind
die Achsen des
Ellipsoids)
Es gilt: stabile Rotation ist nur möglich um die Achsen mit
maximalem oder minimalem J!
Grund: der Abstand der Tangentialfläche auf dem Ellipsoid am
Durchstoßpunkt der Drehachse zum Mittelpunkt ist eine Konstante
der Bewegung. Tangentialflächen mit maximalem und minimalem
Abstand gibt es jeweils nur eine (bei nichtentarteten Eigenwerten
Ji), für Abstände dazwischen gibt es unendlich viele Flächen, d.h.
der Durchstoßpunkt der Drehachse kann auf dem Ellipsoid
wandern.