5. Dynamik starrer Körper

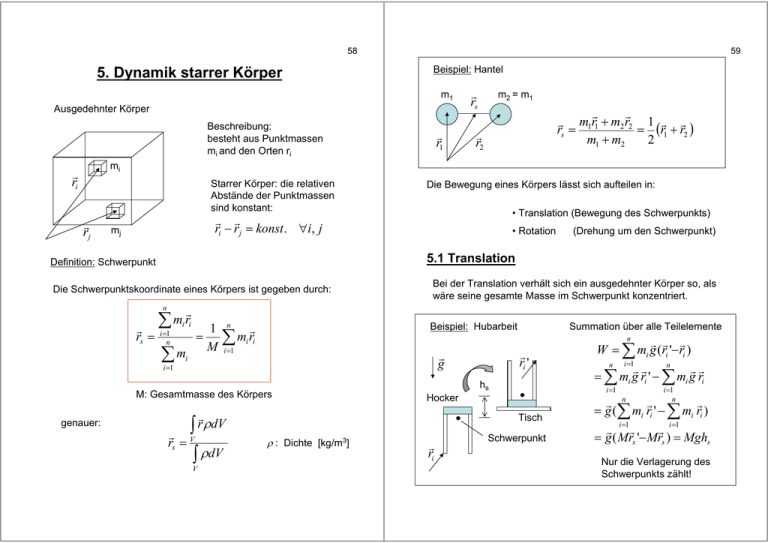
58
5. Dynamik starrer Körper
59
Beispiel: Hantel
m1
Ausgedehnter Körper
Beschreibung:
besteht aus Punktmassen
mi and den Orten ri
r1
rs
m2 = m1
m1r1 + m2 r2 1 rs =
= (r1 + r2 )
2
m1 + m2
r2
mi
ri
Starrer Körper: die relativen
Abstände der Punktmassen
sind konstant:
rj
Die Bewegung eines Körpers lässt sich aufteilen in:
• Translation (Bewegung des Schwerpunkts)
ri − rj = konst . ∀i, j
mj
(Drehung um den Schwerpunkt)
5.1 Translation
Definition: Schwerpunkt
Die Schwerpunktskoordinate eines Körpers ist gegeben durch:
n
rs =
• Rotation
Bei der Translation verhält sich ein ausgedehnter Körper so, als
wäre seine gesamte Masse im Schwerpunkt konzentriert.
∑ mi ri
i =1
n
∑ mi
1
=
M
n
Beispiel: Hubarbeit
∑ mi ri
n
i =1
M: Gesamtmasse des Körpers
hs
rs =
∫V ρdV
n
Tisch
ρ : Dichte [kg/m3]
ri
W = ∑ mi g (ri '− ri )
n
n i =1
= ∑ mi g ri ' − ∑ mi g ri
i =1
Hocker
∫V r ρdV
ri '
g
i =1
genauer:
Summation über alle Teilelemente
Schwerpunkt
i =1
n
= g (∑ mi ri ' − ∑ mi ri )
i =1
i =1
= g ( Mrs '− Mrs ) = Mghs
Nur die Verlagerung des
Schwerpunkts zählt!
60
Kinetische Energie der Translation:
(alle Teilmassen haben dieselbe Geschwindigkeit)
n
1 2 1 2 n
1 2
E = ∑ mi vi = vs ∑ mi = M vs
2
2
i =1 2
i =1
61
ausgedehnter Körper:
n
n
1 2 1
1
2
E = ∑ mi vi = ω 2 ∑ mi r⊥i = Jω 2
2 i =1
2
i =1 2
Definition: Trägheitsmoment
Impuls der Translation:
n P = ∑ mi vi =Mvs
n
J = ∑ mi r⊥i
i =1
i =1
5.2 Rotation
genauer:
J = ∫ r⊥ ρ dV
2
Einschub: vektorielle Beschreibung einer Kreisbewegung
v = −r × ω = ω × r
ω
r⊥
α
r
v
ω
Beispiel: massiver Zylinder
Zur Berechnung von J wird der Zylinder
in Hohlzylinder mit Radius r⊥, Wanddicke dr⊥
und Länge L aufgeteilt.
v = r ω sin α
Volumen der Hohlzylinder:
= r⊥ω
r⊥
ρ : Dichte
V
: Vektor der Winkelgeschwindigkeit
Beträge:
2
dV = 2πr⊥ Ldr⊥
L
: Abstand zur Rotationsachse
Volumen des gesamten Zylinders:
r0
V = ∫ dV = ∫ 2πr⊥ Ldr⊥ = π r02 L
Kinetische Energie der Rotation:
Punktmasse
1
1
2
E = mv 2 = mr⊥ ω 2
2
2
J
r0
Drehachse
V
0
Masse des gesamten Zylinders:
r0
M = ∫ ρ dV = ∫ ρ 2πr⊥ Ldr⊥ = ρπ r02 L
V
0
62
Damit:
63
Beim ausgedehnten Körper gilt:
r0
J = ∫ ρr⊥2 dV = ∫ ρr⊥2 2πr⊥ Ldr⊥
V
r0
n
n l = ∑ r⊥i × pi = ∑ r⊥i × (ri × pi )
0
1
1
= 2πρL ∫ r⊥3dr⊥ = 2πρL r04 = Mr02
4
2
0
i =1
Mit
i =1
a × (b × c ) = (ac )b − (ab )c
gibt dies:
n
2
l = ∑ mi r⊥i ω = Jω
Das Trägheitsmoment eines massiven Zylinders ist so groß wie
das eines dünnwandigen Hohlszylinders mit gleichem Radius und
halber Masse!
i =1
Wichtig: J hängt von der Richtung von
ω
ab!
Impuls der Rotation:
p = mv = mr × ω
J
p = p = mv = mr⊥ω = ω
r⊥
Punktmasse
 J11

J =  J 21
J
 31
r⊥ p = Jω
also
Definition: Drehimpuls
J12
J 22
J 32
und es gilt:
l = Jω
l = r⊥ p = Jω
vektoriell:
Im allgemeinen Fall ist J eine Matrix (der Trägheitstensor):
l = r × p = Jω
(für gegebene Drehachse)
J13 

J 23 
J 33 
64
65
Gleichförmige Winkelbeschleunigung:
5.3 Drehmoment
T = konst.
l = Jω = T t
Betrachten Balken mit Gewichten
b1
b2
Im Gleichgewicht gilt:
F1b1 = F2 b2
F2
F1
(l0 = 0)
Daraus folgt:
1 J
ω = Tt
(Hebelgesetz: Hebelkraft mal
Hebellänge ist konstant)
bzw.
1 J
ωɺ = ϕɺɺ = T
Winkelbeschleunigung
5.4 Vergleich Translation/Rotation
Genauer:
b1⊥
β
b1
F1
Es zählt die Hebellänge senkrecht
zur Kraft
b2 ⊥
F1b1⊥ = F2 b2 ⊥
α
b2
F1b1 sin β = F2 b2 sin α
Rotation
Orts-Koordinate
Masse
Kraft
Impuls
vektoriell:
F2
Translation
b1 × F1 = b2 × F2
r
m
F
p = mv = mrɺ
t
p = p0 + ∫ Fdt
Winkel
ϕ
Trägheitsmoment
J
Drehmoment
Drehimpuls
T
l = Jω = Jϕɺ
t l = l0 + ∫ Tdt
0
Definition: Drehmoment
T = r ×F
r
in Bezug auf
den Drehpunkt
kin. Energie
Arbeit
Zusammenhang mit Drehimpuls:
l = Tt
Genauer:
t l = l0 + ∫ Tdt
0
M 2
vs
2
W = ∫ Fds
E=
Beschleunigung
F
a=
M
0
kin. Energie
Arbeit
J 2
ω
2
W = ∫ T dϕ
E=
Winkelbeschleunigung
ɺɺ T
ϕ=
J
66
67
Anwendungen
Die Schwingungsfrequenz eines Fadenpendels im Fall kleiner
Auslenkung ist damit:
Beispiel: Fadenpendel
ϕ
T = r ×F g
Das Drehmoment ist
l
also
T = − rFg sin ϕ = −lFg sin ϕ
m
Für kleine ϕ gilt:
Fg
und damit
Die Frequenz hängt nur von der Pendellänge ab, nicht von der
Masse!
sin ϕ ≈ ϕ
T = −lFgϕ
Das Trägheitsmoment ist
Zahlenwerte:
J = ml 2
T − lmg
g
=
ϕ =− ϕ
2
J
ml
l
Kinetische Energie nach Weg
s
∆h
m
Lösungsansatz für diese Differentialgleichung:
g
ϕ0ω (− sin(ωt )) = − ϕ0 sin(ωt )
l
g
g
⇒
ω2 =
ω=
l
l
Einsetzen:
⇒
Unter dieser Bedingung erfüllt das angenommene ϕ(t)
die Differentialgleichung.
Ekin =
α
ϕ (t ) = ϕ0 sin(ωt )
2
Sekundenpendel (f = 1/s)
l = 0.248 m
2-Sekundenpendel (f = 0.5 1/s) l = 0.99 m
Beispiel: Zylinder auf schiefer Ebene
Für die Winkelbeschleunigung gilt damit:
ϕɺɺ =
g
l
ω=
Damit gilt:
⇒
s=
m 2 J 2
v + ω = mg∆h
2
2
v = rω
Es ist
m 2 J 2 mr 2 + J 2
v = mgs sin α
v + ω =
2
2
2r 2
v=
2mr 2
g sin α s
mr 2 + J
Vergleiche mit gleichförmiger Beschleunigung:
1 2 v2
s = at =
2
2a
⇒
∆h
sin α
v = 2as
68
Beschleunigung des Zylinders also:
a=
69
5.5 Steinerscher Satz
2
mr
sin α g
mr 2 + J
Bei Rotation eines Körpers um eine Achse, die nicht durch
den Schwerpunkt führt, gilt für das Trägheitsmoment:
J = J s + Ma 2
Diskussion verschiedener Fälle:
1. gesamte Masse im Schwerpunkt:
⇒
J =0
a = sin α g
Js : Trägheitsmoment um Schwerpunkt
M : Gesamtmasse
(altes Ergebnis für schiefe Ebene!)
2. Hohlzylinder:
⇒
3. Massiver Zylinder:
⇒
J = mr 2
1
a = sin α g
2
1
J = mr 2
2
2
a = sin α g
3
a : Abstand des Schwerpunkts zur Achse
Grund: die Bewegung des Körpers läßt sich zerlegen in die
Rotation des Körpers um seinen Schwerpunkt und der Bewegung
des Schwerpunkts auf einer Kreisbahn.
Beispiel: Stabpendel
Drehpunkt
Trägheitsmoment des Stabs um seinen
Schwerpunkt:
l
ϕ
m/2
l/2
J s = 2 ∫ r dm = 2 ∫ r 2 ρAdr
2
Der Hohlzylinder beschleunigt am langsamsten (hier wird nur die
Hälfte der potentiellen Energie in kinetische Energie umgewandelt)
Schwerpunkt
Fg
0
0
mit Dichte ρ und Querschnittsfläche A
2
M l
1 l3
1 l 
J s = 2 ρA
= ρAl   =  
38
3 2 
3 2
2
70
71
ω
Trägheitsmoment um den Drehpunkt:
2
l 4 l
J = Js + M   = M  
2 3  2
L' = J 'ω ' = L = Jω
r‘
Differentialgleichung:
⇒
l
Mg
−
T
2 ϕ = −3 gϕ
ϕɺɺ = =
J 4  l 2
2l
M 
3 2
ω=
⇒
Zahlenwert:
J ' = 2mr '2
m
2
l = 1m
3g
2l
⇒
ω = 3.9 1/s; f = 0.6 1/s
J
r2
ω' = ω = 2 ω
J'
r'
Eine Verringerung des Trägheitsmoments beschleunigt die Rotation!
Kinetische Energie:
J ' 2 mr '2 r 4 2 r 2 mr 2 2
ω = 2
ω
E' = ω' =
2
2 r '4
r' 2
Die kinetische Energie erhöht sich (die Verringerung des
Trägheitsmoments erfordert Arbeit!).
5.7 Kreisel
5.6 Drehimpulserhaltung
In einem System, auf das kein äußeres Drehmoment wirkt, ist der
Gesamtdrehimpuls eine Erhaltungsgröße.
n l ges = ∑ li = konstant
i =1
Ein Kreisel behält seine Ausrichtung bei, wenn keine Drehmomente
auf ihn wirken (Kreiselkompass!). Wirkt ein Drehmoment auf ihn,
weicht er „senkrecht dazu“ aus.
Beispiel: waagerechter Kreisel mit Zusatz-Gewicht
r
Beispiel: Rotation mit veränderlichem J
ω
m
r
J = 2mr 2
L = Jω
m
Fg
ω
l
Drehmoment:
T = r × Fg
(T ⊥ l )
T = T = rmg
In der Zeit dt erzeugt dies einen
Drehimpuls von:
dl = Tdt
( dl ⊥ l )
72
73
Von oben betrachtet:
der zusätzliche Drehimpuls
erzeugt
eine Rotation von l
dϕ l
l'
Winkel:
dl
dl
T dt
dϕ = arctan = arctan l
l
Für dt→0 wird dies:
T dt mgr
dϕ = =
dt
l
l
Die Winkelgeschwindigkeit ist dann:
ω=
dϕ rF rmg
=
=
dt
l
l
(Präzessionsfrequenz)
Der Kreisel wird durch das Zusatzgewicht nicht aus der Waagerechten
heraus gekippt, sondern präzediert in einer waagerechten Ebene.
Die Präzessionsgeschwindigkeit ist umso größer, je größer das
ausgeübte Drehmoment und je kleiner der Drehimpuls des Kreisels
ist.
Beispiel: schräger Kreisel im Schwerefeld
Masse
m
h
l
Drehmoment:
g
T = r × Fg
T = hmg sin α
Änderung des Drehimpulses in
der Zeit dt:
dl = Tdt
α
Schwerpunkt
( dl ⊥ l )
dϕ
l⊥ '
Winkeländerung:
l⊥
dl
l
dϕ =
T dt
l⊥
=
hmg sin α
dt
l sin α
Winkelgeschwindigkeit:
ω=
dϕ hmg
=
dt
l
Präzessionsgeschwindigkeit
schräger Kreisel
Die Präzessionsgeschwindigkeit hängt nicht von dem Winkel
des Kreisels ab, sondern nur von seiner Masse und seinem
Drehimpuls!