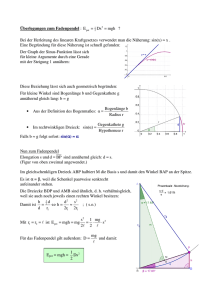
1 Wiederholung: Fadenpendel und mechanische Schwingungen

1 Wiederholung: Fadenpendel und mechanische
Schwingungen
1.1 Ungedämpfter harmonischer Oszillator
Ein Fadenpendel besteht aus einer Masse m, die am
Ende eines Fadens der Länge ` aufgehängt ist. Der Faden wird dabei als masselos und die schwingende Masse
als punktförmig betrachtet, so daß ` im wesentlichen
den Schwerpunktsabstand angibt.
Auf die Masse wirkt ihre Gewichtskraft im Schwerefeld:
G = −m g ey
(1.1)
Diese kann in einen radialen Anteil Grad zerlegt werden, der in Richtung des Fadens zeigt, sowie in einen
tangentialen Anteil Gtan , der in Bahnrichtung zeigt.
Die Kräfte sind in Abb. 1.1 veranschaulicht. Für ihre
Beträge gilt:
Grad = −m g cos θ
Abbildung 1.1 – Das (mathematische) Fadenpendel.
Gtan = −m g sin θ
(1.2)
Dabei beschreibt θ = θ(t) den zeitabhängigen Auslenkungswinkel des Pendelkörpers. Der zurückgelegte Weg des Pendels lässt sich im Bogenmaß berechnen durch
s(t) = ` θ(t)
(1.3)
woraus unmittelbar die auf ihn wirkende Beschleunigung durch
atan (t) =
d2 s
d2 θ
=
`
dt2
dt2
(1.4)
folgt. Für kleine Winkel lässt sich der Sinuswert des Winkels durch seinen Betrag im Bogenmaß
nähern (lineare Näherung), dann gilt sin θ ≈ θ, so daß für die tangentiale Beschleunigung auf
die Masse gilt:
atan (t) ≈ −g θ(t)
(1.5)
Gleichsetzen von Gl. (1.4) und Gl. (1.5) liefert dann eine Bewegungsgleichung für die Pendelmasse, die sog. Differentialgleichung des harmonischen Oszillators:
1
g
d2 θ(t)
= − θ(t)
2
dt
`
(1.6)
Diese kann gelöst mit einem Lösungsansatz
θ(t) = θ0 cos (ωt + φ0 )
(1.7)
mit der Amplitude θ0 , der Kreisfrequenz ω und der Phasenverschiebung φ0 gelöst werden. Einsetzen in Gl. (1.6) liefert dann:
g
− ω θ0 sin (ωt + φ0 ) = − θ0 sin (ωt + φ0 )
`
2
⇐⇒
g
sin (ωt + φ0 ) = 0
ω −
`
2
(1.8)
Da im allgemeinen der Sinus-Ausdruck nur für spezielle Werte von t den Wert 0 annimmt, muß
der geklammerte Ausdruck identisch 0 sein, um die Differentialgleichung zu lösen. Man hat so
die Kreisfrequenz des Oszillators als
r
ω=
g
`
s
=⇒
T = 2π
`
g
(1.9)
bestimmt. Die Amplitude und die Phasenverschiebung folgen, indem man die Anfangsbedingungen
θ(t = 0) = 10
θ̇(t = 0) = 0
(1.10)
in den Ansatz Gl. (1.7) einsetzt und nachrechnet, als θ0 = 10 und φ0 = 0. Die Schwingung ist
durch die blaue Kurve in Abb. 1.2 veranschaulicht.
1.2 Gedämpfter harmonischer Oszillator
Berücksichtigt man zusätzlich die Reibung, die auf die Masse wirkt, so muß auf der rechten Seite
von Gl. (1.6) noch ein Dämpfungsterm
aReib = −2γ
dθ
dt
(1.11)
eingefügt werden. Dabei bezeichnet man γ als Reibungskoeffizienten. Man erhält dann die Differentialgleichung des gedämpften harmonischen Oszillators:
dθ
d2 θ
+ 2γ
+ ω02 θ = 0
2
dt
dt
(1.12)
θ(t) = θ0 e−γt sin (ωged t + φ0 )
(1.13)
Sie wird durch einen Ansatz
2
Abbildung 1.2 – Bewegung eines gedämpften und eines ungedämpften harmonischen Oszillators.
gelöst, die Amplitude fällt also, im Gegensatz zum ungedämpften Oszillator, exponentiell ab (s.
Vergleich der Weg-Zeit-Gesetze in Abb. 1.2). Die Dämpfung beeinflusst auch die Frequenz der
Schwingung, diese nimmt mit zunehmender Dämpfung immer weiter ab, es gilt hierbei:
ωged =
q
ω02 − γ 2
Für schwache Dämpfungen ist dieser Effekt jedoch vernachlässigbar.
3
(1.14)
2 Drehbewegungen
Man betrachtet einen Wägebalken, an dessen einer
Seite ein Gewicht aufgehängt ist, und an dessen anderer Seite eine beliebig gerichtete Kraft ansetzt.
Ausprobieren führt dann schnell zu der Erkenntnis,
daß nur der Kraftanteil, der senkrecht zum Wägebalken steht, hilft, diesen in der horizontalen zu halten. Dieser Kraftanteil bewirkt nämlich ein Drehmoment, welches das durch das Gewichtsstück verursachte Drehmoment kompensiert.
Abbildung 2.1 – Kräfte beim Ziehen an
einer Waage.
2.1 Drehmoment und Drehimpuls
Abb. 2.2 zeigt einen Massenpunkt, der sich an einem Ort r(t) befindet, und auf den eine Kraft F
einwirkt. Diese Kraft entspricht der zeitlichen Änderung seines Impulses,
F=m
dv
dt
(2.1)
Multipliziert man vektoriell auf beiden Seiten der
Gleichung den Ortsvektor r an, so erhält man:
d (r × v)
dt
dr
dv
× v +m r ×
=m
dt
|dt {z }
r×F=m
(2.2)
=0
Abbildung 2.2 – Kraft auf einen Massepunkt
Der erste Term rechts des Gleichheitszeichens entfällt hierbei, da dr
dt = v ist, und das Kreuzprodukt identischer Vektoren den Nullvektor liefert.
Der zweite Term enthält den Drehimpuls L:
L = mr × v = r × p
(2.3)
Den Term links des Gleichheitszeichens nennt man Drehmoment M:
M=r×F
4
(2.4)
Aus dieser Betrachtung folgt auch, daß der Drehimpuls eine Erhaltungsgröße ist. Betrachtet
man erneut Gl. (2.2) und setzt Gln. (2.3), (2.4) ein, so erhält man eine Gleichung analog zum
2. Newton’schen Axiom:
M=
dL
dt
(2.5)
2.2 Trägheitsmoment
Betrachtet man einen Massenpunkt auf einer kreisförmigen Bahn mit Radius r (Ortsvektor r) und der Bahngeschwindigkeit v, so kann ihm die Kreisgeschwindigkeit ω
zugeordnet werden, die durch ω = r × v definiert ist.
Betrachtet man nun einen komplexen Körper, der aus vielen Massepunkten mi aufgebaut ist, die durch Ortsvektoren ri adressiert werden und sich mit Bahngeschwindigkeiten vi bewegen, so ergibt sich für den Drehimpuls dieses
Körpers:
L=
X
mi ri × v =
i
X
Abbildung 2.3 – Veranschaulichung der Kreisgeschwindigkeit.
mi ri × (ω × ri )
i
!
X
=ω
(2.6)
2
mi ri,⊥
i
|
{z
}
=I
Den Ausdruck
I=
X
2
mi ri,⊥
(2.7)
i
bezeichnet man als das Trägheitsmoment des Körpers. Mit ihm lassen sich analog zur Translationsbewegung Rotationsenergie und Drehimpuls schreiben als:
L=Iω
1 2 2 1 2
Erot = mr⊥
ω = Iω
2
2
(2.8)
2.3 Das physikalische Pendel
Für einen ausgedehnten Körper kann man seinen Schwerpunkt (SP) definieren. Lagert man einen
Körper außerhalb seines Schwerpunkts, wie in Abb. 2.4 gezeigt, so führt die im Schwerpunkt
angreifende Gewichtskraft G zu einem Drehmoment um den Drehpunkt (DP). Es gilt dann:
dL
d (IDP ω)
d2 θ
=
= IDP 2
dt
dt
dt
5
(2.9)
In Analogie zum Fadenpendel kann man dann die Bewegungsgleichung für den Körper durch
eine Drehmomentenbilanz aufstellen. Das Drehmoment ist dann gegeben durch:
M = IDP
d2 θ(t)
= r × G = −m g ` sin θ(t) ≈ −m g ` θ(t)
dt2
(2.10)
Dies ist wieder eine Differentialgleichung des harmonischen Oszillators, man löst sie analog zu Gl. (1.6). Für die Kreisfrequenz findet
sich diesmal
s
ω=
mg`
IDP
(2.11)
Hierbei bezeichnet IDP das Trägheitsmoment bezüglich der Drehachse. Dieses lässt sich aus dem Satz von Steiner berechnen:
Abbildung 2.4 – Das
physikalische Pendel.
IDP = ISP + M a2
(2.12)
mit dem Trägheitsmoment bei Rotation um den Schwerpunkt, ISP , der Masse M des Körpers
und dem Abstand a der Verbindungslinie von Dreh- und Schwerpunkt.
2.4 Der Mathieu-Oszillator
Ein interessanter Fall ist nun der, daß man die Gewichtskraft des Körpers “moduliert”. Dies
entspricht dem Ingangsetzen einer Schaukel durch eine ständige Auf- und Abbewegung des
Schaukelnden, also einer Modulation der Schwerpunktlage.
Mathematisch lässt sich dieses Verhalten durch Addition einer modulierten Beschleunigung zum
Schwerefeld erfassen, man erhält die “effektive Schwerkraft”:
geff (t) = g + a sin Ωt
(2.13)
Man erhält dann die Differentialgleichung:
I
d2 θ(t)
dθ(t)
+ 2γ 0
+ m `θ(t) (g + a sin Ωt)
2
dt
dt
(2.14)
Division durch I liefert dann die Differentialgleichung des sog. Mathieu-Oszillators:
a
d2 θ(t)
dθ(t)
+ 2γ
+ ω02 1 + sin Ωt = 0
2
dt
dt
g
(2.15)
mit der Anregungsfrequenz Ω. Diese Differentialgleichung ist analytisch nicht lösbar.
Man kann allerdings für verschiedene Werte der Anregungsfrequenz Ω und der Anregungsamplitude a das Verhalten des Systems auf (In-)stabilität hin untersuchen, die Ergebnisse sind in
Abb. 2.5 zusammengefasst.
6
Anregende Kraft a
instabil
instabil
Anregende Kraft a
stabil
stabil
instabil
Anregende Frequenz
Anregende Frequenz
7Hz
Abbildung 2.5 – Verhalten des Mathieu-Oszillators für verschiedene Anregungen. Links:
Ω/ω0 ≥ 0, Rechts: Ω/ω0 < 0
Es stellt sich heraus, daß für die eine Kombination von Anregungsfrequenz und -amplitude das
System instabil wird. Im instabilen Zustand genügen kleinste Störungen, um das Pendel aus
seiner Ruhelage auszulenken. So gerät es bei Anregung mit ca. 7 Hz ohne Eingreifen durch den
Experimentator in Schwingung. Für noch höhere Frequenzen und Anregungskräfte lässt sich das
Pendel sogar auf den Kopf stellen.
7
Experimente zur
Selbstorganisation
Modelle für den Kosmos und
die belebte Natur
Das Phänomen
Wellen
Wirbel
Aus: www-imk.physik.uni-karlsruhe.de
Wanderdünen
Kosmologische Strukturen
Numerische Simulation der Supernova 1987A
Modell des Urknalls
Chemie und Biologie?
Belousov-Zabatinski
Schleimpilze
(chemische Reaktion)
(Dictyostelium)
Physik und Biologie?
Eiskristalle
(dentritisches Wachstum)
Bakterienkultur
Fragestellung
1.) Verwunderung über regelmäßige,
symmetrische Strukturen in der Natur
2.) Technische Fragestellungen:
Probleme bei der Fertigung (Vermeidung!)
3.) Kann die klassische Wissenschaft der unbelebten Materie bei dem
Verständnis der belebten Natur hilfreich sein?
Tatsache: Belebte Natur neigt zur Strukturbildung
Mechanismen
Zufall
Genetik
Physik. + Chem.
Gesetze
Modelle
Lebensform
Ingredienzen
3 Zutaten
1.) Energieaustausch mit der Umgebung (Antrieb)
2.) Instabilität
Struktur
Kleiner Antrieb: Keine Struktur !!!
Antrieb
3.) Nichtlinearität
bestimmt Musterselektion
B
Starke Nichtlinearität:
Chaos
A
Die Welt schwingt: Das physikalische Pendel
  2  g   0
2
0
Die Welt schwingt: Das physikalische Pendel
  2  g   0
2
0
g   g  a sin t
 a

  2   1  sin t    0
 g

2
0
Der Mathieuoszillator
instabil
instabil
Anregende Kraft a
Die Welt schwingt
stabil
Anregende Frequenz
7Hz
Anregende Kraft a
Die Welt schwingt auf dem Kopf
stabil
instabil
Anregende Frequenz
Wellen:2 Beispiele
Das Faraday Experiment
Lautsprecher
Verstärker
3 Zutaten ?
Frequenzgenerator
Wellen:Theorie
Wellenlänge [m]
Wellenlänge durch antreibende
Frequenz einstellbar
=> Dispersionsrelation
Stehende Wellen
Frequenz [Hz]
Muster:Theorie
Ginsburg Landau Gleichung
N
 t H j   j      ( lj )  l  j
*
l
*
m
2
l
N=1->Linien
N=2->Quadrate
N=3-> hexagones
Wellen:Experimente !!!
Experimenteller Aufbau
LED´s
CCD
DA/AD
glass plate
PC
IEEE
accelerometer
heating filament
PT-100
vibration exciter
max. shaker elongation:
54 mm
max. force:
4200N
container diameter:
290 mm
-> closed loop algorithm at low 
temperature controler
power amplifier
CCD-camera: synchronized
The quantitative determination of the
surface profile
Dye isNiSO4with an
absorption at 6-800nm
N



  H  cos k j x   j *  cos i t 
j 1
i 1