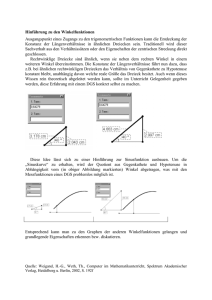
? mgh Ds E = = BP d = i == 1rr

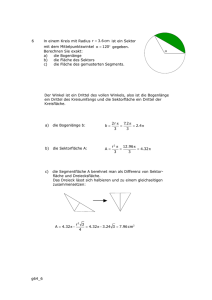
Überlegungen zum Fadenpendel : E pot = 12 Ds 2 = mgh ?
Bei der Herleitung des linearen Kraftgesetzes verwendet man die Näherung: sin(x) ≈ x .
Eine Begründung für diese Näherung ist schnell gefunden:
Der Graph der Sinus-Funktion lässt sich
für kleine Argumente durch eine Gerade
mit der Steigung 1 annähern:
Diese Beziehung lässt sich auch geometrisch begründen:
Für kleine Winkel sind Bogenlänge b und Gegenkathete g
annähernd gleich lang: b ≈ g
•
Aus der Definition des Bogenmaßes: α =
•
Im rechtwinkligen Dreieck: sin(α) =
Bogenlänge b
Radius r
Gegenkathete g
Hypothenuse r
Falls b ≈ g folgt sofort: sin(α) ≈ α
Nun zum Fadenpendel
Elongation s und d = BP sind annähernd gleich: d ≈ s.
(Figur von oben zweimal angewendet.)
Im gleichschenkligen Dreieck ABP halbiert M die Basis s und damit den Winkel BAP an der Spitze.
Es ist α = β, weil die Schenkel paarweise senkrecht
aufeinander stehen.
Die Dreiecke BDP und AMB sind ähnlich, d. h. verhältnisgleich,
weil sie auch noch jeweils einen rechten Winkel besitzen:
h 1d
d 2 s2
≈
; ( s.o.)
Damit ist = 2 ⇔ h =
d
r1
2r1 2r1
Mit r1 = r2 = l ist E pot
s 2 1 mg 2
= mgh = mg = ⋅
⋅s
2l 2 l
Für das Fadenpendel gilt außerdem: D =
Epot = mgh =
1 2
Ds
2
mg
und damit:
l