α α γ γ β β c c b b a a A B C A B C

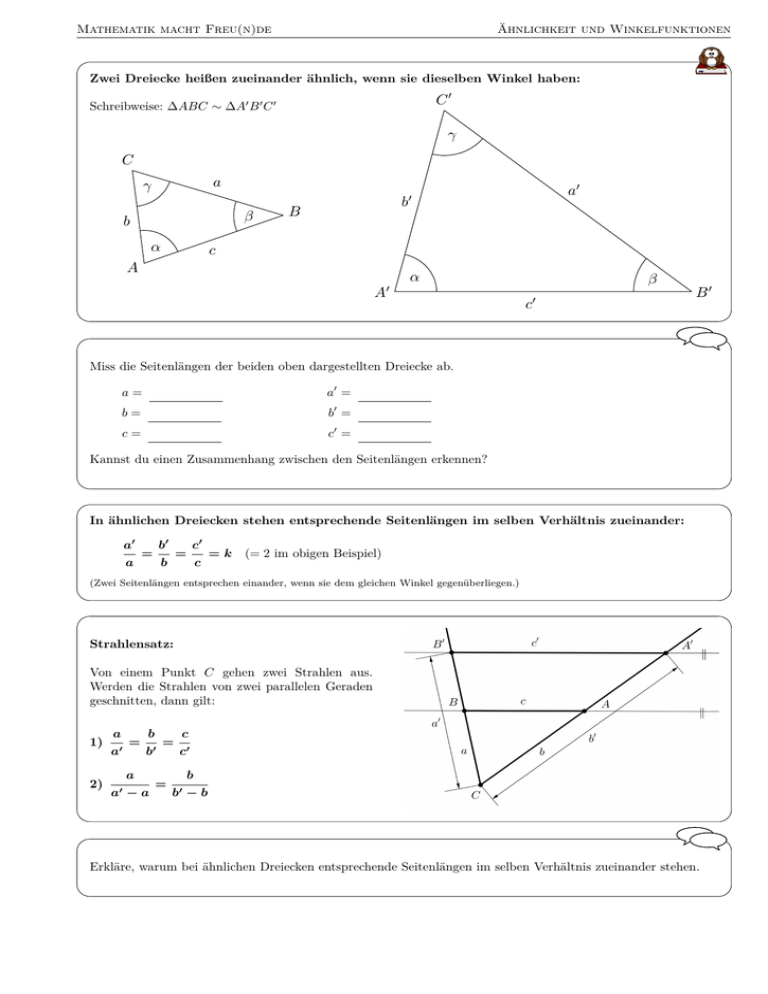
Mathematik macht Freu(n)de
Ähnlichkeit und Winkelfunktionen
Zwei Dreiecke heißen zueinander ähnlich, wenn sie dieselben Winkel haben:
C0
Schreibweise: ∆ABC ∼ ∆A0 B 0 C 0
γ
C
a
γ
β
b
α
a0
b0
B
c
A
α
A0
β
0
c
B0
Miss die Seitenlängen der beiden oben dargestellten Dreiecke ab.
a=
a0 =
b=
b0 =
c=
c0 =
Kannst du einen Zusammenhang zwischen den Seitenlängen erkennen?
In ähnlichen Dreiecken stehen entsprechende Seitenlängen im selben Verhältnis zueinander:
a0
a
b0
=
c0
=
b
c
=k
(= 2 im obigen Beispiel)
(Zwei Seitenlängen entsprechen einander, wenn sie dem gleichen Winkel gegenüberliegen.)
Strahlensatz:
Von einem Punkt C gehen zwei Strahlen aus.
Werden die Strahlen von zwei parallelen Geraden
geschnitten, dann gilt:
1)
2)
a
a0
=
b
b0
a
a0
−a
=
=
c
c0
b
b0
−b
Erkläre, warum bei ähnlichen Dreiecken entsprechende Seitenlängen im selben Verhältnis zueinander stehen.
Mathematik macht Freu(n)de
Ähnlichkeit und Winkelfunktionen
Erkläre, warum zwei rechtwinklige Dreiecke ähnlich zueinander sind, wenn beide den gleichen Winkel α haben:
·
b0
·
b
α
α
c
Erkläre, warum
a0
a
c0
a0
a
= 0 gilt.
c
c
·
b
Kathete a liegt gegenüber von α
=⇒ „Gegenkathete von α“
a
α
Kathete b liegt am Winkel α an
=⇒ „Ankathete von α“
β
c
Erkläre, warum das Seitenverhältnis
·
b
Gegenkathete von α
nur vom Winkel α abhängt.
Hypotenuse
sin(α) =
Gegenkathete von α
Hypotenuse
=
„Sinus von α“
a
cos(α) =
α
β
c
tan(α) =
Ankathete von α
Hypotenuse
„Cosinus von α“
=
Gegenkathete von α
Ankathete von α
=
„Tangens von α“
Wir wählen am Kreis mit Radius 1 („Einheitskreis“) einen Punkt P und zeichnen ein rechtwinkliges Dreieck:
1) Erkläre, warum die Länge der senkrechten Kathete stets sin(α) beträgt,
unabhängig davon wo am Viertelkreisbogen der Punkt P gewählt wird.
2) Wie groß und klein kann sin(α) für spitze Winkel α also höchstens sein?
Die Zuordnung von Winkel zu Seitenverhältnis kann umgekehrt werden:
sin(α) = 0,5 ⇐⇒ α = arcsin (0,5)
„Arcussinus“
cos(α) = 0,5 ⇐⇒ α = arccos (0,5)
„Arcuscosinus“
tan(α) = 0,5 ⇐⇒ α = arctan (0,5)
„Arcustangens“
Dieses Werk von Mathematik macht Freu(n)de unterliegt einer CC BY-NC-ND 4.0 Lizenz.
http://mathematikmachtfreunde.univie.ac.at