g64_6 6 In einem Kreis mit Radius r = 3.6cm ist ein - SOS
Werbung

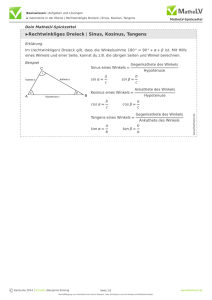
6 In einem Kreis mit Radius r = 3.6 cm ist ein Sektor mit dem Mittelpunktswinkel = 120° gegeben. Berechnen Sie exakt: a) die Bogenlänge b) die Fläche des Sektors c) die Fläche des gemusterten Segments. Der Winkel ist ein Drittel des vollen Winkels, also ist die Bogenlänge ein Drittel des Kreisumfangs und die Sektorfläche ein Drittel der Kreisfläche. a) die Bogenlänge b: b= 2 r 7.2 = = 2.4 3 3 b) die Sektorfläche A: A= r 2 12.96 = = 4.32 3 3 c) die Segmentfläche A berehnet man als Differenz von Sektorfläche und Dreiecksfläche. Das Dreieck lässt sich halbieren und zu einem gleichseitigen zusammensetzen: A = 4.32 g64_6 r2 3 = 4.32 3.24 3 7.96 cm2 4