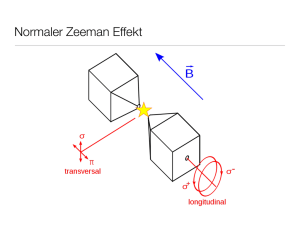
Anfängerpraktikum IV Zeeman

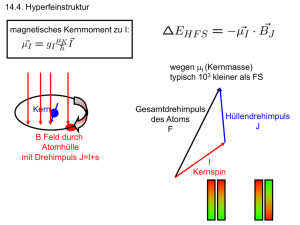
Anfängerpraktikum IV
Zeeman-Effekt, optisches Pumpen
Praktikumsbericht
René Sedlak, Simon Hönl
Tutor: Bernhard Herzog
Durchgeführt am 3.6./10.6.2013
Zeeman
Inhaltsverzeichnis
Inhaltsverzeichnis
1 Einleitung
4
2 Grundlagen
2.1 Quantenzahlen . . . . . . . . . . . . . . . . . . . . . . . . . .
2.1.1 Hauptquantenzahl n . . . . . . . . . . . . . . . . . . .
2.1.2 Bahndrehimpulsquantenzahl l . . . . . . . . . . . . . .
2.1.3 magnetische Quantenzahl ml . . . . . . . . . . . . . . .
2.1.4 Spinquantenzahl s . . . . . . . . . . . . . . . . . . . .
2.1.5 Drehimpuls-Quantenzahl j . . . . . . . . . . . . . . . .
2.2 Vektormodell . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3 Spin-Bahn-Kopplung . . . . . . . . . . . . . . . . . . . . . . .
2.3.1 Russel-Sanders-Kopplung . . . . . . . . . . . . . . . .
2.3.2 jj-Kopplung . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Magnetisches Moment des Elektrons und Wechselwirkung mit
schen Feldern . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5 Normaler Zeeman-Effekt . . . . . . . . . . . . . . . . . . . . .
2.5.1 Semiklassisches Modell . . . . . . . . . . . . . . . . . .
2.5.2 longitudinaler und transversaler Zeeman-Effekt . . . .
2.5.3 Richtungsquantelung . . . . . . . . . . . . . . . . . . .
2.6 anormaler Zeeman-Effekt . . . . . . . . . . . . . . . . . . . . .
2.6.1 Paschen-Back-Effekt . . . . . . . . . . . . . . . . . . .
2.7 Zeeman-Effekt der Feinstruktur . . . . . . . . . . . . . . . . .
2.8 Normaler Zeeman-Effekt an Cadnium . . . . . . . . . . . . . .
2.9 Zeeman-Effekt der Hyperfeinstruktur . . . . . . . . . . . . . .
2.10 Optisches Pumpen an Rubidium . . . . . . . . . . . . . . . . .
2.11 RF-Resonanzspektroskopie . . . . . . . . . . . . . . . . . . . .
2.12 Lummer-Gehrcke Platte . . . . . . . . . . . . . . . . . . . . .
4
4
4
4
4
5
5
5
6
6
6
3 Zeeman-Effekt: Aufbau und Durchführung
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
magneti. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
6
8
8
10
10
11
12
13
13
14
14
15
16
17
4 Zeeman-Effekt: Auswertung
18
4.1 Bestimmung der spezifischen Ladung . . . . . . . . . . . . . . . . . . . . 18
4.2 Polarisationseffekte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
5 Zeeman-Effekt: Fehlerbetrachtung
20
6 Optisches Pumpen: Aufbau und Durchführung
20
7 Optisches Pumpen: Auswertung
21
2
Zeeman
Inhaltsverzeichnis
8 Optisches Pumpen: Fehlerbetrachtung
23
9 Fazit
23
10 Anhang
23
10.1 Quellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3
Zeeman
1 Einleitung
1 Einleitung
Der Versuch soll den Praktikaten den Zeeman-Effekt und seine Anwendungen in der
Physik sowie grundlegende Messmethodiken vermitteln.
2 Grundlagen
Im folgenden sollen möglichst kurz die wichtigsten Grundlagen des Versuchs erläutert
werden.
2.1 Quantenzahlen
Der folgende Abschnitt ist mit einigen Ergänzungen übernommen aus unserem APBericht ”Quantenmodelle”
Das Elektron in einem Wasserstoffatom wird nach dem Bohr-Somerfeld -Modell charakterisiert durch seine Hauptquantenzahl n, seine Drehimpulsquantenzahl l, seine magnetische Quantenzahl ml und seine Spinquantenzahl s. Im Folgenden werden diese
Quantenzahlen und ihre Funktion näher erläutert:
2.1.1 Hauptquantenzahl n
n ∈ N beschreibt die Hauptquantenzahl des Elektrons. Sie beschreibt die Lage der Schale
des Elektrons im Atom und damit seine Lage im Coulomb-Potential. Je höher n, desto
höher ist die potentielle Energie des Zustands und desto größer ist der zeitlich gemittelte
Abstand des Elektrons vom Kern.
2.1.2 Bahndrehimpulsquantenzahl l
Diese Nebenquantenzahl kann Werte zwischen 0 ≤ l ≤ n − 1 annehmen und gibt an,
welchen mechanischen Drehimpuls das Elektron in seiner Bewegung bezüglich des Atomkerns hat. l charakterisiert außerdem das Orbital des Elektrons, wobei l = 0 das kugelsymmetrische sog. s-Orbital ist, l = 1 das p-Orbital etc.
In der Regel sind die Energieeigenwerte dieser Zustände entartet, d.h. es liegt die gleiche Energie für unterschiedliche l vor. In Mehrelektronensystemen wie beispielsweise bei
Alkalimetallen (Rb im Versuch) bzw. mehratomigen Systemen sowie der relativistischen
Quantenmechanik kann diese Entartung aufgehoben sein.
Für die Eigenwerte des Drehimpulsoperators L2 ergeben sich mit ~2 l(l + 1)
2.1.3 magnetische Quantenzahl ml
Diese Quantenzahl des Bahndrehimpulses nimmt diskrete Werte zwischen −l ≤ ml ≤ l,
also 2l + 1 verschiedene Werte an und charakterisiert den Beitrag des Drehimpulses in
4
Zeeman
2 Grundlagen
Richtung eines äußeren Magnetfeldes, also die Eigenwerte des Drehimpulsoperators in
z-Richtung Lz an. In der Regel sind auch Zustände verschiedener ml entartet, es sei
denn es liegt ein äußeres Magnetfeld an, den dann zu beobachtenden Effekt, bei dem
die Energieniveaus unter Einwirkung eines äußeren Magnetfeldes aufgespalten werden,
nennt man Zeeman-Effekt (s.u.).
2.1.4 Spinquantenzahl s
Diese Quantenzahl gibt in der Form ~2 s(s + 1) die Eigenwerte des Spinbetragsoperators
s2 . In diesem Fall kann s nur den Wert 12 annehmen. Nach dem Pauli-Prinzip muss sich
diese Zahl für zwei Elektronen auf dem selben Energieniveau unterscheiden. Dies wird
durch die magnetische Spinquantenzahl ms beschrieben, die die Orientierung des Spins
bezüglich der z-Achse angibt, sie kann den Wert − 12 und 12 annehmen.
Diese Überlegungen gelten nur für Einelektronensysteme wie das Wasserstoffatom gelten. Aufgrund der Tatsache, dass Alkalimetalle wie das Wasserstoffatom nur ein Valenzelektron besitzen, können sie unabhängig von der Kernladung auf ähnliche Weise wie
das Wasserstoffatom beschrieben werden, da die ”inneren” Elektronen das CoulombPotential des Kerns so ”abschirmen”, dass für das Valenzelektron ein ähnliches Potential
wie im Wasserstoffatom vorliegt.
2.1.5 Drehimpuls-Quantenzahl j
Berücksichtigt man die Spin-Bahn-Kopplung (s.u.), so beschreibt die Bahndrehimpulsquantenzahl l nicht mehr hinreichend das Verhalten des Elektrons, da l, m, und s nicht
mehr mit dem Hamilton-Operator H kommutieren. Daher muss l hier mit einer Quantenzahl j ersetzt werden, die den Gesamtdrehimpuls des Elektrons charakterisiert. Dabei
ist j = n − 12 mit n ∈ N
2.2 Vektormodell
Betrachtet man die Quantenzahlen j, l und s als Vektoren ~j, ~l und ~s, so ergibt sich ~j
als Gesamtdrehimpuls mit:
~j = ~l + ~s
(1)
p
mit |~j| = j(j + 1) · ~ (siehe Spin-Bahn-Kopplung).
Mit dem Kernspin I~ ergibt sich dann der Gesamtdrehimpuls F~ des Atoms durch:
F~ = I~ + ~j
Analoges gilt für die magnetischen Momente µj , µs , µl etc.
5
(2)
Zeeman
2 Grundlagen
2.3 Spin-Bahn-Kopplung
Die Spin-Bahn-Kopplung beschreibt die Wechselwirkung, welche zwischen dem Bahndrehimpuls und dem Spin verschiedener Teilchen stattfindet. Dies geschieht in MehrElektronensystemen und man unterscheidet hierbei zwischen der Russel-Sanders-Kopplung
(LS-Kopplung) und der jj-Kopplung. Bei den meisten Atomen tritt dabei eine Mischung
beider Kopplungsarten auf.
2.3.1 Russel-Sanders-Kopplung
Dieser Kopplungstyp ist eine Näherung und tritt auf, wenn die Kopplungsenergie h~l, ~si
gegenüber der Wechselwirkung der einzelnen Spins h~
si , s~j i und der Bahndrehimpulse
~
~
hli , lj i der Elektronen relativ klein ist.
Der Gesamtdrehimpuls J~ ergibt sich dann über die Summe der Bahndrehimpulse und
der Spins der Elektronen:
X
X
~l +
~ +S
~
~s = L
(3)
J~ =
~ 2 = J(J + 1) · ~2 . Dabei bestimmt L
~ den Gesamtbahndrehimpuls des Systems
wobei |J|
und damit dessen energetischen Zustand. Bei einer entgegengesetzten Änderung des
Bahndrehimpulses zweier Elektronen gilt damit ∆L = 0.
Die LS-Kopplung tritt vor allem bei leichten Atomen auf.
2.3.2 jj-Kopplung
Dieser Kopplungstyp tritt dann auf, wenn die Kopplungsenergie h~l, ~si gegenüber h~
si , s~j iund
h~li , l~j i relativ groß ist.
Der Gesamtdrehimpuls J~ ergibt sich dann durch:
X
~j
mit ~j = ~l + ~s
(4)
J~ =
Damit wird der energetische Zustand nicht mehr über einen Gesamtbahndrehimpuls
bestimmt.
Die jj -Kopplung tritt bei schweren Atomen auf.
2.4 Magnetisches Moment des Elektrons und Wechselwirkung mit
magnetischen Feldern
Wie oben bereits erwähnt, besitzt ein Elektron einen ”Eigendrehimpuls” (Spin) ~s, für
dessen Betrag gilt:
p
(5)
|~s| = s(s + 1) · ~
6
Zeeman
2 Grundlagen
Dabei existiert zu dem Spin ein magnetisches Moment µ~s für das gilt:
µ~s = −gs ·
e
~s
2m0
(6)
Wobei e die Elementarladung, m0 die Ruhemasse des Elektrons und gs = 2, 0023 der
Landé-Faktor (g-Faktor) des Elektrons sind.
Spin des Elektrons in Zusammenhang mit dem mag. Moment µs
(Quelle: Haken / Wolf - Atom- und Quantenphysik, Springer-Verlag, Stuttgart (2003)
Kreist ein Elektron um einen Atomkern, so erzeugt der fließende ”Strom” nach dem
Gesetz von Biot-Savart ein magnetisches Feld und dadurch ein weiteres magnetisches
:
Dipolmoment. Für dieses Moment µl gilt bei einem Strom I = − e·ω
2π
~
~ = − 1 ωr2 · e · A
µ~l = I · A
2
A
(7)
~ der Flächennormalvektor der umkreisten Fläche A ist. Mit dem Drehimpuls
Wobei A
~l = ~r × p~ ergibt sich:
µ~l = −
~l
1 e ~
· l = −gl µB
2 me
~
(8)
Wobei gl der g-Faktor des Bahndrehimpulses ist, also das Verhältnis zwischen dem magnetischen Moment und dem Gesamtdrehimpuls.
Mit dem Bohrschen Magneton µB = 2me e ~ = 9, 274078 · 10−24 Am2 gilt dann für das
magnetische Bahnmoment:
mu
~ l=
µB ~
·l
~
(9)
und für den Betrag |µ~l |:
|µ~l | = µB
p
l(l + 1) =
7
e p
~ l(l + 1)
2m
(10)
Zeeman
2 Grundlagen
2.5 Normaler Zeeman-Effekt
Der normale Zeeman Effekt bezieht sich auf einen Spezialfall des anormalen Zeeman
Effekts, bei dem lediglich der Bahnmagnetismus und nicht die Spin-Bahn-Kopplung
berücksichtigt wird. Daher tritt dieser auch nur bei Systemen auf, bei denen sich die
Spins der Elektronen gerade zu Null addieren, es sind also mindestens zwei Elektronen
notwendig.
2.5.1 Semiklassisches Modell
Diese Erklärung des normalen Zeeman-Effekts stammt von Zeeman und Lorentz und
ist noch vor der Zeit der Quantenmechanik entstanden. Sie basiert darauf, dass die
Abstrahlung einer elektromagnetischen Welle also Dipolstrahlung eines schwingenden
Elektrons zu verstehen ist. Dies entspricht in der klassischen Vorstellung dem Umlauf
eines Elektrons um den Atomkern. In der eindimensionalen Projektion dieser Oszillation
kann nun die Wechselwirkung mit dem äußeren Magnetfeld beschrieben werden. Dazu
werden die Komponenten des E-Felds nochmals zerlegt in drei Ersatzoszillationen, von
denen eine als linear polarisierte Felder parallel zum B-Feld und zwei zirkular polarisierte
Felder senkrecht zum B-Feld auftreten.
Zerlegung des E-Feldvektors in Ersatzoszillationen
(Quelle: Haken / Wolf - Atom- und Quantenphysik, Springer-Verlag, Stuttgart (2003)
Liegt kein äußeres Feld B~0 ans so Schwingen alle Ersatzoszillationen mit der ursprünglichen Frequenz des Elektrons ω0 . Liegt jedoch ein Feld an so wirkt auf die Ersatzoszillationen senkrecht zum Feld die Lorentzkraft:
~
F~L = −e · ~v × B
(11)
mit der Geschwindigkeit der Elektronen ~v .
Die parallele Ersatzoszillation ergibt also linear parallel zum B-Feld polarisiertes Licht,
während sich die Frequenz der Schwingung der Ersatzoszillationen 2 und 3 um den Betrag ∆ω = 12 · me0 · B0 = µ~B · B0 ändert. Abhängig von der Richtung der zirkularen
Oszillation werden die Ersatzelektronen dabei beschleunigt oder abgebremst.
Die Formel für ∆ω ergibt sich dabei über das Lösen der Bewegungsgleichung für das
8
Zeeman
2 Grundlagen
Elektron. Es kann hierfür zunächst für die Ersatzelektronen die im Atom wirkende Coulombkraft mit der Zentrifugalkraft gleichgesetzt werden, so dass gilt:
mω02~r =
Ze2
· ~r
4π0 r3
(12)
Zusätzlich wirkt auf die Ersatzelektronen 2 und 3 noch die Lorentzkraft, so dass folgende
Differenzialgleichungen vervollständigt werden:
mẍ + mω02 x − eẏB0 = 0
mÿ + mω02 y − eẋB0 = 0
mz̈ + mω02 z = 0
(13)
(14)
(15)
Da auf die z-Komponente keine Lorentzkraft wirkt, können wir die Lösung für diese
Gleichung sofort als eine Oszillation mit der Frequenz ω0 angeben mit:
z = z0 · eiω0 t
(16)
(10) und (11) lassen sich nun mit den Substitutionen u = x+iy und v = x−iy entkoppeln
und separat schreiben:
mü + mω02 u + ieB0 u̇ = 0
mv̈ + mω02 v − ieB0 v̇ = 0
(17)
(18)
Die Fundamentalsysteme ergeben sich mit:
r
i
F S(u) : e
(
r
i
F S(v) : e
eB0
2m
)
0
( eB
2m )
2
2
0
Für große ω0 >> eB
kann der Term
2m
Fundamentalsysteme ergeben:
!
eB
+ω02 − 2m0
r
·t
i −
, e
!
+ω02 +
e2 B02
4m2
eB0
2m
(
r
·t
i −
, e
eB0
2m
2
)
2
0
( eB
2m )
!
eB
+ω02 − 2m0
·t
(19)
!
+ω02 +
eB0
2m
·t
(20)
(21)
vernachlässigt werden, wodurch sich folgende
eB0
2 eB0
F S(u) : ei(ω0 − 2m )·t , ei(−ω0 − 2m )·t
eB0
eB0
F S(v) : ei(ω0 + 2m )·t , ei(ω0 + 2m )·t
(22)
(23)
(24)
Definiere nun:
eB0
2m
eB
0
ω + = ω0 +
2m
ω − = ω0 −
(25)
(26)
(27)
9
Zeeman
2 Grundlagen
Man erkennt, dass ω − bzw. ω + die Frequenzen der links- bzw. rechtsdrehenden Ersatzoszillationen 2 und 3 sind.
Es gilt also:
µB
eB0
=
· B0
2m
~
1 eB0
µB
∆ν =
=
· B0
4π m
h
∆ω =
(28)
(29)
Solange das Magnetfeld anliegt, absorbieren und emittieren die Ersatzelektronen mit
dieser verschobenen Frequenz, wodurch sich für die Ersatzelektronen 1, 2 und 3 neue
Spektrallinien ergeben.
Ersatzelektron 1 strahlt dabei mit der Charakteristik eines Hertzschen Dipols, es wird
also keine Strahlung in Richtung der Dipolachse abgegeben. Dieser Anteil des Spektrums
wird π-Strahlung genannt. Ersatzelektron 2 und 3 Strahlen zirkular polarisiertes Licht
ab, wobei durch die Überlagerung beider Wellen ein senkrecht dazu linear polarisierter
Teil auftritt. Diese Komponenten heißen σ + und σ − . Das σ + Licht ist dabei links-zirkular
polarisiert relativ zu den Kraftlinien des B0 Feldes. Dieser Unterschied in der Polarisation
wird beim optischen Pumpen zum selektiven Bevölkern einzelner Niveaus und damit zur
Erzeugung einer Spin-Orientierung genutzt.
2.5.2 longitudinaler und transversaler Zeeman-Effekt
Abhängig von der Sicht auf die B-Feldlinien unterscheidet man zwischen dem longitudinalen Zeeman-Effekt, bei dem man parallel auf die Feldlinien sieht und somit durch
die Sicht entlang der Dipolachse von 3 nur die σ Spektrallinien sehen kann und dem
transversalen Zeeman-Effekt, bei dem man senkrecht auf die Feldlinien sieht und so
die π-Linie als parallel zu den Feldlinien linear polarisiertes Licht und die σ-Linien als
senkrecht zu den Feldlinien linear polarisiertes Licht wahrnimmt.
2.5.3 Richtungsquantelung
Diskrete Spinorientierung mit Vorzugsrichtung entlang des z-Achse
10
Zeeman
2 Grundlagen
(Quelle: Haken / Wolf - Atom- und Quantenphysik, Springer-Verlag, Stuttgart (2003)
In obiger Abbildung ist die Orientierung des Spins in einem äußeren Magnetfeld B0
zu sehen, wobei sich der Spin entlang der z-Achse parallel oder antiparallel orientieren
kann. Dabei ergibt sich für den Spin in z-Richtung:
sz = ms ~
(30)
mit der magnetischen Quantenzahl ms des Spins.
Für das magnetische Moment entlang der z-Achse gilt dann:
µs,z = −gs ms µB
µs,z ≈ ±1, 00116µB
(31)
(32)
Es gibt also eine Präzession des magnetischen Moments und des Spins in der xy-Ebene.
2.6 anormaler Zeeman-Effekt
Beim anormalen Zeeman-Effekt addieren sich die Spins nicht zu null, was in den meisten
Atomen der Fall ist, weshalb es durch die Überlagerung des Bahndrehimpulses l und des
Spins s zu einem veränderten optischen Übergang kommt.
Die g-Faktoren der beteiligten Terme unterscheiden sich, da die Terme unterschiedliche
Anteile des Spins und des Bahnmagnetismus enthalten. Mit dem Gesamtdrehimpuls j
werden sie daher mit gj bezeichnet. Der Landé-Faktor gj ergibt sich dabei durch:
gj = 1 +
j(j + 1) + s(2 + 1) − l(l + 1)
2 · j(j + 1)
(33)
Da die Aufspaltung der Spektrallinien im Grundzustand und im angeregten Zustand
unterschiedlich groß sind, kommt es zu einer größeren Anzahl von Spektrallinien.
Aufspaltung der D1 - und D2 -Linie in Natrium bei einer Flussdichte von B = 3T
(Quelle: Haken / Wolf - Atom- und Quantenphysik, Springer-Verlag, Stuttgart (2003)
11
Zeeman
2 Grundlagen
Wie oben zu sehen ist, wird beim Anlegen eines B-Feldes die D1 Linie in vier Komponenten aufgespalten, während die D2 Linie in sechs Komponenten aufgespalten wird.
Dies liegt daran, dass im Natriumatom drei Terme vorliegen, von denen aus energetische
Übergänge möglich sind, 2 S1,2 , 2 P1,2 und 2 P3,2 .
Für die magnetischen Momente in z-Richtung gilt dabei (s.o.):
(~µj )j,z = −mj gj µB
(34)
So dass die magnetische Zusatzenergie Vmj = (~µj )j,z · B0 aufgewendet werden muss.
Dabei ist die Anzahl der Spektrallinien durch mj gegeben und beträgt 2j + 1. Dabei
sind die Linien nun nicht mehr äquidistant, sondern der Energieunterschied zwischen
den Niveaus beträgt
∆Emj ,mj−1 = gj · µB · B0
(35)
und hängt also von l, j und s ab.
Die g-Faktoren sind hier gegeben für 2 S1,2 mit gj = 2, für 2 P1,2 mit gj = 32 und für 2 P3,2
mit gj = 34 . Wie diese Faktoren zustande kommen wird im folgenden geklärt.
Es sei zunächst gegeben, dass für optische Übergänge die Auswahlregeln ∆mj = 0 für
π Übergänge und ∆mj = ±1 für σ-Übergänge gelten. Es ergeben sich insgesamt zehn
verschiedene Übergänge, nämlich vier Übergänge zwischen 2 S1,2 und 2 P1,2 in der D1 -Linie
und sechs Übergänge zwischen 2 S1,2 und 2 P3,2 in der D2 -Linie.
Aufspaltung der D1 bzw. D2 Linie von Natrium
2.6.1 Paschen-Back-Effekt
Liegt ein hinreichend starkes Magnetfeld an dem beobachteten Stoff an, so ist die SpinBahn-Kopplung im Vergleich dazu sehr schwach, so dass sie vernachlässigt werden kann.
12
Zeeman
2 Grundlagen
Das magnetische Moment ist dann gegeben durch:
X
X
µz = 1 · µB ·
(ml )i + 2 · µB ·
(ms )i
i
(36)
i
2.7 Zeeman-Effekt der Feinstruktur
Die oben genannten Effekte der Spin-Bahn-Kopplung führen im Atom zu einer Aufspaltung der Energieniveaus entsprechend der Ausrichtung von Spin und Bahndrehimpuls,
man spricht von einer Dublett- bzw. Multiplett-Struktur oder Feinstruktur der Sprektrallinien. Für das im Versuch verwendete Rubidium liegt der angeregte Zustand nicht
in einer höheren Schale, sondern in einem anderen Orbital.
Die Energieterme unterscheiden sich also abhängig davon, ob die magnetischen Momente
parallel oder antiparallel zueinander stehen. Da wir in unserem Fall ein Einelektronensystem behandeln gilt s = 21 und damit gilt für den Gesamtdrehimpuls j = |l ± s| = |l ± 21 |.
p
Es gilt hier wieder |~j| = j · (j + 1) · ~. Es ergeben sich also bei l 6= 0 immer zwei
Zustände mit unterschiedlichen Gesamtdrehimpulsen. Ist l = 0, so ist j = 12 und es gibt
keine Aufspaltung, man spricht von einem Singulett-Zustand.
2.8 Normaler Zeeman-Effekt an Cadnium
Bei Cadnium ist die oberste Schale als s-Orbital mit zwei Elektronen besetzt, das heißt,
die Spins addieren sich zu Null. Dabei werden die inneren 46 Elektronen vernachlässigt,
da sie sich in voll besetzten Orbitalen befinden und dadurch der gesamte Bahndrehimpuls
der gesamte Spin sich zu Null addieren und daher keinen Beitrag zu den beobachteten
Effekten liefern.
Da die beiden Elektronen im obersten s-Orbital nach dem Pauli-Prinzip einen entgegengesetzten Spin haben müssen, gilt außerdem J = L und Jz = M . Man erwartet also den
normalen Zeeman-Effekt.
13
Zeeman
2 Grundlagen
Aufspaltung der Energieniveaus in Cadnium
(Quelle: Haken / Wolf - Atom- und Quantenphysik, Springer-Verlag, Stuttgart (2003)
Mit µB = 9, 27401 · 10−24 Am2 folgt für m = 1 pro Tesla im angelegten Magnetfeld:
∆E = 5, 788 · 10−5 eV
(37)
Der Nachweis des Spektrums ist trotz des geringen Energieunterschieds möglich, weil
man mit Hilfe der Lummer-Gehrcke-Platte sehr genau zwischen leicht unterschiedlichen Wellenlängen differenzieren kann und bei einem hinreichend starken Magnetfeld
die Aufspaltung der Linien als eine Vervielfältigung der ursprünglichen Spektrallinien
beobachten kann.
2.9 Zeeman-Effekt der Hyperfeinstruktur
Wie in der Feinstruktur der Spin des Elektrons an den Bahndrehimpuls koppeln kann,
so kann auch der Kernspin I schwach an den Bahndrehimpuls koppeln, so dass nun der
Gesamtdrehimpuls F = J ± I betrachtet werden muss. Die Folge ist eine weitere Aufspaltung der Energieniveaus. Die Kopplung wird über den Landé-Faktor gF beschrieben
für den gilt:
gF = gJ ·
F (F + 1) + J(J + 1) − I(I + 1)
2F (F + 1)
(38)
Es ergibt sich wieder eine energetische Aufspaltung für −F ≤ mF ≤ F und somit 2F + 1
unterschiedliche Niveaus.
2.10 Optisches Pumpen an Rubidium
Beim optischen Pumpen wird der Zeeman-Effekt ausgenutzt. Die Energieniveaus des
Valenzelektrons spalten sich beim Anlegen eines äußeren Magnetfeldes auf in (s.o.) zirkular polarisierte und linear polarisierte Anteile. Wird das Valenzelektron nun durch ein
zirkular polarisiertes Photon angeregt, so kann ein optischer Übergang nur dann stattfinden, wenn sich der Drehimpuls in z-Richtung im ~ erhöht. Diese Forderung nennt man
Auswahlregel (s.u.), sie folgt aus der Drehimpulserhaltung.
Dadurch, dass nur höherenergetische Zustände angenommen werden können, kommt es
nach kurzer Zeit zu einer Überbevölkerung im Grundzustand bei m = 2, es können also
keine Photonen mehr absorbiert werden, da das Elektron nicht die Möglichkeit hat, seinen Drehimpuls zu erhöhen, man spricht dann von einer Besetzungsinversion; tritt diese
ein, so liegt ein Maximum in der Intensität des transmittierten Lichts vor.
Im Versuch wird Rubidium, welches als Alkalimetall nur ein Valenzelektron besitzt, gepumpt. Für dieses ergeben sich folgende Energieniveaus:
14
Zeeman
2 Grundlagen
Energieniveaus von Rubidium mit erlaubten Übergängen bei longitudinal eingestrahlten
zirkular polarisiertem Licht
(Quelle: Teachspin; optical pumping of rubidium OP1-A; Buffalo 2002
2.11 RF-Resonanzspektroskopie
Bei der RF-Spektroskopie nutzt man ein schnell oszillierendes Magnetfeld, um über die
magnetischen Übergänge die Zeeman-Aufspaltung eines Atoms zu messen. Da man hier
magnetische Übergänge betrachtet, gilt hier auch nicht die Einschränkung der Übergänge
durch die Auswahlregeln für optische Übergänge.
Durch das oszillierende Magnetfeld können zwar nur Übergänge mit geringer Energieänderung E = hν betrachtet werden, diese aber sehr präzise.
Dieser Umstand ist für die Beobachtung des Pumpprozesses sehr wichtig, denn um eine Besetzungsinversion zu erzeugen, muss die Frequenz sehr präzise eingestellt werden,
da einige Elektronen sonst wieder auf ihren Grundzustand zurückfallen und somit wieder Photonen absorbieren können. Die Besetzungsinversion zeigt sich dadurch, dass das
Licht nicht mehr absorbiert wird und somit an der Photodiode ein Intensitätsmaximum
auftritt.
Die Energieaufspaltung V lässt sich nun wieder schreiben als:
−gF µB mF B
(39)
und damit die Energiedifferenz zwischen zwei Zuständen ∆V als:
∆V = −gF µB (mF − (mF + 1))B
= gF µB B
15
(40)
(41)
Zeeman
2 Grundlagen
Es gilt also mit der Energie des oszillierenden Magnetfeldes h · ν
hν = gF µB B
hν
⇒ gF =
µB B
(42)
(43)
2.12 Lummer-Gehrcke Platte
Aufbau der Lummer-Gehrcke-Platte
(Quelle: Leybold; Handblätter Physik; P 6.2.7.1
Wie oben zu sehen ist, besteht die Platte aus einem Prisma, das zur Einkopplung des
Strahls dient, und einer transparenten Platte, an dessen Grenzflächen der Lichtstrahl
transmittiert bzw. reflektiert werden. Die Strahlen treffen dabei in einem Winkel auf die
Oberfläche, der nur wenig größer ist als der Winkel der Totalreflexion, so dass bei jedem
Reflex nur ein kleiner Teil des Lichtstrahls ausgekoppelt wird.
Die transmittierten Strahlen interferieren ähnlich wie beim optischen Gitter miteinander,
so dass sich hinter der Linse Hauptmaxima abzeichnen.
Für den Winkel αk des k-ten Maximums gilt:
p
(44)
2d · n2 − sin2 αk = k · λ
Dabei ist n der Brechungsindex der Platte, d die Dicke und λ die Wellenlänge.
16
Zeeman
3 Zeeman-Effekt: Aufbau und Durchführung
3 Zeeman-Effekt: Aufbau und Durchführung
Aufbau zur Messung des Zeeman-Effekts
(Quelle: Leybold; Handblätter Physik; P 6.2.7.1
Der Aufbau besteht aus einer Cd-Dampflampe, die als Lichtquelle dient, einem Elektromagneten, der die Cd-Lampe mit einem homogenen Magnetfeld durchsetzt, einem
Rotfilter, der aus dem Spektrum der Dampflampe das rote Licht mit einer Wellenlänge
von λ = 643, 8nm filtert. Dahinter befindet sich die Lummer-Gehrcke Platte, hinter der
durch ein Fernrohr die Spektrallinien betrachtet werden können.
Zwischen Lummer-Gehrcke Platte und Fernrohr kann außerdem ein λ4 -Plättchen bzw.
ein Filter für linear polarisiertes Licht angebracht werden, so dass die Polarisationsrichtung des Lichts bestimmt werden kann.
Der Strom durch die Polschuhe des Elektromagneten kann geregelt und über eine Hallsonde gemessen werden, außerdem können die Polschuhe gedreht werden, so dass longitudinale und transversale Betrachtungen möglich sind.
Für die Messung wird zunächst die Cd-Lampe aufgeheizt und das Fernrohr so justiert,
dass im Sichtfeld das Licht der Lampe zu sehen ist. Danach wird der Elektromagnet
eingeschaltet und die Stromstärke so eingestellt, dass die Spektrallinien einen konstanten Abstand zueinander aufweisen. Mit der Hallsonde wird die Flussdichte zwischen den
Polschuhen bestimmt und der Vorgang fünf mal wiederholt.
Anschließend wird qualitativ die Polarisation der zu sehenden Linien mit Hilfe der Polarisationsfilter bestimmt. Der gesamte Vorgang wird einmal für die Betrachtung des
longitudinalen und des transversalen Zeeman-Effekts wiederholt.
17
Zeeman
4 Zeeman-Effekt: Auswertung
4 Zeeman-Effekt: Auswertung
4.1 Bestimmung der spezifischen Ladung
Für die Linie mit m = 1 gilt in Cadnium:
e
·~·B
2me
e
2∆E
⇔
=
me
~B
(45)
∆E =
(46)
Für zwei Photonen gilt dann:
e
2h(ν0 − ν1 )
4π(ν0 − ν1 )
=
=
me
~B
B
mit ν1 > ν0
(47)
Für den Fehler gilt dann, da hier nur B mit einem Fehler behaftet ist:
δ mee
e
me
=
δB
B
(48)
Durch die äquidistante Einstellung der Linien sieht man nun zwischen dem k-ten und
dem k + 1-ten Maximum bei k + 13 die aufgespaltene Linie. Es gilt also:
1
· λ0
(49)
k · λ1 = k +
3
1
⇔ λ1 = 1 +
· λ0
(50)
3k
Aus (44) folgt mit α ≈ 90◦ :
√
k · λ = 2d n2 − 1
2d √ 2
k=
n −1
λ
(51)
(52)
Mit lambda0 = 643, 8nm (Interferenzfilter), d = 4, 04mm und n = 1, 4567 gilt dann:
k=
2 · 4, 04mm p
· 1, 45672 − 1 = 13294
643, 8nm
(53)
Damit folgt für λ1 :
λ1 = 1 +
1
3 · 13294
· 643, 8nm = 643, 816nm
18
(54)
Zeeman
4 Zeeman-Effekt: Auswertung
Es gilt:
c
λ
14
⇒ ν0 = 4, 65661 · 10 Hz
ν1 = 4, 65649 · 1014 Hz
c=λ·ν ⇔ν =
(55)
(56)
(57)
Für die longitudinale Betrachtung beträgt der Abstand zwischen dem Maximum k-ter
Ordnung und der Aufspaltungslinie
1
λ1 = 1 +
λ0 ⇒ ν1 = 4, 65652 · 1014 Hz
(58)
4
Unten sind die Versuchsergenisse tabellarisch dargestellt.
Messergebnisse für der transversalen Beobachtung
Messergebnisse für der longitudinalen Beobachtung
P10 e e
1
C
Damit ergibt sich der Mittelwert me = 10 i=1 me = 1, 8592 · 1011 kg
i
4.2 Polarisationseffekte
Wie zu erwarten war, sieht man bei der transversalen Beobachtung nach Anbringen
eines Polarisationsfilters im Strahlengang zwischen der Lummer-Gehrcke-Platte und dem
Fernrohr, dass die zu sehenden Linien linear polarisiert sind, wobei die mittlere Linie
senkrecht zu den beiden äußeren polarisiert ist.
Bei der longitudinalen Betrachtung stellt man nach Ergänzen des Filters mit einem
19
Zeeman
5 Zeeman-Effekt: Fehlerbetrachtung
λ/4-Plättchen, welches das zirkular polarisierte Licht wieder linear polarisiert, fest, dass
die beiden noch zu sehenden Linien mit jeweils entgegengesetztem Drehsinn zirkular
zueinander polarisiert sind (die Linien lassen sich durch Drehen des Polarisationsfilters
abwechselnd ausblenden); auch dies stimmt mit den Erwartungen überein.
5 Zeeman-Effekt: Fehlerbetrachtung
Trotz der immensen Fehler, die sich durch die große Abschätzung des Fehlers bei der
Messung von B ergeben haben, sind unsere Versuchsergebnisse im Vergleich zum LiC
mit einer Abweichung von 5, 7% ein sehr brauchbares
teraturwert mee = 1, 759 · 1011 kg
Ergebnis. Das Ergebnis könnte noch verbessert werden, wenn eine größere Anzahl an
Messreihen durchgeführt würde und der Fehler bei der Messung des B-Feldes minimiert
werden könnte.
6 Optisches Pumpen: Aufbau und Durchführung
In diesem Versuch soll mit Ausnutzung des Zeeman-Effekts die Energiedifferenz der
Hyperfeinaufspaltung von 85 Rb und 87 Rb über ein statisches Magnetfeld ausgemessen
werden. Mit Hilfe des Landé-Faktors gF kann dann mit J und S der Kernspin I ermittelt
werden. gj ist dabei bekannt mit gj = 2.
Aufbau zum Versuch ”Optisches Pumpen”
(Quelle: Runge, Bernd-Uwe: Skript zu AP (2012)
Der Aufbau besteht dabei aus einer temperaturstabilisierten Rubidiumzelle, die von
einem hochfrequenten Sweep-Feld durchsetzt wird, dessen Frequenz sich in sechs Stufen
regeln lässt, zusätzlich lässt sich für höhere Frequenzen noch ein Offset-Feld zuschalten.
Die Signale werden mit einer Photodiode an ein Oszilloskop übertragen.
20
Zeeman
7 Optisches Pumpen: Auswertung
7 Optisches Pumpen: Auswertung
Für das B-Feld der Sweep-Spule gilt mit der Windungszahl n = 80 und der mittleren
Spulendicke R = 0, 09m (siehe Versuchsbeschreibung):
µT
8 µ0 · 80 · I
≈ I · 799, 268
B=√
A
125 0, 09m
(59)
Mit der Energie der Anregungsfrequenz E = h · ν ergeben sich folgende Werte für E in
Abhängigkeit der Flussdichte B:
Versuchsergebnisse des Versuchs ”Optisches Pumpen”
lineare Regression der Versuchsergebnisse des Versuchs ”Optisches Pumpen”
Diese Versuchsergebnisse entsprechen nicht den Erwartungen und sind vermutlich auf
einen systematischen Fehler in der Messung zurückzuführen, wir werden die Versuchsergebnisse im folgenden trotzdem weiter verwenden und exemplarisch die Auswertung
durchführen.
21
Zeeman
7 Optisches Pumpen: Auswertung
Durch eine lineare Regression ergibt sich für das B-Feld:
T
· E + 70µT
meV
T
· E + 80µT
BB = (35, 2 ± 0, 05)
meV
BA = (29, 2 ± 0, 05)
(60)
(61)
Es gilt also für die Landé-Faktoren:
E
µB · B
1
·E
B=
µB gF
gF =
(62)
(63)
1
2
≈ 0, 59 =
ˆ
T
3
µB · (29, 2 ± 0, 05) meV
1
1
=
≈ 0, 49 =
ˆ
T
2
µB · (35, 2 ± 0, 05) meV
⇒ gFA =
(64)
gFB
(65)
(66)
Für das Pumpniveau gilt dabei S = 12 , L = 0, J = L + S =
gJ = 1 +
1 1
(
2 2
Mit der Formel
gF = gJ ·
1
2
und damit folgt
+ 1) + 12 ( 12 + 1) − 0(0 − 1)
=2
2 · 12 ( 12 + 1)
F (F + 1) + J(J + 1) − I(I + 1)
2F (F + 1)
(67)
(68)
Ersetzt man nun F mit F = I + J, so folgt
gF = 2 ·
(J + I)((J + I) + 1) + J(J + 1) − I(I + 1)
2(J + I)((J + I) + 1)
(69)
und damit folgt für das gemessene Isotop A ein Kernspin von I = 1 und für Isotop B
ein Kernspin von I = 23 .
Isotop B müsste demnach 87 Rb sein, jedoch kann der Wert für I von Isotop A keinem
erwarteten Stoff zugeornet werden. Wie oben bereits erwähnt, liegt dies jedoch an den
stark fehlerbehafteten Messwerten.
22
Zeeman
8 Optisches Pumpen: Fehlerbetrachtung
8 Optisches Pumpen: Fehlerbetrachtung
Grundsätzlich ermöglicht der Aufbau von Leybold-Heraeus keine so präzisen Messungen
wie der Aufbau von Teachspin, bei dem nach längerer Kalibrierung präzise Messungen
möglich sein sollten, leider war dieser Aufbau am Versuchstag jedoch defekt.
Eine große Fehlerquelle bei dem verwendeten Aufbau ist die Eigenschaft, dass viele
Parameter bereits voreingestellt sind und während der Messung nicht weiter kalibriert
werden können.
Der Aufbau birgt viele weitere Fehlerquellen, wie beispielsweise die Rb-Zelle oder die
Messapparatur.
9 Fazit
Der Versuch zum Zeeman-Effekt hat überraschend präzise Ergebnisse geliefert angesichts
der Tatsache, dass hier die Äquidistanz der Linien per Augenmaß bestimmt werden
musste. Der Versuch zum optischen Pumpen hat leider keine verwertbaren Ergebnisse
geliefert, was vermutlich auf einen Fehler beim Messvorgang oder auf einen Defekt der
Messapparatur zurückzuführen ist. Allgemein ist das zugrunde liegende physikalische
Prinzip des Zeemann-Effekts und die Messmethodik jedoch klar geworden und hat bei
den Autoren zu einem tieferen Verständnis der Thematik geführt.
10 Anhang
10.1 Quellen
• Haken / Wolf - Atom- und Quantenphysik, Springer-Verlag, Stuttgart (2003)
• Runge, Bernd-Uwe: Skript zum AP (2012)
• Riegger, Luis; Dehm, Udo: Praktikumsbericht ”Zeeman-Effekt und optisches Pumpen” (2010)
• Rommel, Michael; Putnik, Martin: Praktikumsbericht ”Zeeman-Effekt und optisches Pumpen” (2010)
• Mahlbacher, Markus; Möller, Thomas: Praktikumsbericht ”Zeeman-Effekt und optisches Pumpen” (2012)
• Teachspin; optical pumping of rubidium OP1-A; Buffalo 2002
• Leybold; Handblätter Physik
23