Lecture 18

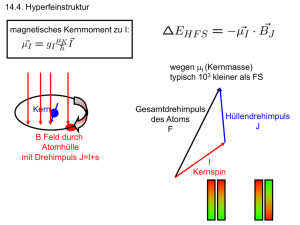
Normaler Zeeman Effekt
Normaler Zeeman Effekt
164
R. G
Normaler
Zeeman Effekt
Kapitel 4: Das Wasserstoffatom
ROSS
ν
B=0
Δm = -1
Δν
ν0
Δν
E B
l=2
Δm = 0
E || B
Δm = +1
m B=0
B>0
m
+2
+2
+1
+1
0
l=2
0
-1
-1
-2
-2
E B
transversale Beobachtung
linear polarisiert
longitudinale Beobachtung
zirkular polarisiert
(a)
B>0
Δm = +1 0 -1
B
l=1
Δm = -1 0 +1
+1
0
l=1
0
-1
-1
Absorption
+1
Emission
(b)
Abbildung 4.14: Normaler Zeeman-Effekt: (a) Aufspaltungsbild und Polarisation einer Spektrallinie mit
der Mittenfrequenz n0 bei transversaler und longitudinaler Beobachtungsrichtung. (b) Termschema für
¨
Zeeman Effekt des Kerns
Muskel dunkel
Muskel hell
Magnetisches Moment in der Quantenmechanik
z
Spin (Drehimpuls) is quantisiert
Spin hat im Magnetfeld nur feste
Einstellmöglichkeiten
einzelnes Proton
Ein Spin 1/2 Teilchen hat nur zwei
Einstellmöglichkeiten im äußeren magnetischen Feld
Präzession eines magnetischen Moments
z
Drehmoment
Präzession
Larmor Frequenz
Spins präzidieren aufgrund des Drehmomentes und
des Drehimpulses
Energie eines magnetischen Moments im B-Feld
z
Energie
Magnetisierung
Quermagnetisierung (quer zu B)
6.7.1019 Protonen
y
z
x
Längsmagnetisierung (längs zu B)
z
y
x
Längsmagnetisierung
z
6.7.1019 Protonen
Boltzmann-Gesetz
6.7 ppm
Überschuss-Spins
Spin-Anregungen
Radiofrequenz kann Übergänge zwischen Spinzuständen erzeugen
z
z
y
x
M
x
Radiofrequenz
RF Feld
Rabifrequenz
y
Anomaler Zeeman Effekt
4.7. anomalous Zeeman effect
LS coupling in an external magnetic field
assume that the magnetic field is weak compared to that
of the orbiting electron
spin orbit coupling is conserved in weak fields
Anomaler Zeeman Effekt
4.7. anomalous Zeeman effect
note: magnetic moment and j
are not anymore parallel
Anomaler Zeeman Effekt
Abschnitt 4.7
(a)
z,B
169
P HYSIK IV
z,B
(c)
J
J
J
Jz
z
L
S
(b)
L
S
z,B
L
µs
µj
µl
J
µs
S
µl
µj
<µj>z
<µj>
<µj>
<µj>z
Abbildung 4.15: (a) Präzession von J um die z-Achse in einem äußeren Magnetfeld. (b) Vektorielle Zusammensetzung des Drehimpulses und des von ihm erzeugten magnetischen Moments. (c) Präzession
aller magnetischen Momente und Drehimpulse um die Magnetfeldrichtung.
Anomaler Zeeman Effekt
4.7. anomalous Zeeman effect
time average
< µj >=
µj · j
|j|
=
< µj >=
e
2me
gj
l·j
|j|
+ gs
s·j
|j|
j(j + 1)µB
Landé factor for j
gj = 1 +
j(j + 1) + s(s + 1)
2j(j + 1)
l(l + 1)
the splitting now depends on j and l
⇥
Anomaler Zeeman Effekt
4.7. anomalous Zeeman effect
examples for different j
this is the case for sodium
Paschen Back Effekt
4.7. anomalous Zeeman effect
Paschen Back effect
• strong magnetic fields
• l and s precess independently around B
ml =
ms =
µz =
B
l
l... + l
1/2 . . . + 1/2
µB (ml + 2ms )
Eml ,ms = µB B(ml + 2ms )
2p1/2 , 2p3/2
s
2s1/2
0
-1
1/2
1/2
-1/2
1/2
-1/2
-1/2
0
1/2
0
-1/2
1
0
-1,1
selection rules
ms = 0
ml = ±1, 0
174
Paschen Back Effekt
(a)
schwaches Feld
R. G ROSS
mj
Kapitel 4: Das Wasserstoffatom
starkes Feld
(b)
+ 3/2
+½
3p3/2
- ½ +1/3 ΔE
3p
FS
- 3/2
−2/3 ΔEFS
3p1/2
+½
-½
+½
3s1/2
ms m
½
1
½
0
½
-½
-1
1
-½
0
-½
-1
½
0
-½
0
3s
-½
σπ πσ
σ π σ
σ
π
σ
Abbildung 4.18: Paschen-Back-Effekt beim Natriumatom: (a) Situation bei schwachem Magnetfeld: An-
omaler Zeeman-Effekt. (b) Niveauaufspaltung im starken Magnetfeld: Paschen-Back-Effekt. Zum Vergleich ist die Feinstrukturaufspaltung (vergrößert) gezeigt.
Vollständiges Termschema des H-Atoms
Abschnitt 4.9
P HYSIK IV
f
E
n=4
3d5/2
n=3
3p3/2
3d3/2
3s1/2 ,3p1/2
3d5/2
3p3/2
3d3/2
3s1/2 ,3p1/2
3
2
2
1
2
1
1
0
1
0
2
1
n=2
2p3/2
2p3/2
2s1/2
2s1/2 ,2p1/2
2p1/2
0
1
1s1/2
0
1
0
n=1
1s1/2
Bohrsche
Energieniveaus
Schrödinger-Gl.
ohne Spin
Feinstruktur
nach Dirac
LS-Kopplung
+ rel. Massenzunahme
LambVerschiebung
Strahlungskorrektur (QED)
1
HyperFeinstruktur
Kerneffekte
Abbildung 4.19: Vollständiges Termschema des Wasserstoffatoms mit allen bisher bekannten Wechsel-
wirkungen. Die Fein- und Hyperfeinstruktur, sowie die Lamb-Shift sind aus Gründen der Übersichtlichkeit
nicht maßstabsgerecht gezeichnet.
177
die
wei
ahten
geng
tehe
eiger
dusen
ein
agnge
en
ch
J
(linearer Stark-Effekt, Abb. 10.31).
ben, also auch im elektrischen Feld entartet bleiben.
Die Stark-Verschiebung ist im 32 S1/2 -Grundzustand
Auch ohne permanentes elektrisches Dipolmoment
2
kleiner
als
in
den
angeregten
3
P-Zuständen, sowird im elektrischen Feld durch die entgegengesetzte
dass die Stark-Komponenten der Linien zu kleineren
Verschiebung der positiven bzw. negativen Ladungen
Frequenzen hin verschoben werden.
(dielektrische Polarisation, siehe Bd. 2, Abschn. Aus
1.7 der Messung der Aufspaltung und Verschieund 1.8) ein induziertes elektrisches Dipolmoment
bung lässt sich gemäß (10.52) die Polarisierbarkeit
Stark Effekt
pind
el
α̃ bestimmen. Sie ist, wie in Abschn. 9.4.3 gezeigt
= α̃ · E
(10.51)
erzeugt. Die Polarisierbarkeit α̃, welche ein Maß für
E die
32 P3 / 2
Verschiebbarkeit der Ladungen im elektrischen Feld
± 3 / 2 −60
±1 / 2
2
3 P1/ 2
a)
< pel >
H
b)
→
O
→
→
J
32 S1/ 2
J
Mh
β
→
p el
∆E = − < p el
→
> ⋅M⋅|E|
Abb. 10.31a,b. Zum linearen Stark-Effekt
a)
1
−20
3
νb
νa
< pel >
H
12 3
1
2
±1 / 2 −40
νa νb
E
∆ ν− /10 − 3 cm−1
MJ
23
ν
1 2
E2 / 1014 V 2m−2
b)
Abb. 10.32a,b. Verschiebung und Aufspaltung der Terme
im Na-Atom auf Grund des quadratischen Stark-Effektes.
(a) Termschema; (b) Abhängigkeit der Wellenzahlen der
Na-D-Linien von E2 [10.16]
lich
die
bita
Mo
sch
und
gew
10.
Bei
ein
pul
Ele
Bd.
lek
kan
che
von
(Fr
hoh
Do