A 1 Zeeman-Effekt und Fabry-Pérot-Interferometer

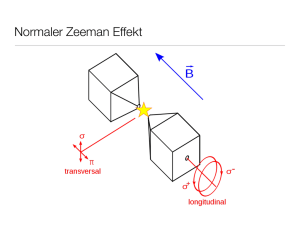
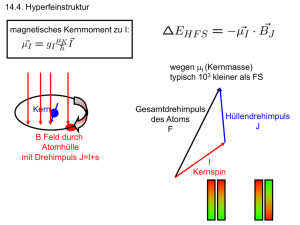
Universität Potsdam Institut für Physik und Astronomie Physikalisches Praktikum für Fortgeschrittene 2012 A 1 Zeeman‐Effekt und Fabry‐Pérot‐Interferometer 1 Einleitung Michael Faraday war davon überzeugt, dass die Spektrallinien des Lichtes durch ein starkes Magnetfeld beeinflusst werden. Faradays Intuition ging selten fehl und am 12. März 1862 im Alter von 70 Jahren versuchte er, den Einfluss magnetischer Felder auf die Spektrallinien nachzuweisen. Leider erfahren wir aus seinen Notizen: „Nicht die kleinste Spur des erwar‐
teten Effekts.....konnte beobachtet werden“. Als P. Zeeman in Leiden 34 Jahre später mit Hilfe bedeutend stärkerer Magnetfelder und höher auflösender Spektralapparate entdeckte, dass die Spektrallinien tatsächlich in Komponenten aufgespalten werden, wenn man die Lichtquelle zwischen die Pole eines Elektromagneten bringt, war dies eine wissenschaftliche Sensation ersten Ranges. Sie fällt zeitlich etwa zusammen mit der Entdeckung der Röntgen‐
strahlen (1895), der Entdeckung der Radioaktivität (1895) und der Entdeckung des Elektrons (1897). Die Wirkung des Magnetfeldes auf die Spektrallinien wurde daher bald mit der Bewegung der Elektronen in Atomen in Verbindung gebracht und H.A. Lorentz schlug eine Beschreibung des Zeeman‐Effektes vor, die durch ihre Anschaulichkeit und Farbigkeit beein‐
druckt. Es mag verwundern, dass sein einfaches Modell eines um den Atomkern umlaufen‐
den Elektrons alle empirischen Befunde des sogenannten normalen Zeeman‐Effektes ein‐
schließlich der beobachteten Polarisationserscheinungen zwanglos erklärt. In den meisten Fällen ist dagegen das Aufspaltungsbild wesentlich komplizierter und linienreicher. Bei der Deutung dieses nur aus historischen Gründen als anomal bezeichneten Zeeman‐Effektes zeigt sich eindrucksvoll die Überlegenheit der Quantenmechanik. So ist es kaum verwunder‐
lich, dass das Studium der Zeeman‐Aufspaltung unsere heutigen Vorstellungen über atomare Eigenzustände, aber auch über die Wechselwirkung der Atome mit äußeren Strahlungsfel‐
dern stärker geprägt hat als irgendeine andere Erscheinung. Historisch lieferte z.B. die Zirkularpolarisation der Zeeman‐Komponenten einen ersten Hinweis auf den Spin des Photons in Bezug auf dessen Ausbreitungsrichtung. Auch heute wird die Zeeman‐Aufspal‐
tung intensiv untersucht, sei es zur Vermessung solarer bzw. galaktischer Magnetfelder oder sei es um atomaren Energiezuständen die richtigen Quantenzahlen zuzuordnen. Das hier be‐
schriebene Praktikumsexperiment erlaubt es, das Wirken der wichtigsten quantenmecha‐
nischen Gesetze (Betrags‐ und Richtungsquantelung, Auswahlregeln, Aufhebung der Entartung durch Symmetrieminderung, Vektormodelle der Spin‐Bahn‐Kopplung, ...) unmittelbar zu beobachten. Voraussetzung dafür ist ein Spektralapparat mit einem spektralen Auflösungsvermögen von 105 bis 106. Hier findet ein Interferometer Anwendung, wie es 1897 von den französischen Physikern Charles Fabry und Alfred Pérot entwickelt wurde. 1 2 Aufgabenstellung 2.1 Charakterisierung des Magnetfeldes 2.1.1 Die magnetische Flussdichte B ist in Abhängigkeit vom Spulenstrom zu bestimmen und zu diskutieren. 2.1.2 Die Ortsabhängigkeit des Magnetfeldes ist zu untersuchen. 2.2 Ebenes Fabry‐Pérot‐Interferometer 2.2.1 Für eine Interferometereinstellung sind aus dem Interferenzbild monochromatischer Strahlung der Spiegelabstand, die maximale Ordnung, der freie Spektralbereich und die Finesse zu bestimmen. 2.2.2 Der Einfluss des Spiegelabstandes auf die spektralen Eigenschaften des Fabry‐Pérot‐ Interferometers ist zu untersuchen. Insbesondere ist die Auswirkung auf das spektrale Auflösungsvermögen vergleichend darzustellen. 2.3 Zeeman – Aufspaltung 2.3.1 Von einer gegebenen Spektrallampe ist eine Spektrallinie zur Untersuchung des normalen Zeeman‐Effektes auszuwählen. Folgende Untersuchungen sind durchzuführen: ‐ Polarisationsanalyse für transversale und longitudinale Beobachtungsrichtung. ‐ die Aufspaltung der Linie ist in Abhängigkeit vom Magnetfeld / Spulenstrom bei transversaler und longitudinaler Beobachtungsrichtung fotografisch zu dokumentieren. ‐ Aus der magnetfeldabhängigen Zeeman‐Aufspaltung Δλ(B) ist die spezifische Ladung des Elektrons zu ermitteln. Der Vergleich mit dem Literaturwert soll zu einer Einschätzung der Messergebnisse führen. 2.3.2 Der anomale Zeeman – Effekt ist an einer geeigneten Spektrallinie qualitativ zu unter‐
suchen. Das Interferometer ist dabei so einzustellen, dass das Liniensystem optimal dargestellt wird. Die Anzahl der Komponenten ist mit der nach der Theorie zu erwar‐
tenden zu vergleichen. Der Paschen‐Back‐Effekt ist zu überprüfen. 3 Physikalische Grundlagen 3.1 Der normale Zeeman ‐ Effekt In einem äußeren Magnetfeld wird die 2
1 fache Entartung der Energieniveaus der Singulettatome 0
aufgehoben. Benachbarte, aus der selben Bahndrehim‐
pulsquantenzahl L hervorgehende Energieniveaus haben die gleiche von L unabhängige Energiedifferenz Δ
· . Infolge dieser für beide Zustände des atomaren Übergangs gleich großen Aufspaltung fallen unabhängig von der Zahl der Termkomponenten alle Über‐
gänge mit gleichem Δ zusammen; es entstehen drei Linien, das sog. normale Zeeman‐
Triplett (s. Abb. 1). 2 Abb. : 1 Zeeman‐
Triplett am Beispiel der roten Cd‐Linie Die Energiedifferenz zwischen benachbarten Linien des Zeeman‐Tripletts beträgt · Δ
·
Mit Δ
1
·
· 2
1
·
·
·
Δ
folgt für die transversale Zeeman ‐ Aufspaltung Δ
Bei einer magnetischen Flussdichte von rote Cd‐Linie Δ
, ·
·
· , ·
, ·
· ·
·
·
4
100
100 · 10
· 100 · 10
2 · 10
ergibt sich für die 0,002
! . Die quantitative Untersuchung der Zeeman‐Aufspaltung erfordert somit ein spektrales Auflösungsvermögen von mindestens ,
,
325000 . 3.2 Zur Polarisation der Zeeman‐Komponenten Die Polarisationseigenschaften der beiden frequenzverschobenen Zeeman‐Komponenten sind eine unmittelbare Folge des Photonenspins in Ausbreitungsrichtung, der Drehim‐
pulserhaltung des Systems Elektron‐Photon und der Richtungsquantelung des atomaren Bahndrehimpulses in einem äußeren homogenen Magnetfeld : 3 mit . Fällt eine zirkular polarisierte Lichtwelle in z‐Richtung auf ein Atom im Magnetfeld 0,0,
, so übertragen bei ‐Polarisation alle Photonen den Spin und bewirken der atomaren Drehimpulskomponen‐
daher bei ihrer Absorption eine Änderung Δ
te, d.h. es treten zwischen atomaren Zuständen Übergänge auf, mit Δ
1. Bei ‐Polarisation werden Übergänge mit Δ
1 induziert. Entsprechendes gilt für die Emission: Bei Übergängen mit Δ
beobachtet man in Feldrichtung emittiertes zirkular polarisiertes Licht mit ‐ und bei Übergängen mit Licht mit ‐ Polarisation, das bei transversaler Beobachtung als senkrecht zur Δ
Feldrichtung linear polarisiert erscheint. Durch den Übergang Δ
0 wird die ursprüngliche, unbeeinflusste Linie emittiert. Der Übergang Δ
0 kann also nur mit dem vom ‐Feld nicht beeinflussten Bewegungsanteil des Elektrons in Feldrichtung korrelieren. Daher wird die ursprüngliche, unbeeinflusste Linie emittiert. Ein in z‐Richtung oszillierender elektrischer Dipol emittiert eine in dieser Richtung linear polarisierte elektromagnetische Strahlung. Die mittlere ‐Komponente des Zeeman‐Tripletts offenbart sich mithin nur bei transversaler Beobachtung. 3.3 Der anomale Zeeman‐Effekt und der Paschen‐Back‐Effekt Im allgemeinen Fall kann nicht davon ausgegangen werden, dass 0 gilt. Somit hängt das resultierende magnetische Moment neben der Quantenzahl des Gesamtdrehimpulses auch von den Bahndrehmoment‐ und Spinmomentquantenzahlen des betreffenden Zustandes ab, was mit dem g‐Faktor ausgedrückt wird. 1
1
1
, ,
1
2
1
Für ein freies Elektron ist 1 1
, 0,
2. 2 2
In einem nicht zu starken äußeren Magnetfeld ergibt sich die energetische Aufspaltung der Zeeman‐Niveaus von ∆
· ·
· Beispiel: Cadmium‐Atom, Übergang von nach , λ = 508,5820 nm 1,0,1
2 und 1
2,1,1
2
Die beiden Zustände spalten also im Magnetfeld unterschiedlich stark auf, was zu einer größeren Linienvielfalt Anlass gibt (s. Abb.2). 4 Abb. 2: Anomaler Zeeman‐Effekt und Entwicklung des Paschen‐Back‐Effektes am Übergang des Cd‐Atoms (schemat.) Die neun äquidistanten anomalen Zeeman‐Linien des betrachteten Übergangs mit den oben beschriebenen Polarisationseigenschaften haben den extrem ·
kleinen aus Abb. 2 ablesbaren Frequenzabstand Δ
. Dies entspricht Δ
0,0012
bei B = 100mT. Der sich hier zeigende zusätzliche Einfluss des Elektronenspins ist eigentlich der vollständige atomphysikalische Normalfall, so dass die Bezeichnung „anomaler Zeeman‐Effekt“ ungerechtfertigt ist. Doch war zu der Zeit, als H. A. Lorentz sein Modell zur Erklärung einiger Erscheinungen des Zeeman‐Effektes vorstellte, der Elektronenspin noch nicht bekannt. Daher spricht man auch noch heute im Falle S=0, der eigentlich ein Sonderfall ist, vom „normalen Zeeman‐Effekt “. Wie aus dem Beispiel hervorgeht, ist die Aufspaltung i.a. kleiner als beim normalen Effekt. Aber auch starke Magnetfelder begünstigen nicht unbedingt die Beobachtung des anomalen Effektes, weil durch die wachsende Wechselwirkung der magnetischen Bahn‐ und Spinmomente mit dem äußeren Magnetfeld die L‐S‐Kopplung zunehmend aufgebrochen ,
2
· der Zeeman‐Niveaus vom g‐
wird. Damit wird die Energie Faktor unabhängig, so dass auch die Zeeman‐Aufspaltung wieder ein ganzzahliges Vielfaches · beträgt (z.B. 2
· bzw. 1
bzw. von · für die oben betrachteten Cd‐Terme ). Unter Beachtung der Auswahlregel vereinfacht sich mit wachsender Feldstärke das Aufspaltungsbild, bis schließlich nur noch das normale Zeeman‐Triplett verbleibt (Paschen‐ Back‐Effekt). 5 3.4 Das ebene Fabry‐Pérot‐Interferometer Das Fabry‐Pérot‐Interferometer wird in der Spektroskopie zur Trennung sehr nahe bei‐
einander liegender Spektrallinien benutzt. Die hierzu notwendige Auflösung wird durch Vielstrahlinterferenz erreicht. (Abb. 4) Abb. 4: Strahlengang im Fabry‐Pérot‐Interferometer Zwischen zwei aufeinanderfolgenden Teilwellen besteht eine konstante optische Weglängendifferenz Δ
; k ‐ ganzzahlig ; ( Maximumbedingung ) 2
· cos
Bei sehr großer Bündelzahl, theoretisch bei unendlich vielen Bündeln, entstehen scharfe und intensitätsstarke Ringe auf dunklem Untergrund. Bei endlicher Bündelzahl p liegen zwischen den Hauptmaxima noch p – 2 Nebenmaxima, so dass (s. Abb. 5) der Abstand zwischen einem Hauptmaximum und dem benachbarten Minimum etwa 6 beträgt. Transmission
2d cosδ
kλ
(k+1) λ
Abb. 5: Intensitätsverlauf für p=8 ; (schematisch) Sind und Δ zwei benachbarte Wellenlängen, so wird es von der Breite der Interferenzstreifen abhängen, ob man die zu ihnen gehörigen Interferenzringe noch getrennt sieht oder nicht. Fällt das Hauptmaximum von Δ auf das erste Minimum von , so kann man gerade noch getrennte Interferenzringe erkennen, während dies bei noch größerer Annäherung fraglich wird. Die Bedingung für das Auflösungsvermögen A ist somit: 1
Δ
Δ
Das Auflösungsvermögen A des Gerätes ist der Ordnung k und der Zahl p der interferie‐
renden Bündel proportional. Da die Ordnung mit der Dicke der Luftschicht wächst, die bei den Interferometern einige Millimeter stark ist, ist die Ordnung k sehr hoch. Die Zahl der interferierenden Bündel ist dagegen nur mäßig. Mit 1, d = 2mm, und 650
liegt in der Mitte 0 ein Maximum der Ordnung 6 · 10 . Mit p = 40 ergibt sich ein Auflösungsvermögen von etwa 2 · 10 . Es können also Wellenlängenunterschiede von Δ
4 · 10
noch getrennt werden. Obwohl man mit diesem Interferometer damit die höchste bislang überhaupt erreichbare Auflösung erzielt, so reicht diese doch gerade noch aus, um die Zeeman‐Aufspaltung quantitativ zu untersuchen. Das spektrale Auflösungsvermögen A, d.h. die Halbwertsbreite der Transmissionskurve ∆ , lässt sich durch Variation des Plattenabstandes verändern. Gleichzeitig verändert sich auch der freie Spektralbereich . Der Quotient aus freiem Spektralbereich und Halbwertsbreite liefert die Finesse F* des Fabry‐Pérot‐Interferometers. 7 4 4.1 Zum Messverfahren Experimentelle Anordnung 1 , 2 Feldspulen und Polschuhe des Weißschen Magneten 3 drehbare Grundplatte zur wahlweise transversalen oder longitudinalen Beobachtung des Zeeman‐Effektes 4 Gasentladungslampe mit Vorschaltdrossel 5 Fabry‐Pérot‐Interferometer, Typ KFPI, mit Beobachtungsfernrohr und schwenkbarem Spiegel zur visuellen Beobachtung 6 7 Digitalkamera mit Zoomobjektiv Bedienelemente des piezoelektrischen Stellelementes zur Paralleljustierung der Fabry‐
Pérot‐Platten (greift an drei um 120° versetzte Randpunkte eines Spiegels an) 8 Spannungsversorgungsgerät (600 V) für piezoelektrisches Stellelement 9 Stellgleichrichter (max. 11 A) zur Stromversorgung des Weißschen Magneten Weitere Hilfsmittel : ‐ Teslameter mit Hallsonde zur Magnetfeldmessung ‐ verschiedene Filter zur Selektion von Spektrallinien ‐ Polarisationsfilter und λ / 4 ‐Plättchen zur Untersuchung der Polarisationseigen‐
schaften der Zeeman‐Komponenten 4.2 Zur Messung der Zeeman ‐ Aufspaltung Aus Abb. 5 ist unmittelbar abzulesen: 2 cos
maximum k‐ter Ordnung) mit 1
cos
(Bedingung für das Interferenz‐
1
1
·
2
1
1
2
Differenzieren nach 1
liefert: 8
2
·
4
Mit der Näherung und dem Mittelwert 8 , 8
wobei bzw. den Durchmesser der Außen‐ bzw. der Mittelkomponente des k‐ten Ringsystems (bei transversaler Beobachtung) bedeuten, wird 2 ·
2
Δ
Δ
·
·
4
4
2
Δ
8
4.3 Registrierung der Interferenzmuster Das FPI wird jeweils mit mechanischen Stellschrauben bestmöglich voreingestellt. Die Feinjustierung erfolgt über Piezoelemente oder PC‐gekoppelte Stellmotoren. Das Interferenzmuster kann dabei in der live‐Vorschau einer Digitalkamera auf dem PC‐
Monitor beobachtet werden. Durch dieses Vorgehen ist eine berührungslose Einstellung möglich. Die Interferenzmuster werden mit der Digitalkamera per Remote‐Bedienung fotografiert. Die Kamera befindet sich im „Manuell“‐Modus. Wählen Sie optimale Betriebsparameter. Eine separate Bildauswertung (z.B. mit Software „Image Viewer“) liefert Intensitätsprofile und Ringdurchmesser. Erfragen Sie die Parameter des verwendeten Kamerachips beim Betreuer. 5 [1] Hänsel / W. Neumann, Physik, Band III: Atome, Atomkerne, Elementarteilchen, Akadem. Verlg. 1995. H. Haken, H. C. Wolf, Atom ‐ und Quantenphysik, 6. Auflg, Springer Verlag, Berlin, Heidelberg, New York Bosch, J.C. van den, The Zeeman Effect, in: Handbuch der Physik, Hrsg. S. Flügge, Band 28, Berlin, Göttingen, Heidelberg, Springer Verlag, 1957, S.296 – 332. Demtröder, W., Experimentalphysik 2 – Elektrizität und Optik, Springer Verlag, Berlin, Heidelberg, New York, 1995 [2] [3] [4] Literatur 9