Document

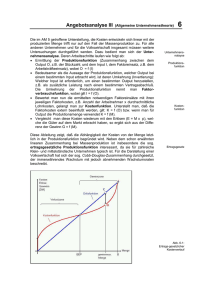
Ökonomie der Unternehmen
• Ziel der Unternehmen: • Unter anderem Gewinnmaximierung
• G(x) = p*x - K(x) = p+x - (kfix + kvar (x))
• Gewinn = Erlös - Kosten
• Strategiemöglichkeiten um Gewinn zu verändern: • Preise steuern (senken, erhöhen)
• Mengen steuern (senken, erhöhen)
• Kosten steuern (sind abhängig von der Produktionsmenge)
• Angebotskurve zeigt die Strategie der Unternehmen, bei steigendem
•
Preis (unter der Annahme, der Preis sei erst mal nicht beeinflussbar)
mehr Menge produzieren, um damit eine Ertragssteigerung zu erreichen. Die Möglichkeit eine bestimmte Strategie zu wählen ist vor allem
abhängig von: • der Marktform (z.B. Monopol, Oligopol, Polypol) und der • Marktstruktur (Anzahl der Anbieter/Nachfrager; Möglichkeit der Produktdifferenzierung, Preiskontrolle) • Ein Unternehmen kann beispielsweise bei vollkommener Konkurrenz
(Viele Anbieter/Viele Nachfrager + homogenes Gut) nur die Strategie
des Mengenanpassers verfolgen
151
Aggregation der Angebotsfunktion
Kapitel 8
(a) Angebot von
Unternehmen A
P
(c) Marktangebot
P
s
80
80
60
60
60
40
20
0
4
s
5
10
15
Menge A (in Tausend)
40
20
qA
0
Preis (US-$)
80
Preis (US-$)
Preis (US-$)
(b) Angebot von
Unternehmen B
s
P
225
Analyse des Marktes bei vollkommenem Wettbewerb
11
4
11
Marktangebotskurve
20
s
5
10
15
Menge B (in Tausend)
40
S
S
qB
0
5
10
15
20
25
Gesamtmenge (in Tausend)
Q = qA + qB
Abbildung 8-4: Durch Addition aller Angebotskurven der Unternehmen können wir das Marktangebot ableiten
Die Diagramme zeigen, dass sich die Marktangebotskurve (SS) aus zwei Einzelangebotskurven (ss) zusammensetzt. Wir addieren die von jedem Unternehmen bei einem Preis von US-$ 40 angebotenen Mengen horizontal
und erhalten das Marktangebot bei einem Preis von US-$ 40. Dasselbe gilt für jeden Preis und jede beliebige
Anzahl von Unternehmen. Gäbe es 1.000 Unternehmen, die mit A identisch sind, würde die Marktangebotskurve
aussehen wie die Angebotskurve von Unternehmen A bei einer tausendfachen Vergrößerung des Maßstabs
auf der X-Achse.
Konkurs gehen, wenn sie nicht mehr imdie Dramatik von Ein- und Austritten nicht
stande sind, ihre Rechnungen zu bezahlen. 152 immer perfekt widerspiegeln, ist die zuWir sprechen von freiem Markteintritt und
grunde liegende Logik von P, MC und AC
von Dividenläufig die Marktpreise für Weizen oder Öl,
zahlt, den es
die sie produzieren.
elle AusstatWir können uns
Mengenanpasser
em es selbst
Unternehmenssituation
beieinen
vollkommener
Konkurrenz
(Preisnehmer) im vollständigen Wettbewerb
n. Alle diese
es Unterneh-
ordert ein efnen Abläufe
wendung verfiziente Pround kluge
der richtigen
zu geringstder optima-
e sowohl die
Rolle spielen,
stenstruktur
e erzielen zu
(a) Branche
(b) Unternehmen
P D
S
P
d
d
A
S
Branchenproduktion
D
Q
q
Unternehmenproduktion
Abbildung 8-1: Die Nachfragekurve ist für ein Unternehmen im vollständigen Wettbewerb vollkommen
elastisch
Die Branchennachfragekurve
links zeigt die unelas153
Produktion und Kosten
• Die Kosten bestimmen
•
Lage und Verlauf der
Angebotskurve und
beeinflussen
Marktgleichgewicht. Kosten
• Die Kosten eines Gutes
bestehen aus dem, was man für
den Erwerb dieses Gutes aufgibt.
(Opportunitätskostenbegriff).
• Kosten sind Güterverzehr zur
Erstellung der betrieblichen
Leistung (betriebswirtschaftliche
Definition)
154
Produktion und Kosten
Anzahl der
Arbeiter
Output (Kekse
pro Stunde)
Grenzprodukt
der Arbeit
Kosten der
Fabrik (€)
Kosten der
Arbeiter (€)
Gesamtkosten des
Faktoreinsatzes (€)
0
0
-
30
0
30
1
50
50
30
10
40
2
90
40
30
20
50
3
120
30
30
30
60
4
140
20
30
40
70
5
150
10
30
50
80
!
• Der Output, also die produzierte Menge (Stücke) x, hängt vom Input ab, also von den eingesetzten
•
•
•
•
•
•
Produktionsfaktoren (Arbeit, Boden, Kaptial)
Im folgenden Beispiel ist die Produktionsfunktion in Abhängigkeit des eingesetzten Produktionsfaktors
Arbeit dargestellt. Alle anderen Produktionsfaktoren bleiben gleich groß, sind also konstante Faktoren. These 1: Je höher der eingesetzte Faktor Arbeit, desto höher der Output. These 2: Das Grenzprodukt der Arbeit (zusätzliche Ertrag (Output) pro eingesetztem Faktor) sinkt
These 3: Die Kosten der Fabrikanlage sind konstant (Fixkosten = 30)
These 4: Je höher der eingesetzte Faktor Arbeit, desto höher die Kosten für alle Arbeitskräfte
These 5: Je höher der eingesetzte Faktor Arbeit, desto höher sind die Gesamtkosten
155
Produktionsfunktion und Grenzprodukt
ProduktionsMenge/Output
• Produktionsfunktion = Produktionsfunktion
(Kekse pro Stunde)
150
140
130
•
120
110
100
90
80
70
60
50
•
40
30
20
10
0
1
2
3
4
5
Anzahl beschäftigter
Mitarbeiter (Input)
156
Zusammenhang zwischen
Produktionsfaktoreinsatz und
Output
Grenzprodukt = Output
(produzierte Menge), der
durch eine zusätzliche Einheit
an Input (Faktoreinsatz)
erzielt wird
Abnehmendes GP =
abnehmender Zuwachs an
Output durch zusätzlichem
Input(Faktoreinsatz) abhängig
von der Anzahl der
produzierten Menge
Produktion und Kosten
Kosten der
Fabrik (€)
Kosten Gesamtkosten des
der
Faktoreinsatzes
Arbeiter
(€)
(€)
Gesamtkosten(€)
80
Gesamtkostenkurve
70
30
0
30
60
30
10
40
30
20
50
50
40
30
30
30
60
30
40
70
30
50
80
20
10
0
10 20 30 40
50
60 70
80 90
100
110 120 130 140
150
Produktionsmenge
(Kekse pro Stunde)
157
Produktionsfunktion und Gesamtkosten
ProduktionsMenge/Output
Gesamtkosten(€)
Produktionsfunktion
(Kekse pro Stunde)
150
80
140
130
Gesamtkostenkurve
70
120
60
110
100
50
90
80
40
70
60
30
50
40
20
30
20
10
10
0
1
2
3
4
5
0
Anzahl beschäftigter
Mitarbeiter (Input)
158
10 20 30 40
50
60 70
80 90
100
110 120 130 140
150
Produktionsmenge
(Kekse pro Stunde)
Überblick Definition Kosten
Kosten
Explizite Kosten
Implizite Kosten
Kosten = Marktwert der
Inputfaktoren einer Unternehmung.
Die Inputfaktoren werden zur
Erstellung von (Output) Produkten
benötigt
K(x), K(q) gleiche
Bedeutung
unterschiedliche
Annotation
implicit costs
Costs that require an outlay of
money by the firm
explicit costs
Costs that do not require an outlay
of money by the firm
Fixe Kosten
Kosten die nicht mit der
Produktmenge variieren
kfix
Fixed costs
Costs that do not vary with the
quantity of output produced
FC
Variabel Kosten
Kosten die mit der Produktmenge
variieren
kvar(x), kvar(q)
Variable costs
Costs that do vary with the quantity
of output produced
VC
Gesamtkosten
Fixe und variable kosten
K(x) = kfix+ kvar(x),
K(q) = kfix+ kvar(q)
Total costs
The market value of all the inputs
that a firm uses in production
TC
Durchschnittskosten,
Stückkosten,
Durchschnittliche
Gesamtkosten
Kosten je Produkteinheit (Kosten
pro Mengeneinheit, pro Stück)
DK,
Average total
cost
Total cost divided by the quantity of
output
ATC
Fixed costs divided by the quantity
of output
AFC
K
Durchschnittliche fixe Kosten Fixkosten je Produkteinheit
kfix ／x
Average fixed
cost
Durchschnittliche variable
Kosten
Variable Kosten je Produkteinheit
kvar(x)／x
Average variable Variable costs divided by the
cost
quantity of output
AVC
Grenzkosten
Anstieg der Gesamtkosten durch
eine zusätzliche Produkteinheit
(Mengeneinheit, zusätzliches Stück)
∆K／∆ x
Marginal cost
MC
159
The increase in total cost that arises
from an extra unit of production
Produktion Limonade - Kosten berechnen!
Menge
Limonade
Gesamtkosten (K)
Fixe
Kosten
(FK)
Variable
Kosten (VK)
Ø fixe
Kosten
(DFK)
Ø variable K
(DVK)
Ø GesamtK
(DK)
Grenzkosten
(GK)
0
3,00
3,00
0,00
-
-
-
-
1
3,30
3,00
0,30
3,00
0,30
3,30
2
3,80
3,00
0,80
3
4,50
3,00
1,50
1,00
0,50
1,50
4
5,40
3,00
2,40
0,75
0,60
1,35
5
6,50
3,00
3,50
0,60
0,70
1,30
6
7,80
3,00
4,80
0,50
0,80
1,30
7
9,30
3,00
6,30
0,43
0,90
1,33
8
11,00
3,00
8,00
0,38
1,00
1,38
9
12,90
3,00
9,90
0,33
1,10
1,43
10
15,00
3,00
12,00
160
0,30
0,70
0,90
1,10
1,30
1,50
1,70
1,90
Produktion Limonade - Lösung
Menge
Limonade
Gesamtkosten (K)
Fixe
Kosten
(FK)
Variable
Kosten (VK)
Ø fixe
Kosten
(DFK)
Ø variable K
(DVK)
Ø GesamtK
(DK)
Grenzkosten
(GK)
0
3,00
3,00
0,00
-
-
-
-
1
3,30
3,00
0,30
3,00
0,30
3,30
2
3,80
3,00
0,80
1,50
0,40
1,90
3
4,50
3,00
1,50
1,00
0,50
1,50
4
5,40
3,00
2,40
0,75
0,60
1,35
5
6,50
3,00
3,50
0,60
0,70
1,30
6
7,80
3,00
4,80
0,50
0,80
1,30
7
9,30
3,00
6,30
0,43
0,90
1,33
8
11,00
3,00
8,00
0,38
1,00
1,38
9
12,90
3,00
9,90
0,33
1,10
1,43
10
15,00
3,00
12,00
0,30
1,20
1,50
161
0,30
0,50
0,70
0,90
1,10
1,30
1,50
1,70
1,90
2,10
Limonade - Gesamtkosten
Menge Limonade
Gesamtkosten (K)
15.00
Gesamtkosten(€)
14.00
13.00
0
3,00
1
3,30
2
3,80
3
4,50
4
5,40
5
6,50
6
7,80
7
9,30
4.00
8
11,00
3.00
9
12,90
2.00
10
15,00
12.00
11.00
10.00
9.00
8.00
7.00
6.00
5.00
Gesamtkostenkurve
1.00
0
162
1
2
3
4
6
7
8
9
5
10
Produktionsmenge
Produktion Limonade - Grenzkosten
Menge GesamtLimo- kosten (K)
nade
Kosten (€)
3.50
3.25
3.00
0
3,00
1
3,30
2
3,80
3
4,50
4
5,40
5
6,50
6
7,80
0.75
7
9,30
0.50
8
11,00
0.25
9
12,90
10
15,00
2.75
2.50
GK (GrenzKosten)
2.25
2.00
1.75
1.50
1.25
1.00
0
1
2
3
4
5
6
7
8
10
9
Produktionsmenge (Q)
Grenzkosten
(GK)
0,30
0,50
0,70
0,90
1,10
1,30
1,50
1,70
1,90
2,10
• Steigende Grenzkosten reflektieren die Eigenschaft der Produktionsfunktion, dass das Grenzprodukt fällt. • Warum hat die Grenzkostenkurve eine positive Steigung?
163
Durchschnittskosten
Meng
e
Limonade
Fixe Variabl Ø fixe
Ø
Koste
e
Koste varin (FK) Kosten
n
able K
(VK) (DFK) (DVK)
0
3,00
0,00
-
-
1
3,00
0,30
3,00
0,30
2
3,00
0,80
1,50
0,40
3
3,00
1,50
1,00
0,50
4
3,00
2,40
0,75
0,60
5
3,00
3,50
0,60
0,70
6
3,00
4,80
0,50
0,80
7
3,00
6,30
0,43
0,90
8
3,00
8,00
0,38
1,00
9
3,00
9,90
0,33
1,10
10
3,00
12,00
0,30
1,20
Kosten(€)
3.50
3.25
3.00
2.75
2.50
2.25
2.00
1.75
1.50
1.25
DVK
1.00
0.75
0.50
DFK
0.25
0
1
2
3
4
5
6
7
8
9
10
Produktionsmenge (Q)
164
Durchschnittskosten
• U-förmiger Verlauf:
• Bei sehr geringem Outputniveau
Kosten (€)
3.50
3.25
3.00
2.75
2.50
•
2.25
2.00
1.75
DK
1.50
1.25
DVK
1.00
•
0.75
0.50
DFK
0.25
0
1
2
3
4
5
7
8
10
6
9
Produktionsmenge (Q)
165
sind die Durchschnittskosten relativ
hoch (die fixen Kosten verteilen
sich auf wenige Outputeinheiten). Mit steigendem Output fallen die
Durchschnittskosten (weil die
durchschnittlichen fixen Kosten
stark fallen). Ab einer bestimmten
Ausbringungsmenge steigen die
Durchschnittskosten: Der Einfluss
der (fallenden) fixen Kosten sinkt
und die steigenden variablen Kosten
treiben die Durchschnittskosten
nach oben.