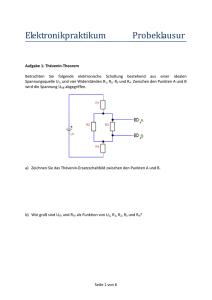
Skript

PRAKTIKUM ELEKTROTECHNIK
Institut für Mikroelektronik und Mikrosensorik
15. Auflage, 2013
Alle Rechte vorbehalten
Johannes Kepler Universität Linz, Institut für Mikroelektronik und Mikrosensorik
A-4040 Linz • Altenberger Straße 69 • Internet: http://www.ime.jku.at/ • DVR 0093696
Einleitung
Dieses Skriptum zum Praktikum Elektrotechnik soll den Studierenden die über die theoretischen Grundkenntnissen aus der Vorlesung hinausgehenden Kenntnisse zur Durchführung der
Übungen vermitteln. Auf langwierige Ableitungen und Erklärung von Details ist in den vorliegenden Unterlagen weitgehend verzichtet worden. Sie werden in der angeführten Literatur
sowie in entsprechenden Folgevorlesungen behandelt. Falls Sie trotz dieses Skriptums (oder
vielleicht gerade deswegen) Probleme mit dem grundlegenden Verständnis haben, wenden Sie
sich bitte an einen Übungsbetreuer (wenn möglich schon vor der Übung).
Der Schwerpunkt in den Übungen liegt in der praktischen Anwendung einfacher und grundlegender Zusammenhänge. Messtechnische Probleme werden nur soweit behandelt, als sie die
Übungsdurchführung direkt betreffen. Da die Zeit bei manchen Übungen knapp bemessen ist,
überlegen Sie sich vor den Messungen, welche Messpunkte wirklich interessant sind (sofern
diese nicht schon vorgegeben sind), und bauen Sie die Schaltungen möglichst übersichtlich auf,
um den Betreuern die Überprüfung zu erleichtern.
Organisatorisches
Bevor Sie mit Ihrer ersten Übung beginnen, geben Sie bitte die unterschriebene Kenntnisnahme
der Sicherheitsbestimmungen beim Übungsleiter ab.
Am Beginn jeder Übung findet ein schriftlicher Test zum Stoffgebiet der aktuellen sowie der
vorangegangenen Übungen statt (was konsequenterweise auch den Stoff der Vorlesungen und
Übungen Elektrotechnik 1 und 2 inkludiert!).
Als Vorbereitung dienen die am Ende jedes Kapitels angeführten Kontrollfragen.
Ein positives Testergebnis ist für die Übungsdurchführung Voraussetzung. Bei einer negativen
Beurteilung werden sie von der weiteren Teilnahme am Praktikum ausgeschlossen.
Vor dem ersten Praktikumstermin wird eine Zuteilung der Termine veröffentlicht. Nach dieser
Zuteilung ist eine Verschiebung ihrer Termine nur möglich, indem sie ihren Termin mit jemandem tauschen. Derartige Wechsel dürfen sie nach Belieben durchführen, sie müssen jedoch am
Beginn der Praktikumsübung den Übungsbetreuer darauf hinweisen.
Die Praktikumsübungen werden in Zweiergruppen durchgeführt. Die Einteilung der Gruppen
erfolgt jeweils am Beginn einer Übung und gilt nur für die jeweilige Übung.
Am Ende jeder Übung ist die Kopie der Mitschrift der Messwerte (Urprotokoll) einem Übungsbetreuer zu übergeben.
Während des Praktikums dürfen keine alten Protokolle verwendet werden. Auch beim Verfassen
des Protokolls dürfen keine Vorlagen aus früheren Jahrgängen verwendet werden. Beschreiben
Sie IHRE Meinung und IHRE Überlegungen. Die Abgabe eines Plagiats führt unweigerlich zu
einer negativen Beurteilung.
2
Protokolle
Für jede Übung ist von jedem Team ein Protokoll auszuarbeiten, welches spätestens eine Woche
nach der Übung abzugeben ist1.
Das Protokoll hat zu enthalten:
• Deckblatt (aktuelle Version auf www.ime.jku.at>Teaching>Praktikum Elektrotechnik)
• Aufgabenstellung (kurz und in eigenen Worten, keine Kopie aus dem Skript)
• Berechnungen zur Dimensionierung (wenn notwendig)
• Messschaltung, Erklärung was, wie und warum so und nicht anders gemessen wurde
(wenn notwendig), sowie verwendete Messgeräte
• Tabelle mit Messwerten (mit Einheiten!) und daraus berechnete Größen
• Berechnungen zur Auswertung der Ergebnisse
• Diagramme mit ausreichender Beschriftung, wie in Abbildung 1 gezeigt.
• Bemerkungen und Erklärungen (speziell wenn unerwartete Messergebnisse aufgetreten
sind, soll versucht werden, diese zu interpretieren).
Fertigen sie die Protokolle entsprechend den Richtlinien ab Seite 4 an.
Wenn Sie Anregungen, Kritik, Beschwerden usw. bezüglich des Skriptums und der Übungsinhalte haben, ersuchen wir Sie diese zu äußern, damit wir die Qualität der Lehrveranstaltung
verbessern können. Bitte nutzen Sie die die Evaluierung der Lehrveranstaltung im KUSSS!
1 Sie
können das Protokoll entweder im Sekretariat abgeben oder in den Postkasten des Instituts (im Erdgeschoß, Aufschrift ’Prof. Jakoby’ einwerfen).
Laborordnung und Sicherheitsbestimmungen
1. Überprüfen Sie vor dem Übungsbeginn, ob alle Steckbretter und dgl. vollständig bestückt
sind.
2. Führen Sie alle Schaltungsum- oder -aufbauten, sofern möglich, im spannungslosen Zustand durch.
3. Bauen Sie die Schaltungen übersichtlich auf und verwenden Sie verschiedenfärbige Leitungen für verschiedene Signale.
4. Beschriften Sie keinenfalls Geräte und berühren sie Oszilloskop und Messgeräte nicht
mit Schreibgeräten oder harten Gegeständen.
5. Vermeiden Sie alles, was Geräten und Bauteilen schaden könnte. Eventuell auftretende
Schäden sind sofort dem Übungsleiter zu melden.
6. Überprüfen Sie vor dem Einschalten, ob bei den Messgeräten der richtige Messbereich
gewählt wurde und ob sie richtig angeschlossen sind. Beachten Sie, dass bei den am
Übungsplatz vorhandenen Multimetern die Anschlüsse für Strom- und Spannungsmessung verschiedene sind!
7. Schalten Sie die Multimeter während der Umbauten und am Ende der Übung ab, um
Batterie zu sparen.
8. Beachten Sie bei jeder Übungsanordnung die entsprechenden Grenzwerte!
9. Bringen Sie am Ende einer Übung die Steckbretter in jenen Zustand, in dem Sie sie übernommen haben. Der Übungsleiter muss die Vollständigkeit der Messgeräte und Bauelemente kontrollieren.
4
Richtlinien für Praktikumsprotokolle
Grundlagen
• Schreiben Sie das Protokoll für jemanden, der die theoretischen Grundlagen beherrscht.
Geben Sie ihm die Information, die nötig ist, um die Übung in möglichst kurzer Zeit
gedanklich oder experimentell nachvollziehen zu können.
• Beschreiben Sie kurz die wichtigsten physikalischen Prinzipien und Größen dieser Übung.
• Keine allgemeine Lehrbuchtheorie zum Thema, keine Abschreibübung aus der Übungsanleitung.
• Geben Sie Gleichungen an, mit denen Sie Ihre Messungen später auswerten. Nummerieren der Formeln erleichtert im Folgenden das Verweisen auf sie.
• Keine Ableitungen oder Beweise. (Können eventuell in einem Anhang gebracht werden.)
Messschaltung
• Skizzieren Sie sauber (mit Lineal) die Messschaltung, ohne Schnörkel (Hinterlegung,
Schatten etc.).
• Erläutern Sie eventuell notwendige Dimensionierungen.
Geräteliste
• Eine Liste der verwendeten Messgeräte (Marke, Type, Inventarnummer) ermöglicht es,
die verwendeten Geräte wiederzufinden, wenn Unstimmigkeiten bei der Auswertung der
Messergebnisse auf einen Instrumentenfehler schließen lassen, oder der Versuch mit denselben Geräten wiederholt werden soll.
Messungen
• Alle gemessenen Werte müssen im Protokoll angegeben werden, die Angabe von Mittelwerten oder Auswertungsergebnissen reicht nicht (Ausnahme: Messungen am Oszilloskop nicht in Skalenteilen sondern in Sekunden bzw. Volt). Messwerte bestehen immer
aus Maßzahl und Einheit. In jeder Tabelle muss daher auch eine Angabe der Einheit vorhanden sein. Einheiten dürfen nach DIN nicht in eckige Klammern gesetzt werden.
• Große (> 9999) und kleine (< 0,1) Zahlen werden mit Hilfe von Zehnerpotenzen dargestellt.
• Falls Größen aus anderen Quellen stammen (Übungsanleitung, Tabellenwerke, ...), so
sind diese Quellen anzugeben.
• Während der Übung sind die Messwerte auf Plausibilität zu überprüfen.
• Wählen Sie Messpunkte und Messbereich so, dass die Genauigkeit der Messung möglichst hoch ist.
5
• Bei der Berechnung von Größen sind alle verwendeten Formeln anzugeben (oder auf sie
zu verweisen). Außerdem ist darauf zu achten, dass alle eingesetzten Werte bekannt sind.
Täuschen Sie nicht durch die Angabe vieler Nachkommastellen eine größere Genauigkeit
vor, als tatsächlich vorhanden ist.
• Gewöhnen Sie sich daran, Formeln vor dem ersten Einsetzen der Messwerte anzuschreiben, auch wenn Sie die Formeln auswendig wissen. Berechnung: Formel allgemein –
Zahlen mit Einheiten eingesetzt – Ergebnis mit Einheit.
• Oberstes Prinzip ist die Nachvollziehbarkeit: Anhand Ihres Protokolls muss es möglich
sein, den gesamten Messvorgang, der zu Ihrem Endergebnis geführt hat, lückenlos zu
rekonstruieren (auch noch nach Jahren).
Diagramme
Abbildung 1: Strom durch eine Halbleiterdiode (Musterdiagramm)
• Wahl der Achsen: Abszisse (horizontale Achse): Jene Werte, die vom Experimentator
vorgegeben werden (Ursache), Ordinate (vertikale Achse): Jene Werte, die durch den
Versuch bestimmt werden (Wirkung).
• Jede Achse erhält einen Namen (Größe), eine Einheit, eine Skala und eventuell einen
Pfeil für den Wertzuwachs. Größe und Einheit werden entweder durch einen Bruchstrich
oder durch das Wort „in“ getrennt, die Verwendung eckiger Klammern ist nicht erlaubt.
Beispiele: U/V, UV , Spannung in Volt, Spannung in V, U in V.
• Die Messpunkte werden deutlich markiert (◦, !, ",#, ", ×, +, ...) und eine Ausgleichskurve darübergelegt.
• Die Ausgleichskurve muss einer physikalisch sinnvollen Funktion entsprechen. Folglich
muss die Ausgleichskurve nicht durch jeden Messpunkt verlaufen (Stichwort Messfehler).
• Falls Sie Diagramme von Hand zeichnen, achten Sie auf eine ansprechende Form (glatte
Kurven; falls nötig Kurvenlineal und Millimeterpapier benützen).
6
• Offensichtliche Ausreißer werden beim Zeichnen der Kurve nicht berücksichtigt. Stimmt
die gemessene Kurve nicht mit der Theorie überein, so ist eine Erklärung anzufügen.
• Nach Möglichkeit sollen folgende Maßstäbe verwendet werden: 1 cm =1
! Einheit, 1 cm =2
! Einheiten,
1 cm =
! 5 Einheiten, sowie Vielfache davon. Nötigenfalls sind die gewählten Maßstäbe anzugeben (sinnvoll z. B. bei Zeigerdiagrammen).
• Das Diagramm, sowie bei Kurvenscharen die einzelnen Kurven, sind zu benennen.
• Ein sauberes Diagramm, welches händisch mit Hilfe eines Kurvenlineals auf Millimeterpapier gezeichnet wurde, ist einer Computergrafik mit krummen Maßstäben und eckigen
Kurven vorzuziehen.
• Bei computergenerierten Diagrammen Gitter (Grid) verwenden, Diagrammfläche nicht
hinterlegen.
Erkenntnisse
• Die Ergebnisse der Messungen müssen kommentiert werden. Vor allem bedürfen unerwartete Messergebnisse einer Erklärung.
• Die Interpretation der Ergebnisse in eigenen Worten ist (nach der Nachvollziehbarkeit der
Experimente) am wichtigsten und für die Beurteilung des Protokolls entscheidend!
Äußere Form
• Deckblatt (Kopiervorlage liegt dem Skriptum bei)
• Aus Gründen der Lesbarkeit ist der Text der Protokolle am Computer zu schreiben. Diagramme (Messaufbau, Oszi–Bilder,...) dürfen von Hand gezeichnet werden (wird aus
Zeitgründen auch explizit empfohlen).
• Reine Maple- oder Mathematica-Ausdrucke werden nicht akzeptiert, sie können eventuell
im Anhang beigelegt werden.
• Wählen Sie einen Seitenrand von 2 cm.
• Formelzeichen werden kursiv geschrieben, Funktionen (wie cos, ln, ...) und Zahlen werden aufrecht geschrieben.
Einheiten werden aufrecht geschrieben. Beispiel: U2 = 12 V.
"
!
!!
"
!12
"
U2"
[V]
• Einheiten dürfen nicht in Klammern gesetzt werden. Beispiel: !
!=
"
"
• Zwischen Zahl und Einheit ist ein Abstand zu lassen, ebenso vor und nach einem Gleichheitszeichen.
• Schriftart und Schriftgröße sind in Text und Formeln gleich zu wählen.
• Die Protokolle sind im Original abzugeben, Kopien werden nicht angenommen. Auffallende Ähnlichkeiten mit anderen Protokollen führen zu einer negativen Beurteilung.
7
Inhaltsverzeichnis
1 Oszilloskop
1.1 Allgemeines . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Aufbau und Funktionsweise eines analogen Oszilloskops . . .
1.2.1 Elektronenstrahlröhre . . . . . . . . . . . . . . . . . .
1.2.2 Blockschaltbild . . . . . . . . . . . . . . . . . . . . .
1.2.3 Triggerung . . . . . . . . . . . . . . . . . . . . . . .
1.3 Aufbau und Funktionsweise eines Digitalspeicheroszilloskops
1.3.1 Signalerfassung . . . . . . . . . . . . . . . . . . . . .
1.3.2 Triggerung . . . . . . . . . . . . . . . . . . . . . . .
1.3.3 Bedienungsgrundlagen . . . . . . . . . . . . . . . . .
1.3.4 Gedehnte Signaldarstellung . . . . . . . . . . . . . .
1.4 Messmethoden . . . . . . . . . . . . . . . . . . . . . . . . .
1.4.1 yt-Betrieb . . . . . . . . . . . . . . . . . . . . . . . .
1.4.2 xy-Betrieb . . . . . . . . . . . . . . . . . . . . . . .
1.5 Zeigerdiagramme . . . . . . . . . . . . . . . . . . . . . . . .
1.6 Hinweis zur Genauigkeit von Ergebnissen . . . . . . . . . . .
1.7 Serien– und Parallelersatzschaltung . . . . . . . . . . . . . .
1.7.1 Kapazitive Phasenverschiebung . . . . . . . . . . . .
1.7.2 Induktive Phasenverschiebung . . . . . . . . . . . . .
1.7.3 Allgemeines . . . . . . . . . . . . . . . . . . . . . .
1.8 Übungsdurchführung . . . . . . . . . . . . . . . . . . . . . .
1.8.1 Ausmessen einer symmetrischen Rechteckspannung .
1.8.2 Laden und Entladen eines Kondensators . . . . . . . .
1.8.3 R, L und C im Wechselstromkreis . . . . . . . . . . .
1.8.4 RLC–Kombination . . . . . . . . . . . . . . . . . . .
1.8.5 Schaltvorgang an einer RLC–Kombination . . . . . .
1.8.6 Ausmessen einer unbekannten Kombination . . . . . .
1.8.7 Beobachten von nichtlinearem Verhalten . . . . . . .
1.9 Fragen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
9
9
10
10
10
12
13
13
14
15
21
21
21
22
24
24
25
26
28
30
31
31
31
33
34
34
35
35
36
2 Netzwerke und Drehstrom
2.1 Ersatzspannungsquelle . . . . . . . . . . . . .
2.1.1 Theorie . . . . . . . . . . . . . . . . .
2.1.2 Spannungs– und stromrichtiges Messen
2.2 Leistungsanpassung . . . . . . . . . . . . . . .
2.3 Spannungsteiler . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
39
39
39
41
42
43
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
INHALTSVERZEICHNIS
8
2.4
2.5
2.6
2.7
2.8
2.9
2.3.1 Unbelasteter und belasteter Spannungsteiler . . . . . . . .
Frequenzunabhängiger Spannungsteiler . . . . . . . . . . . . . .
2.4.1 Theorie . . . . . . . . . . . . . . . . . . . . . . . . . . .
Drehstrom . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.1 Wechselstromkenngrößen . . . . . . . . . . . . . . . . .
Leistungsmessung bei Sinusgrößen . . . . . . . . . . . . . . . . .
Dreiphasenwechselstrom . . . . . . . . . . . . . . . . . . . . . .
2.7.1 Einführung . . . . . . . . . . . . . . . . . . . . . . . . .
2.7.2 Spannungen und Phasenlage . . . . . . . . . . . . . . . .
2.7.3 Leistungsmessung in Dreileitersystemen - Aronschaltung .
Übungsdurchführung . . . . . . . . . . . . . . . . . . . . . . . .
2.8.1 Leistungsanpassung . . . . . . . . . . . . . . . . . . . .
2.8.2 Spannungsteiler . . . . . . . . . . . . . . . . . . . . . . .
2.8.3 Frequenzkompensierter Spannungsteiler . . . . . . . . . .
2.8.4 Effektivwertmessung . . . . . . . . . . . . . . . . . . . .
2.8.5 Sternschaltung . . . . . . . . . . . . . . . . . . . . . . .
2.8.6 Dreieckschaltung . . . . . . . . . . . . . . . . . . . . . .
Fragen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 Transformator
3.1 Theoretische Grundlagen des Transformators . . . . . .
3.1.1 Idealer Transformator . . . . . . . . . . . . . .
3.1.2 Ersatzschaltbild des realen Transformators . . .
3.2 Übungsdurchführung . . . . . . . . . . . . . . . . . . .
3.2.1 Bestimmen des Transformator–Ersatzschaltbildes
3.2.2 Eigenbau–Trafo . . . . . . . . . . . . . . . . . .
3.3 Fragen . . . . . . . . . . . . . . . . . . . . . . . . . . .
4 Filter und Schwingkreise
4.1 Allgemeines . . . . . . . . . . . . . . . . .
4.1.1 Dämpfungsmaß und Bodediagramm
4.1.2 Bandbreite und Grenzfrequenz . . .
4.2 Filter . . . . . . . . . . . . . . . . . . . . .
4.3 Schwingkreise . . . . . . . . . . . . . . . .
4.3.1 Parallelschwingkreis . . . . . . . .
4.3.2 Serienschwingkreis . . . . . . . . .
4.4 Übungsdurchführung . . . . . . . . . . . .
4.4.1 Tiefpass . . . . . . . . . . . . . . .
4.4.2 Serienschwingkreis . . . . . . . . .
4.4.3 Bandpass . . . . . . . . . . . . . .
4.5 Fragen . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
43
43
43
44
44
46
47
47
49
49
51
51
51
51
51
52
53
53
.
.
.
.
.
.
.
57
57
57
58
63
63
65
66
.
.
.
.
.
.
.
.
.
.
.
.
69
69
69
69
70
71
71
72
72
72
73
73
74
9
Kapitel 1
Oszilloskop
1.1 Allgemeines
Das Oszilloskop (kurz: Oszi) ist eines der wichtigsten Messgeräte in der Elektrotechnik. Es
dient zur Darstellung von elektrischen Signalen (in der Regel zeitabhängige Signale) auf einem
Bildschirm.
Damit lassen sich
• Signalformen bestimmen (z.B. Sinus, Rechteck, Dreieck. . . )
• Impulse vermessen (z.B. wie lange ist ein Impuls, welche Amplitude hat er...)
• Frequenzen ermitteln (z.B. mit welcher Wiederholrate tritt ein Impuls auf).
Es lassen sich aber auch Zusammenhänge zwischen Signalen herstellen:
• Sind zwei Signale synchron? Haben sie die gleiche Frequenz?
• Gibt es eine Zeitverzögerung oder Phasenverschiebung zwischen den Signalen?
• Frequenzgänge vermessen (z.B. Ausgangssignal zu Eingangssignal eines Filters)
Im Gegensatz zu anderen Messgeräten steht bei Oszilloskopen nicht die Genauigkeit der gemessenen Amplituden im Vordergrund. Vielmehr ist die maximal darstellbare Frequenz sowie
die Anzahl der gleichzeitig messbaren Signale (Kanäle) ein Qualitätskriterium.
Als Bildschirm wurde ursprünglich eine Braun’sche Röhre (1897 von Karl Ferdinand Braun
entwickelt) verwendet, moderne Oszilloskope arbeiten hingegen fast ausschließlich digital und
stellen die Signale auf grafischen Displays dar. Um die Funktionsweise zu verdeutlichen wird
sowohl der Aufbau eines analogen Oszis (mit einer Braun’scher Röhre) als auch die Funktionen eines digitalen (Speicher-) Oszis beschrieben. Im Praktikum wird ein digitales Oszilloskop
verwendet (Tektronix TDS 1002).
KAPITEL 1. OSZILLOSKOP
10
1.2 Aufbau und Funktionsweise eines analogen Oszilloskops
1.2.1 Elektronenstrahlröhre
Eine Oszilloskopröhre besteht aus dem Elektronenstrahlerzeugungssystem, den Ablenksystemen in horizontaler (x) und vertikaler (y) Richtung und dem Leuchtschirm. Abbildung 1.1 zeigt
die Anordnung dieser Komponenten in einem evakuierten Glaskolben.
Abbildung 1.1: Aufbau einer Oszilloskopröhre
Die geheizte Kathode emittiert Elektronen. Diese werden durch die Anode beschleunigt und
durch diverse Elektroden auf dem Leuchtschirm fokussiert, wo sie Leuchterscheinungen hervorrufen. Die Ablenkung des Strahls wird durch ein elektrisches Feld bewerkstelligt. Zu diesem
Zweck sind zwei Plattenpaare, je eines für die x- und die y-Ablenkung, vorgesehen. Im Normalbetrieb wird an die y-Platten eine Spannung angelegt, welche der zu messenden Spannung
proportional ist, und an die x-Platten eine Spannung, welche der Zeit proportional ist (lineare
Rampe).
1.2.2 Blockschaltbild
Abbildung 1.2 zeigt die wichtigsten Komponenten eines Zweikanaloszilloskops mit den Eingängen y1 (CH1) und y2 (CH2) sowie einem externen Triggereingang (EXT. TRIG.).
Die Funktionen der einzelnen Baugruppen sind:
• Eingangswahlschalter: Er erlaubt die Erdung (GND) der Eingangsstufe um die Nulllinie am Schirm einstellen zu können, die direkte Kopplung des Messsignales (DC ... Direct
Current, Gleichstrom) und die Kopplung über einen Kondensator (AC ... Alternating Current,
Wechselstrom). Letztere Möglichkeit wird bei der Messung von Wechselsignalen, welchen ein Gleichspannungsanteil überlagert ist, verwendet. Dadurch bleibt der Gleichanteil
bei der Anzeige unberücksichtigt und es können auch sehr kleine Wechselanteile gemessen werden. Allerdings kommt es bei niederfrequenten Signalen zu einer Verfälschung
der Kurvenform.
1.2. AUFBAU UND FUNKTIONSWEISE EINES ANALOGEN OSZILLOSKOPS
11
Abbildung 1.2: Blockschaltbild eines Zweikanaloszilloskops
• Bereichsumschalter: Er dient der Anpassung des Eingangssignals an den Eingang des
Oszilloskops. Ein grober stufiger Abschwächer ist in Spannung pro Rastereinheit kalibriert, ein fein einstellbarer Verstärker oder Abschwächer erlaubt die stufenlose Skalierung der Anzeige. Allerdings ist bei Verwendung dieser Feineinstellung (VAR) die Kalibrierung der Eingangsempfindlichkeit nicht gegeben (UNCAL).
• Vertikalverstärker und Horizontalverstärker: Um die für die Ablenkung des Elektronenstrahls nötigen hohen Spannungen zu erreichen sind geeignete Verstärkerstufen vorgesehen.
• Kanalumschalter: Der Benutzer kann auswählen, welches der beiden Eingangssignale
er am Bildschirm betrachten will. Da für die Vertikalablenkung nur ein Plattenpaar vorgesehen ist, muss zwischen den beiden Kanälen umgeschaltet werden. Um dennoch beide
Kurven gleichzeitig am Schirm anzuzeigen gibt es zwei Möglichkeiten: Bei der ersten
Variante werden die beiden Signale abwechselnd (ALTernating) dargestellt. Durch das
Nachleuchten des Bildschirms entsteht für den Betrachter ein Bild mit zwei unabhängigen
Signalverläufen. Sind die Signalfrequenzen sehr niedrig kommt es jedoch zu Flimmereffekten. Die andere Möglichkeit ist während eines Strahldurchlaufs permanent zwischen
den beiden Signalen hin und herzuschalten, wodurch die Signale in kurze Stücke "‘zerhackt"’ (CHOPped) werden. Diese Methode eigent sich gut für langsame Signale. Weiters
kann man die Signale beider Kanäle addieren (y1 +y2 ) oder durch zusätzliches Invertieren
eines Kanals subtrahieren (y1 − y2 ).
• Triggereinheit: Sie dient der zeitlichen Abstimmung der Zeitablenkung mit dem Messsignal. Es kann auf y1 (CH1 ... Channel 1), y2 (CH2 ... Channel 2) oder auf ein anderes
Signal (EXT ... Extern) getriggert werden. Bei der Triggerung auf die steigende Flanke
(↑) wird bei jedem Überschreiten des Triggerpegels ein Triggerimpuls erzeugt, bei der
Triggerung auf die fallende Flanke (↓) bei jedem Unterschreiten. Die Höhe des Triggerpegels kann eingestellt werden (LEVEL). Bei normaler Triggerung (NORM) bleibt
der Schirm beim Ausbleiben von Triggerimpulsen finster, bei automatischer Triggerung
KAPITEL 1. OSZILLOSKOP
12
(AUTO) läuft der Zeitablenkgenerator in diesem Fall frei und erzeugt ein durchlaufendes
Bild.
• Zeilenablenkgenerator: Um den Elektronenstrahl in horizontaler Richtung zu bewegen,
muss eine mit der Zeit linear ansteigende Spannung generiert werden. Beim Auftreten
eines Triggerimpulses startet der Zeilenablenkgenerator einen Durchlauf einer Sägezahnspannung mit einstellbarer Anstiegszeit (Zeitbasis kalibriert in Zeit pro Rastereinheit).
Dadurch bewegt sich der Strahl mit konstanter Geschwindigkeit von links nach rechts
und sehr schnell wieder zurück.
• Dunkeltastung: Um den Strahl beim Rücklauf und beim Warten auf ein neues Triggerereignis unsichtbar zu machen, wird eine negative Spannung an den Wehneltzylinder des
Strahlerzeugungssystems (Z-Modulation) gelegt. Dadurch wird der Elektronenstrahl abgeschaltet (dunkelgetastet).
1.2.3 Triggerung
Das Zusammenspiel von Trigger und Zeitablenkung zeigen die Diagramme in Abbildung 1.3.
In diesem Beispiel sei die Triggerung auf die positive Flanke gewählt. Befindet sich der Strahl
dunkelgetastet in Warteposition, so wird beim Auftreten eines Triggerimpulses der Sägezahn
der Zeitablenkung gestartet und der Strahl hellgetastet. Triggerereignisse, die während eines
Strahldurchlaufs stattfinden, werden ignoriert. Nach einem vollständigen Durchlauf wird der
Strahl dunkelgetastet und wieder in die Anfangsposition gebracht. Bei periodischer Wiederholung dieses Vorgangs ergibt sich ein stehendes Schirmbild. Das analoge Oszilloskop ist daher
nur für die Betrachtung periodischer Signale geeignet.
Abbildung 1.3: Zeitdiagramme von Messsignal, Trigger, Zeitablenkung und Dunkeltastung sowie resultierendes Schirmbild
1.3. AUFBAU UND FUNKTIONSWEISE EINES DIGITALSPEICHEROSZILLOSKOPS 13
1.3 Aufbau und Funktionsweise eines Digitalspeicheroszilloskops
1.3.1 Signalerfassung
Die Funktionsweise eines digitalen Speicheroszilloskops (DSO) unterscheidet sich grundlegend
von der eines analogen Oszis. Die Eingangssignale werden von Analog-Digital-Wandlern digitalisiert, anschließend gespeichert und auf einem LCD-Display als Kurvenzug angezeigt. Im
Erfassungsmodus ist festgelegt, auf welche Weise das Signal digitalisiert wird. Die Einstellung
der Zeitbasis beeinflusst die Zeitdauer und Detailgenauigkeit der Erfassung.
Erfassungsmodi
Es gibt drei Erfassungsmodi: Sample (Abtasten), Pk Detect (Spitzenwert) und Mittelwert.
Abtasten (Sample) : Bei diesem Erfassungsmodus wird das Signal vom Oszilloskop in regelmäßigen Zeitabständen abgetastet und als Kurvenzug dargestellt. In diesem Modus
werden Signale meistens sehr präzise wiedergegeben, es werden jedoch keine schnellen
Signalschwankungen erfasst, die zwischen den einzelnen Abtastungen auftreten können.
Dies kann zu Aliasing führen, so dass schmale Impulse möglicherweise nicht erkannt
werden. In diesem Fall sollten Sie den Spitzenwerterfassungsmodus zur Erfassung der
Daten verwenden.
Spitzenwerterfassung: Bei diesem Erfassungsmodus zeichnet das Oszilloskop die höchsten
und niedrigsten Werte des Eingangssignals in jedem Abtastintervall auf und stellt sie
als Kurvenzug dar. Auf diese Weise kann das Oszilloskop schmale Impulse erfassen und
anzeigen, die im Abtastmodus womöglich gar nicht entdeckt worden wären. Störrauschen
tritt in diesem Modus stärker in Erscheinung.
Mittelwert: In diesem Modus erfasst das Oszilloskop mehrere Perioden eines Signals, bildet
daraus eine Mittelwertkurve und zeigt diese an. Dadurch lässt sich unkorreliertes Rauschen reduzieren.
Zeitbasis
Das Oszilloskop digitalisiert Signale, indem es den Wert eines Eingangssignals an einzelnen
Punkten erfasst. Anhand der Zeitbasis lässt sich festlegen, wie oft die Werte digitalisiert werden.
Zur Einstellung der Zeitbasis auf eine für Ihre Zwecke geeignete Horizontalskala verwenden Sie
den Drehknopf SEC/DIV.
Zeitbereichs-Aliasing
Aliasing tritt dann auf, wenn das Oszilloskop das Signal nicht schnell genug abtastet, um eine
genaue Signalaufzeichnung darzustellen. In diesem Fall zeigt das Oszilloskop ein Signal mit einer niedrigeren Frequenz an als das tatsächliche Eingangssignal oder stellt trotz Triggerung ein
instabiles Signal dar. Der Aliasing–Effekt ist in Abbildung 1.4 dargestellt. Zur Vermeidung von
Aliasing muss das Oszilloskop das Signal mehr als doppelt so schnell abtasten wie die höchste
Frequenzkomponente des Signals. Die höchste Frequenz, welche bei gegebener Oszilloskop–
Abtastrate theoretisch dargestellt werden kann, wird als Nyquist-Frequenz bezeichnet. Die Abtastrate wird als Nyquist–Rate bezeichnet und beträgt das Doppelte der Nyquist–Frequenz.
KAPITEL 1. OSZILLOSKOP
14
Abbildung 1.4: Aliasing durch Unterabtastung
1.3.2 Triggerung
Einer der wichtigsten Unterschiede zwischen analogem und digitalem Oszi ist die Triggerung.
Beim analogen Oszi kann nur betrachtet werden, was nach einem Triggerereignis passiert (da
der Strahl ja immer mit dem Trigger startet). Digitale Oszilloskope können auch Signalverläufe
vor einem Trigger (pre–trigger) darstellen, indem während dem Warten auf das Triggerereignis
die Signale laufend gespeichert werden. Erst nach dem Auftreten des Triggerereignisses wird
die Kurvenform angezeigt.
Ein weiterer Vorteil digitaler Oszilloskope ist, dass auch nicht periodische Signale betrachtet
werden können. Ein einmal gespeichertes Signal kann beliebig lange auf dem Bildschirm dargestellt werden. Dazu wird die folgende Sequenz nur einmal durchlaufen (SINGLE SEQ), im
RUN–Modus wird die Sequenz endlos wiederholt, das Oszi arbeitet vergleichbar einem analogen Gerät.
1. Es werden genügend Daten erfasst, um den Teil der Signalaufzeichnung links vom Triggerpunkt auszufüllen. Dies wird auch als Vortrigger bezeichnet.
2. Es werden fortlaufend Daten erfasst, während das Oszilloskop auf das Auftreten der Triggerbedingung wartet.
3. Die Triggerbedingung wird erkannt.
4. Es werden weiterhin Daten erfasst, bis die Signalaufzeichnung abgeschlossen ist.
5. Das neu erfasste Signal wird angezeigt.
Quelle
Die Option Trigger–Quelle wird benutzt, um das Signal auszuwählen, welches das Oszilloskop
als Trigger verwendet. Die Quelle kann ein beliebiges Signal sein, das über den Kanal-BNCStecker oder über den EXT TRIG–BNC–Stecker eingespeist wird. Der Trigger kann auch von
der Netzversorgung abgeleitet werden (nur bei Flankentriggern verfügbar).
Arten
Das Oszilloskop verfügt über drei Trigger-Arten: Flanke, Video und Impulsbreite.
1.3. AUFBAU UND FUNKTIONSWEISE EINES DIGITALSPEICHEROSZILLOSKOPS 15
Modi
Sie können einen Trigger–Modus auswählen, um festzulegen, wie das Oszilloskop Daten erfassen soll, wenn es keine Triggerbedingung erkennt. Im Normal–Modus wird nur bei einem
realen Triggerereignis die Triggerung ausgelöst, das aufgenommene Signal wird bis zum nächsten Triggerereignis am Bildschirm angezeigt. Im Auto–Modus wird auch ein Trigger ausgelöst,
wenn eine gewisse Zeit kein Triggerereignis stattfand. Dadurch bleibt ein einmal aufgezeichnetes Signal nicht beliebig lange am Bildschirm und der Benutzer kann erkennen, dass kein
Triggerereignis mehr auftritt.
Kopplung
Mit der Option Trigger–Kopplung können Sie bestimmen, welcher Signalteil zur Triggerschaltung geleitet werden soll. Auf diese Weise läßt sich das Signal stabiler anzeigen. Zur Verwendung der Trigger–Kopplung drücken Sie die Taste TRIG MENÜ und wählen einen Flanken–
oder Impulstrigger sowie eine Kopplungsoption aus. Um das konditionierte Signal anzuzeigen,
das zur Triggerschaltung geleitet wird, halten Sie die Taste TRIG VIEW gedrückt.
Position
Durch Einstellung der horizontalen Position wird die Zeit zwischen dem Trigger und der Bildschirmmitte festgesetzt.
Flanke und Pegel
Die Bedienelemente Flanke und Pegel helfen bei der Trigger–Definition. Mit der Option Flanke
(nur bei Flankentriggern verfügbar) wird festgelegt, ob der Triggerpunkt auf der steigenden oder
abfallenden Flanke liegen soll. Über den Drehknopf TRIGGERPEGEL wird eingestellt, wo der
Triggerpunkt auf der Flanke erscheint.
1.3.3 Bedienungsgrundlagen
Die Front des TDS 1002 ist in der Abbildung 1.5 dargestellt.
Anzeigebereich
Zusätzlich zur Anzeige des Signals selbst enthält der Anzeigebereich eine Fülle von Details
über das Signal sowie die Oszilloskopeinstellungen. In Abbildung 1.6 bedeuten die Zahlen folgendes:
1: Das angezeigte Symbol steht für den Erfassungsmodus: Abtastmodus, Spitzenwertmodus
und Mittelwertmodus.
2: Der Triggerstatus weist auf folgendes hin:
• Armed: Das Oszilloskop erfasst Vortrigger-Daten. In diesem Zustand werden sämtliche Trigger ignoriert.
KAPITEL 1. OSZILLOSKOP
16
Abbildung 1.5: Front des TDS 1002
• Ready: Alle Vortrigger–Daten wurden erfasst, das Oszilloskop ist jetzt zur Trigger–
Erkennung bereit.
• Triggered: Das Oszilloskop hat einen Trigger erkannt und erfasst jetzt die Nachtrigger–
Daten.
• Stop: Das Oszilloskop hat die Erfassung der Signaldaten beendet.
• Acquisition complete: Das Oszilloskop hat eine Einzelfolgeerfassung abgeschlossen.
• Scan: Signaldaten werden im Abtastmodus vom Oszilloskop kontinuierlich erfasst
und angezeigt.
3: Der Marker zeigt die horizontale Triggerposition an. Drehen Sie den Knopf HORIZONTAL
POSITION, um die Position des Markers einzustellen.
4: Die Anzeige zeigt die Zeit in der Rastermitte bezogen auf die horizontale Triggerposition
an. Die Triggerzeit ist Null.
5: Der Marker zeigt den Flanken- oder Impulsbreitentriggerpegel an.
6: Bildschirmmarkierungen zeigen die erdbezogenen Messpunkte der angezeigten Signale. Falls
keine Markierung vorliegt, wird der Kanal nicht angezeigt.
7: Ein Pfeilsymbol weist darauf hin, dass das Signal invertiert wird.
8: Die vertikalen Skalenfaktoren der Kanäle werden angezeigt.
9: Das BW–Symbol deutet darauf hin, daß die Bandbreite dieses Kanals begrenzt wurde.
10: Anzeige zeigt die Einstellung der Hauptzeitbasis (Main Time Base) an.
11: Anzeige zeigt die Fenstereinstellung der Zeitbasis an, wenn diese verwendet wird.
1.3. AUFBAU UND FUNKTIONSWEISE EINES DIGITALSPEICHEROSZILLOSKOPS 17
Abbildung 1.6: Schirmbild des TDS 1002
12: Anzeige zeigt die zur Triggerung verwendete Triggerquelle an.
13: Das Symbol steht für die jeweils ausgewählte Trigger-Art:
Flankentrigger auf der steigenden Flanke
Flankentrigger auf der fallenden Flanke
Videotrigger auf der Zeilensynchronisation
Videotrigger auf der Halbbildsynchronisation
Impulsbreiten-Trigger, positive Polarität
Impulsbreiten-Trigger, negative Polarität
14: Die Anzeige zeigt den Flanken- oder Impulsbreitentriggerpegel an.
15 : Im Anzeigebereich erscheinen Meldungen, die Ihnen weiterhelfen sollen. Manche werden
allerdings nur drei Sekunden lang angezeigt. Wenn Sie ein gespeichertes Signal abrufen,
werden Informationen zum Referenzsignal angezeigt, z.B. RefA 1,00 V 50 µs.
16: Anzeige zeigt die Triggerfrequenz an.
Vertikale Bedienelemente
Im Folgenden sind die Bedienelemente nach Abbildung 1.7 erklärt.
CH 1, CH 2, CURSOR 1 und CURSOR 2 POSITION: Positioniert das Signal vertikal. Wenn
Sie Cursor anzeigen und verwenden, leuchtet die LED, um auf die alternative Funktion
der Drehknöpfe zum Verschieben der Cursor hinzuweisen.
CH 1, CH 2 MENÜ: Zeigt die Auswahl im vertikalen Menü an und schaltet die Anzeige des
Kanalsignals ein und aus.
KAPITEL 1. OSZILLOSKOP
18
Abbildung 1.7: Bedienelemente für die Vertikalablenkung
VOLTS/DIV (CH 1, CH 2): Dient zur Auswahl der kalibrierten Skalenfaktoren.
MENÜ MATH: Ruft das Menü für mathematische Signaloperationen auf und lässt sich zum
Ein- und Ausschalten des berechneten Signals verwenden.
Horizontale Bedienelemente
Im Folgenden sind die Bedienelemente nach Abbildung 1.8 erklärt.
Abbildung 1.8: Bedienelemente für die Zeitablenkung
POSITION: Dient zur Einstellung der horizontalen Position aller Kanäle und berechneten Signale. Die Auflösung dieses Drehknopfes variiert je nach Zeitbasis-Einstellung.
MENÜ HORIZ: Ruft das horizontale Menü auf.
AUF NULL SETZEN: Setzt die Horizontalposition auf Null.
1.3. AUFBAU UND FUNKTIONSWEISE EINES DIGITALSPEICHEROSZILLOSKOPS 19
SEC/DIV: Dient zur Auswahl der horizontalen Zeit/div (Skalenfaktor) für die Haupt- oder
Fensterzeitbasis. Wenn der Zoombereich aktiviert ist, wird die Breite des Zoombereichs
durch Änderung der Fensterzeitbasis geändert.
Trigger-Steuerung
Für die Einstellung des Triggers sind die Bedienelemente von Abbildung 1.9 notwendig.
Abbildung 1.9: Bedienelemente für die Trigger-Steuerung
PEGEL und ERWEITERT: Bei Verwendung eines Flankentriggers besteht die Hauptfunktion des Drehknopfes PEGEL darin, die Amplitude einzustellen, die das Signal zum Auslösen einer Erfassung durchlaufen muss. Außerdem wird der Drehknopf ERWEITERT
zur Durchführung erweiterter Alternativfunktionen verwendet. Die LED unter dem Drehknopf leuchtet, wenn eine alternative Funktion aktiviert ist.
MENÜ TRIG: Ruft das Trigger-Menü auf.
AUF 50 % SETZEN: Der Triggerpegel wird auf den vertikalen Mittelpunkt zwischen den
Spitzenwerten des Triggersignals gesetzt.
TRIG ZWANG: Schließt die Erfassung ab, ganz gleich ob ein adäquates Triggersignal vorliegt oder nicht. Wenn die Erfassung bereits angehalten wurde, hat diese Taste keinerlei
Auswirkungen.
TRIG ANZEIGE: Wenn Sie die Taste TRIG ANZEIGE gedrückt halten, wird statt des Kanalsignals das Triggersignal angezeigt. So können Sie beispielsweise feststellen, wie sich
die Triggereinstellungen z.B. bei Triggerkopplung auf das Triggersignal auswirken.
KAPITEL 1. OSZILLOSKOP
20
Menü- und Steuerungstasten
Abbildung 1.10 zeigt die Tasten zum Aufrufen der Menüs und zur Steuerung der Oszilloskopfunktionen.
Abbildung 1.10: Bedienelemente für die Trigger-Steuerung
SPEICHERN/ABRUFEN: Ruft das Menü Speichern/Abrufen für Einstellungen und Signale
auf.
MESSUNG: Ruft das Menü für automatische Messungen auf.
ERFASSUNG: Ruft das Menü Erfassung auf.
DISPLAY: Ruft das Menü Display auf.
CURSOR: Ruft das Menü Cursor auf. Über die Drehknöpfe für die vertikale Position läßt sich
die Cursorposition einstellen, während das Cursor-Menü angezeigt wird und die Cursor
aktiviert werden. Die Cursor werden auch nach Verlassen des Cursor-Menüs angezeigt
(es sei denn, die Cursor-Option wurde auf AUS gestellt), lassen sich aber nicht einstellen.
DIENSTPGM: Ruft das Menü Dienstprogramm auf.
HILFE: Ruft das Menü Hilfe auf.
GRUNDEINSTELLUNG: Ruft die werkseitige Einstellung ab.
AUTO-SETUP: Das Oszilloskop wird automatisch so eingestellt, dass eine verwertbare Anzeige der Eingangssignale stattfindet.
EINZELFOLGE: Das Oszilloskop erfasst eine Einzelfolge und hält dann an.
RUN/STOP: Das Oszilloskop erfasst Signaldaten kontinuierlich oder hält die Erfassung an.
DRUCKEN: Startet Druckvorgänge. Zum Drucken ist das Erweiterungsmodul mit Centronics" , RS-232- oder GPIB-Schnittstelle erforderlich.
Anschlüsse
Die Anschlüsse des Oszilloskops sind in Abbildung 1.11 dargestellt.
TASTKOPF ABGL: Ausgang und Erdung für die Spannungstastkopfkompensation. Wird verwendet, um den Tastkopf mit der Eingangsschaltung des Oszilloskops abzugleichen. Die
Erdung für die Tastkopfkompensation und die Abschirmung der BNC-Stecker sind mit
der Stromnetzerdung verbunden und fungieren als Erdungsklemmen.
1.4. MESSMETHODEN
21
Abbildung 1.11: Anschlussbuchsen
CH 1, CH 2: Eingangsstecker zur Anzeige von Signalen.
EXT TRIG: Eingangsstecker für eine externe Triggerquelle. Verwenden Sie das Trigger-Menü,
um die Triggerquelle Ext. oder Ext./5 auszuwählen.
VORSICHT: Wenn Sie eine Spannungsquelle an eine Erdungsklemme oder den Außenleiter einer BNC-Buchse (Koaxialstecker) anschließen, kann das Oszilloskop oder der
Prüfaufbau beschädigt werden. Schließen Sie daher keinesfalls eine Spannungsquelle an
eine Erdungsklemme oder den Außenleiter einer BNC-Buchse an!
1.3.4 Gedehnte Signaldarstellung
Bei einem analogen Oszilloskop kann ein Signaldetail, welches eine bestimmte Zeit nach dem
Triggerzeitpunkt auftritt, durch eine verzögerte Zeitbasis gedehnt dargestellt werden. Dabei
wird zuerst die Verzögerungszeit (= Zeit zwischen Triggerzeitpunkt und interessantem Signaldetail) gesucht (Search) und eingestellt (Delay). Die Darstellung am Schirm beginnt dann erst
verzögert zum eingestellten Zeitpunkt. Jetzt kann die Zeitablenkung gedehnt werden, um das
gewünschte Detail in einer höheren Zeitauflösung darzustellen.
Beim Digitaloszilloskop wird diese Betriebsart im Horizontalmenü eingestellt und funktioniert,
obwohl digital realisiert, ähnlich. Ein großer Vorteil des Digitaloszilloskops ist der Pretrigger.
Da die Digitalisierung ständig läuft und bei Auftreten eines Triggerereignisses nach einer gewissen Zeit gestoppt wird, befinden sich auch Daten für die Zeit vor dem Triggerereignis im Speicher. Die Zeitverschiebung zwischen Triggerzeitpunkt und darzustellendem Signalausschnitt
kann daher auch negativ eingestellt werden.
1.4 Messmethoden
1.4.1 yt-Betrieb
Kalibrierte Messung
Im Normalbetrieb (yt-Betrieb) können die Zeitverläufe von ein oder zwei Signalen dargestellt und ausgemessen werden. Für Messungen müssen die entsprechenden Rastereinheiten am
Schirm abgelesen und mit der eingestellten Eingangsempfindlichkeit beziehungsweise Zeitablenkung multipliziert werden. In diesem Fall müssen die Knöpfe für die variablen Einstellungen auf 1 bzw. CAL gestellt werden. In den folgenden Formeln bedeutet „Div“ Rastereinheit
(engl. „Division“).
U
U Skalen f aktor
=
·
(1.1)
V Div
V/Div
KAPITEL 1. OSZILLOSKOP
22
t
t Skalen f aktor
=
·
s Div
s/Div
(1.2)
Verhältnismessung
Die variablen Abbildungsmaßstäbe bei Eingangsempfindlichkeit und Zeitablenkung werden für
Verhältnismessungen benötigt.
Messung von Anstiegs- und Abfallzeit: Die Anstiegszeit eines Impulses ist definiert durch
jene Zeit, in welcher das Signal von 10 % auf 90 % des Gesamthubes ansteigt. Das Oszilloskop
ermöglicht auch im Menü Messung die selbständige Messung von Anstiegs- und Abfallzeit.
Phasenmessung: Zur Messung der Phasenverschiebung zwischen zwei Wechselgrößen gleicher Frequenz betrachtet man gleichwertige Punkte der beiden Größen. Am einfachsten misst
man die Nulldurchgänge.
Am Analogoszilloskop wird durch Dehnung und Positionierung der Referenzkurve eine vollständige Periode τ auf eine ganze Zahl von Rastereinheiten (z. B. 8) eingestellt. Der Abstand
eines Nulldurchganges des Referenzsignales zu jenem des zweiten Signales ergibt die Phasenverschiebung nach folgender Formel:
ϕ
ϕ
Div
= τ · 360
Grad
Div
(1.3)
Am Speicheroszilloskop verwendet man die Zeit-Cursor. Zuerst stellt man beide Cursor auf aufeinanderfolgende Nulldurchgänge und misst mit Delta die Periodendauer τ. Danach stellt man
den zweiten Cursor auf den Nulldurchgang das zweiten Signales und misst die Zeit t zwischen
den Nulldurchgängen des ersten und des zweiten Signales. Die Phasenverschiebung ist dann
t
ϕ
= · 360
Grad τ
(1.4)
Das Vorzeichen der Phasenverschiebung ergibt sich je nach Vor- oder Nacheilung nach folgender Regel: Tritt der Nulldurchgang des zu messenden Signales nach dem (d. h. rechts vom)
Nulldurchgang des Referenzsignales auf, so ist die Phase negativ. Bei voreilendem Signal ist
die Phase positiv (siehe auch Kapitel 1.7).
1.4.2 xy-Betrieb
Anstatt die Zeitablenkung zu verwenden, kann auch ein Messsignal an die x-Ablenkung angeschlossen werden. In Verbindung mit einem zweiten Signal an der y-Ablenkung ergibt sich bei
der Messung sinusförmiger Größen eine geschlossene Kurve als Schirmbild.
Die Umschaltung zwischen xt- und xy-Betrieb geschieht am TDS 1002 im Menü DISPLAY.
ACHTUNG: Sind im xy-Betrieb keine Signale vorhanden, so ist am Schirm nur ein Punkt zu
sehen. Bei einem Analogoszilloskop mit Kathodenstrahlröhre kommt es dadurch bei normaler
Einstellung der Strahlintensität durch die Konzentration des Elektronenstrahles auf eine Stelle
zur Zerstörung des Leuchtschirmes! Sollen die Positionen von x- und y-Signal bei der Stellung
„GND“ des Eingangswahlschalters zentriert werden, so muss die Strahlintensität (INTENSITY)
verringert werden.
1.4. MESSMETHODEN
23
Signale gleicher Frequenz
Die Phasenverschiebung lässt sich mit der Ellipsenmethode folgendermaßen bestimmen:
1. Erste Spannung U1 · sin(ωt) an den x-Eingang legen;
2. Zweite Spannung U2 · sin(ωt + ϕ) an den y-Eingang legen;
3. Ellipse zentrieren;
4. Zur Messung yx=0 und ymax oder xy=0 und xmax ablesen und Phasenverschiebung nach
(1.5) berechnen.
sin(ϕ) =
yx=0 xy=0
=
ymax
xmax
(1.5)
In den Sonderfällen ϕ = 0◦ und ϕ = 180◦ entartet die Ellipse zu einer Geraden. Dies ermöglicht
eine einfache Prüfung auf Phasengleichheit.
Für voreilendes y erfolgt der Strahlumlauf im Uhrzeigersinn, für nacheilendes y entgegengesetzt. Aus dem Schirmbild ist dies aber wegen der Augenträgheit nicht erkennbar, sodass die
Ellipse keine Auskunft über das Vorzeichen des Phasenwinkels gibt.
0
I
0
ï1
ï1
I
e = //4
1
0
U
e = //2
ï1
ï1
1
1
1
0
0
ï1
ï1
I
I
e=0
1
0
U
1
ï1
ï1
0
U
e = 3/4 /
1
0
U
1
Abbildung 1.12: xy-Diagramme für unterschiedliche Phasenverschiebungen
Lissajous-Figuren
Sind die Frequenzen von x- und y-Signal ( fx und fy ) verschieden, so ergibt sich im allgemeinen
f
kein stehendes Schirmbild. Nur wenn das Verhältnis fyx rational ist, ergibt sich eine so genannte
Lissajous-Figur (Abbildung 1.13).
KAPITEL 1. OSZILLOSKOP
24
Abbildung 1.13: Lissajous-Figur für
fy
fx
=
3
2
Das Frequenzverhältnis lässt sich aus dem Schirmbild bestimmen. Man zählt die Anzahl der
Maxima in x-Richtung (nx , d. h. Stellen mit größtmöglicher x-Auslenkung) und in y-Richtung
(ny ) und setzt sie laut Gleichung (1.6) ins Verhältnis.
f y ny
=
f x nx
(1.6)
1.5 Zeigerdiagramme
Mit Zeigerdiagrammen lassen sich die Phasenlage von Strom und Spannung oder die Admittanz
/Impedanz einer Schaltung darstellen. Im Strom-/Spannungsdiagramm werden die Amplitude
und die Phasenlage von Strom und Spannung durch Zeiger visualisiert. Wichtig ist, dass die
Phasendifferenz zwischen Spannung und Strom aus dem Diagramm abgelesen werden kann.
Deshalb müssen x- und y-Achse die gleiche Skalierung aufweisen. Diese sollte in einer Art
Legende neben dem Diagramm für Strom und Spannung angegeben werden (Bsp: 1cm =
ˆ 1V,
1cm =
ˆ 2mA). Die Beschriftung der Achsen mit der Skalierung ist nicht sinnvoll, da es schwierig ist, eine Achse mit 2 unterschiedlichen Skalierungen zu beschriften ohne Übersichtlichkeit/Lesbarkeit zu verlieren. In der Regel wird die Phasenlage so gewählt, dass einer der Zeiger
auf der x-Achse liegt (Beispiel: siehe Abbildung 1.14).
Mit einem Impedanz-/Admittanzdiagramm werden Betrag und Phase der Impedanz/Admittanz
dargestellt. Auch hier ist es wichtig, dass die Phase direkt aus dem Diagramm abgelesen werden
kann. Somit müssen reelle und imaginäre Achse die gleiche Skalierung aufweisen (Beispiel:
siehe Abbildung 1.15).
1.6 Hinweis zur Genauigkeit von Ergebnissen
Die Genauigkeit einer Messung muss sich auch in Endergebnissen und Rechnungen widerspiegeln. Misst man beispielsweise an einem Widerstand einen Spannungsabfall von 3.7 V, wobei
die Spannung auf 0.1 V genau abgelesen werden kann und einen Strom von 10 mA (± 1 mA),
so ist es nicht sinnvoll den Widerstand mit mehr als zwei signifikaten Stellen anzugeben (R =
0.37 kΩ).
Mehr Informationen zu dem Thema finden sie beispielsweise unter http://www.physik.uniwuerzburg.de/˜reusch/fehler/wisem0102/vorlesung1.pdf
1.7. SERIEN– UND PARALLELERSATZSCHALTUNG
25
Im
U : 1cm =
ˆ 1V
I: 1cm =
ˆ 2mA
U
∆ϕ
I
Re
Abbildung 1.14: Beispiel für ein Strom-/Spannungsdiagramm
1.7 Serien– und Parallelersatzschaltung
Aus einer Strom–/Spannungsmessung an einem Zweipol geht nicht hervor, ob die Impedanz
Z aus in Serie geschalteten oder parallelgeschalteten Elementen besteht. Z lässt sich folgendermaßen als Serienschaltung eines Wirkwiderstandes (ohmschen Widerstandes) R und eines
Blindwiderstandes X darstellen:
Z=
U
U
cos(ϕZ ) + j sin(ϕZ ) = R + jX
I
I
(1.7)
Für die Parallelersatzschaltung ergibt sich die duale Formel für die Admittanz Y als Summe von
Wirkleitwert G und Blindleitwert B:
Y=
I
I
cos(ϕY ) + j sin(ϕY ) = G + jB
U
U
(1.8)
Beim Vorzeichen des Blindanteiles ist zu beachten, dass die Phasenverschiebung ϕ auf die richtige Größe bezogen wird. Die Impedanz errechnet sich aus Spannung durch Strom, daher wird
als ϕZ die Phasenverschiebung der Spannung gegen den Strom bezeichnet:
ϕZ = ϕU − ϕI
(1.9)
Bei der Admittanz (Strom durch Spannung) gilt:
ϕY = ϕI − ϕU
(1.10)
Je nach Vorzeichen ist eine Induktivität L oder eine Kapazität C als Realisierung von X bzw. B
zu wählen.
KAPITEL 1. OSZILLOSKOP
26
140
Im(Z)in Ω
120
100
80
60
40
20
0
∆ϕ
0 20 40 60 80
Re(Z) in Ω
Abbildung 1.15: Beispiel für ein Impedanzdiagrammm
1.7.1 Kapazitive Phasenverschiebung
Kapazitive Phasenverschiebung heißt, dass die Spannung dem Strom nacheilt. Wegen Ũ = Z I˜
ist ϕZ < 0, beziehungsweise wegen I˜ = Y Ũ ist ϕY > 0.
Parallelschaltung
Abbildung 1.16: Schaltung und Zeigerdiagramme für Admittanz und Strom bzw. Spannung
einer Parallelschaltung von Widerstand und Kondensator
1
+ jωC
R
#
"
1
+ jωC Ũ
I˜ =
R
Y=
u(t) = Û sin(ωt) ,
ϕu = 0
i(t) = Iˆ sin(ωt + ϕi ) ,
ϕi > 0
(1.11)
(1.12)
(1.13)
1.7. SERIEN– UND PARALLELERSATZSCHALTUNG
27
Abbildung 1.17: Zeitdiagramm von Strom und Spannung bei der Parallelschaltung von Widerstand und Kondensator
Serienschaltung
Abbildung 1.18: Schaltung und Zeigerdiagramme für Impedanz und Strom bzw. Spannung einer
Serienschaltung von Widerstand und Kondensator
1
jωC
"
#
j
Ũ = R −
I˜
ωC
(1.14)
Z = R+
(1.15)
Abbildung 1.19: Zeitdiagramm von Strom und Spannung bei der Serienschaltung von Widerstand und Kondensator
i(t) = Iˆ sin(ωt) ,
ϕi = 0
u(t) = Û sin(ωt + ϕu ) ,
ϕu < 0
(1.16)
KAPITEL 1. OSZILLOSKOP
28
1.7.2 Induktive Phasenverschiebung
Induktive Phasenverschiebung heißt, dass der Strom der Spannung nacheilt. Wegen I˜ = Y Ũ ist
ϕY < 0, beziehungsweise wegen Ũ = Z I˜ ist ϕZ > 0.
Parallelschaltung
Abbildung 1.20: Schaltung und Zeigerdiagramme für Admittanz und Strom bzw. Spannung
einer Parallelschaltung von Widerstand und Spule
1
1
+
R jωL
"
#
1
j
−
Ũ
I˜ =
R ωL
Y=
(1.17)
(1.18)
Abbildung 1.21: Zeitdiagramm von Strom und Spannung bei der Parallelschaltung von Widerstand und Induktivität
u(t) = Û sin(ωt) ,
ϕu = 0
ϕi < 0
i(t) = Iˆ sin(ωt + ϕi ) ,
(1.19)
1.7. SERIEN– UND PARALLELERSATZSCHALTUNG
29
Serienschaltung
Abbildung 1.22: Schaltung und Zeigerdiagramme für Impedanz und Strom bzw. Spannung einer
Serienschaltung von Widerstand und Spule
Z = R + jωL
(1.20)
Ũ = (R + jωL) I˜
(1.21)
Abbildung 1.23: Zeitdiagramm von Strom und Spannung bei der Serienschaltung von Widerstand und Spule
i(t) = Iˆ sin(ωt) ,
ϕi = 0
u(t) = Û sin(ωt + ϕu ) ,
ϕu > 0
(1.22)
KAPITEL 1. OSZILLOSKOP
30
1.7.3 Allgemeines
Zu allen Zeigerdiagrammen lässt sich auch das duale Diagramm angeben.
$
1
ϕY = −ϕZ
⇒
Y=
Y = Z1
Z
(1.23)
Für das folgende Beispiel wird eine Impedanz mit positivem ϕZ gewählt (induktive Phasenverschiebung).
Abbildung 1.24: Zeigerdiagramme von Impedanz und Admittanz sowie von Strom und Spannung
Ob man den Stromzeiger oder den Spannungszeiger in die reelle Achse legt, ist prinzipiell egal,
fix ist nur die Phasenverschiebung zwischen Strom und Spannung ϕu − ϕi .
ϕi = 0
ϕu > 0
%
⇒
$
ϕZ = (ϕu − ϕi ) > 0
ϕY = (ϕi − ϕu ) < 0
=
ˆ
ϕu = 0
ϕi < 0
%
⇒
$
ϕZ = (ϕu − ϕi ) > 0
ϕY = (ϕi − ϕu ) < 0
(1.24)
Welche der beiden Möglichkeiten man wählt, hängt von der Schaltung ab, da entweder die
Spannung für beide Elemente die selbe ist und die Ströme komplex addiert werden müssen
(Parallelschaltung ⇒ Ũ in die reelle Achse legen) oder der Strom der selbe ist und die Spannungen verschieden sind (Serienschaltung ⇒ I˜ in die reelle Achse legen).
1.8. ÜBUNGSDURCHFÜHRUNG
31
1.8 Übungsdurchführung
1.8.1 Ausmessen einer symmetrischen Rechteckspannung
Aufgabenstellung
U
Messen Sie Amplitude 2pp (U pp ... U peak to peak ), Periodendauer T , Anstiegszeit trise und Abfallzeit t f all des Signals des Funktionsgenerators bei der maximal möglichen Frequenz und der
maximal möglichen Amplitude der Rechteckspannung.
Messaufbau
Verbinden Sie die Ausgänge des Funktionsgenerators (UA und Masse) mit dem Eingang CH1
des Oszilloskops. Stellen Sie am Generator fgrob auf ×2000, die Feineinstellung auf Maximum und den Wahlschalter für die Kurvenform auf symmetrisches Rechtecksignal. Stellen Sie
am Oszilloskop den Eingangswahlschalter auf DC und wählen Sie geeignete Einstellungen für
Empfindlichkeit und Zeitablenkung.
Messung
U
Messen Sie 2pp und T . Vergewissern Sie sich, dass die stufenlose Verstellung von Empfindlichkeit und Zeitbasis auf 1 bzw. CAL steht1 .
Zur Messung von trise und t f all verwenden Sie die verzögerte Zeitbasis (DELAY) bzw. die
ZOOM-Funktion 2 . Vergleichen Sie die automatische Messung mit Ihrer sorgfältigen Ablesung
am Schirmbild.
1.8.2 Laden und Entladen eines Kondensators
Wertangaben auf passiven Bauteilen
Bei dreistelligen Aufdrucken entspricht die letzte Ziffer dem Zehnerexponenten, wobei die Grundeinheit für Kondensatoren 1 pF und für Induktivitäten 1 µH beträgt.
Beispiele:
„223“ auf einem keramischen Kondensator bedeutet: 22 · 103 pF = 22 nF.
„332“ auf einer Induktivität bedeutet: 33 · 102 µH = 3,3 mH.
Die Bauteilwerte sind auf Normreihen abgestimmt. Beispielsweise sind in der E12-Reihe pro
i
Dekade 12 Werte vorgesehen, nämlich 10 12 mit i = 0 ... 11. Dies ergibt (gerundet): 1 1,2 1,5
1,8 2,2 2,7 3,3 3,9 4,7 5,6 6,8 und 8,2 .
1
Analoge Oszis haben zum Einstellen von Amplitude und Zeitbasis Stufenschalter mit einem kleineren aufgesetzten Drehregler. Mit diesem Drehregler kann eine stufenlose Feineinstellung erfolgen, die Skalierung auf
dem Bildschirm stimmt aber nur in einer bestimmten Position dieses Reglers (die sog. CALibrated–Position). Bei
digitalen Oszis gibt es diesen Regler nicht.
2 Sie können verzögerte Zeitbasis oder Zoom natürlich nicht nur hier, sondern auch bei allen weiteren Aufgaben
verwenden, um besonders interessante Kurventeile vergrößert darzustellen.
KAPITEL 1. OSZILLOSKOP
32
Aufgabenstellung
Nehmen Sie die Lade– und Entladekurve des 0,47 µF–Kondensators auf und berechnen Sie
daraus den Kapazitätswert. Nehmen Sie eine Skizze der beiden Kurven in das Protokoll auf.
Messaufbau
Zur Strommessung muss ein Shuntwiderstand Rshunt = 100 Ω laut Abbildung 1.25 vorgesehen
shunt
werden. Daraus folgt I = URshunt
. „DUT“ bezeichnet das Messobjekt („device under test“). Als
Spannungsversorgung wird das unsymmetrische Rechtecksignal des Funktionsgenerators bei
1 kHz verwendet. Wählen Sie die Amplitude so groß, dass am Messobjekt 5 V anliegen.
Abbildung 1.25: Messaufbau zur Strom-/Spannungsmessung am Oszilloskop
Da die Masseleitungen der beiden Oszilloskopeingänge intern miteinander verbunden sind,
muss die Schaltung gemäß Abbildung 1.25 verwendet werden. Um die verkehrte Polarität des
Spannungssignals am Shunt bei diesem Aufbau zu berücksichtigen, wird der zweite Kanal invertiert (CH2 INVERT). Der Aufbau nach Abbildung 1.25 funktioniert nur, da der Funktionsgenerator netzgetrennt und seine Masse daher nicht mit Erde verbunden ist. Andernfalls läge der
Shuntwiderstand mit beiden Anschlüssen auf Erdpotenzial und die Strommessung wäre damit
unmöglich.
Messung
Nehmen Sie den zeitlichen Verlauf von I und U auf und zeichnen Sie die Kurvenverläufe auf
Millimeterpapier. Zur Berechnung von C wird die e–Potenz ausgewertet. Am Analogoszillsokop messen Sie die Zeitkonstante τ, indem Sie eine Flanke am Schirm dehnen, bis sie in das
Raster des Oszilloskopschirmes passt. Nach der Zeit τ ist die e–Potenzkurve auf e−1 , das heißt
auf das 1e –fache abgefallen bzw. auf 1 − 1e (≈ 63 %) angestiegen. Es kann also τ an jenem Punkt
abgelesen werden, an dem die Kurve die entsprechende Prozentmarke schneidet. Am Digitaloszillsokop nehmen Sie die Cursor zu Hilfe.
Da der Beginn der Kurve meist verschliffen ist, muss für eine genaue Messung eine andere
Vorgangsweise gewählt werden. U∞ sei die Endspannung nach Abklingen des Lade– bzw. Entladevorganges. Messen Sie für zwei Zeitpunkte t1 und t2 die zugehörigen Spannungswerte U (t1)
und U (t2). Aus
t
(1.25)
U (t) −U∞ = ∆U0 e− τ
1.8. ÜBUNGSDURCHFÜHRUNG
33
ergibt sich aus der Division der zwei Gleichungen für die zwei Messpunkte
t1 −t2
U (t1) −U∞
= e− τ
U (t2) −U∞
τ=
ln
&
t2 − t1
U(t1 )−U∞
U(t2 )−U∞
'
(1.26)
(1.27)
Messen Sie τ auch mit dieser Methode, wobei Sie für die zwei Messpunkte jene für ungefähr 13
und 23 des Gesamthubs verwenden.
Berechnen Sie aus τ und R die Kapazität C und vergleichen Sie diesen Wert mit dem Aufdruck
und messen Sie den Kondensator mit dem mit dem Multimeter nach. Kommentieren Sie Abweichungen (welche Rolle spielt der Ausgangswiderstand der Signalquelle?).
Hinweis: Verwenden Sie auch bei den folgenden Aufgaben einen Shuntwiderstand von 100 Ω
zur Strommessung.
1.8.3 R, L und C im Wechselstromkreis
Aufgabenstellung
Messen Sie Strom, Spannung und Phasenwinkel und zeichnen Sie die maßstäblichen Zeigerdiagramme von Strom und Spannung für R, ZL und ZC für R = 680 Ω, L = 40 mH (im Übungsbrett
integriert) und C = 1 µF bei einer Frequenz des Sinussignals von f = 1 kHz. Bestimmen Sie die
Verlustfaktoren von Spule und Kondensator.
Erstellen Sie aus den gemessenen Werten ein Zeigerdiagramm für die Impedanzen von R, L
und C und ein Zeigerdiagramm für die Admittanzen von R, L und C unter Berücksichtigung der
Verlustwinkel.
Berechnen Sie die Blindwiderstände XL und XC aus den gemessenen Strömen und Spannungen
und berechnen Sie daraus zur Kontrolle C und L.
Messaufbau
Für diese Messung wird dieselbe Schaltung wie für die Lade- und Entladevorgänge (Punkt 1.8.2)
verwendet. Als DUT wird die zu messende Impedanz (R, L oder C) eingesetzt. Als Spannungsversorgung wird der Sinusausgang des Funktionsgenerators verwendet.
Messung
Für alle Messungen sei die Spannung am DUT konstant (U pp = 10 V). Wegen des Spannungsabfalles am Shunt muss bei jeder Messung nachjustiert werden.
Für die Zeigerdiagramme von Strom und Spannung legen Sie den Stromzeiger in die reelle
Achse. Der Verlustfaktor ist definiert durch
Verlustfaktor = tan(δ)
(1.28)
wobei δ den Verlustwinkel bezeichnet. Ist ϕ der Phasenwinkel zwischen Strom und Spannung,
so gilt
(1.29)
δ = 90◦ − |ϕ|
KAPITEL 1. OSZILLOSKOP
34
1.8.4 RLC–Kombination
Aufgabenstellung
Messen Sie Strom, Spannung und Phasenwinkel der Parallelschaltung von R = 680 Ω, L =
40 mH und C = 1 µF bei einer Frequenz des Sinussignals von f = 1 kHz. Erstellen Sie aus den
gemessenen Werten ein maßstäbliche Zeigerdiagramm für die Admittanz. Vergleichen Sie das
Ergebniss mit den Ergebnissen aus Punkt 1.8.3, indem sie die in 1.8.3 einzeln gemessenen Werte
für R,L,C graphisch addieren und zusätzlich in das Diagramm eintragen.
Messaufbau
Für diese Messung wird dieselbe Schaltung wie für die Lade– und Entladevorgänge (Punkt
1.8.2) verwendet. Als DUT wird die zu messende Impedanz (R)L)C) eingesetzt. (Der Shuntwiderstand sollte wieder auf 100 Ω erhöht werden.)
Messung
Führen Sie die Messung wie unter Punkt 1.8.3 durch und erstellen Sie das Zeigerdiagramm
aus den gemessenen Werten. Kontrollieren Sie das Diagramm, indem Sie die Ergebnisse von
Punkt 1.8.3 eintragen.
1.8.5 Schaltvorgang an einer RLC–Kombination
Aufgabenstellung
Nehmen Sie den zeitlichen Verlauf von Strom und Spannung nach einem Schaltvorgangs an
einer RLC–Kombination auf. Als DUT wird eine LC–Kombination mit L = 40 mH und C =
0,22 µF verwendet, Rshunt wird durch einen 10 Ω Widerstand ersetzt. Stellen Sie am Funktionsgenerator ein symmetrisches Rechtecksignal mit einer Frequenz von etwa 100 Hz ein. Bestimmen Sie die Resonanzfrequenz und die Dämpfungskonstante der Eigenschwingung.
Messaufbau
Verwenden Sie für diese Messung eine Schaltung ähnlich der aus Punkt 1.8.2. Als DUT wird
eine LC–Kombination mit L = 40 mH 3 und C = 0,22 µF eingesetzt, Rshunt wird durch einen
10 Ω Widerstand ersetzt.
Messung
Beobachten Sie die Verläufe der Kondensatorspannungen sowie des Stromes im DUT bei steigender Flanke des Rechteckssignals. Zeichnen Sie diese auf Millimeterpapier oder mitgebrachte Oszi–Schirm–Vordrucke. Bestimmen Sie aus den Kurven die Frequenz der auftretenden
Schwingung und die Dämpfungskonstante. Hinweis: Verwenden Sie zum Bestimmen der Zeiten
und Amplituden die Cursor–Funktion des Oszilloskops.
Überprüfen Sie rechnerisch anhand der Bauteilwerte ob die Dämpfung richtig gemessen wurde.
Kommentieren und begründen Sie Abweichungen.
3 Manche
Labor–Boards haben keine eingebaute Induktivität mit 40 mH. Verwenden Sie in diesem Fall eine
steckbare Induktivität mit 60 mH.
1.8. ÜBUNGSDURCHFÜHRUNG
35
1.8.6 Ausmessen einer unbekannten Kombination
Aufgabenstellung
Messen Sie Strom, Spannung und Phasenwinkel einer unbekannten RL– oder RC–Kombination
und finden Sie heraus, ob es sich bei der Kombination um eine Serien- oder eine Parallelschaltung handelt.
Messaufbau und Messung
Verwenden Sie denselben Aufbau und dieselben Messmethoden wie unter den Punkten 1.8.3
und 1.8.4 (Sinussignal!). Die unbekannte Kombination (Z x) wird Ihnen vom Praktikumsbetreuer gegeben. Bestimmen Sie aus dem Phasenwinkel, ob es sich um eine kapazitive oder
induktive Schaltung handelt und bestimmen Sie die Werte der Elemente im entsprechenden
Eratzschaltbild (RS, P und LS, P bzw. RS, P und CS, P der Serien- oder Parallelersatzschaltung)
gemäß Punkt 1.7.
Messung im xy–Betrieb
Vermessen sie das Bauteil auch im xy–Modus des Oszilloskops und vergleichen sie die Ergebnisse. Passen sie ihren Messaufbau so an, dass auf der horizontalen Achse die Spannung und
auf der vertikalen Achse der Strom dargestellt wird. Achten sie dabei auch auf die richtigen
Vorzeichen!
1.8.7 Beobachten von nichtlinearem Verhalten
Vom Praktikumsbetreuer erhalten sie ein unbekanntes Bauteil (NZ x). Untersuchen sie das Verhalten dieses Bauteils im xy–Betrieb bei Veränderung der Spannungsamplitude des Funktionsgenerators.
Dokumentieren sie das Verhalten durch Anfertigung geeigneter Diagramme und beschreiben
sie es in Stichworten (z.B. Strom steigt proportional/exponentiell mit Spannung...). Sie sollen
nicht bestimmen um welches Bauteil es sich handelt sondern nur das Verhalten beschreiben.
Überlegen sie, welchem Zweck dieses Bauteil in einer Schaltung dienen könnte.
KAPITEL 1. OSZILLOSKOP
36
1.9 Fragen
Die Fragen dienen der Vorbereitung auf das Praktikum und stellen nicht notwendigerweise Prüfungsfragen dar. Nicht alle Fragen können ausschließlich mit den Informationen aus dem Skriptum beantwortet werden. Recherchieren sie selbstständig und diskutieren sie mit Kollegen!
• Sie wollen mit dem Oszi den Wechselstrom des Stromnetzes überprüfen. Was müssen sie
dabei beachten?
• Zeichnen sie das Zeigerdiagramm der Admittanz einer Parallel– sowie Serienschaltung
von C = 100 nF und R = 1 kΩ bei f = 1kHz.
• Skizzieren sie das Schirmbild eines Oszis im xy–Betrieb beim Vermessen eines reellen
Widerstandes. (Schaltung lt. Abb. 1.25.)
• Skizzieren sie die Lissajous–Figur für folgende Signale:
CH1 = sin(ωt)
CH2 = cos(2ωt + π4 )
• Sie vermessen mit dem Oszi die Betriebsspannung einer Schaltung (5 Volt DC). Das
Oszi zeigt einen Mittelwert von nur 2 mV an, die Schaltung funktioniert aber und die
Messleitung ist korrekt angeschlossen. Worauf deutet das hin?
• Wozu dienen die 10% und 90% Marken im Raster des Schirmes eines analogen Oszilloskops?
• Ein Zweipol nimmt bei Anlegen einer Wechselspannung einen Strom mit einer Phasenlage ϕu − ϕi = −30◦ auf. Verhält sich der Zweipol induktiv oder kapazitiv? Wird der
Phasenwinkel größer oder kleiner werden, wenn man die Frequenz der Spannung erhöht?
• Was wird mit dem "‘Triggerpegel"’ eingestellt?
• Welche Rolle spielt der Triggerpegel im xy–Betrieb?
INSTITUT FÜR MIKROELEKTRONIK UND MIKROSENSORIK
JOHANNES KEPLER UNIVERSITÄT LINZ
Praktikum Elektrotechnik
WS 2013
Protokoll
Übung 1: Oszilloskop
Übungsdatum
Abgabedatum
Name
Name
Matr.Nr.
Matr.Nr.
Unterschrift
Unterschrift
39
Kapitel 2
Netzwerke und Drehstrom
2.1 Ersatzspannungsquelle
2.1.1 Theorie
Ein Satz der Netzwerktheorie, dessen Ableitung und Beweis den Rahmen dieses Skriptums
sprengen würde, besagt, dass jedes lineare Netzwerk in seiner Eigenschaft, bezogen auf zwei
Anschlüsse (Klemmen), durch eine Ersatzschaltung dargestellt werden kann, die
- entweder aus einer idealen Spannungsquelle mit einem Serienwiderstand
- oder aus einer idealen Stromquelle mit einem Parallelwiderstand
besteht (ideale Spannungsquellen liefern Spannung unabhängig vom Laststrom, ideale Stromquellen liefern Strom unabhängig von der Lastspannung). Linear bedeutet hier, dass das Netzwerk aus idealen R, L, C, Spannungs- und Stromquellen besteht und insbesondere, dass R, L
und C konstant sind und nicht spannungs- oder stromabhängig.
Ri
Ia
Ia
Ik
Ul
Ua
=
Ri
Ua
Abbildung 2.1: Äquivalenz des Klemmenverhaltens von Ersatzspannungsquelle (Leerlaufspannung Ul ) und Ersatzstromquelle (Kurzschlussstrom Ik ).
Häufig interessiert an einem komplizierten Netzwerk nur dessen elektrisches Verhalten (Zusammenhang zwischen Strom und Spannung) in einem Zweig bzw. zwischen zwei Klemmen. Der
Satz von der Ersatzspannungs- bzw. Stromquelle besagt nun, dass sich jedes lineare Netzwerk,
auch wenn es noch so kompliziert ist, auf ein Ersatzschaltbild (ESB) entsprechend Abbildung
2.1 zurückführen lässt. Dieses gilt dann natürlich nur bezüglich dieser beiden Klemmen, für
jedes andere Klemmenpaar kann aber genauso ein ESB gefunden werden. Selbstverstädlich gilt
KAPITEL 2. NETZWERKE UND DREHSTROM
40
dies auch für Netzwerke mit Kapazitäten und Induktivitäten so lange diese in ihren linearen
Bereichen betrieben werden (Stichwort Sättigung).
Wie aus dem Ersatzschaltbild ersichtlich ist, ändert sich die Klemmenspannung Ua linear mit
dem Laststrom Ia (Ua = Ul − Ia Ri , Ri ist der Innenwiderstand der Ersatzspannungsquelle). Enthält das Netzwerk jedoch auch nichtlineare Elemente, so gilt der Satz von der Ersatzspannungsquelle nicht mehr. Hier bietet sich aber die Möglichkeit ein lineares Kleinsignal–ESB für einen
bestimmten Arbeitspunkt, in dem die nichtlinearen Bauelemente betrieben werden, zu bestimmen. Alle nichtlinearen Kennlinien werden dann in der Umgebung des Arbeitspunktes linear
approximiert. Voraussetzung für die Gültigkeit eines solchen Kleinsignal–ESB ist natürlich,
dass sich Ströme und Spannungen gegenüber dem Arbeitspunkt nur geringfügig ändern.
Die Spannung der Ersatzspannungsquelle ist gleich der Leerlaufspannung (Ia = 0) der beiden
Netzwerkklemmen, der Strom der Ersatzstromquelle ist gleich dem Kurzschlussstrom (Ua = 0)
der Netzwerkklemmen. Der Kurzschlussstrom kann nur in den seltensten Fällen direkt gemessen werden (z. B. sind die Sicherungen und Zuleitungen einer normalen Netzsteckdose nicht
geeignet, den Kurzschlussstrom zu führen!). Kurzschlussstrom und Leerlaufspannung hängen
wie folgt zusammen
Ul = Ik Ri .
(2.1)
Ist das Netzwerk bekannt, so kann der Widerstand Ri einfach bestimmt werden: Jede Spannungsquelle wird durch einen Kurzschluss und jede Stromquelle durch einen Leerlauf ersetzt.
Durch Zusammenfassung der so erhaltenen Schaltung zwischen den Klemmen ergibt sich Ri .
Diese Vorgangsweise soll an folgendem Beispiel gezeigt werden.
R1
Ia
Uq
R2
Ri
Ua
=
Ul
Ia
Ua
Abbildung 2.2: Ersatzspannungsquelle für einen Spannungsteiler
Die Quellenspannung der Ersatzquelle ergibt sich zu
Ul = Uq
R2
.
R1 + R2
(2.2)
Zur Bestimmung des Widerstandes wird die Spannungsquelle im Netzwerk durch einen Kurzschluss ersetzt. Dann erscheint an den Klemmen die Parallelschaltung von R1 und R2 . Daher ist
der Widerstand
R1 R2
.
(2.3)
Ri =
R1 + R2
2.1. ERSATZSPANNUNGSQUELLE
41
Ist das Netzwerk nicht bekannt und kann der Kurzschlussstrom nicht gemessen werden, so muss
aus der linearen Abhängigkeit der Ausgangsspannung Ua vom Laststrom Ia auf den Widerstand
Ri und in weiterer Folge auf Ik rückgerechnet werden. Man misst also die Klemmenspannung
bei einem bekannten Laststrom Ia und erhält mit der zuvor gemessenen Leerlaufspannung aus
der Gleichung Ua = Ul − Ia Ri den Innenwiderstand Ri . Es empfiehlt sich, diese Messung bei
verschiedenen Lastströmen zu wiederholen, um zu kontrollieren, ob sich das Netzwerk wirklich
linear verhält.
Das Superpositionsprinzip (Satz von Helmholtz)
Enthält ein Netzwerk mehrere Strom- und/oder Spannungsquellen, dann kann der Strom bzw.
die Spannung in einem Zweig des Netzwerks durch Superposition der Wirkungen der einzelnen
Quellen bestimmt werden. Die Vorgangsweise ist wie folgt: Alle bis auf eine Quelle im Netzwerk werden entfernt (d. h. Spannungsquellen werden durch Kurzschlüsse und Stromquellen
durch Leerläufe ersetzt). Nun wird im interessanten Zweig der Strom oder die Spannung zufolge der übriggebliebenen Quelle bestimmt. Dieser Vorgang wird für alle anderen Quellen im
Netzwerk wiederholt. Am Schluss werden die Teilströme bzw. -spannungen im Zweig aufaddiert. Die so gewonnenen Größen entsprechen jenem Zweigstrom oder jener Zweigspannung,
die zu beobachten sind, wenn alle Quellen im Netzwerk in Betrieb sind. Voraussetzung für die
Anwendung des Superpositionsprinzips ist die Linearität des Netzwerkes.
2.1.2 Spannungs– und stromrichtiges Messen
Für die oben erwähnte messtechnische Bestimmung von Ri müssen Strom und Spannung am
Lastwiderstand gleichzeitig bestimmt werden. Dazu sind grundsätzlich zwei Schaltungsvarianten möglich (siehe Bild 2.3).
Uerr
A
IR
V
R UR
a)
A
Ierr
V
IR
R UR
b)
Abbildung 2.3: a) Stromrichtiges und b) spannungsrichtiges Messen
Beim stromrichtigen Messen ist der gemessene Strom identisch (abgesehen vom Messfehler des
Instrumentes) mit jenem durch den Widerstand. Die Spannung am Voltmeter ist um den Betrag
des Spannungsabfalls am Innenwiderstand des Amperemeters größer als jene am Widerstand.
Wird spannungsrichtig gemessen, so sind die Spannungen am Voltmeter und am Widerstand
gleich, das Amperemeter misst aber die Summe der Ströme durch den Widerstand und durch
das Voltmeter. Je nach Größe des Widerstandes liefern die beiden Methoden unterschiedlich
genaue Ergebnisse. Ist der Widerstand groß, so hat der zusätzliche kleine Innenwiderstand des
Amperemeters bei der stromrichtigen Methode nur wenig Einfluss. Wird aber spannungsrichtig
KAPITEL 2. NETZWERKE UND DREHSTROM
42
gemessen, kann der hohe Innenwiderstand des Voltmeters parallel zum ebenfalls hohen Lastwiderstand den gemessenen Strom deutlich verfälschen. Bei kleinen Lastwiderständen sind die
Verhältnisse genau umgekehrt. Für besonders genaue Messungen können durch die Berücksichtigung der Innenwiderstände der Messgeräte die Messwerte noch korrigiert werden.
2.2 Leistungsanpassung
Abbildung 2.4: Leistungsanpassung bei einem Generator mit Innenwiderstand Ri
Während von Spannungsquellen üblicherweise ein sehr geringer (idealerweise verschwindender) und von Stromquellen ein sehr großer (idealerweise unendlicher) Innenwiderstand erwartet
wird, gibt es auch Situationen, in denen das Auftreten eines nicht vernachlässigbaren Generatorwiderstandes unvermeidbar oder sogar erwünscht ist. Ein typisches Beispiel dafür ist die
Hochfrequenztechnik, in der zumeist mit Innenwiderständen von 50 Ω gearbeitet wird. In diesem Fall ist es von großem Interesse herauszufinden, wie sich der Innenwiderstand des Generators und eine daran angeschlossene Last zueinander verhalten müssen, um dem Generator die
maximal mögliche Leistung zu entnehmen. Abbildung 2.4 zeigt die eben beschriebene Situation eines Generators mit Leerlaufspannung U0 und Innenwiderstand Ri , an den eine Last RL
angeschlossen wird. Aus der Spannungsteilerregel ergibt sich die Spannung an der Last zu
UL =
RL
U0
Ri + RL
(2.4)
und aus einem einfachen Maschenumlauf der Laststrom zu
IL =
U0
.
Ri + RL
(2.5)
Die an die Last abgegebene Leistung errechnet sich dann zu
PL = UL IL = U02
RL
(Ri + RL )2
.
(2.6)
Durch Differenzieren von Gleichung 2.6 nach RL und Nullsetzen folgt die Bedingung für maximale Leistung zu
RL = Ri .
(2.7)
Hinweis: Versuchen Sie zur Vorbereitung auf das Praktikum diese Ableitung vollständig durchzuführen!
2.3. SPANNUNGSTEILER
43
Besonders soll noch darauf hingewiesen werden, dass für die reflexionsfreie Anpassung von
Leitungen an Generatoren und Empfänger das gleiche Ergebnis gefunden wird. Dies ist wiederum in der Hochfrequenztechnik von außerordentlicher Wichtigkeit, da es bedeutet, dass durch
eine Leitung die reflexionsfrei an Generator und Last angepasst ist, gleichzeitig die maximal
mögliche Leistung übertragen wird.
Anmerkung: In der Energietechnik ist man nicht an der Maximierung der übertragbaren Leistung interessiert, sondern an der Minimierung der auftretenden Verluste. Bei Leistungsanpassung verliert man 50% der erzeugten Energie durch die Übertragung, dies wäre für das Stromnetz (und den Strompreis) fatal!
2.3 Spannungsteiler
2.3.1 Unbelasteter und belasteter Spannungsteiler
Für diesen Übungsteil ist das Wissen um Serien- und Parallelschaltung von Widerständen, wie
es in den Übungen zur Vorlesung ausführlichst behandelt wurde, ausreichend.
2.4 Frequenzunabhängiger Spannungsteiler
2.4.1 Theorie
Für die Messung bei höheren Frequenzen werden häufig frequenzkompensierte Spannungsteiler
(z. B. Eingangsabschwächer oder Oszilloskoptastköpfe) verwendet. Diese bestehen aus der Parallelschaltung eines Widerstands- und eines Kapazitätsspannungsteilers (Bild 2.5) Wenn beide
Abbildung 2.5: Frequenzkompensierter Spannungsteiler
2
genau dasselbe Spannungsteilerverhältnis haben, so gilt RR12 = C
C1 und das Übertragungsmaß ist
theoretisch vollkommen frequenzunabhängig (zur Vertiefung des Verständnisses wird empfohlen, den Spannungsteiler ausführlich nachzurechnen). Das ist gleichbedeutend damit, dass der
obere und der untere Teil des Spannungsteilers die gleiche Zeitkonstante haben (τ1 = R1C1 =
τ2 = R2C2 ). Die bei sehr hohen Frequenzen trotzdem auftretenden Abweichungen sind durch
die inneren Frequenzabhängigkeiten der Bauteile und durch vorhandene parasitäre Induktivitäten gegeben. Am besten lässt sich die korrekte Frequenzkompensation mit einem rechteckförmigen Signal überprüfen, da dieses auch sehr hohe Frequenzen enthält. Einen entsprechenden
Kurvenverlauf zeigt Bild 2.6.
Da im Messbetrieb der Spannungsteilerabgriff belastet wird (mit einem Kabel und einem Verstärkereingang), muss dieser Lastwiderstand (R und C) berücksichtigt werden. Daher ist bei
KAPITEL 2. NETZWERKE UND DREHSTROM
44
Abbildung 2.6: Ausgangsspannung für über-, unter- und richtig kompensierten Spannungsteiler
Oszilloskoptastköpfen einer der beiden Parallelkondensatoren einstellbar ausgeführt um den
Spannungsteiler an das Kabel und den Verstärkereingang anzupassen.
Der wichtigste Verwendungszweck von Tastköpfen, die einen Vorschaltspannungsteiler (meist
1/10) darstellen, ist es, die kapazitive Belastung des Messobjektes zu verkleinern.
Abbildung 2.7: Gesamtschaltung Oszilloskoptastkopf mit Kabel und Oszilloskop
Die Eingangskapazität Ce ergibt sich dabei aus der Serienschaltung der Kompensationskapazität
C1 mit C2 des Spannungsteilers samt der parallelliegenden Kabel- und Eingangskapazität des
Oszilloskops.
1
1
1
=
+
(2.8)
Ce C1 C2 +CK +CeOsz
Die kapazitive Belastung wird also annähernd um das Spannungsteilerverhältnis kleiner als die
Eingangskapazität des Oszilloskops mit dem Kabel ohne Tastkopf. Vor der Messung mit Tastköpfen ist immer darauf zu achten, dass sie richtig kompensiert sind. Dazu stellen die meisten
Oszilloskope eine Rechteckspannung zur Verfügung.
2.5 Drehstrom
2.5.1 Wechselstromkenngrößen
Für die Messung eines Signals nach Abbildung 2.8 werden verschiedene Kenngrößen definiert.
Als Beispiel wird ein Stromsignal i(t) gewählt. Die Periodendauer wird mit τ = 1f bezeichnet.
Der Maximalwert des Stromes ist imax , der Minimalwert imin .
2.5. DREHSTROM
45
Abbildung 2.8: Zeitdiagramm eines allgemeinen periodischen Signals
Gleichwert
Den arithmetischen Mittelwert ī bezeichnet man als Gleichwert. Er wird durch Integration über
eine Periode berechnet.
t!0 +τ
!τ
1
1
i(t)dt =
i(t)dt
(2.9)
ī =
τ
τ
t0
0
Gleichrichtwert
Wird das Signal vor der Mittelwertberechnung gleichgerichtet, so erhält man den Gleichrichtwert |i|.
1
|i| =
τ
!τ
0
1
|i(t)|dt =
τ
t!0 +τ
t0
|i(t)|dt
(2.10)
Bemerkung: Allgemein gilt |i| *= | ī |.
Effektivwert
Die wichtigste Kenngröße für Wechselstrom ist der Effektivwert Ie f f . Würde ein Gleichstrom
der Höhe I = Ie f f durch einen Widerstand fließen, so wäre die in Wärme umgesetzte Leistung
die gleiche wie für den Wechselstrom i(t).
(
(
) t0 +τ
) τ
) !
) !
1
)1
)
[i(t)]2 dt = *
[i(t)]2 dt
(2.11)
Ie f f = *
τ
τ
t0
0
Im Folgenden wird bei Effektivwerten der Index „eff “ weggelassen.
Spitze-Spitze, Brumm
Der Gesamthub des Signales zwischen maximalem und minimalem Wert heißt i pp oder iss (peak
to peak ... Spitze-Spitze). Bei Gleichströmen und Gleichspannungen, welchen nur ein kleines
Wechselsignal überlagert ist, spricht man von Brumm.
i pp = imax − imin
(2.12)
KAPITEL 2. NETZWERKE UND DREHSTROM
46
Sinusförmige Wechselgröße
Abbildung 2.9: Zeitdiagramm eines Sinussignales
Handelt es sich um ein rein sinusförmiges Signal i(t) = Iˆ sin(ωt + ϕ) mit der Amplitude (dem
Scheitelwert) Iˆ nach Abbildung 2.9, so gelten folgende Beziehungen:
ī = 0
1
I = Iˆ √
2
2
|i| = Iˆ
π
i pp = 2 Iˆ
(2.13)
(2.14)
(2.15)
(2.16)
2.6 Leistungsmessung bei Sinusgrößen
Wird an einen Verbraucher eine sinusförmige Wechselspannung gelegt, so fließt durch ihn ein
ebenfalls sinusförmiger Wechselstrom. Ist der Verbraucher nicht rein ohmsch, ergibt sich eine
Phasenverschiebung ϕ = ϕu − ϕi zwischen Strom und Spannung. Bei induktiver Last ist ϕ positiv, bei kapazitiver Last negativ. Abbildung 2.10 zeigt die Zeitdiagramme von Spannung und
Strom.
Abbildung 2.10: Spannung und Strom einer Impedanz
Multipliziert man die Effektivwerte von Strom I und Spannung U ohne Berücksichtigung der
Phasenverschiebung, so erhält man die Scheinleistung S (PS ). Der ohmsche Anteil der Leistung
2.7. DREIPHASENWECHSELSTROM
47
heißt Wirkleistung P (PW ), der Blindanteil Blindleistung Q (PB ).
S =UI,
P = U I cos(ϕ) ,
Q = U I sin(ϕ) ,
[S] = 1 VA
[P] = 1 W
[Q] = 1 var .
(2.17)
(2.18)
(2.19)
Abbildung 2.11: Zusammenhang zwischen Schein-, Wirk- und Blindleistung
Diese Beziehungen können durch ein Dreieck laut Abbildung 2.11 dargestellt werden. Der Zusammenhang zwischen S, P und Q ergibt sich daraus zu
+
(2.20)
S = P 2 + Q2 .
2.7 Dreiphasenwechselstrom
2.7.1 Einführung
Drehstromsysteme entstehen durch Zusammenschalten mehrerer phasenverschobener Spannungen. Das gebräuchlichste Drehstromsystem, das in der Regel auch im öffentlichen Stromversorgungsnetz eingesetzt wird, liefert drei sinusförmige Wechselspannungen, die miteinander
verkettet und um 120◦ gegeneinander phasenverschoben sind.
Abbildung 2.12: Zeitdiagramm der drei Spannungen eines Drehstromsystems
In der Abbildung 2.12 sind die drei Spannungen als Zeitdiagramm u(t) und in der Abbildung 2.13 als Zeigerdiagramm dargestellt.
48
KAPITEL 2. NETZWERKE UND DREHSTROM
Abbildung 2.13: Zeigerdiagramm der drei Spannungen eines Drehstromsystems
Bei den Spulen des Drehstromgenerators und auf der Verbraucherseite beim Anschluss von
z. B. Motoren sind grundsätzlich zwei Schaltungsarten üblich, nämlich die Sternschaltung und
die Dreieckschaltung. In der Abbildung 2.14 sind diese zwei Möglichkeiten dargestellt.
Abbildung 2.14: Sternschaltung und Dreieckschaltung.
Die Leiter werden folgendermaßen bezeichnet:
L1, L2, L3 Phasen, Leiter
N Neutralleiter
UL1,L2 , UL2,L3, UL3,L1 verkettete Spannungen, Außenleiterspannungen,
spannungen
UL1,N , UL2,N , UL3,N Phasenspannungen, Sternspannungen,
Dreieck-
wobei statt UL1,N , UL2,N und UL3,N auch U1 , U2 und U3 geschrieben wird. Als Strangspannung
wird jeweils die Spannung an den Anschlüssen eines Stranges bezeichnet. Je nach Schaltung
kann die Strangspannung daher gleich der Außenleiterspannung oder der Phasenspannung sein.
2.7. DREIPHASENWECHSELSTROM
49
2.7.2 Spannungen und Phasenlage
Die von einem Drehstromgenerator erzeugten drei sinusförmigen und um 120◦ phasenverschobenen Wechselspannungen sind so miteinander verkettet, dass drei Strangspannungen und
drei verkettete Spannungen abgegriffen werden können. Das Spannungszeigerdiagramm (Abbildung 2.15) zeigt die Zusammenhänge zwischen den Spannungen in Bezug auf Größe und
Phasenlage.
Abbildung 2.15: Komplettes Zeigerdiagramm der Spannungen in einem Drehstromnetz
Der Zusammenhang zwischen Phasenspannung ULN und verketteter Spannung ULL lässt sich
leicht aus dem Zeigerdiagramm ablesen
ULL
= ULN sin (60◦ )
2
⇒
ULL =
√
3ULN .
(2.21)
Üblicherweise werden die Spannungen in Effektivwerten angegeben. Im öffentlichen Versorgungsnetz gilt daher ULN = 230 V und ULL = 400 V (früher 220 V / 380 V).
2.7.3 Leistungsmessung in Dreileitersystemen - Aronschaltung
Für die Bestimmung der Gesamtleistung in einem Drehstromdreileitersystem ist die Messung
von 2 Spannungen und 2 Strömen ausreichend. Das lässt sich für die Sternschaltung (vgl. Abbildung 2.14) wie folgt sehen: Die gesamte komplexe Leistung im System ist
S = U L1, N I ∗1 +U L2, N I ∗2 +U L3, N I ∗3
¯
¯
¯
¯
¯
¯
¯
(2.22)
wobei I X der Strom in der Phase LX ist und „ ∗ “ die komplexe Konjugation bezeichnet. Da im
¯
Dreileitersystem
kein Neutralleiter vorhanden ist, muss die Beziehung
I1 + I2 + I3 = 0
¯
¯
¯
⇒
I ∗1 + I ∗2 + I ∗3 = 0
¯
¯
¯
(2.23)
gelten. Wird I3 aus dieser Gleichung ausgedrückt und in die Leistungsgleichung eingesetzt, so
erhalten wir
,
,
S = I ∗1 U L1, N −U L3, N + I ∗2 U L2, N −U L3, N = I ∗1U L1, L3 + I ∗2U L2, L3 .
(2.24)
¯ ¯
¯ ¯
¯ ¯
¯ ¯ ¯
¯
¯
KAPITEL 2. NETZWERKE UND DREHSTROM
50
A
L1
V
I1
L1
UL3, N
UL1, L3
UL1, N
A
V
V
UL2, L3
A
UL2, N
V
L2
I3, 1
I3
L3
I2
I1, 2
UL1, L3
I3
L3
L2
I1
UL2, L3
A
I2, 3
I2
Abbildung 2.16: Aronschaltung
Durch Messung von 2 Strangströmen und 2 verketteten Spannungen entsprechend Abbildung 2.16
ist es also möglich, auf die Gesamtleistung im dreiphasigen Verbraucher zu schließen. Da Ströme und Spannungen multipliziert werden, welche nicht an einem Strang (Zweipol) auftreten, ist
die Phasenverschiebung nicht gleich dem Phasenwinkel der Strangimpedanz. So ist beispielsweise bei Verwendung dreier gleicher, rein ohmscher Lastwiderstände die Phasenverschiebung
zwischen I1 und UL1, L2 30◦ .
Eine ähnliche Ableitung ist im Fall der Dreieckschaltung des Verbrauchers möglich. Hier gilt
S = U L1, L2 I ∗1, 2 +U L2, L3 I ∗2, 3 +U L3, L1 I ∗3, 1 ,
(2.25)
¯
¯
¯
¯
¯
¯
¯
wobei I X,Y der Strom in jenem Strang ist, der die Phase LX mit der Phase LY verbindet. Mit
¯
den Gleichungen
(2.26)
I 2, 3 = I 1, 2 + I 2 ⇒ I ∗2, 3 = I ∗1, 2 + I ∗2
¯
¯
¯
¯
¯
¯
sowie
(2.27)
I 3, 1 = I 1, 2 − I 1 ⇒ I ∗3, 1 = I ∗1, 2 − I ∗1
¯
¯
¯
¯
¯
¯
erhalten wir
,
(2.28)
S = U L2, L3 I ∗2 −U L3, L1 I ∗1 + I ∗1, 2 U L1, L2 +U L2, L3 +U L3, L1 .
¯- ¯
¯
¯
¯
¯
¯
¯
¯
,
Da U L1, L2 +U L2, L3 +U L3, L1 = 0 und U L1, L3 = −U L3, L1 gilt, ergibt sich wieder
¯
¯
¯
¯
¯
(2.29)
S = I ∗1U L1, L3 + I ∗2U L2, L3 .
¯ ¯
¯ ¯ ¯
Die im Drehstromsystem insgesamt umgesetzte Wirkleistung entspricht dann dem Realteil der
komplexen Gesamtleistung S während die Blindleistung durch den Imaginärteil von S gegeben
¯
¯
wird.
In der Praxis dient die Aronschaltung der Bestimmung der Wirkleistung mit einem Wattmeter.
Dabei misst man hintereinander die Wirkleistungen, die sich durch Verknüpfung der Spannungen und Ströme, wie soeben beschrieben, ergeben. Die Gesamtleistung ist dann die Summe der
Ergebnisse beider Messungen. Durch die im Drehstromsystem vorhandenen Phasenverschiebungen können bei den Einzelmessungen auch negative Werte auftreten. Diese Methode liefert
auch bei unsymmetrischer Last ein korrektes Ergebnis.
2.8. ÜBUNGSDURCHFÜHRUNG
51
2.8 Übungsdurchführung
2.8.1 Leistungsanpassung
Messen Sie die von einer Gleichspannungsquelle (U0 = 15 V, Ri = 1 kΩ; Ri muss der idealen
Spannungsquelle extern beigefügt werden!) an einen Lastwiderstand RL abgegebene Leistung
und bestätigen Sie so die Theorie der Leistungsanpassung. Der Innenwiderstand nach dieser Angabe muss extern vorgesehen werden, da die elektronisch stabilisierte Spannungsquelle einen
verschwindend kleinen Innenwiderstand aufweist. Überlegen Sie sich die passende Schaltung
sowie geeignete Lastwiderstände für eine Kennlinie P = f(RL ) mit mindestens 10 Messpunkten
inklusive . Überlegen Sie sich vor Beginn der Übung (zu Hause) sinnvolle Werte für die Lastwiderstände bzw. deren Kombinationen. Welche Messmethode ist für diese Messung besser,
Strom– oder Spannungsrichtige Messung? Zeichnen Sie U = f(RL ), I = f(RL ) und P = f(RL ) in
ein Diagramm. Ziehen sie eine logarithmische X–Achse in Betracht (was ist dann mit RL = 0?)!
2.8.2 Spannungsteiler
Ue
Vom Übungsleiter erfahren Sie zwei Parameter (R1, R2, Rges , Ra , U
) eines Spannungsteilers,
a
den sie dimensionieren sollen. Berechnen Sie die unbekannten Parameter und finden Sie die
entsprechende Kombination aus den vorhandenen Widerständen, um diesen Spannungsteiler zu
realisieren. Verlassen Sie sich aber nicht auf die aufgedruckten Werte, da die Widerstände einen
Toleranzbereich von 5% aufweisen, messen Sie die korrekten Werte zuerst mit dem Ohmmeter.
Kontrollieren Sie den so bestimmten Spannungsteiler durch die Messung von Ue und Ua .
Belasten Sie den Spannungsteiler von nun mit folgenden Lastwiderständen: 15 kΩ, 10 kΩ, 5 kΩ,
1 kΩ, 0,5 kΩ. Zeichnen Sie im Protokoll Ua als Funktion von RL und vergleichen Sie drei gemessene Werte mit den zugehörigen gerechneten.
2.8.3 Frequenzkompensierter Spannungsteiler
Entwerfen Sie mit den vorhandenen Kondensatoren und Widerständen einen frequenzkompensierten Spannungsteiler nach Abbildung 2.5 mit einem Teilerverhältnis von annähernd Ue /Ua =
3/1. Verwenden Sie als R1 einen Widerstand von 1 kΩ und, um den Spannungsteiler auch abgleichen zu können, das Potentiometer als R2 . ACHTUNG, bei Verwendung eines kleineren
Wertes als 1 kΩ für R1 kann wegen der auftretenden hohen Querströme das Potentiometer zerstört werden. Gleichen Sie den Spannungsteiler mit einer Rechteckspannung ( f = 1 kHz) ab
und messen Sie dann das tatsächliche Spannungsteilerverhältnis. Nehmen Sie je eine Skizze des
Schirmbildes für die drei verschiedenen Kompensationsfälle in das Protokoll auf. Beobachten
Sie das Verhalten des frequenzkompensierten Spannungsteilers auch bei sehr tiefen und sehr
hohen Frequenzen der Rechteckspannung. Was fällt Ihnen auf und wie können Sie eventuell
störende Phänomene bekämpfen (Kommentare ins Protokoll!).
2.8.4 Effektivwertmessung
Messen Sie die Amplitude Û und den Effektivwert U einer Sinusspannung und einer symmetrischen Rechteckspannung bei ca. 50 Hz. Verwenden Sie als Signalquelle den Funktionsgenerator
bei der maximalen Amplitude. Messen Sie mit dem Oszilloskop und mit dem Digitalmultimeter
und berechnen Sie aus beiden Messungen den Effektivwert. (Falls nötig auf AC schalten!)
KAPITEL 2. NETZWERKE UND DREHSTROM
52
Achtung: Es gibt zwei verschiedene Typen von Messgeräten. Die billigeren (AVG ... average,
z. B. Metex MX40) haben keine Möglichkeit der echten Effektivwertmessung, sondern zeigen
gemäß Gleichung (2.30) nur den Gleichrichtwert umskaliert auf den Effektivwert einer Sinusgröße an.
π 1
√
uAnzeige = |u| ·
(2.30)
2 2
Um den Effektivwert der Rechteckspannung mit diesem Multimeter messen zu können, muss
zuerst |u| aus Gleichung (2.30) berechnet werden. Überlegen Sie sich den Zusammenhang zwischen |u| und U und berechnen Sie so U . Vergleichen Sie den aus Û berechneten mit dem aus
uAnzeige berechneten Effektivwert.
Bessere Ausführungen von Messgeräten (True RMS ... root mean square, z. B. Metex MX47,
Fluke 175) quadrieren vor der Mittelung die Messgröße und können so auch bei nicht sinusförmigen Signalen den korrekten Effektivwert anzeigen. Voraussetzung dafür ist, dass der CrestFaktor Û/Ueff des Signales nicht zu groß ist. Der zulässige Crest-Faktor hängt vom konkret
verwendeten Messgerät ab. Messen Sie mit beiden Messgeräten und vergleichen Sie berechneten und abgelesenen Effektivwert.
2.8.5 Sternschaltung
Symmetrische Belastung mit Neutralleiter: Beschalten Sie den am Übungsbrett vorhandenen Drehstromgenerator mit drei Widerständen R á 1 kΩ in Vierleiter-Sternschaltung laut
Abbildung 2.17. Messen Sie die Strangströme IL1 , IL2 und IL3 , sowie den Nullleiterstrom IN mit
Abbildung 2.17: Messaufbau für Sternschaltung
den Digitalmultimetern. Berechnen Sie die gesamte umgesetzte Leistung PStern .
Symmetrische Belastung ohne Neutralleiter: Entfernen Sie den Neutralleiter und bestimmen Sie erneut die umgesetzte Leistung im Stern mit Hilfe der Aronschaltung. Wie bereits
in Abschnitt 2.7.3 ausgeführt worden ist, sind dabei die Außenleiterspannung UL1, L3 und der
Leiterstrom I1 nicht in Phase, was genauso für UL2, L3 und I2 gilt. Bei der Berechnung der Leistung nach Gleichung (2.18) muss diese Phasenverschiebung daher berücksichtigt werden und
es gilt cos(ϕ) *= 1. Würden Strom und Spannung nicht getrennt voneinander gemessen werden,
sondern statt dessen, wie in der Praxis üblich, ein richtiges Wattmeter eingesetzt, wäre diese
Korrektur nicht nötig, da dann die Phasenverschiebung vom Messgerät selbst berücksichtigt
wird.
2.9. FRAGEN
53
Unsymmetrische Belastung: Wiederholen Sie die beiden Messungen mit drei verschiedenen Widerstandswerten für R1 , R2 und R3 nach Angabe des Übungsleiters und zeichnen Sie
die Zeigerdiagramme für Ströme und Spannungen. Kontrollieren Sie für die Sternschaltung mit
Neutralleiter ∑ IL,i = IN und messen Sie bei der Sternschaltung ohne Neutralleiter die Sternpunktverschiebung (Spannung US, N zwischen dem Sternpunkt S und dem Neutralleiter N). Berechnen Sie die gesamte umgesetzte Leistung PStern . Da mit den vorhandenen Messgeräten die
Phasenbeziehungen zwischen Strömen und Spannungen nicht einfach gemessen werden können, kann die Aronschaltung hier nicht angewandt werden.
2.8.6 Dreieckschaltung
Symmetrische Belastung: Beschalten Sie den am Übungsbrett vorhandenen Drehstromgenerator mit drei Widerständen R á 1 kΩ in Dreieckschaltung laut Abbildung 2.18. Messen Sie
Abbildung 2.18: Messaufbau für Dreieckschaltung
die Leiterströme IL1 , IL2 und IL3 , sowie die Strangströme IR1 , IR2 und IR3 mit den Digitalmultimetern. Berechnen Sie die gesamte umgesetzte Leistung PDreieck und vergleichen Sie diese mit
PStern .
Bestimmen Sie die umgesetzte Leistung auch mit der Aronschaltung.
Unsymmetrische Belastung: Wiederholen Sie die Messung mit drei verschiedenen Widerstandswerten für R1 , R2 und R3 nach Angabe des Übungsleiters und zeichnen Sie das Zeigerdiagramm aller sechs Ströme. Kontrollieren Sie ∑ IL,i = 0. Überlegen Sie sich, für welche
Ströme (IL,i oder IR,i ) die Phasenbeziehung von 120◦ gelten muss. Berechnen Sie die gesamte
umgesetzte Leistung PDreieck . Die Aronschaltung ist hier aus den genannten Gründen ebenfalls
nicht anwendbar.
2.9 Fragen
Die Fragen dienen der Vorbereitung auf das Praktikum und stellen nicht notwendigerweise Prüfungsfragen dar. Nicht alle Fragen können ausschließlich mit den Informationen aus dem Skriptum beantwortet werden. Recherchieren sie selbstständig und diskutieren sie mit Kollegen!
• Unser Stromnetz hat eine Phasenspannung von 230 Volt (Leiter zu Neutralleiter). Zwischen zwei Leitern sind es 400 V *= 2 · 230 V. Wie kann das sein?
54
KAPITEL 2. NETZWERKE UND DREHSTROM
• Sie schließen einen Kondensator mit einer Spannungsfestigkeit von Umax = 250 V an das
Stromnetz an. Nach zwei Minuten explodiert er. Warum?
• Sie benötigen in einer Schaltung eine Betriebsspannung von 1 V bei einem Strom von
3 bis 10 mA. Sie haben eine Batterie mit 1,5 V. Kann diese Anpassung mittels eines
Spannungsteilers durchgeführt werden? Wenn ja, dimensionieren sie diesen.
• Der Maximalstrom der aus einer Schuko–Steckdose entnommen werden kann beträgt
16 A. Welche elektrische Leistung kann ein Gerät maximal aufnehmen?
• Wie groß ist die maximale Leistung bei Drehstrom (und 16 A Maximalstrom)? Ist das
von der Schaltung (Stern/Dreieck) abhängig?
• Wie ist der Effektivwert definiert und wie hängen Spitzenwert und Effektivwert bei einer
a) sinusförmigen b) symmetrisch rechteckförmigen Spannung zusammen?
• Einer Wechselspannung von 230 V wird eine Gleichspannung von 100 V überlagert. Wie
hoch ist der Effektivwert?
• Die sinusförmige Spannung einer idealen Spannungsquelle wird mit einem kapazitiven
Teiler bestehend aus zwei Kondensatoren mit je 2 µF geteilt. Bilden Sie eine Ersatzquelle
für den Ausgang des Teilers. Wie groß ist der Ausgangswiderstand?
INSTITUT FÜR MIKROELEKTRONIK UND MIKROSENSORIK
JOHANNES KEPLER UNIVERSITÄT LINZ
Praktikum Elektrotechnik
WS 2013
Protokoll
Übung 2: Netzwerke und Drehstrom
Übungsdatum
Abgabedatum
Name
Name
Matr.Nr.
Matr.Nr.
Unterschrift
Unterschrift
56
KAPITEL 2. NETZWERKE UND DREHSTROM
57
Kapitel 3
Transformator
3.1 Theoretische Grundlagen des Transformators
3.1.1 Idealer Transformator
Transformatoren und Übertrager bestehen aus zwei oder mehreren Wicklungen (Spulen), die
magnetisch durch einen Eisenkern miteinander gekoppelt sind. Sie dienen zur Spannungs–,
Strom– und Widerstandsanpassung und –umformung, sowie zur Trennung von Stromkreisen
(galvanische Trennung).
Abbildung 3.1: Schematische Darstellung eines Transformators
In Abbildung 3.1 bezeichnet Φh den Hauptfluss, welchen die Ströme beider Spulen gemeinsam
aufbauen (im Nennbetrieb wirken die beiden Durchflutungen gegeneinander), Φ1σ und Φ2σ die
Streuflüsse der Primär- und Sekundärwicklung (jener Teil des Flusses der die jeweils andere
Spule nicht durchtritt). Als Streufluss bezeichnet man jenen Teil des Flusses, welcher nicht zur
Energieübertragung beiträgt und sich außerhalb des Eisenkerns schließt. Mit N1 und N2 werden
die Windungszahlen der beiden Wicklungen bezeichnet.
Beim idealen (das heißt verlustlosen) Transformator ist die aufgenommene Leistung gleich der
abgegebenen Leistung. Der reale Transformator verursacht dagegen Verluste, die in der Wicklung und im Kern entstehen.
KAPITEL 3. TRANSFORMATOR
58
Die Grundlage des Transformators bildet das Induktionsgesetz
u(t) = N
dΦ
.
dt
(3.1)
Damit ergeben sich Primär- und Sekundärspannung zu
dΦh
dt
dΦh
uh2 (t) = N2
.
dt
uh1 (t) = N1
(3.2)
Daraus folgt unmittelbar das Spannungsübersetzungsverhältnis
ü=
uh1 N1
=
.
uh2 N2
(3.3)
3.1.2 Ersatzschaltbild des realen Transformators
Herleitung
Für die Primärseite (u1 ) und die Sekundärseite (u2 ) gelten mit den ohmschen Widerständen der
Primär- bzw. Sekundärwicklung (R1 , R2 )
dΦ1
dt
dΦ2
u2 = i2 R2 + N2
dt
u1 = i1 R1 + N1
(3.4)
wobei sich die Gesamtflüsse Φ1 und Φ2 zu
Φ1 = Φh + Φ1σ
Φ2 = Φh + Φ2σ
und
(3.5)
ergeben. Mit den Gleichungen
Φ=
"
s
!
!B d!A
! d!s = i N
H
(3.6)
und
!B = µ H
!
ergibt sich der Hauptfluss zu
Φh =
1
Rm, Fe
(i1 N1 + i2 N2 ) ,
mit Rm, Fe =
lFe
µAFe
(3.7)
und die Streuflüsse zu
A1,Lu
i1 N1
l1,Lu
A2,Lu
Φ2σ = µ0
i2 N2 .
l2,Lu
Φ1σ = µ0
(3.8)
3.1. THEORETISCHE GRUNDLAGEN DES TRANSFORMATORS
59
In Gleichung (3.7) bezeichnet AFe den Querschnitt und lFe die mittlere Länge des Eisenkerns.
ALu und lLu der Gleichungen (3.8) bezeichnen die mittleren Querschnitte und Längen der Streupfade, wobei der Eisenpfad aufgrund des kleinen magnetischen Widerstandes im Vergleich zu
Luftpfaden vernachlässigt wird.
Die Wicklungen besitzen daher die Streuinduktivitäten
A1,Lu
l1,Lu
A2,Lu
L2σ = N22 µ0
l2,Lu
(3.9)
AFe
lFe
A
Fe
L2h = N22 µ
lFe
(3.10)
L1σ = N12 µ0
und die Hauptinduktivitäten
L1h = N12 µ
sowie eine gemeinsame Gegeninduktivität
AFe
.
lFe
Die Spannungsgleichungen (3.4) gehen somit über in
M = N1 N2 µ
di1
di1
di2
+ L1h
+M
dt
dt
dt
di2
di2
di1
u2 = i2 R2 + L2σ
+ L2h
+M
.
dt
dt
dt
u1 = i1 R1 + L1σ
(3.11)
(3.12)
Zur einfacheren Darstellung der Verhältnisse ist es üblich, beide Gleichungen auf die Windungszahlen der Primärseite zu beziehen. Die auf die Primärseite umgerechneten Sekundärgrößen
werden mit (- ) bezeichnet und lauten daher
N2- = N1 = N2 ü
u-2 = u2 ü
u-2 i-2 = u2 i2
2
i-2
2 R2 = i 2 R2
L-2σ = L2σ ü2
⇒
⇒
L-2h = L2h ü2 = N22 µ
1
ü
R2 = R2 ü 2
i-2 = i2
(3.13)
A N12
2 A
=
N
µ = L1h .
1
l N22
l
Erweitert man in den Spannungsgleichungen (3.12) die sekundärseitigen Größen folgendermaßen mit dem Übersetzungsverhältnis
d i2
di1
di1
+ L1h
+ Mü ü
dt
dt
dt
i2
i2
d
d
di1
i2
u2 ü = R2 ü2 + L2σ ü2 ü + L2h ü2 ü + Mü
ü
dt
dt
dt
u1 = i1 R1 + L1σ
(3.14)
KAPITEL 3. TRANSFORMATOR
60
und beachtet
AFe N1
AFe
= N12 µ
= L1h
lFe N2
lFe
= L1h
Mü = N1 N2 µ
2
L2h ü =
L-2h
und
(3.15)
so erhält man
"
#
di1 di-2
di1
+ L1h
+
u1 = i1 R1 + L1σ
dt
dt
dt
"
#
di1 di-2
- - di2
+ L1h
+
u2 = i2 R2 + L2σ
.
dt
dt
dt
(3.16)
Der Übergang von den Augenblickswerten mit Hilfe der komplexen Schreibweise auf die komplexen Zeiger ergibt
u(t) = Re (U(t))
i(t) = Re (I(t))
ωL = X .
mit U(t) = Ũ e jωt
˜ jωt
mit I(t) = Ie
(3.17)
Eingesetzt in (3.16) erhält man daraus
,
Ũ1 = I˜1 R1 + jX1σ I˜1 + jXh I˜1 + I˜2,
- ˜I2 + jXh I˜1 + I˜2- .
Ũ2- = I˜2- R-2 + jX2σ
(3.18)
Wenn man noch zusätzlich die Eisenverluste VFe durch einen Verlustwiderstand RFe berücksichtigt, ergibt sich die Ersatzschaltung nach Abbildung 3.3. Ein idealer Transformator ohne
Verluste und ohne Streufelder kann durch ein Ersatzschaltbild, wie es in Abbildung 3.2 dargestellt ist, beschrieben werden. Da die Hauptinduktivitäten L1h und L-2h gleich groß sind, können
Abbildung 3.2: Ersatzschaltbild eines verlustlosen Transformators ohne Streufeld
Primär- und Sekundärwicklung im Ersatzschaltbild durch eine einzige Reaktanz Xh = ωL1h
berücksichtigt und Primär- und Sekundärkreis miteinander verbunden werden. Dabei müssen
die sekundärseitigen Größen mit dem Übersetzungsverhältnis auf die Primärseite umgerechnet
werden. Die Eisenverluste werden durch einen Wirkstrom I˜Fe durch RFe parallel zum Blindstrom (Magnetisierungsstrom), I˜m durch die Hauptreaktanz Xh modelliert. Die Streuinduktivitä- dargestellt. Die Kupferverluste
ten L1σ und L-2σ werden durch die Streureaktanzen X1σ und X2σ
in Primär- und Sekundärspule werden durch die Widerstände R1 und R2 repräsentiert.
3.1. THEORETISCHE GRUNDLAGEN DES TRANSFORMATORS
61
Abbildung 3.3: Ersatzschaltbild des realen Transformators
Eisenverluste
Die Eisenverluste setzen sich aus Hysterese- und Wirbelstromverlusten zusammen.
VFe = VHy +VW
(3.19)
Die Hystereseverluste entstehen im Eisenkern durch die andauernde Ummagnetisierung infolge
der angelegten Wechselspannung. Sie sind proportional der Frequenz der Wechselspannung und
der Fläche der Hysteresekurve. Aus diesem Grund werden spezielle Trafobleche mit möglichst
schmaler Hystereseschleife (magnetisch weiches Material) verwendet.
Die Wirbelstromverluste entstehen im Eisenkern, der wie eine geschlossene Wicklung wirkt.
Die Ausbreitung der Wirbelströme kann durch Lamellierung des Eisenkerns oder durch Verwendung gesinterter Pulverkerne reduziert werden. Die Wirbelstromverluste sind proportional
f 2 B2 .
Kupferverluste
Die Kupferverluste sind die ohmschen Verluste der beiden Wicklungen, die im Ersatzschaltbild
durch R1 und R-2 berücksichtigt sind. Sie ergeben sich zu
VCu = I12R1 + I22 R2
(3.20)
Es ist zu beachten, dass die Kupferverluste immer für die Betriebstemperatur der Wicklungen
(75◦ C) angegeben werden. Im kalten Zustand (ϑ) gemessene Werte sind daher auf Betriebstemperatur umzurechnen.
"
#
75◦ − ϑ
75◦
ϑ
VCu = VCu 1 +
(3.21)
235◦ + ϑ
Leerlauf– und Kurzschlussversuch
Mit diesen beiden Versuchen lassen sich die Größen im Ersatzschaltbild (näherungsweise) bestimmen.
Die im Leerlauf vom Transformator aufgenommene Verlustleistung PL wird zum überwiegenden Teil von den Eisenverlusten bestimmt, da die Kupferverluste wegen der geringen Stromaufnahme vernachlässigbar sind. Die Leerlaufleistung PL kann den Eisenverlusten VFe gleichgesetzt
KAPITEL 3. TRANSFORMATOR
62
werden. Weiters sind die Streuinduktivitäten typischerweise wesentlich kleiner als die Hauptinduktivität, weshalb die Hauptreaktanz der Primärreaktanz näherungsweise gleichgesetzt werden
kann.
Im Kurzschlussfall ist nur eine geringe Spannung erforderlich, um große Ströme im Transformator zu treiben. Es wird deshalb eine wesentlich kleinere Hystereseschleife durchlaufen und
die Eisenverluste sind damit sehr klein. Die Kurzschlussleistung PK ergibt sich daher zu
PK = I12R1 + I22 R2 = VCu .
(3.22)
Für die Streuinduktivitäten gilt meist L1σ ≈ L-2σ = L2σ ü2 .
Schaltzeichen
Abbildung 3.4 zeigt das Schaltzeichen eines einphasigen Transformators.
Abbildung 3.4: Schaltzeichen eines Transformators mit zwei getrennten Wicklungen
3.2. ÜBUNGSDURCHFÜHRUNG
63
Abbildung 3.5: Aufgeschnittener Drehstromtrafo. Auf jedem Schenkel des Eisenkerns sitzt je
eine Primär– und eine Sekundärwicklung. Zur Kühlung ist der Trafo in einem ölgefüllten Gehäuse eingebaut. Quelle: Wikipedia
3.2 Übungsdurchführung
3.2.1 Bestimmen des Transformator–Ersatzschaltbildes
Auf ihrem Steckbrett steht ihnen ein kleiner Trafo in einem PVC–Gehäuse zur Verfügung. Der
Trafo hat zwei Wicklungen die an den Pins herausgeführt sind. Diesen Trafo sollen Sie charakterisieren. Bestimmen Sie dazu zunächst die Kupferwiderstände mit einem Multimeter.
Leerlaufversuch
Ermitteln Sie das Spannungsübersetzungsverhältnis des Transformators, indem Sie den Trafo
auf der Primärseite mit Û1 = 8 V (Scheitelwert), 1 kHz (fix) aus dem Funktionsgenerator speisen
und auf der Sekundärseite die Leerlaufspannung messen (mit Multimeter). Oszillographieren
Sie anschließend Strom und Spannung auf der Primärseite des leerlaufenden Trafos und messen
Sie so U1 und I1 , sowie deren Phasenverschiebung ϕ. Verwenden Sie zur Strommessung einen
Shunt von 10 Ω nach Abbildung 1.25 (Seite 32). Beachten Sie, dass Sie bei der Phasenmessung
durch die gemeinsame Masse der Oszilloskopeingänge die Shuntspannung invertieren müssen,
um die richtige Phase zu erhalten. Verwenden Sie für diese Messung folgenden Tabellenkopf:
Û1 ÛS U1
V V V
I1 U2
mA V
ϕ cos ϕ
S1
P1
mVA mW
KAPITEL 3. TRANSFORMATOR
64
Dabei ist ÛS die Spannungsamplitude, die Sie am Shunt messen, S1 = U1 I1 die Scheinleistung
und P1 die Wirkleistung, die der Trafo aufnimmt und die den Eisenverlusten VFe entspricht.
Zeichnen Sie für einen beliebigen Betriebsfall (U1 > 0) den zeitlichen Verlauf von U1 (t), I1 (t),
P1 und B(t) für 2 Perioden in ein gemeinsames Diagramm.
Kurzschlussversuch
Hier wird der Ausgang des Trafos kurzgeschlossen und dann die Eingangsspannung so eingestellt, dass sich als primärseitig aufgenommene Ströme folgende Werte ergeben: Iˆ1 = 4 mA,
8 mA, 15 mA, 30 mA und 50 mA. Zu messen, berechnen bzw. zu oszillographieren sind folgende Größen:
Û1 ÛS U1
V V V
I1 ϕ
mA
cos ϕ
◦
75
S1
P1 VCu
mVA mW mW
◦
75 = f(I ). Vergleichen Sie die Werte von R und
Zeichnen Sie aus den berechneten Größen VCu
1
1
R2 mit denen die Sie mit dem Multimeter erhalten haben.
Auswertung
Bestimmen Sie nun aus den gewonnenen Daten die Parameter des Ersatzschaltbildes. Entsprechen die Werte Ihren Erwartungen? Wie groß ist der Ausgangswiderstand des Trafos, wenn Sie
ihn als Quelle betrachten? (Hinweis: Dieser hängt nicht nur vom Trafo ab!)
In welchem Betriebszustand weist der Trafo
• die geringsten absoluten Verluste
• den besten Wirkungsgrad
auf? Kommentieren Sie ihre Überlegungen.
Überprüfen Sie anhand des folgenden Belastungsversuchs, ob der Trafo das von Ihnen prognostizierte Quellen–Verhalten zeigt (vergleichen Sie die gemessenen Werte von U2 mit den
berechneten). Kommentieren Sie das Ergebnis Ihrer Untersuchung.
Belastungsversuch
Belasten Sie die Sekundärseite des Trafos mit den Lastwiderständen RL = 10 kΩ, 4,7 kΩ, 2 kΩ,
1 kΩ, 680 Ω, 330 Ω, 220 Ω, 150 Ω, 100 Ω, 55 Ω, 33 Ω und 0 Ω und messen bzw. berechnen
Sie die Größen für die nachstehende Tabelle. Der Wirkungsgrad η ergibt sich aus η = P2 /P1 .
Kontrollieren Sie vor jeder Messung die Eingangsspannung des Transformators und stellen Sie
Û1 = 6 V ein.
Zeichnen Sie aus den berechneten Größen die Diagramme P2 = f(P1 ), cos ϕ = f(P1 ) und η =
f(P1 ).
Û1 ÛS U1
V V V
I1 U2
mA V
ϕ cos ϕ
S1
P1
mVA mW
P2
η
mW %
3.2. ÜBUNGSDURCHFÜHRUNG
65
3.2.2 Eigenbau–Trafo
Bauen sie nun aus zwei Spulen und den beiden Kernhälften einen Transformator. Die Windungszahlen werden ihnen vom Übungsleiter mitgeteilt.
Hinweis: Achten sie beim Zusammenbau darauf, dass die beiden Kernhälften frei von Verunreinigungen sind und der der Kern ordentlich geschlossen ist. Stecken sie einen kleinen Brückenverbinder unter dem Kern in das Steckbrett. Dadurch wird der Kern etwas angehoben und ein
unerwünschter Luftspalt vermieden.
Trafo ohne Luftspalt
Bestimmen Sie wiederum die Parameter des Ersatzschaltbildes dieses Trafos. Dokumentieren
Sie die Messungen in geeigneter Weise (wie bei voriger Aufgabe).
Stellen Sie einmal die Frequenz der Quelle auf einen möglichst geringen Wert und versuchen
Sie dann, die obere Kernhälfte aus dem Trafo zu ziehen. Wiederholen Sie den Versuch mit einer
anderen Primärwindungsanzahl und dokumentieren (und begründen) Sie Ihre Beobachtung.
Trafo mit Luftspalt
Fügen sie nun in den Magnetkreis des Trafos einen Luftspalt ein. Vom Übungsleiter erhalten sie dazu einen speziellen selbstklebenden Luftspalt zum Applizieren zwischen den beiden
Kernhälften. (Nach der Übung ist der Luftspalt gemeinsam mit den Kopien ihrer Mitschrift abzugeben!) Wiederholen sie nun die Messungen für den Trafo mit geändertem Magnetkreis und
vergleichen sie die Ergebnisse mit denen ohne Luftspalt. Kommentieren sie die Unterschiede (und die Auswirkung des Luftspaltes) im Protokoll und berechnen sie aus den gemessenen
Werten die Dicke des Luftspaltes. (Hinweis: Für die Berechnung benötigen Sie den Eisenquerschnitt!)
Überlegen Sie, welche Vor- bzw. Nachteile ein Trafo mit Luftspalt hat und welche Anwendung
für einen solchen Trafo geeignet ist.
KAPITEL 3. TRANSFORMATOR
66
3.3 Fragen
Die Fragen dienen der Vorbereitung auf das Praktikum und stellen nicht notwendigerweise Prüfungsfragen dar. Nicht alle Fragen können ausschließlich mit den Informationen aus dem Skriptum beantwortet werden. Recherchieren sie selbstständig und diskutieren sie mit Kollegen!
• Ist Kupfer ein Kalt– oder Heissleiter?
• Was bedeutet ‘galvanische Trennung’?
• Zeichnen sie das Trafo–Ersatzschaltbild und benennen sie die Komponenten.
• Leiten sie den formellen Zusammenhang zwischen Windungszahlen und Übersetzungsverhältnis her.
• Wodurch entstehen in einem Trafo Verluste und mit welchen konstruktiven Maßnahmen
kann man diese minimieren?
• Überlegen sie, wie man bei einem Schweißtrafo den Ausgangsstrom (bei Schweißbetrieb
= im Kurzschlussfall) verstellen könnte ohne dabei eine hohe Verlustleistung in Kauf
nehmen zu müssen.
• Oft hört man Transformatoren brummen. Woran liegt das? Welcher physikalische Effekt
verursacht das Geräusch und welche Frequenz hat der Brummton?
• Ihr Onkel aus Japan hat ihnen völlig blauäugig an Stelle eines Radios/Videos/TV einen
Jodelautomaten geschenkt, der nur mit 110 Volt Netzspannung betrieben werden kann.
Sie haben einen 1:1 Trafo für den Betrieb an 230 Volt. Können sie mit diesem (ohne den
Trafo zu verändern) eine Spannung von 110 Volt erreichen? Wenn ja, wie?
• Zeichnen sie für einen Trafo im Leerlauf/Kurzschluss den Verlauf von Fluss / Primärstrom
/ Sekundärspannung bei sinusförmiger Primärspannung.
• Modellieren Sie den Magnetkreis eines Trafos mit magn. Spannungsquellen und magn.
Widerständen.
INSTITUT FÜR MIKROELEKTRONIK UND MIKROSENSORIK
JOHANNES KEPLER UNIVERSITÄT LINZ
Praktikum Elektrotechnik
WS 2013
Protokoll
Übung 3: Transformator
Übungsdatum
Abgabedatum
Name
Name
Matr.Nr.
Matr.Nr.
Unterschrift
Unterschrift
68
KAPITEL 3. TRANSFORMATOR
69
Kapitel 4
Filter und Schwingkreise
4.1 Allgemeines
4.1.1 Dämpfungsmaß und Bodediagramm
Das Dämpfungsmaß a ist das logarithmische Verhältnis von Eingangsleistung zu Ausgangsleistung einer elektronischen Schaltung. Seine Maßeinheit ist das Dezibel (dB).
" #
P1
a = 10 log
(4.1)
P2
Ist der Bezugswiderstand, in dem die Leistung umgesetzt wird, für Eingang und Ausgang gleich,
so kann das Leistungsverhältnis in ein Spannungs- oder Stromverhältnis umgewandelt werden
(P = U 2 /R = I 2 R) und es ergibt sich mit Hilfe der Rechenregeln für Logarithmen:
"
#
|U1 |
a = 20 log
und
(4.2)
|U2 |
" #
|I1 |
(4.3)
a = 20 log
|I2 |
Häufig wird auch der Betrag des komplexen Übertragungsverhältnisses ü = uuae in Dezibel angegeben (20 log (|ü|)). Ein Diagramm, in dem sowohl der Logarithmus des Betrags (in dB) als
auch die Phase des Übertragungsverhältnisses über dem Logarithmus der Frequenz dargestellt
ist, heißt Bodediagramm. Abbildung 4.1 zeigt ein solches Bodediagramm für den einfachen Fall
eines RC-Tiefpasses (Abbildung 4.2).
4.1.2 Bandbreite und Grenzfrequenz
Der Kurvenverlauf im Bodediagramm wird oft durch Geradenstücke angenähert. In Abbildung 4.1 a) kann also der Teil links von fg durch eine waagrechte Gerade und der Teil rechts
von fg durch eine Gerade mit der Steigung −1 ersetzt werden, wenn 20 dB durch dieselbe Länge repräsentiert werden wie eine Dekade der Frequenz (U2 nimmt mit 20 dB/Dekade ab). Diese
beiden Geraden schneiden sich genau bei fg .
√
fg ist jene Frequenz, bei der die Ausgangsspannung U2 auf den 1/ 2-fachen Wert der maximalen Ausgangsspannung abgesunken ist (−3 dB-Punkt), sie heißt Grenzfrequenz. Bei der
70
KAPITEL 4. FILTER UND SCHWINGKREISE
Abbildung 4.1: Bodediagramm eines RC-Tiefpasses
Grenzfrequenz ist die Ausgangsleistung die Hälfte der maximalen Ausgangsleistung und beim
RC-Glied eilt die Ausgangsspannung der Eingangsspannung um exakt 45◦ nach.
Bei Schaltungen, deren Ausgangsgröße (Strom oder Spannung) ein Maximum besitzt, treten
zwei Grenzfrequenzen√fgo und fgu oberhalb und unterhalb des Maximums auf, bei denen die
Ausgangsgröße um 1/ 2 abgesunken ist. Die Differenz zwischen fgo und fgu heißt Bandbreite
B.
B = fgo − fgu
(4.4)
4.2 Filter
Filter sind aus passiven und aktiven oder nur aus passiven Elementen aufgebaute Netzwerke, deren Übertragungsverhalten frequenzabhängig ist und deutlich getrennte Durchlass- und
Sperrbereiche besitzt. Bei Filtern unterscheidet man je nach Lage der Grenzfrequenzen vier
Grundtypen: Tiefpass, Hochpass, Bandpass und Bandsperre.
Tiefpass
Tiefpässe haben die Aufgabe, unerwünschte Frequenzen eines Spektrums, wie sie z. B. bei der
Modulation, Demodulation, Gleichrichtung, Verstärkung entstehen, oberhalb einer bestimmten
Grenzfrequenz zu unterdrücken.
Hochpass
Im Gegensatz zum Tiefpass soll der Hochpass Frequenzen oberhalb der Grenzfrequenz möglichst ohne Dämpfung übertragen und unterhalb sperren.
4.3. SCHWINGKREISE
71
Bandpass
Aufgabe des Bandpasses ist es, nur ein ganz bestimmtes Frequenzband passieren zu lassen
(Durchlassbereich) und alle anderen Frequenzen zu sperren. Bandpässe werden z. B. in Empfängern eingesetzt, um unerwünschte von erwünschten Frequenzen zu trennen, oder in Sendern,
um störende Modulationsprodukte von der Antenne fernzuhalten.
Bandsperre
Die Bandsperre ist das „Gegenteil“ vom Bandpass, d. h. sie sperrt ein definiertes Frequenzband
und lässt alle anderen Frequenzen passieren.
4.3 Schwingkreise
Die Theorie zu den Schwingkreisen ist in den Vorlesungsskripten zu Elektrotechnik nachzulesen.
4.3.1 Parallelschwingkreis
Der Parallelschwingkreis ist eine frequenzabhängige Schaltung, bestehend aus einem Widerstand, einer Induktivität und einer Kapazität, die parallel geschaltet sind. Wird eine Wechselspannung an den Schwingkreis gelegt, so gerät dieser bei einer bestimmten Frequenz in Resonanz. Diese Resonanzfrequenz ist abhängig von der Kapazität und der Induktivität.
1
ωR = √
LC
(4.5)
Im Resonanzfall hat der Parallelschwingkreis seinen größten Widerstand. Das bedeutet, dass der
Gesamtstrom ein Minimum wird. In der Induktivität bzw. Kapazität können Ströme auftreten,
die erheblich höher als der Gesamtstrom sind, sich aber durch ihre entgegengesetzte Phasenlage
kompensieren („Stromüberhöhung“).
Das Verhältnis vom Spulenstrom bzw. Kondensatorstrom zum Gesamtstrom bei der Resonanzfrequenz wird als Gütefaktor oder Güte Q p bezeichnet.
/
.
C
|IL | ..
=R
Qp =
.
|I| ω=ωR
L
(4.6)
Der Kehrwert der Güte ist der Verlustfaktor oder die Dämpfung d 1 . Die Bandbreite B des Parallelschwingkreises bestimmt sich aus jenen beiden Frequenzen, an denen die Spannung am
Schwingkreis auf den √1 -fachen Wert der Spannung bei Resonanzfrequenz abgesunken ist,
2
wenn der Schwingkreis mit einer idealen Stromquelle angespeist wird.
B=
1 Achtung,
ωR
1
=
.
RC Q p
(4.7)
verwechseln Sie die Dämpfung d eines Schwingkreises nicht mit dem in Abschnitt 4.1.1 eingeführten Dämpfungsmaß!
KAPITEL 4. FILTER UND SCHWINGKREISE
72
4.3.2 Serienschwingkreis
Der Serienschwingkreis stellt die zum Parallelschwingkreis duale Schaltung dar, bei welcher
Widerstand, Induktivität und Kapazität in Serie geschaltet sind. Die Resonanzfrequenz berechnet sich genauso wie beim Parallelschwingkreis, jedoch hat der Serienschwingkreis bei der
Resonanzfrequenz seinen kleinsten Widerstand. Das bedeutet, dass der Gesamtstrom ein Maximum wird. An der Induktivität bzw. Kapazität können Spannungen auftreten, die erheblich
höher als die Gesamtspannung sind, sich aber durch ihre entgegengesetzte Phasenlage kompensieren („Spannungsüberhöhung“).
Entsprechend der Dualität von Serien- und Parallelschwingkreis ergibt sich für die Güte
/
1 L
Qs =
(4.8)
R C
und für die Bandbreite
B=
R ωR
=
.
L
Qs
(4.9)
4.4 Übungsdurchführung
• Bei allen Messungen ist darauf zu achten, dass die Eingangsspannung konstant ist. Im
Allgemeinen ist daher wegen des endlichen Innenwiderstandes des Generators nach jeder Frequenzänderung die Eingangsspannung nachzuregeln! Sollte der Aussteuerbereich
nicht ausreichen, müssen sie dies in der Auswertung der Ergebnisse berücksichtigen!
• Verwenden Sie zur Messung der Wechselspannungen entweder das Multimeter vom Typ
MX 47 (Dieses Messgerät ermöglicht die Messung von Wechselspannungen und Wechselströmen bis 20 kHz) oder die Messfunktion des Oszilloskops (MEASURE PEAK bzw.
EFFEKTIV).
• Achten Sie auf den Unterschied zwischen Spitzenwert und Effektivwert.
• Messen Sie bei allen Messaufgaben im Bereich starker Änderungen der Ausgangsspannung zusätzliche Frequenzpunkte.
• Der vermessene Frequenzbereich sollte mindestens die Dekade unter und die über der
Eckfrequenz bzw. Resonanzfrequenz erfassen.
4.4.1 Tiefpass
Bauen sie einen Tiefpass entsprechend Abbildung 4.2 auf. Vom Übungsleiter werden ihnen
entweder die Werte für R und C oder die erforderliche Grenzfrequenz bekanntgegeben (Wählen
sie eine geeignete Bauteilkombination aus den zur Verfügung stehenden Bauteilen aus).
Ermitteln sie anschließend das Bode–Diagramm des Tiefpasses indem sie das Übertragungsverhalten an mindestens 10 verschiedenen Frequenzen messen. Wählen sie dazu eine geeignete
Verteilung der Messpunkte.
Bestimmen sie die Grenzfrequenz des Tiefpasses rechnerisch aus den Bauteilwerten und grafisch aus dem Diagramm. Vergleichen Sie beide Ergebnisse.
4.4. ÜBUNGSDURCHFÜHRUNG
73
R
ue
ua
C
Abbildung 4.2: RC–Tiefpass
4.4.2 Serienschwingkreis
Bauen sie einen Schwingkreis entsprechend Abbildung 4.3 auf und nehmen sie das Bode–
Diagramm auf (mindestens 10 Messpunkte). Die Werte für R, C und L werden ihnen vom
Übungsleiter bekanntgegeben.
Dokumentieren sie neben Ûe, Ûa und ϕ auch die Spannungen ÛC und ÛL ! Die Spannungen
Ûe und Ûa , die Frequenzen und der Phasenwinkel ϕ = ϕua − ϕue sind mit dem Oszilloskop zu
messen (Achten Sie auf die gemeinsame Masse!). Die Spannungen UC und UL sind mit dem
Multimeter zu messen und in Spitzenwerte umzurechnen.
R
C uC
ue
ua
L
uL
Abbildung 4.3: Serienschwingkreis
Bestimmen Sie die Resonanzfrequenz des Serienschwingkreises rechnerisch aus den Bauteilwerten und grafisch aus dem Diagramm. Vergleichen Sie die Ergebnisse. Ermitteln Sie weiters
grafisch die Bandbreite des Schwingkreises.
4.4.3 Bandpass
Bauen sie einen Bandpass entsprechend Abbildung 4.4 auf. Die Bauteilwerte werden ihnen wieder vom Betreuer bekanntgegeben. Ermitteln sie anschließend das Bode–Diagramm der Schaltung indem sie das Übertragungsverhalten an mindestens 15 verschiedenen Frequenzen messen.
Wählen sie dazu eine geeignete Verteilung der Messpunkte.
Bestimmen Sie die Grenzfrequenzen des Bandpasses rechnerisch aus den Bauteilwerten und
grafisch aus dem Diagramm. Vergleichen Sie die Ergebnisse.
KAPITEL 4. FILTER UND SCHWINGKREISE
74
C1
ue
L1
C2
L2
R
ua
Abbildung 4.4: Bandpass
4.5 Fragen
Die Fragen dienen der Vorbereitung auf das Praktikum und stellen nicht notwendigerweise Prüfungsfragen dar. Nicht alle Fragen können ausschließlich mit den Informationen aus dem Skriptum beantwortet werden. Recherchieren sie selbstständig und diskutieren sie mit Kollegen!
• Warum wird für die Beschreibung von Grenzfrequenzen die -3 dB – Marke verwendet?
• Wie groß ist der Widerstand eines verlustlosen a) Serienschwingkreises b) Parallelschwingkreises im Resonanzfall?
• Leiten sie die Resonanzfrequenz eines LC–Parallelschwingkreises als Funktion der Windungszahl der zylindrischen Luftspule her.
• Warum haben zwei räumlich getrennte Spulen mit je 100 Windungen bei Serienschaltung
eine geringere Induktivität als eine Spule mit 200 Windungen? Notieren sie den formellen
Zusammenhang und finden sie eine phyikalische Begründung.
• Sie haben einen RC–Tiefpass erster Ordnung als integriertes Bauteil mit 3 Anschlüssen
zu Hand, benötigen aber einen Hochpass mit gleicher Resonanzfrequenz. Können sie das
Bauteil gebrauchen? Wenn ja, welche Anpassung müssen sie vornehmen um aus dem
Tiefpass einen Hochpass zu machen?
• Für eine Schaltung benötigen sie eine Spule mit einer Induktivität von 245 mH. Ihr Lieferant bieten aber nur Werte von 100 mH und 500 mH an. Welche Möglichkeiten gibt es
den gewünschten Wert zu erhalten?
INSTITUT FÜR MIKROELEKTRONIK UND MIKROSENSORIK
JOHANNES KEPLER UNIVERSITÄT LINZ
Praktikum Elektrotechnik
WS 2013
Protokoll
Übung 4: Filter und Schwingkreise
Übungsdatum
Abgabedatum
Name
Name
Matr.Nr.
Matr.Nr.
Unterschrift
Unterschrift