Übungsblatt 7

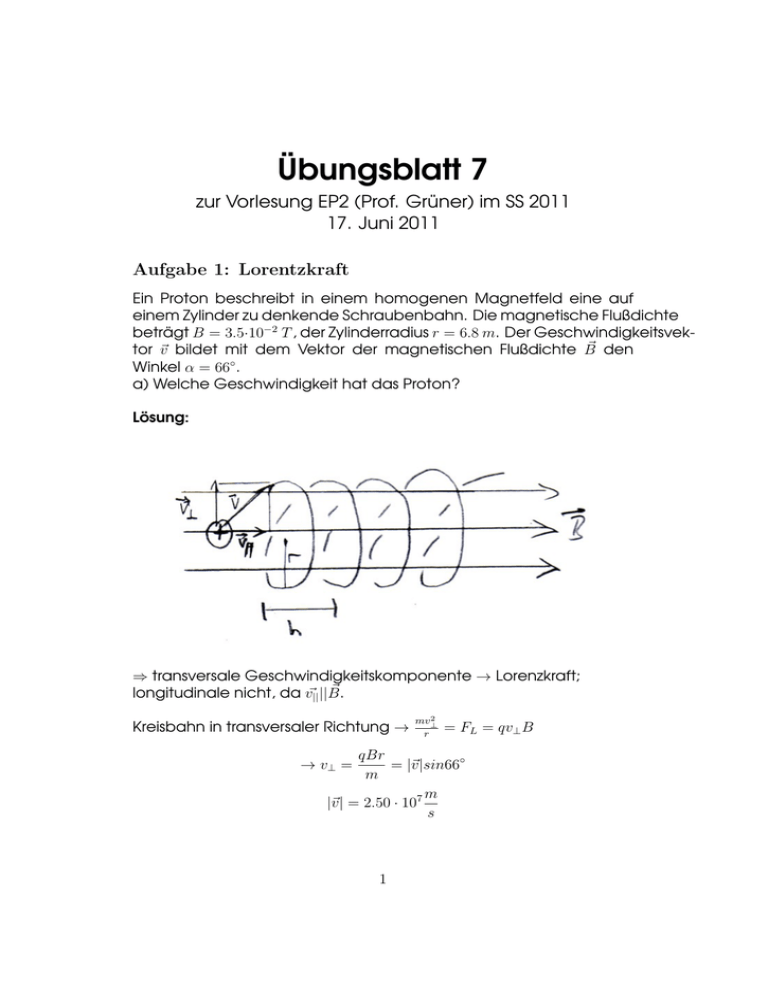
Übungsblatt 7
zur Vorlesung EP2 (Prof. Grüner) im SS 2011
17. Juni 2011
Aufgabe 1: Lorentzkraft
Ein Proton beschreibt in einem homogenen Magnetfeld eine auf
einem Zylinder zu denkende Schraubenbahn. Die magnetische Flußdichte
beträgt B = 3.5·10−2 T , der Zylinderradius r = 6.8 m. Der Geschwindigkeitsvek~ den
tor ~v bildet mit dem Vektor der magnetischen Flußdichte B
◦
Winkel α = 66 .
a) Welche Geschwindigkeit hat das Proton?
Lösung:
⇒ transversale Geschwindigkeitskomponente → Lorenzkraft;
~
longitudinale nicht, da v~|| ||B.
Kreisbahn in transversaler Richtung →
2
mv⊥
r
= FL = qv⊥ B
qBr
= |~v |sin66◦
m
m
|~v | = 2.50 · 107
s
→ v⊥ =
1
b) Welche Geschwindigkeitskomponente vk hat das Proton in Feldrichtung und welche Geschwindigkeitskomponente v⊥ hat es senkrecht
dazu?
v⊥ = 2.28 · 107
m
s
v|| = |~v | · cos66◦ = 1.02 · 107
m
s
Aufgabe 2: Hall-Effekt
Eine Kupferfolie (d = 10−5 m) wird von einem Strom der Stärke 10 A
durchflossen. Im Magnetfeld B = 0.42 T wird die Hallspannung UH =
2.2 · 10−5 V gemessen. Berechnen Sie die Hall-Konstante von Kupfer
und die Dichte n der Elektronen. Berechnen Sie daraus die Anzahl
der freien Elektronen in 1 mol Kupfer und vergleichen Sie diese Zahl
mit der Avogadro-Konstante (NA = 6.022 · 1023 ).
Lösung:
I~ = nq · v~D · b · d
FL = FC
~ = nq UH
nq · v~D · B
b
~
~
I~B
UH
1 I~B
= nq
→ UH =
·
bd
b
nq d
1
mit
= RH →
nq
2
RH =
m3
UH d
2.2 · 10−5 V · 10−5 m
=
= 5.24 · 10−11
~
10A · 0.42T
C
I~B
1
= 1.2 · 1029 m−3
n=
qRH
Molmasse Mmol Cu: 63.546g,
Dichte ρCu : 8.92 cmg 3 (bei 20◦ ).
mol
= 7.12cm3 .
V1mol = MρCu
ne− ,1mol = 7.12cm3 · 1.2 · 1023 cm−3 = 8.5 · 1023
ne− ,1mol
= 1.43 → im Schnitt tragen 1.43 e− pro Atom zum Ladungsstrom bei.
NA
Aufgabe 3: Massenspektrometer
Positive Ionen verschiedener Geschwindigkeiten und Massen, jedoch
gleicher Ladung q treten bei P0 senkrecht in die homogenen, senkrecht
gekreuzten Felder der elektrischen Feldstärke E0 und der magnetischen Flussdichte B0 ein. Ein Teil der Ionen durchläuft die Anordnung
3
geradlinig und gelangt durch die Blende R in das homogene magnetische Feld der Flussdichte B1 . Dort werden die Teilchen abgelenkt und treffen zwischen P1 und P2 auf einem Registrierschirm auf.
Es ist E0 = 250 V /m, B0 = 10−3 T , B1 = 1 T , q = 1.6 · 10−19 C.
a) Wie groß ist der Betrag der Geschwindigkeit der Teilchen, welche
die gekreuzten Felder geradlinig durchlaufen und bei R austreten?
Auf welcher Seite der Blende R treffen Teilchen mit kleinerer Geschwindigkeit
auf? Begründen Sie die Antwort.
Lösung:
FC = FL
E0
m
= 2.5 · 105
qE0 = qvB0 → v =
250V
s
B0 = 10−3 T m
v kleiner → FL kleiner → linke Seite (rechts in Flugrichtung).
b) Berechnen Sie die spezifische Ladung mq der Ionen, die in P1 bzw.
P2 auf dem Schirm auftreffen (RP1 = 10 cm, RP2 = 20 cm). Bestimmen
Sie die zugehörigen Massen m1 und m2 .
Lösung:
q
v
mv 2
= qvB1 →
=
r
m
B1 r
2.5 · 105 ms
q
v
C
=
=
= 5 · 106
m1
B1 r1
1T · 0.05m
kg
q
C
= 2.5 · 106
m1 = 3.2 · 10−26 kg
m2
kg
m2 = 6.4 · 10−26 kg
"
Einheiten:
Am2
Cm2 s2
C
1
m2
Cm2
=
=
=
=
=
2
2
2
2
Ts
Vs
Js
Js
kgm s
kg
#
c) Nach Entfernen des Schirms gelangen die Ionen in ein homogenes elektrisches Feld der Feldstärke E = 105 V /m, in dem sie abgebremst werden. Berechnen Sie die Reichweite der in P1 bzw. P2 in
das elektrische Feld eintretenden Teilchen.
4
Lösung:
1 2
mv 2
mv = qE1 · s → s =
2
2qE1
s1 = 59.5m
s2 = 119m
5
"
kgm3
=m
s2 CV
#