10. Klasse

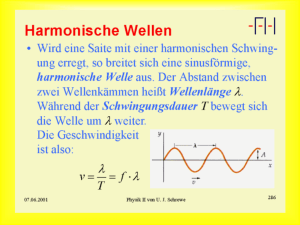
228
Grundwissen Physik
Jahrgangsstufe 10
Geozentrisches Weltbild Ein geometrisches Modell von Himmel und Er­
de verdanken wir den Griechen ab dem 7. Jahrhundert v. Chr. Sie erklärten
alle Bewegungen der Gestirne mithilfe von Kugelschalen um die Erde. ↑1
Himmelsmaterie war etwas völlig anderes als die vier Elemente Erde,
Wasser, Luft und Feuer des Erdbereichs.
Dass die Sonne viel weiter von der Erde entfernt ist als der Mond, bewies
Aristarchos von Samos um 260 v. Chr. Er fand heraus, dass die Sonne viel
größer als die Erde ist: Deshalb glaubte er, dass die Sonne im Zentrum der
Welt stehen müsse. Ptolemaios fasste die Astronomie im 2. Jahrhun­
dert n. Chr. in einem systematischen Handbuch, dem Almagest, zusammen.
Erde
Mond
Sonne
Sterne
1
Saturn
Jupiter
Sonne
Erde
Mars
2
T
T2
große
Halbachse
A2
Brennpunkte
∆t1 = ∆t2
2
a
3
1
1
dritten Potenzen der großen Halbachsen ihrer Bahnellipsen: ___
= ___
.
2
3
kleine
Halbachse
A1
Heliozentrisches Weltbild Kopernikus „stellte“ 1543 die Sonne in das
Zentrum der Welt, die Erde und alle Planeten umkreisen sie. ↑2
Galilei entdeckte mit dem neu entwickelten Fernrohr Mondgebirge, Ju­
pitermonde (nicht auf Kugelschalen), Venusphasen …
Kepler beschrieb zu Beginn des 17. Jahrhunderts die Planetenbewegun­
gen in drei mathematischen Gesetzen: ↑3
– Die Planeten umlaufen die Sonne auf Ellipsen. Jeweils ein Brennpunkt
dieser Ellipsen liegt in der Sonne.
– Die gedachte Verbindungslinie Sonne–Planet überstreicht in gleichen
Zeitspannen gleich große Flächen.
– Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die
A1 = A2
3
Erde
Mond
4
5
6
a2
Newton zeigte Ende des 17. Jahrhunderts, dass große Massen riesige Gra­
vitationskräfte ausüben, die Planeten und Monde auf ihren Bahnen halten. ↑4
Bewegungen auf der Erde und im Weltall können bei Kenntnis der Kräfte
(Wechselwirkungen) zwischen Körpern mithilfe der newtonschen Gesetze
erklärt werden: Trägheits­, Bewegungs­ und Wechselwirkungsgesetz.
Kosmologisches Weltbild Mithilfe der Spektralanalyse ↑5 von Fraun­
hofer (1814) erkannte man, dass es im Weltall die gleichen chemischen
Elemente gibt wie auf der Erde. Der Intensitätsverlauf der Strahlung von
Sternen enthält Informationen über die Temperaturen an ihrer Oberfläche.
Die Fixsternparallaxe wurde 1838 gefunden: Selbst die nächsten Fixsterne
sind 100 Billionen Kilometer entfernt.
Im 20. Jahrhundert hat die Astronomie von Einsteins Relativitätstheorien
sowie der neuen Atom­ und Kernphysik profitiert:
– Bei der Fusion von Wasserstoff zu Helium setzen Sterne gewaltige Ener­
gien frei. Sind rund 10 % des Wasserstoffs verbraucht, blähen sie sich auf,
explodieren und stoßen ihre Gashüllen ab. Dabei können Rote Riesen,
Weiße Zwerge, Schwarze Löcher … entstehen.
– Nach Einstein ist die Lichtgeschwindigkeit die höchste Geschwindigkeit
im Kosmos. Raum und Zeit hängen vom Beobachter, dem beobachteten
Körper und ihrer Bewegung ab. Die Krümmung von Raum und Zeit durch
Materie führt zu den gekrümmten Bahnen von Planeten und Licht. ↑6
– Es gibt Billionen von Galaxien.
– Das Universum hat sich wahrscheinlich aus einem Urknall vor rund
14 Milliarden Jahren entwickelt und dehnt sich noch weiter aus.
Licht
9783464853184 Inhalt_S228 228
25.08.2008 12:18:22 Uhr
229
Jahrgangsstufe 10
Bewegungen – iterativ berechnet Der Grundgedanke des iterativen Verfahrens ist, dass das Ergebnis eines Rechenschritts zur Eingabe für den
nächsten Rechenschritt wird. ↑7 Bei jedem Rechenschritt finden dieselben Operationen statt. Beispiele:
– Fall mit Luftwiderstand Die Kraft F auf den fallenden Körper setzt sich
aus der abwärts beschleunigenden Gewichtskraft FG und der bremsenden
Luftwiderstandskraft FL zusammen:
F = FG – FL mit FG = m · g und FL = ​ _12 ​cW · A · r · v2.
Da die Geschwindigkeit nach dem Start (aus der Ruhe) zunimmt, wird
die Luftwiderstandskraft zunächst größer und die Gesamtkraft F folglich kleiner. Wenn die Luftwiderstandskraft genauso groß ist wie die
Gewichtskraft, nimmt die Geschwindigkeit nicht weiter zu.
Die Veränderungen von Kraft, Geschwindigkeit und Ort werden iterativ
berechnet. ↑8 Die Diagramme zeigen bei längeren Fallzeiten den bremsenden Einfluss des Luftwiderstands im Vergleich zum freien Fall. ↑9 ↑10
1 ​  c · A · r · v 2
F0 = m · g – ​ __
0
2 W
F
v1 = v0 + ​ ___0 ​  · ∆t
m
1 ​  · (v + v ) · ∆t
x1 = x0 + ​ __
0
1
2
t1 = t0 + ∆t
v
in ms
1 ​ c · A · r · v 2
F1 = m · g – ​ __
1
2 W
…
10
mit Luftwiderstand
30
20
0
0
5
10
t in s
8 Rechenschritt (Fall mit Luftwiderstand) 9 t-v-Diagramm (∆t = 1 s)
– Harmonische Schwingungen Lineare rücktreibende Kräfte F = – k · x
bewirken harmonische Schwingungen. Die Bewegungsfunktionen sind
Sinus- und Kosinusfunktionen. ↑11 Allgemein gilt für die Periodendauer T harmonisch schwingender Pendel:
__
T = 2 π · ​ __
​ m ​ ​   .
k
___
Federpendel: T = 2π · ​ __
​ m ​  ​   (k = D)
D
__
m · g
Fadenpendel: T = 2π · ​ __
​ gl  ​ ​   (k = ​ _____
 ​ 
  für kleine Auslenkungen)
l
Die Frequenz f ist jeweils gleich dem Kehrwert der Periodendauer T:
1  ​ .
f = ​ __
T
Iterationsbeispiel: ↑12 ↑13 Die Graphen der Bewegungsfunktionen verlaufen anfangs nahezu sinus- bzw. kosinusförmig. ↑14 Für größere Zei­
ten nimmt die berechnete Amplitude zu – im Gegensatz zur Realität.
√ 
√ 
√ 
– k · x0
a0 = ​ ______
 
m ​ 
v1 = v0 + a0 · ∆t
1 ​  · (v + v ) · ∆t
x1 = x0 + ​ __
0
1
2
t1 = t0 + ∆t
F
0
12 Federpendel
9783464853184 Inhalt_S229 229
x
in
sta
0 · ∆t
nd
0
out
Zu
in
sta
nd
1 · ∆t
in
sta
2 · ∆t
nd
Ausgabe
Eingabe
1
out
Zu
Eingabe
Ausgabe
Eingabe
2
out
Ausgabe
7 Prinzip der Iteration
x
in m
freier Fall
40
Zu
– k · x1
 
a1 = ​ ______
m ​ 
…
13 Rechenschritt (Federpendel)
600
500
400
300
200
100
0
freier Fall
mit Luftwiderstand
0
5
10
t in s
10 t-x-Diagramm (∆t = 1 s)
(  )
(  )
x(t) = xmax · cos ​ 2π · ​ __t  ​   ​
T
v(t) = – vmax · sin ​ 2π · ​ __t  ​   ​
T
__
k
__
mit vmax = ​ ​    ​ ​   · xmax
m
a(t) = – amax · cos ​ 2π · ​ __t  ​   ​
T
k
__
mit amax = ​    ​  · xmax
m
( 
√ 
)
11 Bewegungsfunktionen einer harmonischen Schwingung (Start mit maximaler Auslenkung aus der Ruhe heraus)
4
2
0
–2
x a
v
1
2
3
t in s
–4
14 Iterativ berechnete Graphen
25.08.2008 12:18:25 Uhr
230
Grundwissen Physik
von oben
von vorn
x
y
von der
Seite
y(x) = –
g
· x2
2 · v02
Ausblick: Waagerechter Wurf Der waagerechte Wurf lässt sich mithilfe
zweier zueinander senkrechter Teilbewegungen beschreiben. ↑1 Ohne Luftwiderstand gilt:
– Von vorn beobachtet man einen freien Fall in negativer y-Richtung.
– Von oben beobachtet man eine Bewegung in x-Richtung mit konstanter
Geschwindigkeit.
g
Die Bahnkurve ist Teil einer Parabel: y(x) = – ______2 · x 2.
2 · v0
Sie ist umso weiter geöffnet, je größer die Geschwindigkeit v0 ist. Den Betrag
der Bahngeschwindigkeit v erhält man aus den Teilgeschwindigkeiten:
__________
v = √v02 + (g · t)2 .
x(t) = R · cos(w t)
1
y
a=wt
R
x
y(t) = R · sin(w t)
2
v
FZ
2
FZ = m ∙ v = m ∙ w2 ∙ R
R
v = 2πR = w R
T
3
Gleichförmige Kreisbewegung Die Periodendauer T ist indirekt proportional zur Winkelgeschwindigkeit w (im Bogenmaß):
2 π (Einheit der Winkelgeschwindigkeit: _1).
w = ___
s
T
Die Winkelgeschwindigkeit w ist proportional zur Frequenz f der Kreisbewegung: w = 2 π f.
Für die Bahngeschwindigkeit v des Körpers auf der Kreisbahn gilt:
2 π R = w R (R: Radius der Kreisbahn).
v = _____
T
Befindet sich der Körper zur Zeit t = 0 s am Punkt (R|0), dann lassen sich die
t-x- und t-y-Funktionen als Sinus- und Kosinusfunktionen angeben: ↑2
x(t) = R · cos(w t) und y(t) = R · sin(w t).
Es wirkt ständig eine zum Mittelpunkt der Kreisbahn gerichtete Zentripetalkraft FZ auf den Körper. ↑3 Es gilt:
2
Zentripetalkraft: FZ = m · v__ bzw. FZ = m · w 2 · R.
R
FZ = __
v 2 bzw. a = w 2 · R.
Zentripetalbeschleunigung: aZ = ___
Z
m R
Der Impuls Je größer die Masse m und die Geschwindigkeit v eines Körpers ist, desto größer ist sein Impuls p:
p = m · v. ↑4
Der Impuls ist wie die Geschwindigkeit eine gerichtete Größe, seine Richtung stimmt mit der Bewegungsrichtung überein.
Impulserhaltungssatz: In einem abgeschlossenen System bleibt der Gesamtimpuls zeitlich konstant. ↑5
Der Gesamtimpuls bleibt erhalten, auch wenn die kinetische Energie abnimmt.
Je größer die Impulsänderung in einer bestimmten Zeitspanne ist, desto
größer ist die Kraft, die sie hervorruft:
∆p
F = ___ . ↑6
∆t
∆p
F = ___
∆t
p=m·v
pges
vor dem Stoß
4 Impuls (Beispiel)
9783464853184 Inhalt_S230 230
5 Impulserhaltung
pges
nach dem Stoß
6 Kraft und Impulsänderung
25.08.2008 12:18:29 Uhr
231
Jahrgangsstufe 10
Wellen Bei mechanischen Wellen breiten sich Schwingungen in Materie aus.
Sie können Energie übertragen, ohne dass Materie transportiert wird.
Bei transversalen Wellen ist die Ausbreitungsrichtung senkrecht zur
Schwingungsrichtung der einzelnen Teilchen (Beispiel: Seilwellen). Bei
longitudinalen Wellen sind Ausbreitungs- und Schwingungsrichtung parallel zueinander (Beispiel: Schallwellen).
– Die Amplitude einer sinusförmigen Welle ist ihre größte Auslenkung. ↑7
– Die Wellenlänge l ist z. B. der Abstand zweier benachbarter Wellenberge.
– Die Frequenz f ist gleich der Frequenz der Teilchenschwingungen.
– Die Ausbreitungsgeschwindigkeit c der Welle beträgt: c = l · f.
Wenn mechanische Wellen durch eine genügend kleine Öffnung dringen,
werden sie merklich gebeugt. ↑8
Interferenz ist die Überlagerung periodischer Wellen mit gleicher Frequenz. Dabei treten Bereiche auf, in denen sich die Wellen verstärken bzw.
abschwächen. ↑9–↑11
y
y
Amplitude
0
x
7
8 Beugung
Blick durch die gedachte Ebene
y
t1
t
Summe
Wellenlänge l
ymax
t
Summe
t2
Bereiche, in denen sich das Wasser
heftig auf und ab bewegt
9 Verstärkung durch Interferenz
10 Auslöschung durch Interferenz
Quantenphysik Licht verhält sich bei der Interferenz am Doppelspalt wie
eine Welle. ↑12 Für die Ausbreitung von Lichtwellen gilt:
m
c = l · f mit c = 2,997 925 · 108 __
s.
Beim punktförmigen Belichten eines Films verhält sich Licht dagegen wie
ein Strom aus einzelnen Teilchen. ↑13
Photonen sind weder Welle noch Teilchen, sondern Quantenobjekte. Wellenvorstellung (→ Frequenz) und Teilchenvorstellung (→ Energie) sind durch
eine Gleichung verbunden:
EPh = h · f mit h = 6,626 · 10–34 Js (plancksche Konstante).
Beim Fotoeffekt überträgt jeweils ein Photon diese Energie vollständig auf
ein Elektron in einer Metalloberfläche und setzt es damit frei.
Auch bei Elektronen kann man Interferenz- und Beugungserscheinungen an
geeigneten Spalten beobachten.↑14 Elektronen sind ebenfalls Quantenobjekte. Wellenvorstellung (→ Wellenlänge) und Teilchenvorstellung (→ Masse,
h
Geschwindigkeit) sind hier durch folgende Gleichung verbunden: l = _____
m ·v.
11 Blick durch eine gedachte Ebene,
die parallel zur Doppelspaltebene ist
12 Interferenzbild von Licht
hinter einem Doppelspalt
13 Punktförmige Belichtung durch
Photonen
0,001 mm
e
Jedem Quantenobjekt wird eine mathematische Wahrscheinlichkeitswelle zu- 14 Interferenzbild von Elektronen
geordnet. Sie berücksichtigt alle möglichen Zustände des Quantenobjekts und hinter einem Doppelspalt
erlaubt es, die Wahrscheinlichkeit für ein bestimmtes Verhalten zu berechnen.
Durch Messung präpariert man aus den möglichen Zuständen einen heraus.
1s-Orbital
z
In den Atomhüllen lassen sich keine Elektronenbahnen angeben, sondern Orbitale, in denen sich die Elektronen mit großer Wahrscheinlichkeit aufhalten. ↑15 Die Energie der Elektronen ist von Orbital zu Orbital verschieden.
Wechselt ein Elektron das Orbital, ist damit die Aufnahme oder Abgabe einer
x
y
ganz bestimmten Energieportion verbunden.
15 1 s-Orbital des Wasserstoffatoms
2p-Orbitale
9783464853184 Inhalt_S231 231
x
z
y
25.08.2008 12:18:32 Uhr