W - Drucken
Werbung

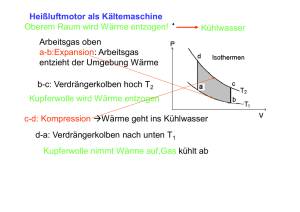
13. Entropie und Zweiter Hauptsatz 13.1 Entropie Wir haben festgestellt, dass der reversible isochore und der reversible isotherme Prozess durch die Konstanz einer Zustandsgröße charakterisiert war (V bzw. T, U). Der adiabatische Prozess hingegen wurde dadurch definiert, dass er ohne Austausch von Wärme abläuft, also dQ = 0, wobei Q keine Zustandsgröße ist. Allerdings ist auch der adiabatische Prozess durch die Konstanz einer Zustandsgröße charakterisiert, nämlich der Entropie S, die folgendermaßen definiert ist: dQrev dS = T 2 bzw. dQrev T 1 ΔS = S2 − S1 = ∫ Beim reversiblen adiabatischen Prozess bleibt also die Entropie S konstant (dQrev=0 Æ ΔS = 0). Die Einheit der Entropie ist Joule/Kelvin. Die Entropie ist eine Zustandsgröße, ihre Änderung ist also nur durch Anfangs- und Endzustand gegeben, unabhängig davon, ob das System einen reversiblen oder einen irreversiblen Prozess durchlaufen hat. Dies erlaubt die Berechnung der Entropieänderung auch im Falle einer irreversiblen Prozessführung. Man wählt sich hierfür einen reversiblen Ersatzprozess, der vom selben Anfangszustand zum selben Endzustand führt und berechnet die Entropieänderung anhand der Definitionsgleichung. Obwohl die ausgetauschte Wärmemenge dQrev im reversiblen Ersatzprozess nicht derjenigen im irreversiblen entspricht, erhält man für die Entropieänderung ein korrektes Ergebnis, eben weil die Entropie eine Zustandsgröße ist. Für die ausgetauschte Wärmemenge gilt im irreversiblen Fall: dQirrev < dQrev = TdS Unter Berücksichtigung des Vorzeichens (aufgenommene Wärme wird positiv, abgegebene negativ gezählt) gilt, dass bei irreversibler Entropiezunahme weniger Wärme aufgenommen wird als bei reversibler Prozessführung, während bei irreversibler Entropieabnahme mehr Wärme abgegeben wird als im reversiblen Fall. Wir betrachten die Entropieänderung bei der Expansion eines Gases, und zwar zunächst im reversiblen isothermen Fall: V1, P1, T V2, P2, T Aus dem ersten Hauptsatz und ΔU = 0 (isotherm) folgt: dU = 0 = dQrev − PdV = TdS − PdV ⇒ dS = P dV dV = nR T V ⇒ ΔS = S2 − S1 = nR ⋅ ln V2 V1 Die aufgenommene Wärme dQrev wurde einem Reservoir gleicher Temperatur (reversibel!) entnommen, dessen Entropie um den Entsprechenden Betrag ΔS abgenommen hat. Die Gesamt-Entropie von Gas und Reservoir (Universum) bleibt im reversiblen Fall also konstant. Für den vollständig irreversiblen Fall stellen wir uns vor, dass die Trennwand plötzlich entfernt wird und das Gas frei in das vorher evakuierte Teilvolumen einströmen kann. Das Gas ist thermisch isoliert, so dass keine Wärme mit der Umgebung ausgetauscht werden kann (dQirrev=0). V1, P1, T V2, P2, T Hier wird keine Arbeit verrichtet, da das Gas frei ins Vakuum strömt (keine Gegenkraft). Außerdem soll keine Wärme ausgetauscht werden, so dass nach dem ersten Hauptsatz die innere Energie und damit die Temperatur konstant bleiben. Da die Entropie eine Zustandsgröße ist, hat sie sich um den gleichen Betrag vergrößert wie im reversiblen Fall. Da sich das Gas jedoch in thermischer Isolation befindet, bedeutet dies, dass die Gesamt-Entropie (Gas plus Umgebung) zugenommen haben muss. 13.2 Zweiter Hauptsatz der Wärmelehre Diese Beobachtung hat allgemeine Gültigkeit und ist Aussage des zweiten Hauptsatzes der Wärmelehre: Die Entropie ist eine Zustandsgröße und besitzt daher in jedem Gleichgewichtszustand einen eindeutigen Wert, unabhängig davon, auf welchem Weg das System in diesen Zustand überführt wurde. In einem abgeschlossenen System ist die Änderung der Gesamt-Entropie bei reversiblen Prozessen gleich null, bei irreversiblen Prozessen größer null. Warum ist die eben diskutierte freie Expansion irreversibel? Warum sammeln sich nicht alle Gasteilchen spontan wieder im kleineren Teilvolumen V1? In der Tat wäre dies nicht im Widerspruch zum ersten Hauptsatz, also verträglich mit der Energieerhaltung. Betrachten wir ein einzelnes Teilchen: Die Wahrscheinlichkeit, es zu einem bestimmten Zeitpunkt innerhalb des Teilvolumens V1 anzutreffen, ist p1 = V1 / V2. Für zwei Teilchen ist die Wahrscheinlichkeit p2 = (V1 /V2)2, beide gleichzeitig innerhalb von V1 anzutreffen. Für N = n NA Teilchen gilt schließlich: ⎛V pN = ⎜⎜ 1 ⎝ V2 ⎞ ⎟⎟ ⎠ N Diese Zahl ist für makroskopische Stoffmengen unvorstellbar klein. Eine solche spontane Ansammlung der Gasteilchen im kleineren Teilvolumen V1 wäre mit einer negativen Entropieänderung verbunden: ΔS = nR ln V1 <0 V2 ⎛V V = Nk B ln 1 = k B ln⎜⎜ 1 V2 ⎝ V2 N ⎞ ⎟⎟ = k B ln pN ⎠ Die Entropieänderung ist also offenbar verknüpft mit der Wahrscheinlichkeit, dass das System in dem einen oder anderen Zustand vorliegt. Die Erkenntnisse des zweiten Hauptsatzes lassen sich also auch so formulieren: eine Abnahme der Entropie im Gesamtsystem wäre gleichbedeutend damit, dass das System von einem sehr wahrscheinlichen in einen sehr unwahrscheinlichen Zustand übergeht. Daher wird die Entropie des Gesamtsystems immer ansteigen oder – im reversiblen Fall – bestenfalls gleich bleiben. Der Gleichgewichtszustand ist stets der Zustand maximaler Entropie, den das System einnehmen kann. Man spricht auch vom Zustand maximaler Unordnung. 13.3 Wärmekraftmaschinen In der Technik sind Maschinen, die Wärme in mechanische Arbeit umwandeln, von großer Bedeutung. Als Beispiel für eine solche Wärmekraftmaschine betrachten wir den Verbrennungsmotor: Im Verdichtungstakt wird das kalte Luft-Benzin-Gemisch adiabatisch komprimiert. Dadurch erhöhen sich P und T. Anschließend wird das Gemisch gezündet, wodurch sich bei praktisch gleich bleibendem Volumen der Druck und Temperatur weiter erhöhen. Der hohe Druck bewegt den Kolben, wodurch das Gemisch adiabatisch expandiert und mechanische Arbeit leistet. Schließlich wird das verbrannte Gemisch ausgelassen und durch neues, kaltes Gemisch ersetzt. Der Zyklus beginnt von neuem. Für unsere Diskussion sind wir nicht an den Details der technischen Realisierung interessiert, sondern an den thermodynamischen Prinzipien. Entscheidend ist, dass der Maschine eine Arbeitssubstanz zugrunde liegt (Verbrennungsmotor: Benzin-Luftgemisch, Dampfmaschine: Wasserdampf), die Wärme und mechanische Arbeit aufnehmen und abgeben kann. Wichtig ist außerdem, dass Wärmekraftmaschinen zyklisch arbeiten, also Anfangs- und Endzustand eines Prozesses gleich sind und sich wiederholen. Der Zyklus eines Verbrennungsmotors sieht vereinfacht etwa so aus: (a-b): adiabatische Kompression. Die Arbeit W1 wird der Substanz zugeführt (b-c): isochore Erwärmung. Die Wärme Qw wird zugeführt (c-d): adiabatische Expansion. Die Arbeit W2 wird verrichtet P c b d (d-a): isochore Abkühlung. Die Wärme Qk wird abgegeben a V Kehrt das System nach einem vollen Umlauf an seinen Ausgangspunkt zurück, ist die Änderung der inneren Energie null. Nach dem ersten Hauptsatz gilt dann ΔU = W1 + Qw − W2 − Qk = 0 a →a Die netto verrichtete Arbeit ist W = W2 – W1, also gleich der von den Kurven eingeschlossenen Fläche. Daraus folgt W = Qw − Qk Man definiert den Wirkungsgrad ε einer Wärmekraftmaschine als das Verhältnis aus der netto verrichteten Arbeit und der aufgenommen P Wärme: c W Qw − Qk Qk ε= = =1 − Qw Qw Qw Es wird also stets nur ein Teil der aufgenommenen Wärme in Arbeit Umgesetzt. Der Rest wird in Form der Wärme Qk an die Umwelt abgegeben. b d a V Beispiel: Eine Wärmekraftmaschine nimmt eine Wärmemenge von 200 J aus einem heißen Reservoir auf, verrichtet die Arbeit W und gibt 160 J an ein kaltes Reservoir ab. Wie hoch ist der Wirkungsgrad ε? 13.4 Der Carnot-Prozess Der französische Ingenieur Carnot hat im Jahr 1824 gezeigt, dass zwischen zwei gegebenen Wärmereservoirs die reversibel arbeitende Wärmekraftmaschine den größtmöglichen Wirkungsgrad besitzt. Wir betrachten den Carnot-Kreisprozess: (a-b): isotherme Expansion (T = Tw) (b-c): adiabatische Expansion (c-d): isotherme Kompression (T = Tk) (d-a): adiabatische Kompression P T Tw a b Tk Tw d c a b d c Tk V S1 S2 S Bei reversibler Prozessführung sind die Verhältnisse im TS-Diagramm besonders übersichtlich. Die aufgenommene Wärme in jedem Umlauf entspricht gerade der rot eingerahmten Fläche: Qrev = Qw − Qk = (Tw − Tk )(S2 − S1 ) Nach dem ersten Hauptsatz îst dies gleich der verrichteten Arbeit W, also der rot eingerahmten Fläche im PV-Diagramm. P T Tw a b Tk Tw d c a b d c Tk V S1 S2 S Für den Wirkungsgrad gilt ε= W Qw − Qk Q = =1 − k Qw Qw Qw Bei reversibler Prozessführung ist dQrev = TdS, also ε rev = 1 − Qk T (S − S1 ) T =1 − k 2 =1 − k Qw Tw (S2 − S1 ) Tw Selbst bei reversibler Prozessführung kann der Wirkungsgrad einer Wärmekraftmaschine also nur theoretisch eins werden, wenn nämlich die Temperatur des kälteren Wärmebades gleich dem absoluten Nullpunkt ist. Bei irreversibler Prozessführung ist wegen dQirrev < dQrev die aufgenommene Wärmemenge Qw kleiner und die abgegebene Wärmemenge Qk größer (Vorzeichen!) als im reversiblen Fall. Dann gilt also: ε irrev < ε rev = 1 − Tk Tw Wir fassen dies nochmals zusammen: • Eine zyklisch arbeitende Wärmekraftmaschine kann selbst bei reversibler Prozessführung niemals die gesamte aufgenommene Wärmemenge in mechanische Arbeit umwandeln. Ein Teil der aufgenommene Wärme muss an ein kälteres Wärmebad abgeführt werden. • Bei gegebenem Tw und Tk wird der maximale Wirkungsgrad bei reversibler Prozessführung erreicht (Carnot-Prozess). irreversibel reversibel Tw Tw Qw Qw W W Qk Qk Tk Tk 13.5 Kältemaschinen und Wärmepumpen Kältemaschinen und Wärmepumpen basieren auf dem Prinzip, dass in einem Kreisprozess Wärme aus dem kälteren Reservoir entnommen wird (dieses sich also weiter abkühlt) und dafür Wärme an das wärmere Reservoir abgegeben wird (dieses sich also weiter aufwärmt). Das kann erreicht werden, indem der Arbeitszyklus einer Wärmekraftmaschine umgedreht wird, wobei dann natürlich netto mechanische Arbeit dem System zugeführt werden muss. Für den reversiblen Fall: reversibel P T Tw b b Tw a Qw W a Tw c d Tk c Qk d Tk Tk V S1 Man definiert die Leistungszahl cL für Kältemaschinen und Wärmepumpen: S2 S cL = Qk W