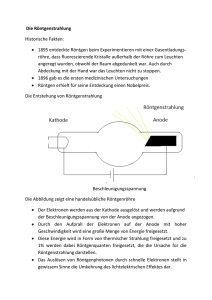
Versuch 502 - Röntgenstrahlung - alexander

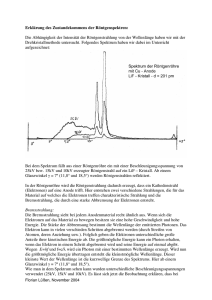
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
o Aufgaben:
1. Messen Sie nach Einsetzen eines Plattenkondensators in die im Innenraum des Röntgengerätes dafür
vorgesehenen Steckverbindungen und den Anschluss der externen Spannungsversorge- und
Verstärkereinheit die Luftionisation zwischen den Platten eines Flächenkondensators aus Aluminium als
Funktion der Röntgenstrahlintensität. Stellen Sie ihre mehrfach aufgenommenen Messwerte in einem
geeigneten Diagramm grafisch dar und interpretieren Sie ihre Ergebnisse.
2. Bestimmen Sie nach Einbau des Spaltkollimators mit Zr-Filter und der Diffraktometereinheit unter
Verwendung des Al-Absorbersatzes mit Aluminium-Blechen unterschiedlicher Dicke (D = 0, 0.5, 1.0,
1.5, 2.0, 2.5, 3.0 mm) den Massenschwächungskoeffizienten µ/p für Aluminium unter Anwendung des
Schwächungsgesetzes. Präsentieren Sie Ihre Ergebnisse in einem geeigneten Diagrammformat.
3. Nehmen Sie die spektrale Intensitätsverteilung der Molybdän-Röntgenröhre durch Zerlegung der
Röntgenstrahlung über einen Kristallmonochromator auf. Befolgen Sie vor Starten des Scan-Modus die
in der Praktikumsanleitung und die in der am Versuchsplatz ausliegenden Gerätebeschreibung
ausgewiesenen Schritte zur Eingabe der Parameter. Nach Aufnahme der Datensätze und grafischer
Wiedergabe berechnen Sie die Wellenlängen λ in nm der MoKα- und MoKβ-Peaks verschiedener
Ordnungen und die Wellenlänge λG der kurzwelligen Kante des Spektrums mithilfe der BraggGleichung.
o Grundlagen und Vorbetrachtungen:
Der Höhepunkt der Theorie des Elektromagnetismus im 19. Jahrhundert war die vom schottischen
Physiker James Clerk Maxwell beschriebene Vorhersage, dass sich elektrische und magnetische Felder in
Form von Wellen im Raum ausbreiten. Ein zeitlich verändertes Magnetfeld erzeugt dabei ein elektrisches
Feld und umgekehrt ein sich änderndes elektrisches Feld ein Magnetfeld. Folge dieser Wechselwirkung
sind Wellen, die sich im Vakuum mit Lichtgeschwindigkeit ausbreiten können. Im Strahlungsfeld stehen
elektrische und magnetische Feldstärke E und B in jedem Punkt senkrecht zueinander und bilden eine
Transversalwelle.
Die in der elektromagnetischen Welle gespeicherte Energie ist proportional zum Quadrat der Amplitude
von E und B. Beschleunigte elektrische Ladungen erzeugen elektromagnetische Wellen. Experimentell
nachgewiesen wurden elektromagnetische Wellen 1887 von Heinrich Hertz, acht Jahre nach Maxwells
8
Tod. Da sie neben einer berechneten Ausbreitungsgeschwindigkeit von 3 · 10 m/s im luftleeren Raum
auch für Licht typische Eigenschaften, wie Reflexion, Brechung und Interferenz aufwiesen, wurde die
Zuordnung des sichtbaren Lichtes zum elektromagnetischen Spektrum von der Wissenschaft anerkannt.
Im Jahre 1895 entdeckte Wilhelm Conrad Röntgen, dass fluoreszierende Minerale zu leuchten beginnen
und ein fotographischer Film belichtet wird, wenn in einer etwas entfernten Vakuumröhre Elektronen durch
eine hohe Spannung beschleunigt werden und auf eine Glas- oder Metalloberfläche innerhalb der Röhre
treffen. Er nannte die unbekannten Strahlen „X-Rays“. Die nach ihm benannte Röntgenstrahlung ist eine
elektromagnetische Welle kurzer Wellenlänge und entsteht beim Zusammenstoß von energiereichen
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
1
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Elektronen mit Atomen hoher Ordnungszahl oder bei Geschwindigkeitsänderung stark beschleunigter
geladener Teilchen. Die Erforschung der Röntgenstrahlung zeigte, dass es sich nicht um geladene
Teilchen handelte, da sie nicht mittels elektrischer oder magnetischer Felder abgelenkt werden konnten.
Zur Erzeugung von Röntgenstrahlung verwendet man
Hochvakuum-Röntgenröhren. Nach Anlegen einer
Hochspannung von 10 bis 100 kV werden Elektronen
aus einer Glühkathode emittiert und zur gegenüberliegenden Anode beschleunigt. Beim Auftreffen auf das
hitzebeständige und gut wärmeleitende Anodenmaterial
wird ein Teil der kinetischen Elektronenenergie in
elektromagnetische Strahlung kurzer Wellenlänge
umgesetzt, wobei der verbleibende Energierest als
Wärme an die zu kühlende Anode angeben wird. Als
Anodenmaterial verwendet man meist Molybdän, wie
unserem Versuch, oder Wolfram. Mit Erhöhung der
Beschleunigungsspannung und der damit verbundenen
erhöhten kinetischen Energie der auf die Anode
auftreffenden Elektronen wächst die Durchdringungsfähigkeit der Strahlung und damit die Härte. Die
Intensität wird von der Anzahl der aus der Kathode austretenden Elektronen bestimmt und ist von der
Glühtemperatur der Kathode abhängig.
Die Linienspektren der Atome im sichtbaren, UV- und Infrarot-Bereich des elektromagnetischen Spektrums
gehen auf die Übergänge der Valenzelektronen zwischen unterschiedlichen Zuständen zurück. Die
Kernladung wird gegenüber den Außenelektronen durch die inneren Elektronen größtenteils abgeschirmt.
Die inneren Elektronen der Schale m=1 bekommen dabei die gesamte Kernladung zu spüren. Da die
Energie eines Niveaus proportional zur Ordnungszahl ins Quadrat ist, erwartet man beispielsweise bei einem
-2
-1
Atom mit OZ=50, 2500-mal kürzere Wellenlängen (10 bis 10 nm) – Wellenlängen im Röntgenbereich des
elektromagnetischen Spektrums. Das von den Röntgenquanten erzeugte Röntgenspektrum unterscheidet
man je nach Erzeugungsprozess in ein kontinuierliches Spektrum mit der Grenzwellenlänge λG und eine
Folge von Peaks, die als charakteristische Strahlung dem kontinuierlichen Spektrum überlagert ist. Das
Bremsspektrum und die Grenzwellenlänge sind spannungsabhängig und bewegen sich nach links, wenn die
Spannung in der Röntgenröhre erhöht wird. Die mit MoKα und MoKβ betitelten Peaks bleiben ihren
Wellenlängen bei Spannungsveränderungen treu und verändern ihre Position bei unterschiedlich
verwendeten Targetmaterialien.
Wilhelm Conrad Röntgen (1845-1923)
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
2
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Beim Eindringen in das Anodenmaterial werden die hochbeschleunigten Elektronen aufgrund der
Coulomb-Wechselwirkungen mit den positiv geladenen Atomkernen sowie ihre Hüllenelektronen
kontinuierlich abgebremst – Entstehung von Bremsstrahlung. Die Elektronen geben dabei ein Großteil ihrer
Energie als Wärme ab, oder sie emittieren Röntgenphotonen. Aufgrund der Energieerhaltung muss die
Energie des emittieren Photons EPhoton= hf gleich dem Verlust an kinetischer Energie ∆Ekin sein. Ein
Elektron kann beim Zusammenstoß mit dem Targetmaterial seine gesamte Energie oder nur einen Teil
davon verlieren, sodass es sich beim kontinuierlichen Spektrum um eine Pulsfolge unterschiedlicher
Photonenenergien handelt. Die kürzeste Wellenlänge bzw. die höchste Frequenz f muss somit von einem
Elektron stammen, das seine gesamte kinetische Energie abgibt und beim Stoß ein einzelnes Photon
erzeugt. Da die kinetische Ausgangsenergie gleich der Energie sein muss, die das Elektron durch die
Beschleunigung im elektrischen Feld erfährt, muss Ekin = eU sein. Im Falle eines einzelnen Stoßes, bei
dem das Elektron zur Ruhe kommt gilt folgende Gleichung:
EPhoton = h·f = hc/λG = eU = Ekin
wobei λG = c/f gleich der Grenzwellenlänge der typischen kurzwelligen Kante des Bremsspektrums ist.
Beim Zusammenstoß der Elektronen mit den Atomen des
Anodenmaterials können diese angeregt und ionisiert
werden, wodurch gebundene Elektronen des Anodenatoms auf ein höheres unbesetztes Energieniveau
gehoben oder ganz aus dem Atomverbund herausgeschlagen werden. Bei ausreichend hoher kinetischer
Energie der Kathodenelektronen werden auch innere,
kernnahe Atomelektronen der K-Schale herausgeschlagen
und in ein äußeres Energieniveau gehoben oder ins
Kontinuum freigesetzt. Das so entstandene unbesetzte
Energieniveau wird durch Elektronensprünge aus benachbarten höheren Energieniveaus wieder aufgefüllt. Die
dabei freiwerdende Energie wird als Strahlungsquant
freigesetzt, das für das Atom des Anodenmaterials mit
einer charakteristischen Wellenlänge verknüpft ist,
wodurch die Peaks des charakteristischen Röntgenspektrums zustande kommen. Elektronensprünge auf die
K-Schale ergeben die charakteristische K-Strahlung. Von
Kα-Strahlung spricht man, wenn die Elektronensprünge
von der L-Schale ausgehen, von Kβ-Strahlung, wenn die
M-Schale als Herkunftsort definiert wird.
Nach Entdeckung der Röntgenstrahlen kursierte die Annahme, Röntgenstrahlen seien eine Form
unsichtbaren Lichtes. Jedoch zeigten sie keinerlei Beugungs- oder Interferenzerscheinungen, wenn man
gewöhnliche Beugungsgitter benutzte. Wenn allerdings ihre Wellen-6
längen viel kleiner sind als der typische Gitterabstand von 10 m,
kann man keine Effekte erwarten. Deshalb schlug 1912 Max von
Laue vor, dass man einen Kristall mit periodisch angeordneten
Atomen als Beugungsgitter verwenden könnte. Und tatsächlich
konnte experimentell gezeigt werden, dass die am Kristall gestreuten
Röntgenstrahlen die typischen Berge und Täler des Beugungsmusters aufwiesen. Erkenntnis dieser Versuchsreihen: Röntgenstrahlen besitzen Welleneigenschaften und die Atome in Kristallen
sind periodisch angeordnet. In einem einfachen Kristall, wie NaCl
sind die Atome in einem kubischen Gitter zusammengefasst, wobei
die Atome jeweils den Abstand d voneinander haben. Fallen
Röntgenstrahlen und einem Winkel auf die Kristalloberfläche, dann
werden die auf zwei unterschiedlichen Ebenen reflektierten Strahlen
konstruktiv miteinander interferieren.
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
3
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Unter Ausnutzung dieser Interferenz lässt sich
polychromatische Röntgenstrahlung monochromatisieren,
wobei die Bragg-Gleichung gilt:
mλ = 2d · sin Φ
wobei m die intensitätsstarken Interferenzmaxima der
Ordnungen m = 1, 2, 3 beschreibt.
Fällt eine ebene Röntgen-Lichtwelle auf eine lineare
Reihe von Atomen mit dem Abstand d, so werden diese
als Zentren Huygen’scher Elementarwellen zur Emission
von Sekundarwellen angeregt, die miteinander
interferieren. Handelt es sich um eine polykristalline
Substanz erhält man anstelle der Laue-Flecken
konzentrische Kreise.
Röntgenstrahlung wird beim Durchgang durch Materie geschwächt. Die Schwächung ist allerdings
abhängig von der Wellenlänge der verwendeten Röntgenstrahlung, andererseits von den Eigenschaften
des schwächenden Materials (z.B. Dichte oder Ordnungszahl). Es gilt das so genannte
Schwächungsgesetz:
-µD
I = I0 e
Der lineare Schwächungskoeffizient µ setzt sich aus dem photoelektrischen Absorptionskoeffizienten τ und
dem Koeffizienten unterschiedlicher Streumechanismen σ additiv zusammen, wobei gilt: σ << τ. Als
unabhängige Größe vom Zustand des Absorbers gilt der Massenschwächungskoeffizient k = µ/ρ. Generell
schwächen die Elemente hoher Ordnungszahl Röntgenstrahlen besonders stark. Trägt man den
Massenschwächungskoeffizienten k gegen die Wellenlänge im Diagramm auf, erkennt man typische
Absorptionskanten.
Die ionisierende Wirkung von Röntgenstrahlung wird zum qualitativen Nachweis und zur quantitativen
Registrierung genutzt. Neben Fluoreszenzerscheinungen am Leuchtschirm gibt es Detektoren zur
elektronischen Registrierung, wovon das Geiger-Müller-Zählrohr die Liste anführt.
Das Zählrohr besteht aus einem halboffenen Metallzylinder, der als Kathode geschaltet ist und in dem sich
axial ein dünner Metalldraht als Anode befindet. Eine dünne, für Röntgenstrahlung durchlässige Folie trennt
als Eintrittsfenster die Außenluft von einem Edelgas-Halogen-Gemisch unter vermindertem Druck. Zwischen
Anode und Kathode liegt eine Spannung
von 300 bis 2000 V an. Die einfallenden
Röntgenquanten ionisieren die
Gasatome, wobei die Elektronen zur
Anode beschleunigen und ihrerseits
weitere Atome ionisieren, wodurch eine
Ladungslawine entsteht, die einen
registrierbaren Stromimpuls erzeugt.
Durch die trägeren positiven Ionen bildet
sich um den Anodendraht ein positiver
Raumladungsschlauch, der eine weitere
Entladung verhindert und keine
Lawinenbildung zulässt. Man spricht von
einer Totzeit, die nach Abwanderung der
positiven Ionen zur Kathode und
dortigen Neutralisation endet und damit
das Zählrohr wieder empfangsbereit ist.
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
4
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
o Versuchsdurchführung:
Grundlage für die Versuchsdurchführung war das Röntgengerät der Firma Leybold-Didactic, über dessen
Aufbau das folgende Bild Auskunft geben soll:
a)
Messung der Luftionisation – Versuch 1
Nach Vertrautmachen mit den Bedienelementen und der ausliegenden Gerätebeschreibung begann der
Ausbau der Diffraktometereinheit mit dem Targettisch und dem Geiger-Müller-Zählrohr. Außerdem wurde
der Spaltkollimator entfernt, um die gesamte Röntgenstrahldosis während des Versuchs 1 in den
Experimentierraum zu lassen. Nach Einbau des Plattenkondensators in die vorgesehenen Steckverbinder
und Verbindung der oberen Kondensatorplatte mit dem positiven Pol der externen Spannungsversorgungseinheit und dem Verbinden der unteren Kondensatorplatte mit der Verstärkeeinheit, begann nach
Schließung des Experimentierraumes das Einschalten des Röntgengerätes und das Anlegen der
Hochspannung von 35 kV mit Hilfe des Adjust-Rades. Im Anschluss wurde der Röntgenemissionsstrom Iem
in mA in 0,1-Schritten von 0 bis 1 mA hochgeregelt und der Ionisationsstrom Iio am externen Voltmeter
abgelesen. Nach dreimaliger Durchführung der Versuchseinheit wurden folgende Messwerte ermittelt:
Iem in mA
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
Messung des Ionisationsstroms in nA
Iio Reihe 1
Iio Reihe 2
Iio Reihe 3
0
0
0
0,35
0,36
0,36
0,69
0,70
0,70
1,03
1,04
1,03
1,37
1,37
1,37
1,71
1,70
1,70
2,03
2,03
2,04
2,36
2,37
2,37
2,71
2,71
2,71
3,04
3,03
3,03
3,35
3,36
3,37
Iio Intervall
0,00-0,01
0,35-0,37
0,69-0,71
1,02-1,04
1,35-1,39
1,68-1,73
2,01-2,08
2,34-2,40
2,68-2,74
3,00-3,07
3,33-3,41
-9
Der reale Ionisationsstrom trägt die Einheit 10 nA, kann aber durch die Verstärkereinheit eines STE9
Widerstandes von 1 GΩ = 10 Ω vom Voltmeter ohne Umrechnung abgelesen werden.
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
5
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Die graphische Darstellung äußert sich in folgendem Diagramm:
Auswertung Versuch 1:
Die in der Hochvakuum-Röntgenröhre beschleunigten Kathodenelektronen treffen auf das angewinkelte
Anodenmaterial und senden kurzwellige Röntgenquanten in den Experimentierraum. Die zwischen den
Kondensatorplatten befindliche Luft (Gasatome) wird ionisiert, dass heißt die aus den Gasatomen
herausgeschlagenen Elektronen wandern zur oberen, positiven Kondensatorplatte, die positiven Ionen
wandern zur unteren Kondensatorplatte. Im elektrischen Feld des Plattenkondensators wird ein
Ionisationsstrom registriert. Trägt man die Werte des Röntgenemissionsstroms gegen die Werte des
Ionisationsstroms auf, so erhält man, wie im Diagramm ersichtlich, eine lineare Abhängigkeit. Das Ablesen
des Ionisationsstroms vom Voltmeter gestaltete sich durch schwankende Werte schwierig. Wie man der
Tabelle entnehmen kann, steigt das angezeigte Werteintervall mit zunehmendem Emissionsstrom an.
Grund für die Schwankungen ist die ungleichmäßige Aussendung von Röntgenquanten.
b)
Schwächung der Röntgenstrahlung – Versuch 2
Nach Ausschalten der Hochspannung wurde der Plattenkondensator wieder ausgebaut und die
Diffraktometereinheit eingesetzt und angeschlossen. An den beweglichen Probehalter haben wir den
Aluminium-Absorbersatz eingesetzt, der aus sechs Aluminiumblechen unterschiedlicher Dicke besteht.
Außerdem wurde der mit einem Zirconium-Filter bestückte Spaltkollimator angebracht. Nach Verschluss
des Experimentierraumes wurde eine Hochspannung der Röntgenröhre von 25 kV eingestellt, der
Röntgenemissionsstrom beträgt wie beim ersten Versuch 1 mA. Wichtig ist die ebene Ausrichtung von
Spaltkollimator, Absorber und Geiger-Müller-Detektor. Insgesamt wurden sieben Messungen je dreimal
durchgeführt. Dabei muss der Winkel des Absorbersatzes so optimiert werden, dass jeweils die
durchschnittlich meisten Zähleinheiten des Detektors in counts per second (cps) registriert wurden. Der
erste Wert wurde ohne Abschirmung der Strahlung aufgenommen. Danach wurde er Winkel jeweils um 10°
erhöht, bis die maximale Dicke des Aluminiumbleches von 3 mm bei ungefähr 60° erreicht war. Bei diesem
Versuchsteil wurde das Ablesen der „Counts per second“ aufgrund der großen Schwankungsbreite zur
Herausforderung. Folgende Werte wurden nach bestem Gewissen aufgestellt:
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
6
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Messung der Anzahl der registrierten Stromimpulse in cps je Abschirmungsgrad
DickeAlu in mm Target-Winkel
cps Reihe 1
cps Reihe 2
cps Reihe 3
Mittel cps
0
0,1 °
6410
6390
6360
6390
0,5
10,1 °
4350
4315
4315
4330
1
20,1 °
2470
2460
2450
2460
1,5
30,2 °
1600
1590
1585
1590
2
40,1 °
830
840
835
835
2,5
50,2 °
540
550
545
545
3
60,1 °
330
320
325
325
Trägt man die durchschnittliche Intensität der Röntgenquanten in cps gegen die Dicke der
Aluminiumabschirmung auf, erhält man im folgenden Diagramm einen exponentiellen Kurvenverlauf:
Wie zu erwarten, nimmt die am Intensität der am Zählrohr ankommenden Röntgenstrahlung mit
bx
zunehmender Abschirmung ab und ergibt einen Kurvenverlauf nach dem Typus: y= a·e . Nach Fitten der
Messreihe mit Hilfe des Computerprogramms Origin (rote Kurve) errechnete die Software einen
Abklingkoeffizienten von 0,9476.
Auswertung Versuch 2:
Die Messwerte verdeutlichen dass die Dicke des abschirmenden Materials die Intensität der Röntgenstrahlen bremsen können, wobei die ersten Zehntelmillimeter am wirksamsten sind. Ab 2 mm nimmt der
Rückgang der cps nur noch unbedeutende Ausmaße an. Aluminium selbst ist ein Metall von relativ
geringer Dichte. Dabei nimmt allerdings die Schwächung der im menschlichen Körper Stoffwechselstörungen auslösende Röntgenstrahlung mit zunehmender Ordnungszahl um ein Vielfaches zu. So ist Blei
(OZ 82) ein sehr wirksamer Strahlenabsorber, da hier die dicht gepackten Gitteratome ständig mit den
Röntgenquanten kollidieren. Die Absorption von Röntgenstrahlung einer bestimmten Wellenlänge ist somit
mit der Anregung des absorbierenden Atoms verbunden. So würde man bei einer Untersuchung der
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
7
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Abhängigkeit des Massenschwächungskoeffizienten k von der Wellenlänge Absorptionskanten erhalten.
Bei großen Photonenenergien besteht eine größere Wahrscheinlichkeit, dass selbst die stark gebundenen
Elektronen der K-Schale auf höhere Energieniveaus gehoben werden. Bei steigender Wellenlänge tendiert
die Absorptionswahrscheinlichkeit der K-Schale gegen Null – grafisch als K-Kante ersichtlich. Zwischen
den Absorptionskanten gilt die Proportionalität µ/ρ ~ λ³. Der im Versuch verwendete Zirconium-Filter
begrenzte das Spektrum der Röntgenstrahlen. Ziel dieses Versuches war die Bestimmung des Massenschwächungskoeffizienten für Aluminium auf Grundlage des Schwächungsgesetzes, was die folgende
Rechnung ausführen wird. Bemerkenswert ist dabei die Annäherung des linearen Schwächungskoeffizienten µ an den vom Computerprogramm Origin errechneten Faktor b in der Funktionsgleichung
-µD
y = a·e (Vorzeichenwechsel !)
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
8
Physik
Physikalisches Grundpraktikum
c)
Versuch 502 – Röntgenstrahlung
Spektrale Intensitätsverteilung – Versuch 3
Um das Röntgengerät zur Bestimmung der
wellenlängenabhängigen Intensität im
Spektrometermodus verwenden zu können, haben wir
den Al-Absorbersatz und den Zr-Filter ausgebaut und
den Targettisch mit einem Monochromatorkristall
(NaCl) am Probehalter befestigt. Der Kristall und das
Zählrohr sind zum einfallenden Röntgenstrahl so zu
positionieren, dass jeweils die Winkelpositionen ϑ
bzw. 2ϑ einnehmen. Hierzu sind einige Arbeitsschritte
der Justierung vor Versuchsbeginn notwendig. Nach
Zurückfahren des Target- und Sensorarmes in die
Nullposition, wird der Probehalter um etwa 7,2 °
gedreht. Nach Einschalten der Hochspannung von 35
kV und dem Einstellen des Emissionsstromes von
1 mA wird durch sensibles Einstellen das Maximum der Zählrate für das erste Reflexionsmaximum des Kristalls gesucht. Anschließend haben wir im Couplet-Modus das
Target um genau 7,2 ° zurückgedreht und diese Stell ung als neue Nullposition
gespeichert. Nach Eingabe der Scan-Parameter misst das Röntgengerät alle
2 Sekunden in einer Winkeldifferenz von ∆β = 0,1° die Impulsdichte im Winkelintervall
von 2,5° bis 24°. Ist der automatische Scan abgesch lossen, beginnt das Auslesen
der Werte für die Impulsdichte in cps für alle 216 Winkelwerte, die in ein
Diagramm einfließen.
α1
λG = 3,4 °
β1
α1 = 7,2 °
β1 = 6,4 °
α2 = 14,5 °
β2 = 12,9 °
α3 = 22,1 °
β3 = 19,6 °
α2
β2
β3
α3
λG
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
9
Physik
Physikalisches Grundpraktikum
Versuch 502 – Röntgenstrahlung
Nach Fertigstellung der Wertetabelle wurde ein aussagekräftiger Graph erstellt, bei dem sowohl das
kontinuierliche Spektrum für 1 mA mit der kurzwelligen Kante, als auch das charakteristische
Röntgenspektrum für Molybdän mit seinen Peaks von insgesamt drei Ordnungen (Maxima) sichtbar
werden. Im Folgenden sollen die Berechnungen für die Wellenlängen der α- und β-Peaks sowie λG folgen:
Auswertung Versuch 3:
Die Ergebnisse der Rechnungen zeigen das die α- bzw. β-Peaks des Molybdän jeweils ihre spezifischen
Wellenlängen von 0,071 bzw. 0,063 nm besitzen. Das breite Bremsspektrum erreicht bei ~ 3,4 ° mit 0,033
nm die kleinste Wellenlänge. Bei dieser Frequenz hat ein Kathodenelektron mit Ekin= eU seine ganze
Energie an ein Photon mit EPhoton = hf abgegeben. Die Peaks stellen die Interferenzmaxima der
monochromatisierten Röntgenquanten dar.
13.01.2008
© Januar 2008 by Alexander Jörk und Sarah Hoßfeld
Medizinische Fakultät der Friedrich-Schiller-Universität Jena
10