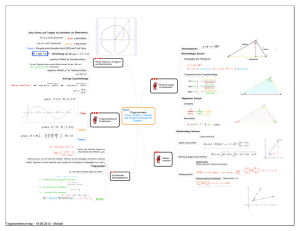
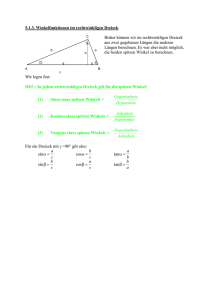
Sinus- Cosinus- Tangens im rechtwinkligen Dreieck
Werbung

In diesem Kurs dreht sich alles um Sinus, Cosinus und Tangens. Bitte nutze diese Übersicht hier über alle Aufgabentypen, damit du dir gezielt die gewünschte Aufgabe bei bettermarks oder bei realmath heraussuchen kannst. Jede Lernplattform hat hier ihre eigenen Vorzüge. Du kannst die Reihenfolge der Übungen selbst bestimmen; bettermarks bietet dir auch Tests an, die du auch zu Beginn zum Testen deines Wissens machen kannst. Beachte: Wenn dein Lehrer einsteigt mit der Definition am Einheitskreis, dann muss du bei bettermarks bei den Übungen (8.1) bis (8.11) einsteigen. Bei realmath steht die Einführung am Einheitskreis sofort unter (1). 1. Sinus- Cosinus- Tangens im rechtwinkligen Dreieck - Einführung Übung (1.1) bis (1.3): Aufstellen der Grundformeln am rechtwinkligen Dreieck. Übung (1.4) bis (1.5): Wie bestimmt man mit dem Taschenrechner den sin/cos/tan-Wert für Winkel zwischen 0° und 90°. Die Erklärung findest du unter „Wissen“ - Buchsymbol anklicken. Übung (1.6) bis (1.9): Hier wird mit sin und cos – nicht mit tan (!)- ein einziges fehlendes Maß im rechtwinkligen Dreieck ausgerechnet. Übungen für Einsteiger mit Anleitung! Übung (1.10) bis (1.15): Fortsetzung von (1.6) bis (1.9):Hier werden jetzt alle fehlenden Maße in einem rechtwinkligen Dreieck mit sin und cos berechnet.Mit Tests (1.13) bis (1.15). 2. Sinus- Cosinus-Tangens im rechtwinkligen Dreieck – Level 2 Übung (2.1) bis (2.4): Hier wurden zwei rechtwinklige Dreiecke zu einer einzigen neuen Figur zusammengesetzt … es sollen die fehlenden Maße mit sin ,cos und tan berechnet werden. Übung (2.5) bis (2.8): Konstruiere hier zu vorgegebenen Sinus- bzw. Cosinuswerten das passende rechtwinklige Dreieck, mit interaktivem Zirkel; in (2.7) sogar mit Tangens. 3. Bunte Mischung aus (1.1) bis (2.8) – Übungen und Tests Übungen (3.1) bis (3.4): Nur bezogen auf das rechtwinklige Dreieck, sonst bunte Mischung, Level 1-2. 4. Textaufgaben aus dem Alltag - mit rechtwinkligen Dreiecken Übung (4.1) bis (4.6): Die Grundfigur ist immer ein rechtwinkliges Dreieck. Mit sin,cos und tan werden hier konkrete Messungen im Alltag durchgeführt. Level 1 – Level 2 und Level 3 Übungen und auch Tests. Du kannst hier die gleichen Aufgaben als Übung (mit Erklärung) oder sofort als Tests (Erklärung am Ende) durchführen. 5. Anwendungen: Vierecke , Vielecke u. Körpern Übung (5.1) bis (5.4): Rechnen mit sin,cos, tan im Rechteck,Trapez und gleichschenkligem Dreieck. Level 1. Übung (5.5) bis (5.6): Rechnen im Parallelogramm. Level 2. Übung (5.7) bis (5.9): Rechnen im gleichseitigen Dreieck, Berechnung der Neigungswinkel im Quader und Pyramide. Level 2-3. Übung (5.10) bis (5.12): Rechnen im Kegel, Pyramide und Quader. Level 3. Übung (5.13) bis (5.14): Rechnen im regelmäßigen Vieleck. Level 3. Übung (5.15): Bunte Mischung zu (5.1) bis (5.14) Test (5.16): Bunte Mischung zu (5.1) bis (5.13) 6. Grundlegende Zusammenhänge zwischen Sinus-Cosinus-Tangens Übung (6.1) bis (6.5): Zusammenhänge zwischen Sinus- und Cosinuswerten und auch Tangens(Level 2). In (6.3) Wiederholung der Def. von sin/cos/tan im rechtwinkligen Dreieck.;Level 1. Übung (6.5): sind/cos/tan von speziellen Winkeln, nämlich 30°, 45° und 60°. Übungen (6.6) bis (6.8): Anwendung der Zusammenhänge aus (6.1) für die Berechnung von fehlenden Werten in einer Wertetabelle; Level 2 – 3. Übung (6.9): Bunte Mischung aus (6.1) bis (6.8). Level 2 bis Level 3. Test (6.10): Bunte Mischung zu (6.1) bis (6.8). Level 2 bis Level 3. 7. Wiederholung von (1) bis (6) – Übungen und Tests - Übung (7.1) – (7.4) Hier hat der Computer nach dem Zufallsprinzip eine Mischung aus allen Aufgabentypen von (1.1) bis (6.8) zusammengestellt. Level 1-3 gemischt. 8. Sinus – Cosinus- Tangens- Einführung am Einheitskreis Beachte: Man kann sin,cos unnd tan auch am Einheitskreis definieren anstatt am rechtwinkligen Dreieck. Das lernst du hier in (8.1) bis (8.11) oder bei realmath unter Punkt (1). Übung (8.1) bis (8.11): Für welche Winkel ist der Sinuswert bzw. der Cosinuswert negativ? Welche Winkel haben den gleichen Sinus- bzw. Cosinuswert ? Sowie einfache Aufgaben der Form: Gesucht ist der Winkel, für den gilt … 9. Sinussatz - Berechnungen in beliebigen Dreiecken Übung (9.1): Herleitung des Sinussatzes. Übung (9.2) bis (Test (9.5): Berechnung einer einzigen fehlenden Größe im beliebigen Dreieck mit Hilfe des Sinussatzes, mit Anleitung. Übung (9.6): Mit gegebenen Maßen nach WSW werden mit dem Sinussatz sämtliche fehlenden Maße selbst berechnet. Die ausführliche Lösung auf Wunsch anzeigen lassen. Level 2-3. Bei realmath findest du dazu weitere Aufgabentypen dazu in (7.2) und (7.3). Übung (9.7) bis (9.8): Textaufgaben mit Sinussatz lösen. Vermessungen. Level 2-3 Übung (9.9): Mit welchem Satz kann man die fehlenden Maße berechnen, mit dem Sinussatz oder Pythagoras oder sin/cos im rechtwinkligen Dreieck. Training der Lösungsstrategien. Sehr gut gemacht! Übung (9.10): Kann man mit diesen Maßen überhaupt ein Dreieck konstruieren? Anwendung vom Sinussatz. Übung und Tests (9.11) bis (9.14) nach Zufallsprinzip. Level 1-3 Cosinussatz – Berechnung an beliebigen Dreicken 10. Hier findest du reine Übungen zum Cosinussatz ( Übung (10.1) bis (10.8); aber auch eine Kombination von Sinussatz und Cosinussatz in den Übungen (10.9). bis (10.10). Mit Tests (10.11) bis (10.12) – Zufallsmischung Level 1-3. Bei realmath findest du weitere Übungen dazu in (8.1) bis (8.3) 11. Komplexere Aufgaben – Lösungsstrategien entwickeln Wann muss man mit dem Cosinussatz anfangen ? In welcher Reihenfolge kann man hier arbeiten? Und die restlichen Anwendungsaufgaben … das alles findest du hier in den Übungen (11.1) bis (11.8). 12. Winkel im Gradmaß und im Bogenmaß Übung (12.1) bis (12.19): Hier lernst du Winkel im Gradmaß und im Bogenmaß anzugeben bzw. von Grad in Bogenmaß umzuwandeln und umgekehrt. Es geht hier nur um Winkel, bis 360 ° und auch negative Winkel. 13. Sin / cos / tan von Winkeln im Bogenmaß bestimmen Übung (13.1) bis (13.6): Wie berechnet man – u.a. mit dem Taschenrechner- die Sinus, Cosinus- oder Tangenswerte von einem Winkel, der nicht in Grad, sondern im Bogenmaß angegeben ist? Nur Level 1, nur dieser Aufgabentyp. 14. Die Graphen von Sinus und Cosinus Übung (14.1) bis (14.8): Die Graphen von Sinus und Cosinus werden hier auf Periodizität, Symmetrie, Nullstellen und Extremstellen untersucht. Wie geht der Graph von der Cosinusfunktion aus dem Graphen der Sinusfunktion hervor? Übung (14.9): Eigenschaften des Graphen von sin und cos. Übung (14.10) bis (14.11): Einfache Gleichungen mit sin und cos lösen. Übung und Test (14.12) und (14.13): Zufallsmischung, Level 1 bis Level 3. 15. Der Graph von Tangens Hier findest du die gleichen Themen wie in (14), nur jetzt hier für die Tangensfunktion. Übung (15.1) bis (15.4): Der Graph von der Tangensfunktion wird auf Periodizität, Nullstellen, Definitionslücken und Symmetrie untersucht. Übung (15.5): Eigenschaften des Graphen der Tagensfunktion. Übung und Test (15.6) bis (15.8) zu (15.1) bis (15.5). Diese Spalte findest du rechts auf allen Seiten von realmath zum Sinus und Cosinus. Das ist so etwas wie eine ganz spezielle Menüleiste, hier gelangst du auch durch ein einfaches Anklicken auf weitere interessante Seiten zu diesen Themen. 1. Einheitskreis: Einführung und Zusammenhänge von sin/cos/tan (1.1) Für Sinus und Cosinus: Hier kannst du dir selbst deinen gewünschten Winkel im Einheitskreis erzeugen, indem du einfach den Punkt auf dem Einheitskreis weiter bewegst. Das ist toll! http://www.realmath.de/Neues/Klasse10/trigo/eisico.php (1.2) Für Tangens – auch so topp gemacht wie mit sinus /cosinus, unbedingt testen! http://www.realmath.de/Neues/Klasse10/trigo/eitan.php (1.3) Grundlegende Zusammenhänge zwischen sinus, cosinus und tangens, am Einheitskreis. http://www.realmath.de/Neues/Klasse10/trigo/supplement.php 2. Gesucht : die Winkel zu einem vorgegebenen Sinus-/Cosinus-/ oder Tangenswert (2.1) Sinuswerte: http://www.realmath.de/Neues/Klasse10/tangens/goniosin01.html http://www.realmath.de/Neues/Klasse10/tangens/goniosin.html (2.2) Cosinuswerte: http://www.realmath.de/Neues/Klasse10/tangens/goniocos01.html http://www.realmath.de/Neues/Klasse10/tangens/goniocos.html (2.3) Tangenswerte http://www.realmath.de/Neues/Klasse10/tangens/goniotan01.html http://www.realmath.de/Neues/Klasse10/tangens/goniotan.html (2.4) Variable Übung: Alle drei gemischt http://www.realmath.de/Neues/Klasse10/tangens/goniovar.html 3. Besondere Winkelmaße bei Sinus und Cosinus 30°, 45° und 60° (3.1) Sinus und Cosinus von 30 ° http://www.realmath.de/Neues/Klasse10/trigonometrie/besonderewinkel30.html (3.2) … von 45 ° http://www.realmath.de/Neues/Klasse10/trigonometrie/besonderewinkel45.html (3.3) … von 60 ° http://www.realmath.de/Neues/Klasse10/trigonometrie/besonderewinkel60.html 4. Tangens am Einheitskreis und über die Steigung einer Geraden (4.1) Einheitskreis: http://www.realmath.de/Neues/Klasse10/tangens/tangenssteigung.html (4.2) Punktsteigungsform der Geradengleichung und der Tangens http://www.realmath.de/Neues/Klasse10/tangens/tansteigueb.html (4.3) Geradengleichung und Schnittwinkel von Gerade und x-Achse http://www.realmath.de/Neues/Klasse10/tangens/mundtan.html (4.4) Polarkoordinaten und kartesiche Koordinaten – interessant für Tüftler http://www.realmath.de/Neues/Klasse10/polar/polarkoordinaten.html 5. Im rechtwinkligen Dreieck (5.1) Einführung im rechtwinkligen Dreieck am Einheitskreis/Strahlensatz http://www.realmath.de/Neues/10zwo/trigo/sinuseinf.html Sinus http://www.realmath.de/Neues/10zwo/trigo/kosinuseinf.html Cosinus http://www.realmath.de/Neues/10zwo/trigo/tangenseinf.html Tangens (5.2) Anwendung im rechtwinkligen Dreieck - d.h. die richtigen Gleichungen aufstellen http://www.realmath.de/Neues/10zwo/trigo/sinus.html für Sinus http://www.realmath.de/Neues/10zwo/trigo/kosinus.html für Cosinus http://www.realmath.de/Neues/10zwo/trigo/tangens.html für Tangens (5.3) Mischung aus sin, cos und tan - die richtigen Gleichungen aufstellen http://www.realmath.de/Neues/10zwo/trigo/winkelfunktionen.html http://www.realmath.de/Neues/10zwo/trigo/winkelfunktionen2.html http://www.realmath.de/Neues/10zwo/trigo/winkelfunktionen3b.html 6. Formel für den Flächeninhalt eines Dreiecks mit Nutzung vom Sinus (6.1) Herleitung der Formel für die verschiedenen Grundseiten a,b und c http://www.realmath.de/Neues/10zwo/trigo/trigodreieckflach.html http://www.realmath.de/Neues/10zwo/trigo/trigodreieckflach2.html http://www.realmath.de/Neues/10zwo/trigo/trigodreieckflach3.html (6.2) Anwendung der Formel → Flächeninhalt berechnen http://www.realmath.de/Neues/10zwo/trigo/dreiecktrigo.html 7. Sinus in beliebigen Dreiecken → Sinussatz (7.1) Herleitung http://www.realmath.de/Neues/10zwo/sinsatz/sinussatz.html (7.2) Anwendung des Sinussatzes für WSW – Übung http://www.realmath.de/Neues/10zwo/sinsatz/sinsatzaufg01.html http://www.realmath.de/Neues/10zwo/sinsatz/sinsatzaufg01.html (7.3) Anwendung des Sinussatzes für die SsW – Übung http://www.realmath.de/Neues/10zwo/sinsatz/sinsatzaufg01.html Vgl. bei bettermarks Abschnitt (9). 8. Cosinus in beliebigen Dreiecken → Cosinussatz (8.1) Cosinussatz SWS Übung http://www.realmath.de/Neues/10zwo/kosinussatz/kosinussatz2.html (8.2) Cosinussatz SSS-Übung http://www.realmath.de/Neues/10zwo/kosinussatz/kosinussatz.html (8.3) Weitere Übung http://www.realmath.de/Neues/Klasse10/trigo/kossatz2.html (8.4) Geometrische Veranschaulichung: der Cosinussatz als Verallgemeinerung des Pythagoras http://www.realmath.de/Neues/Klasse10/trigo/kosinusflaeche.html 9. Die Funktionsgraphen der trigonometrischen Funktionen (9.1) Die Funktion am Einheitskreis erklärt – topp! http://www.realmath.de/Neues/Klasse10/trifkt/sinusfunktion.html sin x http://www.realmath.de/Neues/Klasse10/trifkt/cosinusfunktion.html cos x http://www.realmath.de/Neues/Klasse10/trifkt/tangensfunktion.html tan x (9.2) Veränderungen der einfachen Funktionsgraphen http://www.realmath.de/Neues/Klasse10/trifkt/sinusfunktionvar.html y= a * sin(x-b) + c http://www.realmath.de/Neues/Klasse10/trifkt/cosinusfunktionvar.html y= a* cos(x-b) +c http://www.realmath.de/Neues/Klasse10/trifkt/tangensfunktionvar.html y= a* tan(x-b) + c 10. Herleitung der Additionstheoreme (10.1) des Sinus http://www.realmath.de/Neues/Klasse10/additionstheoreme/sinaddtheorem.html (10.2) des Cosinus http://www.realmath.de/Neues/Klasse10/additionstheoreme/cosaddtheorem.html