Allgemeine Lösungsbeschreibung

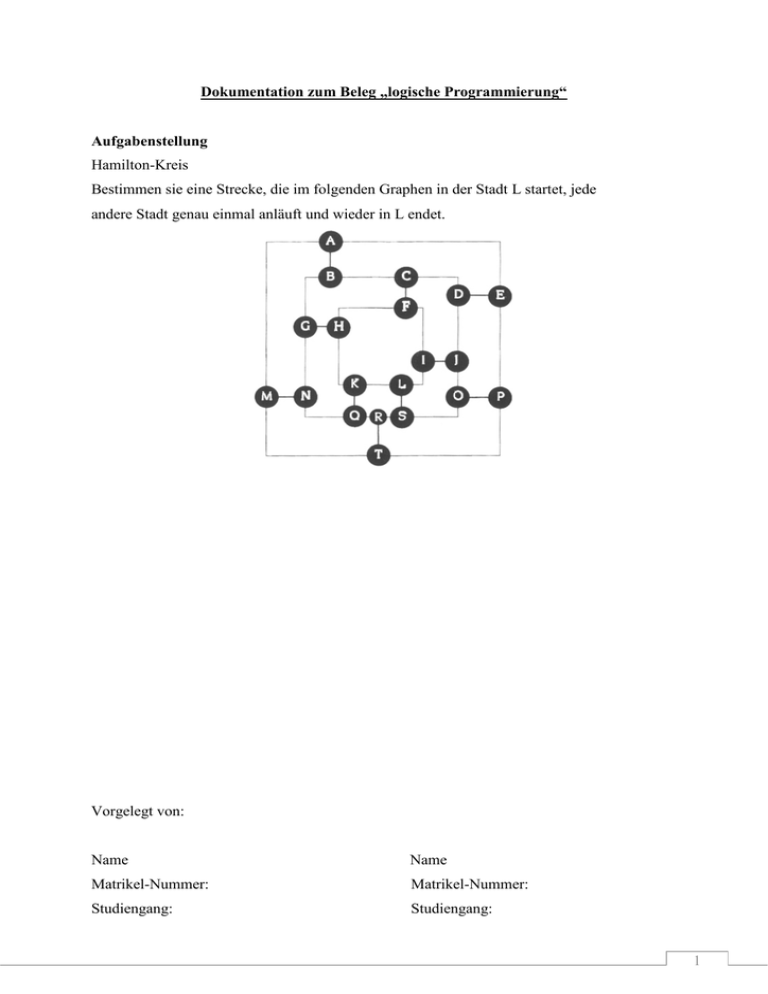
Dokumentation zum Beleg „logische Programmierung“
Aufgabenstellung
Hamilton-Kreis
Bestimmen sie eine Strecke, die im folgenden Graphen in der Stadt L startet, jede
andere Stadt genau einmal anläuft und wieder in L endet.
Vorgelegt von:
Name
Name
Matrikel-Nummer:
Matrikel-Nummer:
Studiengang:
Studiengang:
1
Hamilton-Kreis (hamilton.pl)
Algorithmus
Ziel des Hamilton-Zyklus ist es, in einem gegebenen Graphen einen Weg zu finden, bei dem
alle vorhandenen Knoten genau einmal berührt werden und an dessen Ende man sich wieder
im Ausgangsknoten befindet.
Um das zu erreichen, wird zuerst definiert, was ein Weg ist. Ein Weg muss aus einem
Startpunkt, dem Zielpunkt und der zurückgelegten Strecke bestehen. In unserem Fall besteht
die Strecke aus der Liste der berührten Knoten. Dieser Liste wird nun ausgehend vom
Zielknoten immer wieder ein neuer Knoten hinzugefügt und zwar so, dass dieser über eine
Kante mit dem vorhergehenden Knoten verbunden und außerdem noch nicht in der Liste
vorhanden ist. Sind diese Kriterien erfüllt, wird der neue Knoten der Liste hinzugefügt und
ein nächster Knoten gesucht. Falls der Startpunkt als nächster Knoten in Frage kommt, wird
er noch vorn hinzugefügt und es befinden sich alle Punkte vom Startpunkt bis zum Zielpunkt
in richtiger Reihenfolge in der Liste.
Nach dem Konsultieren des Prolog-Quelltextes und der Eingabe von „loesung.“ beginnt der
Algorithmus, die Aufgabe zu lösen. Es werden alle Wege vom Knoten „l“ zu all seinen
Nachbarknoten gefunden und darauf überprüft, ob sie die Länge 20 haben. Da jeder Knoten
nur ein Mal in einem Weg vorkommt, sind so alle Knoten enthalten. (Alternativ könnte man
hier jeden Knoten als Startpunkt nehmen, da alle Knoten im Weg vorkommen - das bringt
jedoch nichts, weil jeder andere Knoten ebenfalls 3 Nachbarn hat.) Mittels „findall“ werden
diese Wege nacheinander in eine Liste gespeichert. Da nun jede Route vor- und rückwärts
enthalten ist, werden diese Wiederholungen noch herausgefiltert.
Jedem einzelnen Weg wird der „l“-Knoten angefügt (vom Nachbarknoten aus ist „l“ einfach
zu erreichen) damit die Wege zueinander symmetrisch sind und mittels reverse/2 einfach
umgedreht werden können. Jeder Weg wird nun in der umgedrehten Reihenfolge der
enthaltenen Knoten in eine Liste aufgenommen und als Lösungsstrecke ausgegeben, sollte er
nicht schon in dieser Prüfliste enthalten sein.
[eine detailliertere Erklärung des Algorithmus‘ befindet sich innerhalb der Quelltext-Datei]
Datenstruktur
Die im Graphen enthaltenen Kanten wurden über das Prädikat „kante“(Knoten1, Knoten2)
definiert. Somit kann der gesamte Graph recht einfach modelliert werden, ohne komplizierte
Nachbarschaftsbeziehungen darzustellen.
Eine Alternative dazu war, die Kanten in einer Liste zu speichern. (siehe Optimierungen)
Der zurückgelegte Weg ist als Liste aller Wegknoten implementiert worden.
Optimierungen
Zuerst wurden die Kanten als Liste in die Datenbasis eingefügt. Eine einfache Darstellung als
Fakten erzeugte eine Reduktion der Inferenzen um den Faktor drei. Die globale Datenbasis
wird von PROLOG wesentlich effizienter durchsucht, als eine Liste. Die Implementierung als
Liste hatte den Grund, das Programm dynamischer bezüglich neuer „Schienennetze“ zu
machen, in dieser älteren Version des Programms wurden die Hamiltonwege zu einem
dynamisch zu findenden Nachbarknoten von „l“ gefunden, die die Länge der Kantenliste
2
hatten.
Sonst waren relativ wenige Optimierungen nötig, die zusammen etwa 2‘000 von 1‘300‘000
Inferenzen eingespart hatten.
Verallgemeinerung
Das Problem des Hamilton-Zyklus lässt sich auf das „Salesman-Problem“ abbilden. Dabei
wird die optimale Route zwischen mehreren Standorten gesucht, ohne einen Ort zweimal
anfahren zu müssen und dabei wieder am Startort anzukommen, beispielsweise um Waren aus
einem Lager auszuliefern.
Ebenfalls könnte man mit diesem Zyklus ein Token-Ring-Netzwerk aufbauen, bei dem die
Rechner örtlich etwas weiter auseinander stehen. Der Weg des Tokens kann anhand des
Hamilton-Zyklus bestimmt werden.
Programmcode
Anbei folgender Prolog-Quelltext:
hamilton.pl
Eingabe von loesung. erzeugt formatierte Ausgabe der 30 Lösungswege
(benötigt 1,131,981 Inferenzen)
3