Übungsklausur zur Experimentellen Mechanik - Heinrich

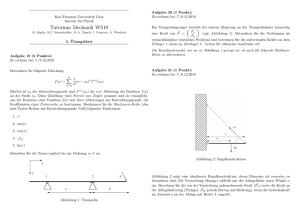
Instituts für Laser und Plasmaphysik Heinrich-­‐Heine-­‐Universität Prof. Dr. O. Willi Name: MatrNr.: Übungsklausur zur Experimentellen Mechanik 19.12.2012 Allgemeine Hinweise: Wenn nötig, nutzen Sie bitte für die Erdbeschleunigung g = 9, 81 m/s2. Ein Taschenrecher ist erlaubt, aber KEINE SMARTPHONES, Tablets, Kindles etc... (oder alles was Internet hat). Das Nachschlagen im Skript/Übungsblätter/Notizen/Formelsammlungen ist verboten. Jede Aufgabe ist auf einem gesonderten Blatt zu lösen, auf dem nochmals Name und Matrikelnummer aufgeschrieben werden müssen. Papier, Schmierzettel und Büroklammern werden bereitgestellt. Aufgabe 1 Kinematik/Dynamik des Massenpunktes (4 Pkt) (a) Eine Bowlingkugel, die mit konstanter Geschwindigkeit rollt, trifft die Kegel am Ende einer 16,5 m langen Bowlingbahn. Der Bowlingspieler hört das Geräusch, mit dem der Ball die Kegel trifft, 2,50 s nachdem er die Kugel losgelassen hat. Welche Geschwindigkeit hat die Kugel? Die Geschwindigkeit des Schalls beträgt 340 m/s. (b) Ein 75 m langer Zug beschleunigt gleichmäßig aus dem Stillstand. Wenn das vordere Ende des Zuges an einem Bahnarbeiter mit 25 m/s vorbeifährt, der sich 140 m weiter am Gleis gegenüber des Startpunkts befindet, wie groß ist dann die Geschwindigkeit des letzten Wagens, wenn dieser den Arbeiter passiert (Hinweis: berechnen Sie die Beschleunigung des Zuges und eliminieren Sie die Zeit)? Aufgabe 2 Kinematik/Gravitationsgesetz (4 Pkt) Ein Stuntfahrer möchte mit seinem Motorad über 8 nebeneinander unterhalb einer horizontalen Rampe geparkte Autos springen. (a) Mit welcher Mindestgeschwindigkeit muss er von der horizontalen Rampe abspringen? Die vertikale Höhe der Rampe beträgt 1,5 m über den Autos und der Stuntman muss einen horizontalen Weg von 20 m überspringen. (b) Wie groß muss die neue Mindestgeschwindigkeit des Motorads sein, wenn die Rampe nun nach oben gerichtet ist, so dass der „Absprungwinkel“ 10◦ über der Horizontalen beträgt, und sonst nichts geändert wurde? Aufgabe 3 Inertialkräfte/Gravitationskraft/Arbeit (6 Pkt) (a) Ein Jetpilot macht mit seinem Flugzeug einen senkrechten Looping. Bestimmen Sie den Mindestradius des Kreises, so dass die Beschleunigung im niedrigsten Punkt nicht größer ist als 6 g, wenn der Düsenjet mit einer Geschwindigkeit von 700 km/h im niedrigsten Punkt der Schleife fliegt. (b) Ein Satellit mit der Masse von 1 t wird in einer geostationären Umlaufbahn geschossen. Berechnen Sie die Höhe der Umlaufbahn. Die Masse der Erde beträgt 5,97 x1024 kg. Die Gravitationskonstante beträgt 6.67 x 10-­‐11 / (m3 kg-­‐1 s-­‐2) (Hinweis: auf einer geostationären Umlaufbahn dreht sich das Objekt gleich schnell wie die Erde, benutzen Sie ω=2π/T, T= 1 Tag) (c) Welche Arbeit muss gegen die Gravitation verrichtet werden, um den Satelliten in einer geostationären Umlaufbahn zu schießen? R_Erde = 6370 km Aufgabe 4 Reibungskraft/Newton’sche Gesetze (4 Pkt) Ein Rundfunktechniker errichten einen Fernmeldeturm, der 18 m hoch ist. Bei der kompletter Lösungsweg
Aufstellung stabilisieren sie den Turm mit 30 m langen Seilen, die von der Turmspitze bis zum Boden reichen. Die Verankerungen bestehen aus Betonblöcken, an denen die Seile befestigt werden können. Jeder Block wiegt 1600 N. Wie groß kann die maximale gerichteten WinVernachlässigen Sie dabei die Reibung und den LuftwiZugkraft in einem sein, bevor das Risiko dass sich die Verankerung des derstand.
(b)Seil Bestimmen
Sie den
Weg
s bis entsteht, zu der Stelle,
er 165 m hohen
Seils löst, wenn die CHaftreibungszahl zwischen einem Block und dem Boden 0,80 an der
sie bei
auf dem Boden aufkommt.
on 180 m/s abgebeträgt? keit des Geschosschlägt (Wenden
78 Wiederholen Sie Aufgabe 77, aber nehmen Sie jetzt an,
die Skispringerin bei Erreichen von Punkt
nach
Aufgabe dass
5 Energieerhaltung/Impulserhaltung (6 PBkt) oben
abspringt
und
eine
vertikale
Geschwindigkeits Weitsprung von
(bei B)
erreicht.
Ein Ball komponente
mit der Masse m1von
ist 3,0
an m/s
einem horizontalen Seil mit der Länge L befestigt, pielen 1936 kann
dessen anderes Ende fixiert ist, (siehe Abb. 1.) elpunkt vom Ab79Welche Ein Ball
ist an einem horizontalen
Seilim mittiefsten der Länge
ჼ (a) Geschwindigkeit hat der Ball Punkt seines Weges, wenn er höchsten Punkt
L
befestigt,
dessen
anderes
Ende
fixiert
ist,
Abbillosgelassen wird? Mindestgeschwin(a) Welche
hat der Ball
im
(b) Ein dung
Stift 8.36.
befindet sich Geschwindigkeit
in einem bestimmten Abstand h direkt unterhalb des igte, wenn er an
tiefsten Punkt seines Weges, wenn er losgelassen wird?
Geschwindigkeit
Befestigungspunktes des Seils. Wie groß ist die Geschwindigkeit des Balls, wenn er den (b) Ein Stift befindet sich in einem bestimmten Abstand
obersten Punkt seiner kreisförmigen Bahn um den Stift herum erreicht, wenn h = 0,80L h direkt unterhalb des Befestigungspunktes des Seils.
ist? inen Berg mit eiWie groß ist die Geschwindigkeit des Balls, wenn er
(c) Falls der Ball m
1 auf einem zweiten Ball mit der Masse m
fahren, um eine
den obersten
Punkt seiner kreisförmigen Bahn um den 2 elastisch stöß, welcher in Ruhe vertikal an einem mit der Länge L hängt (siehe Abb. 2. ), halten? VernachStift herum erreicht, zweiten wenn h =Faden 0,80L ist?
beschreiben Sie was passieren wird für die Fälle m1/m2 <<1, m1/m2 =1, und m1/m2 >> 1. Sie an, dass die
gt.
gangsleistung eie vertikale Höhe
n 0,20 kg fällt von
Boden befindet.
de er auf dem Bond vernachlässigt
urchschnittliche
Abb. 1.
standes, wenn er
von 10,0 m/s auf
n 60 kg startet aus
nze, im Punkt A
Rampe hinunter.
Stift
Abb. 2.
Abbildung 8.36 Aufgaben 79 und 80.
80 Zeigen Sie, dass der Ball in Abbildung 8.36 nur dann
einen kompletten Kreis um den Stift beschreiben kann,
wenn h ≥ 0,60L ist.