Tutorium Mechanik WS10 - Website von Andreas Windisch.

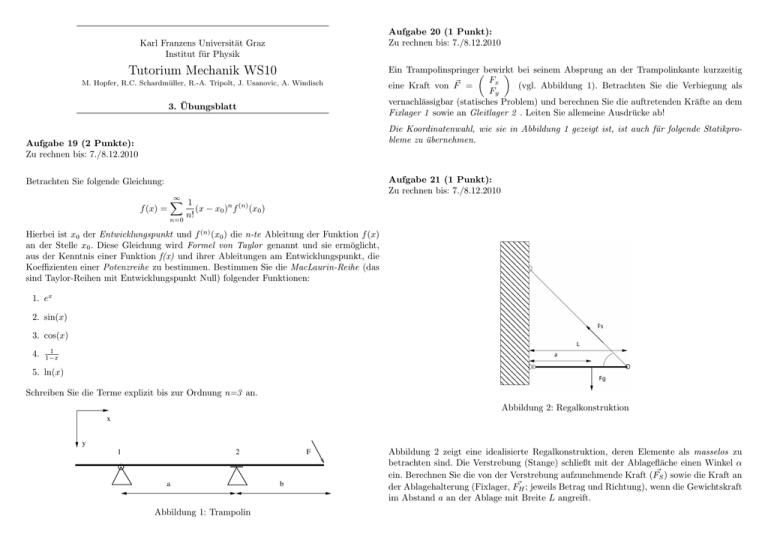
Aufgabe 20 (1 Punkt):
Zu rechnen bis: 7./8.12.2010
Karl Franzens Universität Graz
Institut für Physik
Tutorium Mechanik WS10
M. Hopfer, R.C. Schardmüller, R.-A. Tripolt, J. Usanovic, A. Windisch
3. Übungsblatt
Ein Trampolinspringerbewirkt
bei seinem Absprung an der Trampolinkante kurzzeitig
F
x
eine Kraft von F~ =
(vgl. Abbildung 1). Betrachten Sie die Verbiegung als
Fy
vernachlässigbar (statisches Problem) und berechnen Sie die auftretenden Kräfte an dem
Fixlager 1 sowie an Gleitlager 2 . Leiten Sie allemeine Ausdrücke ab!
Die Koordinatenwahl, wie sie in Abbildung 1 gezeigt ist, ist auch für folgende Statikprobleme zu übernehmen.
Aufgabe 19 (2 Punkte):
Zu rechnen bis: 7./8.12.2010
Aufgabe 21 (1 Punkt):
Zu rechnen bis: 7./8.12.2010
Betrachten Sie folgende Gleichung:
f (x) =
∞
X
1
(x − x0 )n f (n) (x0 )
n!
n=0
Hierbei ist x0 der Entwicklungspunkt und f (n) (x0 ) die n-te Ableitung der Funktion f (x)
an der Stelle x0 . Diese Gleichung wird Formel von Taylor genannt und sie ermöglicht,
aus der Kenntnis einer Funktion f(x) und ihrer Ableitungen am Entwicklungspunkt, die
Koeffizienten einer Potenzreihe zu bestimmen. Bestimmen Sie die MacLaurin-Reihe (das
sind Taylor-Reihen mit Entwicklungspunkt Null) folgender Funktionen:
1. ex
2. sin(x)
3. cos(x)
4.
1
1−x
5. ln(x)
Schreiben Sie die Terme explizit bis zur Ordnung n=3 an.
Abbildung 2: Regalkonstruktion
x
y
1
2
a
Abbildung 1: Trampolin
F
b
Abbildung 2 zeigt eine idealisierte Regalkonstruktion, deren Elemente als masselos zu
betrachten sind. Die Verstrebung (Stange) schließt mit der Ablagefläche einen Winkel α
ein. Berechnen Sie die von der Verstrebung aufzunehmende Kraft (F~S ) sowie die Kraft an
der Ablagehalterung (Fixlager, F~H ; jeweils Betrag und Richtung), wenn die Gewichtskraft
im Abstand a an der Ablage mit Breite L angreift.
Aufgabe 22 (2 Punkte):
Zu rechnen bis: 10.12.2010
2. Eine U-Bahn wird durch eine Notbremsung innerhalb von 20 s auf einer Strecke
von 400 m zum Stehen gebracht. Der Bremsvorgang kann als konstante Verzögerung
(=negative Beschleunigung) betrachtet werden.
(a) Welche Reisegeschwindigkeit hatte der Zug vor der Notbremsung?
(b) Wie groß war seine Bremsverzögerung?
3. Auto A fährt mit einer konstanten Geschwindigkeit von 20 m/s hinter Auto B her,
das eine ebenfalls konstante Geschwindigkeit von 12 m/s hat.
(a) Wie lange benötigt Auto A um Auto B einzuholen?
(b) Welchen Weg legt Auto A dabei zurück, wenn der anfängliche Abstand 600 m
beträgt?
Abbildung 3: An einer Mauer lehnende Leiter
Aufgabe 24 (1 Punkt):
Zu rechnen bis: 10.12.2010
Gegeben sei die in Abbildung 3 schematisch angedeutete Situation einer 9 kg schweren Ein Ball wird senkrecht nach oben geworfen und trifft nach 2, 04 s wieder am Boden auf.
und 5 m langen Leiter, die an einer Wand lehnt. Die Leiter kann reibungsfrei an der
1. Wie hoch war seine Anfangsgeschwindigkeit?
Wand gleiten (vgl. Gleitlager), zwischen dem anderen Ende und dem Boden gelte jedoch
ein Haftreibungskoeffizient von µH = 0, 3. (Es gilt: max (FR,tangential ) = µH · Fnormal ,
2. Berechnen Sie seine maximale Wurfhöhe.
siehe hierzu VO Skriptum, Reibung).
3. Welche Geschwindigkeit hat er in einer Höhe von 1, 8 m?
1. Bis zu welchem Winkel zwischen Boden und Leiter θmin kann die Leiter angelehnt
werden, ohne wegzurutschen?
4. Zeichnen Sie das Höhe-Zeit-Diagramm.
Aufgabe 25 (1 Punkt):
2. Das untere Ende der Leiter befindet sich fix in einem Abstand von x = 3m zur Wand. Zu rechnen bis: 10.12.2010
Zeichnen Sie eine Skizze mit allen wirkenden Kräften (auf die Richtung achten) und
berechnen Sie diese. Geben Sie zunächst allgemeine Formeln an und setzen Sie erst
Ein Fußballspieler sieht, dass der gegnerische Tormann 10m vor dem Tor steht. Er überlegt
anschließend die Werte mit Einheit ein.
nicht lange und setzt 30 m vor dem Tor zu einem Weitschuß an. Der Ball verlässt seinen
Fuß unter einem Winkel von 30◦ zum Rasen und einer Anfangsgeschwindigkeit von 20m/s.
Aufgabe 23 (2 Punkte):
Zu rechnen bis: 10.12.2010
Geben Sie bei den nachfolgenden Beispielen zunächst (eine) allgemeine Lösung(en) an
und setzen sie anschließend die Werte mit zugehörigen Einheiten ein!
1. Die Geschwindigkeit des Lichts beträgt etwa 3 · 108 m/s. Die Schallausbreitungsgeschwindigkeit beträgt etwa 333 m/s. Bei einem Gewitter werde der Donner an einem
bestimmten Ort 13, 5 s später registriert als der Blitz. Wie groß ist die Entfernung
des Blitzeinschlages vom Beobachtungsort?
1. Welche Höhe erreicht der Ball maximal?
2. In welcher Entfernung vom Abschusspunkt trifft der Ball wieder auf den Boden?
3. Kann der Tormann den Ball ablenken, wenn er im Sprung eine Höhe von 3m erreicht?