Tutorium Mechanik WS10 - Website von Andreas Windisch.

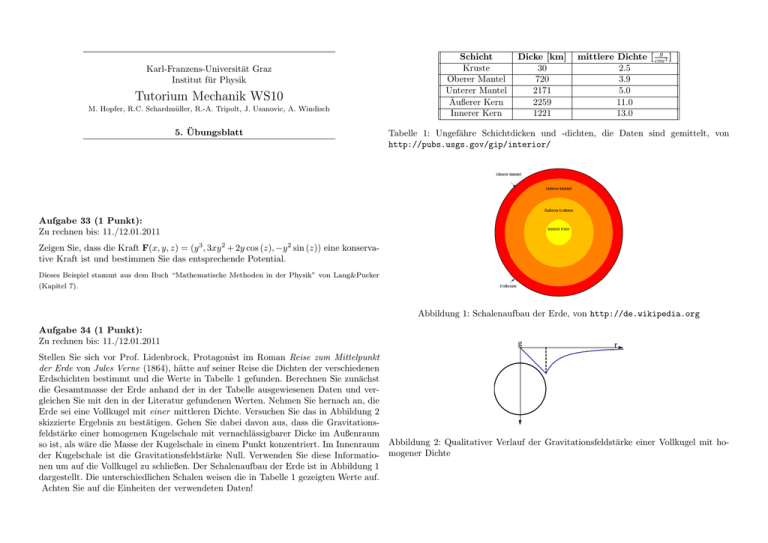
Karl-Franzens-Universität Graz
Institut für Physik
Tutorium Mechanik WS10
M. Hopfer, R.C. Schardmüller, R.-A. Tripolt, J. Usanovic, A. Windisch
5. Übungsblatt
Schicht
Kruste
Oberer Mantel
Unterer Mantel
Äußerer Kern
Innerer Kern
Dicke [km]
30
720
2171
2259
1221
g
mittlere Dichte [ cm
3]
2.5
3.9
5.0
11.0
13.0
Tabelle 1: Ungefähre Schichtdicken und -dichten, die Daten sind gemittelt, von
http://pubs.usgs.gov/gip/interior/
Aufgabe 33 (1 Punkt):
Zu rechnen bis: 11./12.01.2011
Zeigen Sie, dass die Kraft F(x, y, z) = (y 3 , 3xy 2 + 2y cos (z), −y 2 sin (z)) eine konservative Kraft ist und bestimmen Sie das entsprechende Potential.
Dieses Beispiel stammt aus dem Buch “Mathematische Methoden in der Physik” von Lang&Pucker
(Kapitel 7).
Abbildung 1: Schalenaufbau der Erde, von http://de.wikipedia.org
Aufgabe 34 (1 Punkt):
Zu rechnen bis: 11./12.01.2011
g
r
Stellen Sie sich vor Prof. Lidenbrock, Protagonist im Roman Reise zum Mittelpunkt
der Erde von Jules Verne (1864), hätte auf seiner Reise die Dichten der verschiedenen
Erdschichten bestimmt und die Werte in Tabelle 1 gefunden. Berechnen Sie zunächst
die Gesamtmasse der Erde anhand der in der Tabelle ausgewiesenen Daten und vergleichen Sie mit den in der Literatur gefundenen Werten. Nehmen Sie hernach an, die
Erde sei eine Vollkugel mit einer mittleren Dichte. Versuchen Sie das in Abbildung 2
skizzierte Ergebnis zu bestätigen. Gehen Sie dabei davon aus, dass die Gravitationsfeldstärke einer homogenen Kugelschale mit vernachlässigbarer Dicke im Außenraum
so ist, als wäre die Masse der Kugelschale in einem Punkt konzentriert. Im Innenraum Abbildung 2: Qualitativer Verlauf der Gravitationsfeldstärke einer Vollkugel mit hoder Kugelschale ist die Gravitationsfeldstärke Null. Verwenden Sie diese Informatio- mogener Dichte
nen um auf die Vollkugel zu schließen. Der Schalenaufbau der Erde ist in Abbildung 1
dargestellt. Die unterschiedlichen Schalen weisen die in Tabelle 1 gezeigten Werte auf.
Achten Sie auf die Einheiten der verwendeten Daten!
Aufgabe 35 (1 Punkt):
Zu rechnen bis: 11./12.01.2011
Lösen Sie folgende Aufgaben:
(a) Berechnen Sie die Umlaufzeit des Saturnmondes Mimas, dessen mittlerer Bahnradius 1.86 × 108 m beträgt.
(b) Berechnen Sie den mittleren Bahnradius des Mondes Titan, der den Saturn in
einer Zeit von 1.38 × 106 s umkreist.
Überlegen Sie sich, welche Symmetrien bei diesem Problem vorliegen und rechnen Sie
mit den sich daraus ergebenden Erhaltungsgrößen, um zur Lösung zu gelangen. Bei der
Masse m könnte es sich zum Beispiel um eine kleine Kugel in einer stark gekrümmten
Schale im Schwerefeld der Erde handeln. Je nach Start-Drehimpuls bewegt sie sich
auf unterschiedlichen Bahnen, wobei nur eine bestimmte Bahn bei dieser Aufgabe von
Interesse ist.
HINWEIS: L = mrv = mr2 ω = mr2 ϕ̇ (vgl. Skriptum Knoll, S. 80f)
Die Saturnmasse beträgt MS = 5.69 × 1026 kg.
Aufgabe 39 (1 Punkt):
Zu rechnen bis: 14.01.2011
Aufgabe 36 (1 Punkt):
Zu rechnen bis: 11./12.01.2011
Das Methanmolekül (CH4) besteht aus 4 Wasserstoffatomen, die in den Eckpunkten eines Tetraeders mit der Seitenlänge 0.18nm angeordnet sind, und einem Kohlenstoffatom im Mittelpunkt des Tetraeders. Berechnen Sie das Trägheitsmoment
Im Apogäum (erdfernster Punkt der Umlaufbahn) ist der Erdmond 406 395 km und
im Perigäum (erdnächster Punkt der Umlaufbahn) 357 643 km von der Erde entfernt.
Seine Umlaufzeit beträgt T = 27.3 d.
Welche Geschwindigkeit hat der Mond im Perigäum und welche im Apogäum?
Aufgabe 37 (1 Punkt):
Zu rechnen bis: 14.01.2011
Der Asteroid Ikarus hat eine Exzentrizität von e = 0.83 und eine Umlaufzeit von
T = 1.1a (Jahren). Die Exzentrizität e, Entfernung zum Perihel rp und große Halbachse
a sind wie folgt verknüpft:
rp = a(1 − e)
Berechnen Sie die große Halbachse der Bahn von Ikarus und geben Sie die Entfernung
des Asteroiden von der Sonne im Perihel und im Aphel an.
Aufgabe 38 (2 Punkte):
Zu rechnen bis: 14.01.2011
Abbildung 3: Methanmolekül, von http://en.wikipedia.org
Eine Masse m bewegt sich in einem Zentralkraftfeld F(r) = −A r4 er mit einem zugehörigen Drehimpuls L. L und A seien positive Konstanten, er ist der Einheitsvektor des Moleküls bezüglich der z-Achse, gegeben durch den Mittelpunkt des Kohlenstofin radialer Richtung. Das Potential im Ursprung sei Null: U (0) = 0.
fatoms und den Mittelpunkt eines Wasserstoffatoms. (Masse des Wasserstoffatoms
MH = 1.67 × 10−27 kg)
(a) Für welche kinetische Energie bewegt sich das Teilchen auf einer Kreisbahn?
Optional : Schreiben Sie den Trägheitstensor (bezüglich der z-Achse) für das Molekül
(b) Wie groß ist der Radius dieser Kreisbahn?
an (für die nicht berechneten Komponenten können Sternchen eingetragen werden).
Aufgabe 40 (1 Punkt):
Zu rechnen bis: 14.01.2011
Lösen Sie folgende Aufgaben:
(a) Berechnen Sie das Trägheitsmoment eines aufgestellten Hohlzylinders mit der
Höhe h, dem Innenradius R1 und dem Außenradius R2 bezüglich der z-Achse
(Haupt-Symmetrieachse).
(b) Berechnen Sie mit dem Steinerschen Satz das Trägheitsmoment des selben
Körpers, allerdings ist die Haupt-Symmetrieachse nun um R1 /2 aus der Mitte
gerückt.
Aufgabe 41 (1 Punkt):
Zu rechnen bis: 14.01.2011
Berechnen Sie die kinetische Rotationsenergie der Erde bezüglich ihrer Drehachse und
vergleichen Sie diesen Wert mit der kinetischen Energie aufgrund der Bahnbewegung
der Erde (des Massenmittelpunktes) um die Sonne.
Nehmen Sie an, dass die Erde eine gleichförmige Kugel mit einer Masse von
ME = 6 × 1024 kg und einem Radius von RE = 6.4 × 106 m ist. Der Radius der als
kreisförmig angenommenen Erdbahn beträgt RB = 1.5 × 1011 m.