Zeitreihenanalyse Der einfache gleitende

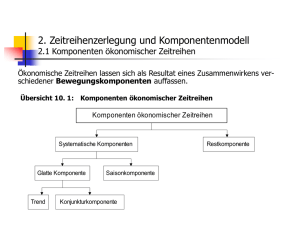
(c) Projekt Neue Statistik 2003 - Lernmodul: Zeitreihenanalyse Der einfache gleitende Durchschnitt
Zeitreihenanalyse Der einfache gleitende
Durchschnitt
Worum geht es in diesem Lernmodul?
Einleitung
Erläuterung der Methode
Berechnung des einfachen gleitenden Durchschnitts
Der einfache gleitende Durchschnitt mit gerader Länge
Glättung von Zeitreihen mit Saisonfigur
Verlust von Werten durch Glättung
Weiterführende Links
Worum geht es in diesem Lernmodul?
In diesem Lernmodul werden wir uns mit dem Verfahren des einfachen gleitenden
Durchschnitts befassen. Mit Hilfe von Beispielen werden die möglichen Anwendungen
des Verfahrens und Ihre Grenzen aufgezeigt. Die rechnerische Grundlage des
Verfahrens wird ausführlich erklärt. Im Rahmen der Übungen haben Sie Gelegenheit,
das Verfahren zu erproben.
Einleitung
Neben der im vorherigen Kapitel besprochenen Methode, die Trendkomponente einer
Zeitreihe durch eine Trendgerade oder ein Trendpolynom zu erfassen, gibt es die
Möglichkeit, die glatte Komponente einer Reihe mit Hilfe eines gleitenden
Durchschnittes zu bestimmen. Wir wollen uns dieses Verfahren an Hand eines
Beispieles ansehen.
Beispiel: Die Entwicklung der globalen Durchschnitts-temperatur
Seit geraumer Zeit steht die globale Erwärmung, also der Anstieg der bodennahen
Temperatur, im Mittelpunkt der öffentlichen Diskussion um die Veränderung unseres
Klimas. Die nachfolgende Grafik zeigt die Entwicklung der bodennahen
Jahresmitteltemperatur von 1866 bis 1996 in Grad Celsius.
Abb. TEMPERATUR 1: Die globale Durchschnittstemperatur
Quelle: Janacek, Gareth: Practical Time Series, London, Arnold 2001
Page 1
(c) Projekt Neue Statistik 2003 - Lernmodul: Zeitreihenanalyse Der einfache gleitende Durchschnitt
Der Verlauf der Zeitreihe ist sehr unruhig. Möchten wir trotzdem auf der Basis dieser
Daten die Frage beantworten, ob unser Klima wärmer geworden ist und wenn um wie
viel Grad, so ist es sinnvoll, die Zeitreihe zu glätten.
Beispiel:
Glättung mit Hilfe des einfachen gleitenden Durchschnittes
Zur Glättung der Reihe benutzen wir das arithmetische Mittel. Um nicht nur einen
einzigen Wert zu erhalten, berechnen wir nicht den Mittelwert der gesamten Reihe,
sondern bilden die Mittelwerte über gleichlange Teilstücke. In diesem Fall werden wir
jeweils das Mittel über 21 Werte berechnen, d.h. wir berechnen den Mittelwert der
ersten 21 Werte, dann den des 2. bis 22. Wertes, des 3. bis 23., des 4. bis 24. und sofort.
Die arithmetischen Mittel werden jeweils dem zeitlichen Mittelpunkt des Teilstücks
zugeordnet, d.h. der Mittelwert des ersten Teilstücks wird dem Zeitpunkt t=11, der des
2. Teilstücks dem Zeitpunkt t=12 , der des dritten Teilstücks dem Zeitpunkt t=13, usw.
zugeordnet.
Das Ergebnis ist die geglättet Zeitreihe der globalen Durchschnittstemperatur (roter
Linienzug in Abb.: TEMPERATUR 2).
Abb. TEMPERATUR 2: Ausgangsreihe (blau) und geglättete Reihe (rot) der globalen Durchschnittstemperatur
Quelle: Janacek, Gareth: Practical Time Series, London, Arnold 2001
Die Relevanz der Temperaturdaten ist nicht unumstritten. Nehmen wir aber die
vorliegenden Daten als Grundlage, so ist nach der Glättung deutlich eine Steigung von
ca. 0.6 Grad abzulesen. Dies entspricht der Einschätzung namhafter Wissenschaftler auf
dem Gebiet der Klimaforschung. [Kapala, 2002]
Erläuterung der Methode
Die im vorangegangenen Beispiel benutzte Methode des einfachen gleitenden
Durchschnitts wird zur Glättung von Zeitreihen benutzt. Glättung meint die
Ausschaltung von irregulären Schwankungen. Unter Annahme des klassischen
Komponentenmodells kommt dies der näherungsweisen Bestimmung der glatten
Komponente gleich.
Bei der Anwendung des einfachen gleitenden Durchschnitts wird für gleich lange
Zeitreihensegmente das zugehörige arithmetische Mittel berechnet und den jeweiligen
zeitlichen Mittelpunkten der Segmente zugeordnet. Diesen Zusammenhang
veranschaulicht die nachfolgende Animation.
: Flashanimation ' Animation Der einfache gleitende Durchschnitt ' siehe
Online-Version
Berechnung des einfachen gleitenden Durchschnitts
Die folgende Tabelle gibt einige Beispiele zur Berechnung einfacher gleitender
Durchschnitte mit ungerader Länge wieder:
Länge
Page 2
Formel
(c) Projekt Neue Statistik 2003 - Lernmodul: Zeitreihenanalyse Der einfache gleitende Durchschnitt
3
5
7
9
Die mathematische Formel zur Berechnung des einfachen gleitenden Durchschnitts
lautet:
Jeder Wert des Segmentes wird demzufolge gleich gewichtet, mit
.
Der Laufindex q lässt sich aus der für den einfachen gleitenden Durchschnitt gewählten
Segmentlänge, also der Anzahl der zur Mittelwertsbildung einbezogenen Werte
berechen:
.
In der Regel wird die Länge des einfachen gleitenden Durchschnittes ungerade gewählt.
Beispiel: Jährliche Konkurse in den USA
Die Ausgangszeitreihe in Abb. KONKURSE zeigt den prozentualen Anteil der jährlich
in Konkurs gegangenen Unternehmen an allen Unternehmen in den USA von 1867 bis
1932 (blauer Linienzug).
Die Zeitreihe (blauer Linienzug) wurde geglättet mit einfachen gleitenden
Durchschnitten der Länge drei (dunkelroter Linienzug), sieben (orange) und dreizehn
(türkis).
Abb. KONKURSE
Quelle: Rainer Schlittgen (1994)
Sie haben hier die Möglichkeit, das Verfahren des einfachen gleitenden Durchschnitts
an dem recht unruhigen Verlauf des Züricher Aktienindex zu erproben.
Labordatei öffnen ( aa3.spf )
Der einfache gleitende Durchschnitt mit gerader Länge
Wird der einfache gleitende Durchschnitt für eine gerade Anzahl von Werten bestimmt,
liegt der Segmentmittelpunkt zwangsläufig zwischen zwei Zeitpunkten. So müsste
beispielsweise der erste Wert, einer mit einem einfachen gleitenden Durchschnitt der
Länge vier geglätteten Zeitreihe, dem Zeitpunkt 2.5 zugeordnet werden:
Inhaltlich ist dies nicht sinnvoll, denn man enthält einen Wert für einen Zeitpunkt zu
dem nie gemessen wurde. Um das Problem zu umgehen, behilft man sich mit einem
kleinen Trick und erhöht die Segmentlänge um eins, lässt dafür aber die Randpunkte
nur mit halbem Gewicht eingehen.
Page 3
(c) Projekt Neue Statistik 2003 - Lernmodul: Zeitreihenanalyse Der einfache gleitende Durchschnitt
Beispiele einfacher gleitender Durchschnitte mit gerader Länge
Länge
Formel
2
4
6
8
Den Laufindex
berechnet sich in diesem Fall entsprechend aus der halben Länge
.
Glättung von Zeitreihen mit Saisonfigur
Liegt eine Zeitreihe mit Saisonkomponente vor, empfiehlt es sich die Länge des
einfachen gleitenden Durchschnitts entsprechend der einfachen oder mehrfachen
Periodendauer der Saison zu wählen. Die geglättete Zeitreihe weist dann keine
Saisonfigur mehr auf.
Beispiel: Umsatzzahlen mit Saisonfigur
Ein Einzelhändler hat 1987 ein Lebensmittelgeschäft übernommen. In den ersten drei
Jahren lief der Verkauf in den unveränderten Räumen. 1990 entschloss sich der Händler
zu einer Vergrößerung und Modernisierung der Verkaufräume. Jetzt liegen ihm die
Umsätze der letzten 15 Jahre vor (Abb. UMSATZ: blauer Linienzug).
Abb.UMSATZ
Fragestellung
Der Händler möchte die Entwicklung des Umsatzniveaus in den letzten 15 Jahren
abschätzen. Außerdem will er wissen, ob sich der Umbau auf die Verkaufszahlen
positiv ausgewirkt hat. Er plant zudem eine zweite Erweiterung seiner Ladenfläche und
würde daher gerne den zu erwartenden Umsatz prognostizieren.
Antwort
Zur Beantwortung dieser Fragen wird die Zeitreihe des Umsatzes mit einem einfachen
gleitenden Durchschnitt der Länge 24, der doppelten Periodenlänge, geglättet (Abb.
UMSATZ: roter Linienzug)
Wie in der Grafik gut zu sehen ist, wird dadurch die Saisonfigur beseitigt und die glatte
Komponente herausgearbeitet. Im Jahre 1987 beträgt der Umsatz im Mittel ca. 28.000
Euro und wächst auf ein Niveau von ca. 35.000 Euro im Jahre 2000. Deutlich ist ein
linearer Anstieg ab dem Jahr 1990/1991 zu erkennen. Wenn der steigende Umsatz nicht
Page 4
(c) Projekt Neue Statistik 2003 - Lernmodul: Zeitreihenanalyse Der einfache gleitende Durchschnitt
auf andere Einflüsse zurückgeführt werden kann, so war die Modernisierung der
Verkaufsfläche offensichtlich eine gute Entscheidung.
Zur Prognose der zukünftigen Umsätze ist der einfache gleitende Durchschnitt denkbar
ungeeignet. Die geglättete Zeitreihe enthält nur Werte bis zum Juni 2000. Der Zeitpunkt
zu dem der Händler die Zeitreihe betrachtet, ist aber der Juni 2001. Bedingt durch das
Konzept des gleitenden Durchschnitts und die hier gewählte Länge 24, fehlen die
letzten zwölf Werte. Auf dieser Grundlage eine Prognose zu wagen, wäre also eher
spekulativ.
Die Zeitreihe der Leistungsbilanz des Außenhandels zeigt deutlich eine Saisonfigur.
Beseitigen Sie diese mit Hilfe eines einfachen gleitenden Durchschnittes.
Labordatei öffnen ( b1e.spf )
Verlust von Werten durch Glättung
Bei der Glättung durch einen einfachen gleitenden Durchschnitt gehen an beiden
Rändern der Zeitreihe jeweils q Werte verloren. Das ist oft, wie im vorangegangenen
Beispiel, speziell für den aktuellen Rand der Zeitreihe, nicht akzeptabel. Die folgende
Animation im Statistiklabor verdeutlicht dieses Problem.
Labordatei öffnen ( b26.spf )
Weiterführende Links
Zeitreihen zum Üben und Ausprobieren:
vergleiche :
Chatfield, Christopher (1982). Analyse von Zeitreihen. München, Hanser.
Janacek, Gareth (2001). Practical Time Series. London, Arnold.
Schlittgen, Rainer (2001). Angewandte Zeitreihenanalyse. München; Wien,
Oldenbourg.
Schlittgen, R.; Streitberg, B.H.J. (2001).Zeitreihenanalyse . München; Wien,
Oldenbourg.
Kapala, A. (2002): Änderung der "globalen" Temperatur. Internet:
(c) Projekt Neue Statistik 2003, Freie Universität Berlin, Center für Digitale Systeme
Kontakt: http://www.neuestatistik.de
Page 5