nichtstationaritaet

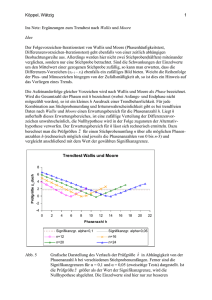
4. Nichtstationarität und Kointegration
4.1 Einheitswurzeltests (Unit-Root-Tests)
Spurious regression
In einer Simulationsstudie haben Granger und Newbold (1974) aus zwei unabhängigen Random Walks (Unit-Root-Prozesse)
(4.1) X t  X t 1  1t
und
(4.2) Yt  Yt 1  2t
in der (ε1t) und (ε1t) unabhängige White-Noise-Prozesse sind, ein Regressionsmodell gebildet
(4.3) Yt  ß0  ß1  Xt  Ut
Bei den Simulationen stellte sich heraus, dass die Nullhypothese
H0: ß1 = 0
bei einem Signifikanzniveau  von 5% in ca. 75% der Fälle abgelehnt werden
musste. Außerdem nahm das Bestimmtheitsmaß R² hohe Werte an, während
die Residuen autokorreliert waren.
Substanziell lassen sich die Signifikanz und hohe Bestimmheit jedoch nicht
interpretieren, da die Regression aus unabhängigen Prozessen gebildet
worden ist. Der scheinbare Zusammenhang („spurious regression“) ist ein
Artefakt der Nichtstationarität.
:
Dickey-Fuller-Tests und Integrationsordnung
Mit Hilfe von Dickey-Fuller-Tests können Variablen (Zeitreihen) auf Nichtstationarität getestet werden. Wie bereits bei den ARIMA-Modellen erörtert, können
nichtstationäre Variablen mit stochastischen Trends durch Differenzenbildung
(„Differenzierung“) in stationäre Variablen überführt werden.
Kann eine nichtstationäre Zeitreihe (yt) nach einfacher Differenzenbildung in
eine stationäre Reihe überführt werden, ist sie integriert von der Ordnung 1:
Yt  I(1).
Allgemein ist eine Zeitreihe (yt) integriert von der Ordnung d,
Yt  I(d),
falls sie nach d-maliger Anwendung des Differenzenoperators  stationär wird.
Eine stationäre Reihe (yt) ist integriert von der Ordnung 0: Yt  I(0).
Die Dickey-Fuller-Tests geben Aufschluss über die Ordnung der Integration
von Variablen (Zeitreihen), womit sie gleichzeitig anzeigen, ob eine Reihe stationär
oder nichtstationär ist.
Trendstationarität und Differenzenstationarität
Teststrategie von Elder und Kennedy (2001) bei Anwendung des Dickey-Fuller-Tests (DFTest) zur Überprüfung einer Zeitreihe (yt) auf Nichtstationarität:
Ausnutzung theoretischer und empirischer Erkenntnisse (z.B. Zeitreihendiagramm), um die
Zeitreihe als langfristig wachsend oder nicht wachsend zu bezeichnen.
Beispiel:
- Zeitreihen des BIP, des Einkommens, des Konsums wachsen im Zeitverlauf
- Zeitreihen der Zinssätze, Inflationsraten, Arbeitslosenquoten folgen langfristig keinem
Wachstumstrend
Bei langfristig wachsenden Zeitreihen bleibt die Frage offen, ob die Zeitreihenwerte yt durch
einen deterministischen Trend wie z.B. mt = α + β · t und einer Überlagerung von WhiteNoise-Störgrößen Ut ,
(4.4)
Yt      t  Ut ,   0,
oder aber durch einen stochastischen Trend der Form
(4.5)
Yt    Yt 1  Ut ,   0,
erzeugt werden.
Wie sich zeigt, unterscheiden sich die Prozesse (4.4) und (4.5) fundamental voneinander.
Gleichung (4.4): Trendstationärer Prozess
Gleichung (4.5): Differenzstationärer Prozess
Trendstationärer Prozess
Y(t)
24
Trendstationärer Prozess: Y(t)=1 + 0.2*t + U(t)
(Ut):White-Noise-Prozess
mit E(Ut) = 0 und Var(Ut) = 3
20
16
12
8
4
0
10
20
30
40
50
60
70
80
90
100 t
Trendstationärer Prozess (4.4):
Erwartungswert: E(Yt )      t
Der deterministische Trend wird durch zufällige Abweichungen überlagert, die durch die
White-Noise-Zufallsvariable Ut hervorgerufen werden. Sie haben eine konstante Varianz
Var(Yt) = Var(Ut) = 2 und sind unkorreliert: Cov(Yt, Yt-τ) = Cov(Ut, Ut-τ) = 0.
Eliminiert man den linearen Trend ßt, dann werden die Zeitreihenwerte näherungsweise
zufällig um einen konstanten Mittelwert  streuen.
Differenzstationärer Prozess
Y(t) Differenzstationärer Prozess: Y(t) = 0.2 + Y(t-1) + U(t)
35
(Ut):White-Noise-Prozess
mit E(Ut) = 0 und Var(Ut) = 3
30
25
20
15
10
5
0
10
20
30
40
50
60
70
80
90
100 t
Differenzstationärer Prozess (4.5):
Erwartungswert: E(Yt )      t
Stochastische Trends, die durch Kumulation der White-Noise-Zufallsvariablen Ut erzeugt
werden. Yt hat eine zeitvariable Varianz und weist eine von 0 verschiedene Kovarianz auf.
Durch Differenzenbildung kann die Zeitreihe in eine Reihe überführt werden, die näherungsweise zufällig um einen konstanten Mittelwert  streuen.
Substituieren wir nun in (4.5) Yt-1 durch
Yt 1    Yt 2  Ut 1
dann erhalten wir
Yt  2  Yt 2  Ut  Ut 1
Substitution von Yt-2 durch
Yt 2    Yt 3  Ut 2
führt zu
Yt  3  Yt 3  Ut  Ut 1  Ut 2
Nach sukzessiver Substitution erhält man die Beziehung
t -1
(4.6) Yt    t   U t - τ
τ 0
wenn man der Einfachheit halber einen Startwert y0=0 annimmt.
Prozessvarianz: Var (Y )  t  2
t
Autokorrelationskoeffizient:  t ,s 
t
, ts
s
Fall 1:
Langfristig wachsende Zeitreihe (yt)
Um zwischen einem Random Walk mit Drift und einem trendstationären Prozess zu
differenzieren, geht der Dickey-Fuller-Test (DF-Test) von der Schätzgleichung
(4.7) Yt  (  1)Yt 1    ß  t  Ut
aus, die sich aus einer Verknüpfung der Trendgleichung (4.4) und (4.5) ergibt. Die beiden
Konstanten  und  sind dabei durch die einheitliche Konstante µ ersetzt worden. Für =1
und ß=0 geht Gleichung (4.7) in einem Random Walk mit Drift über, während man für=0
und ß≠0 einen trendstationären Prozess erhält. Ein Random Walk mit Drift bei einem
gleichzeitig vorhandenem determininistischen Zeittrend wird in der Ökonomie als
unrealistisch ausgeschlossen.
Wenn die Zeitreihe (yt) aber trendbehaftet ist und das gleichzeitige Eintreten eines deterministischen und stochastischen Trends ausgeschlossen werden kann, lässt sich statt eines
simultanen Tests der Regressionskoeffizienten –1 und ß (auf Basis der F-Statistik) ein
einfacher Test (auf Basis der t-Statistik) durchgeführen. Der Dickey-Fuller-Test (DF-Test)
stellt die Nullhypothese
H0: –1=0, d.h. =1 (Random Walk mit Drift)
der Alternativhypothese
H1: –1<0, d.h. <1 (Trendstationarität)
gegenüber. Da >1 einen explosiven Prozess hervorrufen würde, ist der DF-Test ein
einseitiger Test.
Die Prüfgröße des DF-Tests,
(4.8)
t
ˆ  1
ˆ ˆ
folgt unter der Nullhypothese der Nichtstationarität allerdings nicht der t-Verteilung. Die
übliche Standardverteilung der t-Statistik (4.8) gilt nur unter der Annahme der Stationarität,
die hier nicht gegeben ist. Dickey und Fuller (1979) haben die Verteilung der Prüfgröße (4.8)
unter der Annahme der Nichtstationarität durch Simulation hergeleitet. Hierbei hat sich gezeigt, dass die Dickey-Fuller-Verteilung linksseitig der t-Verteilung liegt und stärker um
einen negativen Erwartungswert konzentriert ist. Abb. 4.1 stellt die Dickey-Fuller-Verteilung
der t-Verteilung für n=100 gegenüber.
Abb. 4.1: Dickey-Fuller-Verteilung und t-Verteilung (n=100)
f(t)
Dickey-Fuller-Verteilung
0,7
t-Verteilung
0,6
0,5
0,4
0,3
0,2
0,1
t
0
-6
-5
-4
-3
-2
-1
0
1
2
3
Für große Stichproben beträgt der kritische Wert der t-Verteilung bei einem Signifikanzniveau
von 5% t∞; 0,05 = –1,65, während der kritische Wert der Dickey-Fuller-Verteilung in dem hier
betrachteten Fall –3,41 beträgt. Die Nullhypothese der Nichtstationarität wird daher bei
einem großen Stichprobenumfang bei einem Signifikanzniveau von 5% angenommen, wenn
die Prüfgröße (4.8) größer oder gleich dem kritischen Wert DFw∞; 0,05 von –3,41 ist,[1]
t ≥ DFw∞; 0,05 = –3,41 => H0 annehmen, d.h. Nichtstationarität (Random Walk mit Drift),
und ablehnt, wenn die Prüfgröße (4.8) den kritischen Wert DFw∞;
unterschreitet:
0,05
(Trend) von 3,41
t < DFw∞; 0,05 = –3,41 => H0 ablehnen, d.h. Trendstationarität (zufällige Schwankungen um
einen linearen Trend).
Voraussetzung für die Anwendung des DF-Tests ist die White-Noise-Eigenschaft der
Störgröße Ut. Sie kann mit Hilfe eines Korrelogramms der Residuen oder dem Ljung-Box-Test
überprüft werden. Allgemein könnte eine Systematik der Störgröße durch einen ARMAProzess modelliert werden. Beim DF-Test beschränkt man sich jedoch auf eine ARModellierung, d.h. man erweitert die Schätzgleichung (4.7) um zeitlich verzögerte
Differenzen ∆Yt-1, ∆Yt-2,..., ∆Yt-p in der y-Variablen. Man bezeichnet den auf der
Schätzgleichung
p
(4.9) Yt  (1  )Yt 1      t   Yt  j  U t
j1 für den Fall einer langfristig wachsenden
[1] Der Index w beim kritischen Wert steht
Zeitreihe.
basierenden Unit-Root-Test als Augmented Dickey-Fuller-Test (ADF-Test). Bei der Wahl
des maximalen Lags der differenzierten y-Variablen hat man sich grundsätzlich an einer Herstellung der White-Noise-Eigenschaft von Ut zu orientieren. Hierzu könnte ebenfalls wiederum
das Korrelogramm der Residuen in Verbindung mit dem Ljung-Box-Test herangezogen werden. Man könnte sich aber bei der Wahl von p auch an dem gerade noch signifikanten Lag
∆Yt-j orientieren. Da es sich als besser erwiesen hat, zu viele als zu wenige Lag-Terme einzubeziehen, erscheint der sich aus beiden Kriterien ergebende maximale Lag eine sich anbietende Strategie zu sein. In Ökonometrie-Programmen wie z.B. EViews lässt sich alternativ von
Informationskriterien wie z.B. AIC oder BIC Gebrauch machen.
Fall 2:
Langfristig nicht wachsende Zeitreihe (yt)
Wenn eine Zeitreihe (yt) langfristig nicht wächst, reduziert sich der hinter der Gleichung (4.4)
stehende Determinismus wegen ß=0 zu einer Konstanten, die jetzt mit μ bezeichnet wird und
die bei ökonomischen Variablen wie der Inflationsrate, der Arbeitslosenquote oder einem
Zinssatz typischerweise ungleich null wäre (μ≠0). In diesem Fall würde bei =0 Statio-narität
offenbar bedeuten, dass die Zeitreihenwerte zufällig um eine von null verschiedene Konstante
μ schwanken:
(4.10) Yt = μ + ut.
Entscheidend hierfür ist aber nicht, dass der autoregressive Parameter  gleich 0, sondern
kleiner als 1 (<1) ist. Denn in diesem Fall geht Gleichung (4.7) mit ß=0 nach Anwendung
des Erwartungswertoperators,
E(Yt) =   E(Yt-1) + μ + E(Ut), <1,
wegen E(Yt) = E(Yt-1) = μy und E(Ut) = 0 in die Form
(1-) μy = μ
und damit
(4.11)  y 

1 
über, so dass Yt ebenfalls um eine Konstante schwankt, die jetzt aber durch das Prozessmittel
(4.11) gegeben ist. Die Fluktuationen um den Prozessmittelwert enthalten hier eine AR(1)Systematik (allgemeiner: ARMA-Struktur möglich), die ein abdriften ausschließt.
Sofern die langfristig nicht-wachsende Zeitreihe (yt) dagegen nichtstationär ist, wird sie durch
den stochastischen Prozess
(4.12)
Yt = Yt-1 + Ut
erzeugt, der sich aus Gleichung (4.5) mit  = 0 (bei Prozesskombination µ) ergibt. Es handelt
sich hierbei um einen Random Walk ohne Drift, dessen Nichtstationarität wir bereits gezeigt
haben. Sie ergibt sich aus der nicht-konstanten Varianz des Prozesses, die für t →∞ über alle
Grenzen wächst.
Eine Verknüpfung des Random Walks ohne Drift [Gl. (4.12)] mit stationären Schwankungen
um das Prozessmittel (4.11) ergibt die Schätzgleichung
(4.13)
Yt = μ +   Yt-1 + Ut (allgemein, mit =1: Random Walk),
die in der Form
(4.13’)
∆Yt = μ + (-1) Yt-1 + Ut
dem DF-Test zugrunde liegt. Zu testen ist hier die Nullhypothese
H0:  – 1 = 0, d.h.  = 1 (Random Walk ohne Drift)
gegen die Alternativhypothese
H1:  – 1 < 0, d.h.  < 1 (Stationarität).
Wie im Fall 1 folgt die Prüfgröße:
t
(4.14)
ˆ  1
ˆ ˆ
einer Dickey-Fuller-Verteilung, die aber hier dichter bei der standardmäßigen t-Verteilung
liegt (Abb. 4.2). Der kritische Wert liegt in großen Stichproben z.B. bei einem Signifikanzniveau von 5% bei –2,86 und ist mithin größer als im Fall einer wachsenden Zeitreihe.
Abb. 2:
Dickey-Fuller-Verteilung und t-Verteilung (n=100)
f(t)
Dickey-Fuller-Verteilung
0,7
t-Verteilung
0,6
0,5
0,4
0,3
0,2
0,1
0
-6
-5
-4
-3
-2
-1
0
1
2
3
t
Da bei Annahme der Nullhypothese H0 :  = 1 eine Konstante μ ≠ 0 eine langfristig
wachsende Zeitreihe (yt) implizieren würde, was wir aber a priori ausgeschlossen haben,
können wir in diesem Fall auf Nichtstationarität in Form eines Random Walks ohne Drift
schließen: Bei Ablehnung der Nullhypothese gehen wir dagegen von einem stationärem
Prozess aus, der allgemein um einen konstanten Mittelwert μy schwankt. Speziell für  = 0
ergeben sich zufällige Schwankungen der Zeitreihenwerte um den Parameter μ.
Bei großen Stichproben lassen sich die Testentscheidungen z.B. bei einem Signifikanzniveau
von 5% wie folgt formalisieren:[1]
t≥ DFw,o,o5 =-2,86 => H0 annehmen, d.h. Nichtstationarität (Random Walk ohne Drift)
w
t< DF,o,o5 =-2,86 => H0 ablehnen, d.h. Stationarität (zufällige Schwankung um Konstante).
[1] Der Index beim kritischen Wert steht für den Fall einer langfristigen nicht wachsenden
Zeitreihe.
Beispiel: Stochastischer Prozess (Yt) mit reversiblen Abweichungen von y
Stochastischer Prozess: Yt = 0,1 + 0,8Yt-1 + Ut [AR(1)-Prozess]
(Ut): White-Noise-Prozess mit E(Ut) = 0 und Var(Ut) = 1
Stochastischer Prozess mit reversiblen Abweichungen
Y(t) vom Prozessmittelwert:Y(t) = 0,1 + 0,8*Y(t-1) + U(t)
5
4
3
2
1
0
-1
-2
-3
10
20
30
40
50
60
70
80
90
100 t
Beispiel: Stochastischer Prozess (Yt) mit nicht-reversiblen Abweichungen von y
Stochastischer Prozess: Yt = 0,1 + Yt-1 + Ut [AR(1)-Prozess]
(Ut): White-Noise-Prozess mit E(Ut) = 0 und Var(Ut) = 1
Stochastischer Prozess mit nicht-reversiblen Abweichungen
vom Prozessmittelwert:Y(t) = 0.1 + Y(t-1) + U(t)
Y(t)
24
20
16
12
8
4
0
10
20
30
40
50
60
70
80
90
100 t