„Körper kennen lernen“ Station 1

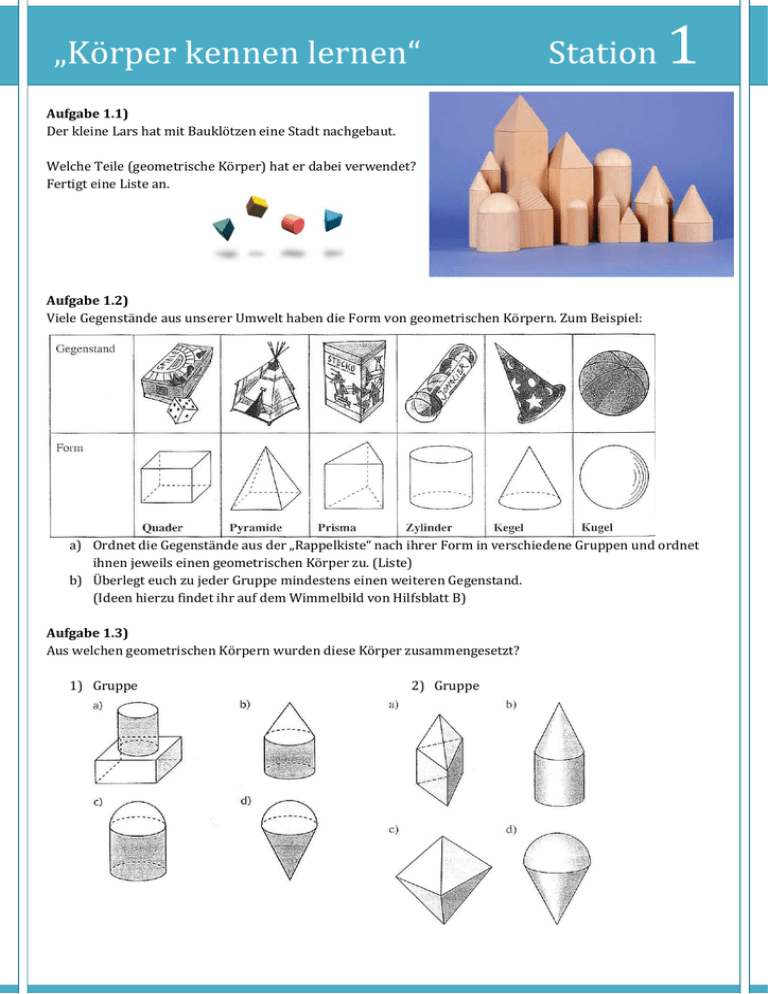
„Körper kennen lernen“
Station
1
Aufgabe 1.1)
Der kleine Lars hat mit Bauklötzen eine Stadt nachgebaut.
Welche Teile (geometrische Körper) hat er dabei verwendet?
Fertigt eine Liste an.
Aufgabe 1.2)
Viele Gegenstände aus unserer Umwelt haben die Form von geometrischen Körpern. Zum Beispiel:
a) Ordnet die Gegenstände aus der „Rappelkiste“ nach ihrer Form in verschiedene Gruppen und ordnet
ihnen jeweils einen geometrischen Körper zu. (Liste)
b) Überlegt euch zu jeder Gruppe mindestens einen weiteren Gegenstand.
(Ideen hierzu findet ihr auf dem Wimmelbild von Hilfsblatt B)
Aufgabe 1.3)
Aus welchen geometrischen Körpern wurden diese Körper zusammengesetzt?
1) Gruppe
2) Gruppe
Merkblatt zu
Stat
Station
1
Geometrische Körper
Bezeichnu
Bezeichnungen:
Geometrische Körper werden von Flächen begrenzt.
Geometri
grenzt. Beim Zylinder, beim
Kegel und bei der Kugel sind diese zum Teil auch
uch gewöl
gewölbt.
Die Seitenflächen
Seiten
zusammen bilden den Mantel,
alle Flächen
Fläch zusammen die Oberfläche des Körpers.
örpers.
Aneinander stoßende Flächen bilden eine Kante.. Beim Kegel gibt es zum
Aneinand
Beispiel auch
a
eine gebogene Kante, nämlich einen
inen Kreis
Kreis.
neinander stoßende Kanten bilden eine Ecke.
Aneinand
Folgend
lgende Körper werden nach der Form ihrer Grun
Grundfläche benannt:
Pyramiden
(Bsp.: Dreieckspyramide, quadratische Pyramide
amide, Achteckpyramide…)
Prismen
(Bsp.: Dreiecksprisma, Sechseckprisma…)
Hilfsblatt zu
Wimmelbild
Station
1
„Körper beschreiben“
Station
Aufgabe 2.1)
Beschreibe die Form der Flächen
a) eines Quaders,
b) einer quadratischen Pyramide,
c) eines Dreieckprismas.
Aufgabe 2.2)
„Schlafmütze – Spiel“
Aufgabe 2.3)
Welche Körper…
a) …bestehen nur aus quadratischen Flächen?
b) …besitzen eine Spitze?
c) …haben runde Deckflächen?
d) …bestehen aus einer Mantelfläche, die nur aus gleichen Dreiecken besteht?
e) …können verschiedene Vielecke als Grundfläche haben?
f) …besitzen zwei Kreisflächen?
g) …besitzen keine Ecken?
Aufgabe 2.4)
Nenne einen Körper mit:
a)
b)
c)
d)
e)
f)
5 Flächen, 8 Kanten und 5 Ecken
4 Flächen, 6 Kanten und 4 Ecken
5 Dreiecken und 1 Fünfeck als Fläche
nur gewölbten Kanten
keiner einzigen Kante
keiner einzigen Ecke
g)
h)
i)
j)
k)
l)
nur einer Fläche
nur einer Kante
mit Kanten, aber ohne Ecken.
Mit einer Kante und einer Ecke
12 gleich langen Kanten und 8 Ecken
9 gleich langen Kanten und 6 Ecken
Gibt es für manche „Steckbriefe“ mehrere Möglichkeiten?
2
„Körper beschreiben“
Aufgabe 2.5)
a) Welcher Körper ist hier gesucht?
Gesucht
ist der Körper mit:
- 5 Ecken
- 8 Kanten
- 4 Dreiecksflächen
- 1 quadratischen
Grundfläche
Aufgabe 2.6)
Station
b) Überlegt euch selbst weitere „Steckbriefe“ und
stellt sie einander als Rätsel.
(Hinweis: Schöne Exemplare werden im
Klassenzimmer aufgehängt ☺)
2
Merkblatt zu
Station
Körper werden nach ihren Eigenschaften eingeteilt:
Gerades und schiefes Prisma
2
„Kantenmodelle“
Station
3
Aufgabe 3.1)
Aus Trinkhälmen und Knetkügelchen kann man Kantenmodelle
herstellen, wie man sie auf dem Photo rechts sieht.
a) Für welche Körper ist das möglich, für welche nicht?
b) Bastelt zu jedem Körper, zu dem es möglich ist, ein
Kantenmodell. Wählt dabei eure Maße selbst.
c) Zusatzfrage:
Aus einem 18cm langen Trinkhalm soll das Kantenmodell
Eines Tetraeders hergestellt werden. Wie lang wird jede Kante?
Aufgabe 3.2) Krabbelkäfer
a) Ein Käfer sitzt auf der vorderen Ecke 1 des Kantenmodells eines Würfels und
möchte zur Ecke 7 krabbeln. Dabei soll aber keine Kante mehrmals durchlaufen
werden. Notiere 5 verschiedene Wege.
Wie lang ist der kürzeste, wie lang ist der längste Weg?
b) Nun will der Käfer jede Ecke des Würfels erkrabbeln. Auch dabei will er keine
Kante zweimal durchlaufen? Ist das möglich?
Aufgabe 3.3)
Lauras Vater ist Installateur. Er will für die Schule ein anschauliches Kantenmodell eines Würfels aus festen
Drahtstücken zusammenschweißen. Der Würfel soll eine Seitenlänge von 24 cm haben.
a) Wie viel cm Draht benötigt er dafür?
b) Wie viel Draht braucht er mehr, wenn die Kantenlänge 6 cm länger sein soll?
Aufgabe 3.4)
Aus insgesamt 96 cm Draht soll ein Kantenmodell
a) eines Würfels
b) einer quadratischen Pyramide hergestellt werden.
In welche Stücke muss der Draht jeweils geschnitten werden, wenn kein Reststück übrig bleiben soll?
Gibt es mehrere Möglichkeiten?
„Schrägbilder“
Station
4
Im täglichen Leben begegnen uns oft Abbildungen von Körpern, die einen räumlichen Eindruck vermitteln. Man
nennt solche Abbildungen Schrägbilder. Aber wie zeichnet man solche Bilder?
Mit dem Geobrett könnt ihr einfach Schrägbilder von Körpern herstellen.
Aufgabe 4.1)
Schrägbilder mit dem Geobrett
a) Spannt zunächst die unten gezeigten Schrägbilder mit den Gummis auf dem Geobrett nach.
b) Verändert die Schrägbilder der Quader im rechten Bild, indem ihr die Kantenlängen der Quader
vergrößert oder verkleinert.
c) Versucht danach eigene Schrägbilder von Körpern mit dem Geobrett darzustellen.
Aufgabe 4.2)
Zeichnen von Schrägbildern
Lernt das Zeichnen von Schrägbildern, indem ihr folgende Schritte auf einem karierten Blatt nachvollzieht:
„Schrägbilder“
Stat
Station
Aufgabe 4.3)
Ordnet den unten aufgeführten Kantenlän
Kantenlängen von Quadern das entsprechende Schrägbild
Schrägbi zu.
(2 Kästchen = 1 cm):
a)
b)
d)
1.Kantenlängen:
2.Kantenlängen:
3.Kantenlängen:
4.Kantenlängen:
5.Kantenlängen:
c)
e)
5 cm; 5 cm
cm; 1 cm
2 cm; 2 cm
cm; 2 cm
5 cm; 1 cm
cm; 1 cm
5 cm; 10 ccm; 1 cm
2 cm; 4 cm; 2 cm
6.Kantenlängen: 1,5 cm;; 1,5 cm; 3 cm
7.Kantenlängen: 3 cm; 1,5 cm; 2 ccm
8.Kantenlängen: 4 cm; 2 cm; 2 cm
9.Kantenlängen: 3 cm; 1,5 cm; 4 ccm
10. Kantenlängen: 2,5 cm;
m; 2 cm; 1
1,4 cm
Aufgabe 4.4)
ägbild einer
eine Siegertreppe für Sportler.
Aufgabe 4.5) Zeichne das Schrägbild
4
„Körpernetze“
Station
5
Aufgabe 5.1)
a) Welche der gezeichneten Netze lassen sich zu Würfeln zusammensetzen?
Probiert es mit den Klickies aus.
(Vielleicht könnt ihr bei einigen Netzen ohne Ausprobieren sagen, ob sich damit ein Würfel herstellen lässt,
oder nicht. Mit den Klickies lässt sich eure Vermutung dann ganz schnell überprüfen.)
b) Findet ihr weitere Würfelnetze?
c) Wie viele gibt es insgesamt?
Aufgabe 5.2)
Baue folgende Netze. Überprüfe jeweils, ob sich der gewünschte Körper aus deinem Netz bilden lässt.
a)
b)
c)
d)
e)
Das Netz einer Dreieckspyramide, die aus 16 Dreiecken besteht.
Das Netz für ein Dreieckiges Prisma.
Das Netz für einen Quader, der wie eine lange Schachtel aussieht.
Das Netz für eine Pyramide mit einem Fünfeck als Grundfläche.
Denke dir selbst einen Körper aus, für den du das Netz herstellst.
Zeichne alle Netze in deinen Ordner.
„Körpernetze“
Station
5
Tipp für die nächsten Aufgaben:
Nehmt euch 6 Quadrate in verschiedenen Farben und ordnet jeder Farbe einen Buchstaben, ein Symbol oder
eine Zahl zu. So könnt ihr die vorgegebenen Würfelnetze nachlegen und eure Vermutung überprüfen.
Aufgabe 5.3)
(Hinweis: G=Grundfläche)
„Körpernetze“
Aufgabe 5.4)
Station
5
„Körpernetze“
Aufgabe 5.5)
(Hinweis: G=Grundfläche)
Station
5
„Körpernetze“
Station
5
Aufgabe 5.6)
Aufgabe 5.7)
Ordne jedem Bild das passende Netz zu. Schreibe die passenden Zahlen-Buchstaben-Paare in deinen Ordner.
„Platonische Körper“
Station
6
Die Menschen waren schon immer von der geometrischen Regelmäßigkeit und Schönheit mancher Körper
fasziniert. So fanden schon die alten Griechen heraus, dass es nur vier weitere Körper gibt, die eine so
vollkommene Regelmäßigkeit besitzen wie der Würfel. Man nennt sie Platonische Körper. Betrachte die
Modelle.
Frage: Was bedeutet „vollkommene Regelmäßigkeit“? Betrachte dazu die Flächen und Kanten. Was fällt auf?
Aufgabe 6.1) Zähle die Flächen der Körper. Nach der Anzahl der Flächen werden die Platonischen Körper
benannt:
Vierflächner oder Tetraeder
Sechsflächner oder Hexaeder
Achtflächner oder Oktaeder
Zwölfflächner oder Dodekaeder
Zwanzigflächner oder Ikosaeder
Welchen anderen Namen hat also ein Würfel? Stelle die passenden Schilder vor die Modelle.
Die Griechen sahen in den Platonischen Körpern die Grundelemente der Welt: Erde (Würfel), Feuer (Tetraeder),
Luft (Oktaeder), Wasser (Ikosaeder). Das Dodekaeder stand für die ganze Welt, den Kosmos.
Die nächste Aufgabe ist schwierig. Versucht sie in der ganzen Gruppe zu lösen. Wenn ihr gar nicht weiter
kommt, fragt zuerst einen Experten und dann den Lehrer. Die Aufgaben d) und e) sind für „Spezialisten“.
Aufgabe 6.2) Warum gibt es nicht mehr als fünf Platonische Körper? Das soll diese Aufgabe beweisen.
a) In einem n-Eck beträgt die Summe aller Winkel (n-2) ⋅ 180° (für n ≥ 2). Wie groß ist also die
Winkelsumme in einem Dreieck, Viereck, Fünfeck, Sechseck?
b) In einem regelmäßigen n-Eck sind alle Winkel gleich groß. Wie groß ist also ein Winkel im
regelmäßigen Dreieck, Viereck, Fünfeck, Sechseck?
c) Damit ein Körper entsteht, muss die Summe aller in einer Ecke zusammenstoßenden
Winkel kleiner als 360° sein. Warum?
d) Wie viele regelmäßige Dreiecke (Vierecke, Fünfecke, Sechsecke) können also in einer Ecke
eines Körpers zusammenstoßen? Suche alle Möglichkeiten und begründe, warum es nicht
mehr geben kann.
e) Warum gibt es also genau fünf Platonische Körper?
regelmäßiges Dreieck,
Viereck, Sechseck:
„Eulersche Polyederformel“
Station
7
(nach Leonhard Euler, 1707 – 1783)
Definition:
Ein Körper, der nur von ebenen Flächen begrenzt wird, heißt Vielflächner oder Polyeder.
Frage:
Welche geometrischen Körper sind keine Polyeder?
Aufgabe 7.1) Ein Polyeder besitzt Flächen, Kanten und Ecken. Betrachte die Körpermodelle und fülle folgende
Tabelle aus, die an der Station ausliegt.
Zeile
Körper
1
Quader
2
Würfel
3
Prisma
4
Dreieckspyramide
(Tetraeder)
5
Viereckspyramide
Anzahl e
der Ecken
Anzahl f
der Flächen
e+f
Anzahl k der
Kanten
Welcher Zusammenhang besteht zwischen e, f und k?
Das ist die Eulersche Polyederformel. Ergänze sie im folgendem Kasten.
Eulersche Polyederformel:
In einem Polyeder gilt:
Aufgabe 7.2) Diese Aufgabe ist nur für Schüler, die bereits „Station 6 – Platonische Körper“ bearbeitet haben.
Gilt auch hier die Polyederformel?
6
Oktaeder
7
Dodekaeder
8
Ikosaeder
Aufgabe 7.3) Gilt auch bei dem ausgelegten Körper die Polyederformel?
„Eulersche Polyederformel“
Station
7
Aufgabe 7.3) Der Körper in nebenstehender Abbildung ist aus
Dreiecken und Quadraten zusammengesetzt.
a) Wie viele Dreiecke und wie viele Quadrate sind es?
b) Bestimme e, f und k und überprüfe die Eulersche
Polyederformel. Zähle geschickt!
Aufgabe 7.4)
Fußbälle sind meistens aus Fünfecken und Sechsecken
zusammengesetzt.
Überprüfe die Eulersche Polyederformel an einem
Fußball. Zähle auch hier geschickt!
„Symmetrie“
Stat
Station
8
rper sind eebenensymmetrisch? Wie viele Symmetrieebe
metrieebenen haben sie?
Aufgabe 8.1) a) Welche der Körper
b) Nenne 2 Gegenstände
nstände (Objekte)
(O
aus dem täglichen Leben, diee drehsym
drehsymmetrisch sind.
Aufgabe 8.2) Nutze die Bauklötze
tze und di
die Kartonbögen auf dem Arbeitstisch:
Aufgabe 8.3) Bestimme alle Symmetriee
mmetrieebenen
a) eines Quaders.. Nutze dazu
da wieder die Bauklötze und die Kartonbögen
tonbögen auf dem Arbeitstisch.
b) eines Würfels.. Probiere es an einem Kantenmodell eines Würfels
rfels oder an Bauklötzen aus.
Wie viele Symmetrieebene
trieebenen gibt es jeweils?
Aufgabe 8.4)
Gib jeweils den Symmetriepartner
ner an.
a)
b)
B ?
A ?
E ?
G ?
H ?
Aufgabe 8.5) Wie viele Symmetrieebenen
trieebenen hat eine Kugel?
Merkblatt zu
MERKE:
Man unterscheidet
ebenensymmetrische
Die Symmetrieebene E zerlegt den
Körper in 2 spiegelbildliche Hälften.
ften.
Stat
Station
und
drehsymmetrische Körper.
Bei Drehung um eine Drehachse
hse
kommt der Körper mit sich
ch selbst zur
z Deckung.
8
Anzahl/Körper Würfel Quader Dreieckspyramide quadrat. DreiecksPyramide Prisma
Ecken
8
Kanten
12
9
Kanten an
Boden 3
einer Ecke
Spitze 4
Kanten
4 / 4/
gleicher Länge
4
Anzahl/Körper Würfel Quader Dreieckspyramide quadrat. DreiecksPyramide Prisma
Ecken
8
Kanten
12
9
Kanten an
Boden 3
einer Ecke
Spitze 4
Kanten
4 / 4/
gleicher Länge
4
Anzahl/Körper Würfel Quader Dreieckspyramide quadrat. DreiecksPyramide Prisma
Ecken
8
Kanten
12
9
Kanten an
Boden 3
einer Ecke
Spitze 4
Kanten
4 / 4/
gleicher Länge
4
Anzahl/Körper Würfel Quader Dreieckspyramide quadrat. DreiecksPyramide Prisma
Ecken
8
Kanten
12
9
Kanten an
Boden 3
einer Ecke
Spitze 4
Kanten
4 / 4/
gleicher Länge
4
Anzahl/Körper Würfel Quader Dreieckspyramide quadrat. DreiecksPyramide Prisma
Ecken
8
Kanten
12
9
Kanten an
Boden 3
einer Ecke
Spitze 4
Kanten
4 / 4/
gleicher Länge
4