Handout zum Seminarvortrag Kernfusion

Handout zum Seminarvortrag Kernfusion
Christoph Rosner
1
Grundlagen
Unter Kernfusion verstehen wir die Verschmelzung zweier leichter Kerne zu einem schwereren. Die allgemeine
Reaktionsgleichung hierfür hat die folgende Form:
A+B →C +x+Q
(1)
Dabei sind:
• A, B, C: Kerne
• x: zusätzliches Reaktionsprodukt, z.b. Gammateilchen
• Q: Energie, die bei dem Prozess frei wird oder aufgewendet werden muss.
Ob die Reaktion exotherm oder endotherm ist, das Q also positiv oder negativ, hängt dabei von der
Bindungsenergie pro Nukleon der Ausgangskerne und der Endprodukte ab: ist die Summe der Massen der
Endkerne kleiner als die der Produkte, so wird die Massendifferenz nach ∆E = ∆mc2 als Energie frei. Ist die
Masse der Produkte grösser, muss diese Energie entsprechend aufgewendet werden, um die Reaktion
ablaufen zu lassen.
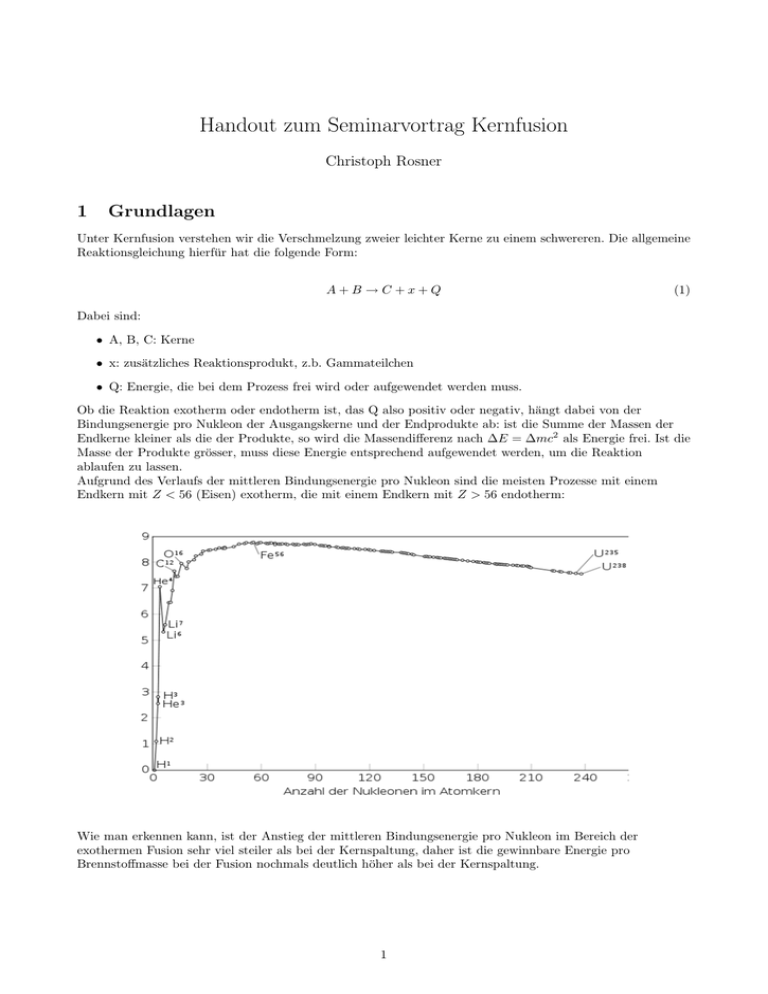
Aufgrund des Verlaufs der mittleren Bindungsenergie pro Nukleon sind die meisten Prozesse mit einem
Endkern mit Z < 56 (Eisen) exotherm, die mit einem Endkern mit Z > 56 endotherm:
Wie man erkennen kann, ist der Anstieg der mittleren Bindungsenergie pro Nukleon im Bereich der
exothermen Fusion sehr viel steiler als bei der Kernspaltung, daher ist die gewinnbare Energie pro
Brennstoffmasse bei der Fusion nochmals deutlich höher als bei der Kernspaltung.
1
Vor der Fusion müssen die beiden reagierenden
Kerne zunächst die abstossende Coulombbarriere
überwinden. Eine direkte Überwindung dieser Barriere würde bereits bei zwei Wasserstoffisotopen, deren Abstossung aufgrund von Z=1 am geringsten von
allen Kernen ist, eine sehr hohe Energie erfordern.
Aufgrund des Tunneleffekts ist es jedoch möglich,
dass auch Kerne mit geringerer kinetischer Energie
die Barriere überwinden und im Bereich des attraktiven Kernpotentials landen, sodass Fusion stattfinden kann. Dieser Effekt, zusammen mit der MaxwellBoltzmann Geschwindigkeitsverteilung, sorgt dafür,
dass Fusion allein durch die thermische Energie der
Teilchen in einem Plasma beispielsweise in der Sonne,
aber auch bei auf der Erde erreichbaren Temperaturen
(≈ 107 K in der Sonne, ≈ 108 K auf der Erde aufgrund
des niedrigeren erreichbaren Drucks) möglich wird.
2
Natürliche Fusion: Fusionsprozesse in Sternen
Das große Vorbild der Energieerzeugung durch Fusion sind die Sterne, unter anderem auch unsere Sonne. Je
nach Größe und Alter des Sterns liefern dabei unterschiedliche Fusionsprozesse den Hauptanteil der Energie,
bei Sternen wie unserer Sonne ist es hauptsächlich die Fusion von 4 Wasserstoffkernen (Protonen) zu einem
Helium Kern:
4 1H ⇒
2.1
4
He + 2νe + 2e+ + 26, 7M eV
Proton Proton Kette
Dieser Prozess kann über verschiedene Mechanismen ablaufen. Der Mechanismus, der in Sternen mit
vergleichsweise niedriger Kerntemperatur (> 3 · 106 K)
wie auch in unserer Sonne vorherscht ist die sogenannte Proton-Proton Kette. Wie der Name besagt reagieren hier zunächst zwei Protonen miteinander zu einem
Deuterium Kern, wobei ein Proton unter Aussendung
eines Elektron-Neutrinos und eines Positrons zu einem
Neutron wird. Der Wirkungsquerschnitt für diese Reaktion ist sehr gering, sie stellt daher auch den ’Flaschenhals’ der Kette dar und ist auf der Erde mit den
von uns erreichbaren Bedingungen kaum zur Energiegewinnung nutzbar. Aufgrund der enormen Menge an
Protonen findet sie in der Sonne aber in ausreichender
Menge statt.
Hat sich der Deuteriumkern erst einmal gebildet,
reagiert er sehr schnell mit einem weiteren Proton zu
einem Helium-3 Kern, der dann so lange durch die
Sonne wandert bis er auf einen weiteren, auf die gleiche
Weise gebildeten Helium-3 Kern trifft und mit diesem
unter Aussendung zweier Protonen zu Helium-4 reagiert. Neben diesem Prozess (Proton-Proton I) treten
parallel noch andere Reaktionsketten mit unterschiedlichen Zwischenprodukten auf (Proton-Proton II, III
und andere), die Startreaktion und der Endkern sind
jedoch immer gleich.
2
(2)
2.2
CNO-Zyklus
Der 2. Mechanismus ist der so genannte CNO oder
auch Bethe-Weizsäcker Zyklus. Die Nettoreaktion, die
bei diesem abläuft, ist die gleiche wie bei der ProtonProton Kette, sie wird allerdings durch im Kern des
Sterns vorkommendem Kohlenstoff (C-12) katalysiert.
Zusammenfassend lässt er sich so beschreiben, dass
der Kohlenstoffkern nacheinander durch Einfang von
Protonen zu Kernen mit höherem Z (N, O) reagiert,
wobei sich zwei mal ein Proton unter Aussendung von
Neutrino und Positron in ein Neutron umwandelt. Die
so hinzugewonnenen Nukleonen (2 Protonen, 2 Neutronen) spalten sich dann in Form eines Heliumkernes
wieder ab, wodurch der C-12 Kern wieder in seinem
Ausgangszustand vorliegt.
Der CNO Zyklus tritt ab einer Kerntemperatur
von ca. 1, 3 · 107 K als Konkurrenzprozess zur ProtonProton Kette auf und ist ab ca. 1.7 · 107 K der vorherschende Mechanismus. Möglich sind auch ähnliche
Zyklen mit höheren Elementen (z.b. Fluor), die jedoch
nach dem gleichen Mechanismus ablaufen.
3
3
Technische Anwendung
3.1
Der Brennstoff
Bei der technischen Realisierung von Fusionsenergie können wir, wie bereits erwähnt, nicht einfach den
Mechanismus der Sonne kopieren, da für die dort ablaufenden Reaktionen die Wirkungsquerschnitte viel zu
klein sind, um einen Energiegewinn zu ermöglichen. Wir müssen uns daher nach anderen geeigneten
Reaktionen mit hohem Wirkungsquerschnitt und gleichzeitig hoher Energieausbeute umsehen. Die folgenden
Reaktionen sind eine Auswahl an geeigneten Kandidaten:
1. D + D → p + T + 4,03 MeV
2. D + D → n + 3 He + 3,27 MeV
3.
D + T → 4 He + n + 17,6 MeV
4. P + T → 4 He + γ + 19,8 MeV
5. D + 3 He → 4 He + p + 18,35 MeV
6. T + T → 4 He + 2n + 11,33 MeV
Am interessantesten ist für uns dabei die hervorgehobene 3. Reaktion. Diese hat eine vergleichsweise hohe
Energieausbeute und gleichzeitig bei den von uns erreichbaren Bedingungen den mit Abstand höchsten
Wirkungsquerschnitt, wie man im folgenden Diagramm im Vergleich mit den D-D Reaktionen sehen kann:
Ein Weiterer Vorteil der Reaktion ist die gute Verfügbarkeite der beiden Brennstoffe: Deuterium kommt zu
ca. 0,015% im natürlichen Wasser vor, steht also beinahe unbegrenzt zur Verfügung. Das Tritium kommt
dagegen kaum natürlich vor (≈ 20 kg auf der gesamten Erde), kann jedoch aus Lithium mithilfe der
folgenden Reaktionen erbrütet werden:
7
Li + n →
6
4
Li + n →
He + T + n − 2, 47 M eV
4
He + T + 4, 78 M eV
(3)
(4)
Lithium kommt in natürlichen Gesteinen in ausreichender Menge vor. Die Erbrütung des Tritiums würde in
der Praxis im sogenannten Blanket um das Reaktionsgefäß stattfinden, in dem Lithium mit den 14.1 MeV
Neutronen aus der Fusionsreaktion reagieren würde.
4
3.2
Das Lawson Kriterium
Um eine Fusionsreaktion zum Laufen zu bekommen, muss man zunächst die Bedingungen (Dichte n,
Temperatur T) erreichen, bei denen die Fusion mit genügend hohem Wirkungsquerschnitt σ ablaufen kann.
Man muss also zunächst Energie investieren, um den Brennstoff auf ca. 108 K aufzuheizen und gleichzeitig
einen hohen Druck aufrecht erhalten, der Brennstoff liegt bei diesen Temperaturen dann als Plasma vor. Um
nun mehr Energie aus der Fusion herauszubekommen, als man hineingesteckt hat, muss dieses Plasma für
eine ausreichend lange Zeit τ (Einschlusszeit) zusammengehalten werden, sodass genug Fusionsreaktionen
ablaufen können um die aufgewandte Energie wieder reinzubekommen und zusätzliche, nutzbare Energie zu
produzieren. Die minimale Einschlusszeit (genauer das Produkt aus Einschlusszeit und Dichte), die hierfür
nötig ist, wird durch das sogenannte Lawson Kriterium ausgedrückt. Dieses kann man folgendermaßen
herleiten:
Die Energie, die pro Volumen durch die Fusionsreaktionen freiwird, ist gegeben durch
Ef = nd · nT · vσ · Q · τ =
1 2
n · vσ ·Q · τ
|4 {z }
(5)
Reaktionsrate
Dem gegenüber steht die Energie, die nötig ist um die Teilchen in diesem Volumen auf Zündtemperatur zu
bringen:
Eth = 3n · kb · T
(6)
Zur Energiegewinnung muss jetzt die aus der Fusion gewonnene Energie größer sein als die aufgewandte
Energie:
Ef =
1 2
n · vσ · Q · τ > 3n · kb · T = Eth
4
12kb T
⇒n·τ >
vσQ
(7)
(8)
Gleichung (8) stellt die einfachste Form des Lawson-Kriteriums dar.Berücksichtigt man zusätzlich die
Energieverluste durch Bremsstrahlung, die von den ständig durch Stöße beschleunigten geladenen Teilchen
des Plasma ausgesandt wird, sowie die Wirkungsquerschnitte η der Heizung und der Turbinen, die den
elektrischen Strom erzeugen, kommt man auf eine etwas kompliziertere Formel:
n·τ >
3kb T
η
1
4 vσQ 1−η
1
−
(9)
bT 2
|{z}
Bremsstrahlungsverluste
b ist hierbei ein konstanter Faktor. Das Lawson Kriterium für die bereits besprochene D-T Reaktion liegt bei
ca. nτ > 1020 s/m3 , das für die D-D Reaktion bei ca. nτ > 1022 s/m3 . Wie man sieht, ist es für die D-T
Reaktion etwa um den Faktor 100 kleiner, was die Eignung dieser Reaktion nochmal bestätigt.
3.3
Reaktorkonzepte
Um das Lawson Kriterium zu erfüllen, gibt es nun verschiedene Ansätze:
• Hohe Dichte (≈ 1000 g/cm3 =
ˆ 1030 Teilchen/m3 ) und geringe Einschlusszeiten (≈ 10−9 10−10 s):
Trägheitsfusion
• Hohe Einschlusszeit τ (einige Sekunden) und geringe Dichten (≈ 1020 Teilchen/cm3):
Fusion durch magnetischen Einschluss
3.3.1
Trägheitsfusion
Bei diesem Konzept wird der Einschluss des Plasmas lediglich durch die Trägheit der Partikel gewährleistet,
das Plasma hält also nur für sehr kurze Zeit zusammen und man benötigt eine hohe Brennstoffdichte, damit
dennoch genug Reaktionen ablaufen können.
5
Technisch wird dieses Konzept realisiert, indem ein gefrorenes Pellet aus D-T Brennstoff von allen Seiten
symmetrisch mit hochenergetischen Laser- oder Schwerionenstrahlen beschossen wird (1). Die äusserste
Schicht des Pellets geht dadurch explosionsartig in den Plasmazustand über, durch den dabei entstehenden
Rückstoß breiten sich Schockwellen in Richtung des Kerns des Pellets aus und verdichten dieses weiter (2).
Diese Schockwellen treffen dann im Kern des Pellets aufeinander, wodurch Druck und Temperatur so weit
steigen, dass die Fusion zünden kann (3). Durch die bei der Fusion entstehenden Alpha-Teilchen wird der
Rest des Pellets weiter erhitzt, sodass sich der Fusionsbereich ausbreiten kann. Es entsteht eine
Kettenreaktion, durch die im Idealfall ein Großteil des Brennstoffes reagiert (3).
Im Reaktorbetrieb müssten ähnlich wie bei einem Verbrennungsmotor mehrere hundert Pellets Pro Sekunde
zur Fusion gebracht werden, um ausreichend Energie zu erzeugen. Eines der grösten ungelösten Probleme bei
diesem Reaktor Konzept sind die hohen Anforderungen an die Laser (bzw. die Beschleuniger zur Erzeugung
der Ionen). Im Falle von Lasern wäre eine Pulsleistung von 5-10 MJ in ca 20 ns nötig, was einer Leistung von
500 TW entspricht (zum Vergleich: die gesamte Stromerzeugungsleistung der USA liegt im 2-stelligen TW
Bereich). Die stärksten heute verfügbaren Laser erreichen ca. 1 MJ bei dieser Pulsdauer. Bei der Verwendung
von Schwerionenstrahlung müsste man dagegen eine sehr hohe Stromstärke erreichen, um das Pellet schnell
genug aufzuheizen (≈ 106 A), heutige Beschleuniger erreichen diese Stromstärken bei weitem nicht.
Ein weiteres Problem liegt in den hohen Anforderungen an die Symmetrie der Implosion: treffen nicht alle
Strahlen das Pellet zur exakt selben Zeit im richtigen Winkel, treffen die Schockwellen nich ausreichend
genau im Kern des Pellets zusammen, um die Fusion zu zünden.
3.3.2
Fusion durch magnetischen Einschluss: Tokamak
Beim zweiten Ansatz versucht man, das Plasma für eine sehr viel längere Zeit unter
Zündbedingung zusammenzuhalten, wodurch sehr geringe Plasmadichten ausreichen
um das Lawson Kriterium zu erfüllen. Die Trägheit der Teilchen reicht nun nicht mehr
für den Einschluss aus, man muss diese aktiv einschliessen, beispielsweise durch ein geeignetes Magnetisches Feld. In einem solchen Feld beschreiben die geladenen Teilchen
des Plasmas Kreis- oder Spiralbahnen um die Feldlinien, sie können also nicht radial
zu diesen davonfliegen. Sind die Feldlinien zudem in sich gescchlossen, beispielsweise in
einer Ringförmigen Anordnung, können die Teilchen auch nicht entlang der Feldlinien
entkommen, sie sind also in dem Magnetischen Feld eingesperrt. Da bei einer solchen
ringförmigen Anordnung die Feldlinien nach aussen hin dünner werden, würden die
Teilchen radial nach aussen driften. Um das zu verhindern, muss man zusätzlich eine
Verdrillung der Feldlinien erreichen.
Abbildung 1: Magnetische Feldlinien
6
Beim einfachsten Konzept des magnetischen Einschlusses, dem sogenannten
Tokamak Reaktor, wird das primäre toroidale Feld durch eine ringförmige
Anordnung von Feldspulen erzeugt, während die Verdrillung der Feldlinien durch
die Überlagerung eines poloidalen Feldes, dessen Feldlinien kreisförmig um die des
primären Feldes verlaufen, erreicht wird. Um dieses poloidale Feld zu erzeugen, wird mit Hilfe eines
Transformators in der Mitte der Anordnung ein Strom im Plasma erzeugt, der dann von ringförmigen
magnetischen Feldlinien umgeben ist.
Der Vorteil dieses Prinzips ist seine sehr einfache Bauweise, durch die dennoch sehr gute Werte für das
Lawson Kriterium erreicht werden können. Der Hauptnachteil des Konzeptes ist jedoch der benötigte
Plasmastrom, der durch den Transformator nur gepulst erzeugt werden kann. Daher ist in dieser
Konfiguration kein Dauerbetrieb des Reaktors möglich, was für ein späteres Kraftwerk eine wichtige
Eigenschaft wäre.
Um dieses Problem zu lösen gibt es verschiedene Ansätze, für gewöhnlich wird versucht, den Stromtrieb auf
anderem Wege hinzubekommen (beispielsweise durch tangentiale Einstrahlung von elektromagnetischen
Wellen).
3.3.3
Fusion durch magnetischen Einschluss: Stellerator
Bei diesem Reaktortyp wird versucht, die Verdrillung der Feldlinien ohne einen Plasmastrom zu erreichen,
indem ein einzelnes Set von geeignet geformten Spulen verwendet wird. Diese Spulen haben dann natürlich
eine sehr komplizierte, nicht axial-symmetrische Form, deren Optimierung sehr leistungsfähige Rechner
erfordert. Daher ist dieser Reaktortyp auch erst seit kurzem konkurrenzfähig zu dem des Tokamak was die
Erreichung des Lawson Kriteriums angeht, auch wenn das Konzept schon relativ lange existiert.
7
4
Aktuelle Experimente und erreichte Parameter
Neben den drei vorgestellten Konzepten gibt es natürlich noch weitere, doch diese drei sind die
vielversprechendsten Kandidaten für ein zukünftiges Kraftwerk. Sie werden in verschiedenen aktuellen
Projekten erforscht, in denen versucht wird, die Probleme auf dem Weg zu einem funktionierenden
Fusionskraftwerk zu lösen (z.B. Heizmethoden für das Plasma, Entfernung von Verunreinigungen und
Heliumasche aus dem Plasma, Kontrolle von Plasmainstabilitäten, Nachfuhr von Brennstoff, Erbrütung des
Tritiums etc.). Am weitesten Vorangeschritten ist die Forschung bei den Tokamak Reaktoren, nach diesem
Prinzip soll auch das erste geplante Fusionskraftwerk DEMO (geplante Fertigstellung 2030) funktionieren.
Die erwähnenswertesten aktuellen Projekte zu den drei Konzepten sind:
1. Trägheitsfusion: NIF (National Ignition Facility)
• In Betrieb seit Januar 2010 in den USA
• Betreibt den stärksten Laser der Welt mit Pulsleistung von >1 MJ inerhalb von einigen ns
• Der Laser wird in 192 Teilstrahlen aufgeteilt und in einer Targetkammer auf das Brennstoffpellet
geschossen
• Die Anlage ist eigentlich zur Simulation von Kernwaffen gedacht, ’nebenbei’ wird aber auch die
Energiegewinnung durch Fusion erforscht
2. Stellerator Prinzip: Wendelstein 7-x
• Fertigstellung für 2014 geplant, Standort Greifswald in Deutschland
• Wird vom IPP (Institut für Plasmaphysik) in München betrieben und ist der Nachfolger des
Wendelstein 7-AS
• Soll die Kraftwerkstauglichkeit und die Möglichkeit zum Dauerbetrieb des Stelleratorkonzeptes
demonstrieren
3. Tokamak Prinzip: ITER (International Thermonuclear Experimental Reactor, Iter=lat. der Weg)
• Baubeginn 2009, Fertigstellung 2018 in Cadarache, Frankreich geplant
• Internationale Kollaboration von Japan, EU, Korea, China, Indien, Usa und Russland
• Veranschlagte Gesamtkosten des Projekts: 10 Milliarden Euro
• Soll erstmals einen positiven Energieverstärkungsfaktor von Q≈10 haben und somit die
Kraftwerkstauglichkeit des Tokamak Prinzips demonstrieren
Die bisher erreichten Fusionsparameter der verschiedenen Projekte sind in folgender Graphik zu sehen:
8
5
Quellen
Literatur:
• Musiol, Ranft, Reif: Kern und Elementarteilchenphysik
• Bethge, Walter Wiedeman: Kernphysik
Webseiten:
• http://www.ipp.mpg.de/ippcms/de
• http://www.iter.org/
• http://wikipedia.de/
• http://www.erkenntnishorizont.de/energie/kernfusion/fusionsprinzip.c.php
• https://lasers.llnl.gov
9