Massenmittelpunkt - homepage.ruhr-uni
Werbung
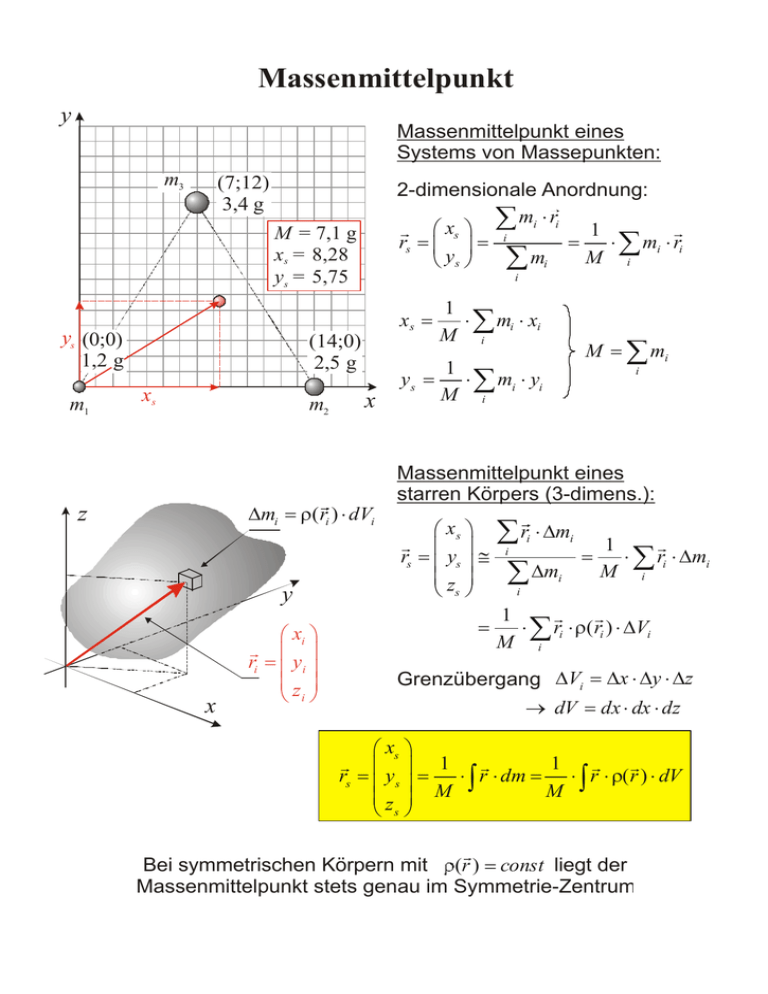
Massenmittelpunkt y Massenmittelpunkt eines Systems von Massepunkten: m3 (7;12) 3,4 g 2-dimensionale Anordnung: m ⋅r r xs i i i 1 r rs = = = ⋅ ∑ mi ⋅ ri ys ∑ mi M i M = 7,1 g xs = 8,28 ys = 5,75 xs = ys (0;0) 1,2 g m1 i (14;0) 2,5 g xs m2 x ∆mi = ρ( ri ) ⋅ dVi z y x xi r ri = yi z i ys = 1 ⋅ ∑ mi ⋅ xi M i M= 1 ⋅ ∑ mi ⋅ yi M i mi i Massenmittelpunkt eines starren Körpers (3-dimens.): xs r rs = ys ≅ z s = ∑ r ⋅ ∆m ∑ ∆m i i i i = 1 r ⋅ ∑ ri ⋅ ∆mi M i i 1 r r ⋅ ∑ ri ⋅ρ( ri ) ⋅ ∆Vi M i Grenzübergang ∆Vi = ∆x ⋅ ∆y ⋅ ∆z → dV = dx ⋅ dx ⋅ dz xs 1 1 r r r r rs = ys = ⋅ ∫ r ⋅ dm = ⋅ ∫ r ⋅ ρ( r ) ⋅ dV M z M s Bei symmetrischen Körpern mit (r ) const liegt der Massenmittelpunkt stets genau im Symmetrie-Zentrum Translationsbewegung starrer Körper MassenMittelpunkt MassenMittelpunkt F3 F3 F1 F2 F1 + F2 F1 + F2 F1 + F2 + F3 Bei einem starren Körper kann der Angriffspunkt einer Kraft entlang ihrer Richtung (”Wirklinie”) beliebig verschoben werden, ohne ihre Wirkung auf den Körper zu verändern Wenn die Resultierende der angreifenden Kräfte mit ihrer Wirklinie durch den Massenmittelpunkt verläuft, bewegt sich ein starrer Körper so, als ob seine gesamte Masse M im Massenmittelpunkt konzentriert sei: es tritt keine Drehung im Raum auf es gilt die Bewegungsgleichung Fres = Fi = M ⋅ a Drehbewegung starrer Körper MassenMittelpunkt (DrehAchse) Bei einem starren Körper führt eine angreifende Kraft nur dann zu einer Drehung, wenn die Wirklinie der Kraft nicht durch die Drehachse verläuft Ursache für ungleichförmige Drehbewegung (= Änderung der Winkelgeschwindigkeit): Drehmoment F h r sin r skalare Formel für den Fall, dass F und r in der Drehebene (d.h. senkrecht zur Drehachse) liegen: M F r sin F h vektorielle Formel unter Verwendung des Kreuzproduktes zweier Vektoren [allgemein: a × b = a ⋅ b ⋅ sin(Ra, b) ]: M =r ×F Anmerkung: Das Drehmoment als Ursache für eine Änderung der Winkelgeschwindigkeit übernimmt die Rolle der Kraft als Ursache für eine Änderung der linearen Geschwindigkeit Trägheitsmomente und Steiner’scher Satz Das Trägheitsmoment eines Körpers setzt sich additiv zusammen aus dem Trägheitsmoment IS bzgl. der Schwerpunktachse und dem Trägheitsmoment 2 m h der Gesamtmasse bzgl. der zur Schwerpunktachse parallelen Drehachse I = ∫ r 2 dm = ∫ ( x − a )2 + ( y − b) 2 dm ⇒ I = ∫ r 2dm = I S + m h 2 Kreisel r r r M = m rs × aG → M = m g ⋅ d r r dL = M dt dϕ r r L =I ⋅ω ωp = → dL = M ⋅ dt = L ⋅ d ϕ d ϕ M mg ⋅ d = = dt L I ⋅ω Winkelgeschwindigkeit der Präzession (weitere Informationen und Demonstrationen unter http://www.hcrs.at/GYRO.HTM ) Kreiselkompass Gegenüberstellung von Translation und Rotation Translation (feste Richtung) Rotation (feste Achse) Ort r r Winkelposition r θ Geschwindigkeit r r v = d r / dt Winkelgeschw. r r ω = d θ / dt Beschleunigung r r a = d v / dt Winkelbeschl. r r α = d ω / dt (träge) Masse m Trägheitsmoment I = ∫ r 2 dm Kraft 2. Newton-Axiom Arbeit r F r r Fges = m ⋅ a r r Fges = d p / dt r r dW = F ⋅ d r 1 Ekintrans = mv2 2 r Leistung (F = const) P = F ⋅ vr Kin. Energie Drehmoment r r r M =r ×F 2. Newton-Axiom r r M = I ⋅α r r M = dL / dt Arbeit r r dW = M ⋅ d θ Kin. Energie Leistung (M = const) 1 Ekinrot = I ω2 2 r r P = M ⋅ω linearer Impuls r r p = m⋅v r r pges = ∑ pi Drehimpuls r r r l=r× p r r r L = ∑ li = I ⋅ ω Erhaltungssatz r p ges = const Erhaltungssatz r L = const Rolle und Flaschenzug “feste” Rolle (Umlenkung ohne Kraftreduktion) VerteilungderGewichtskraft auf n “lose” Rollen: 1 Flr = ⋅ FG n “lose” Rolle (Halbierung der Gewichtskraft) Halbierungder Gewichtskraft aneiner “losen” Rolle 1 1 Fzug = ⋅ Flr = ⋅ FG 2 2n Bindungsenergie pro Nukleon (als Funktion der Massenzahl A) Kurve: Bethe-Weizsäcker-Formel (Tröpfchen-Modell) (Alonso-Finn: Quantenphysik und statistische Physik, S. 321) Folie 23 selbst-erhaltende Kettenreaktion: jeder Spaltprozess erzeugt im Mittel genau einen neuen Spaltprozess → Steuerungdes Neutronen-Haushalts wesentliche Komponenten eines Kern-Reaktors: 1) Brennstoff (z.B. 235U in ausreichender Menge) 2) Moderator (zum “Abbremsen” der schnellen Spaltungs-Neutronen) 3) Steuerstäbe (zur kontrollierten Absorption überzähliger Neutronen) z.B. 113 48 Cd + n → 114 48 Cd + γ oder 10 5 B + n → 73Li + α + γ 4) Kühlmittel (zur Wärme-Abfuhr) Folie41 Fusionsreaktionen sind die Energiequelle der Sonne und der Sterne. Bei einer Fusionsreaktion verschmelzen leichte Atomkerne zu massereicheren. Der Fusionsprozeß wandelt Masse (m) gemäß der Einstein-Formel E = mc2 in kinetische Energie (E) um. Eine Abfolge verschiedener Fusionsreaktionen, die sich “Proton-ProtonKette” nennt, erzeugt den größten Teil der Energie unserer Sonne und wird dies noch für einige Milliarden Jahre tun. Die p-p-Kette geht aus von Protonen, den Kernen des einfachen Wasserstoffatoms, und endet bei Alphateilchen, den Kernen des Heliumatoms. ENERGIEQUELLEN UND UMWANDLUNG Fusion Physik einer fundamentalen Energiequelle Um Fusion auf der Erde Wirklichkeit werden zu lassen, müssen Atome auf extrem hohe Temperaturen aufgeheiz werden, typisch auf mehr als 10 Millionen K. In diesem Zustand sind Atome ionisiert, sie bilden ein Plasma. Fü die Erzeugung nutzbarer Energie ist es notwendig, das Plasma lange genug zusammenzuhalten, d.h. e einzuschließen, damit genügend viele Verschmelzungsreaktionen stattfinden können. Wenn es gelingt Fusionskraftwerke zu bauen, hätten wir eine nahezu unerschöpfliche Energiequelle zur Verfügung. Die Brennstoff Deuterium und Lithium sind im Überfluß auf der Erde vorhanden. Wesentliche Fortschritte sind auf dem Weg z diesem Ziel bereits erreicht worden. PLASMA – DER VIERTE AGGREGATZUSTAND EIN ÜBERBLICK ÜBER ENERGIEUMWANDLUNGSPROZESSE EIGENSCHAFTEN TYPISCHER PLASMEN Energie kann viele verschiedene Formen annehmen und eine Vielzahl von Mechanismen kann eine Form in eine andere umwandeln. Während der Gesamtbetrag der Energie immer gleich bleibt, schränken die meisten Umwandlungsprozesse den tatsächlich nutzbaren Betrag spürbar ein. Plasmen bestehen aus frei beweglichen geladenen Teilchen, d.h. Elektronen und Ionen. Sie entstehen bei extrem hohen Temperaturen, wenn Elektronen vom bis dahin neutralen Atom abgetrennt werden. Sie sind in der Natur und im Universum allgegenwärtig. So bestehen Sterne z.B. vorwiegend aus Plasma. Man bezeichnet Plasmen als den vierten Aggregatzustand, weil sie einzigartige physikalische Eigenschaften aufweisen, die sie von Festkörpern, Flüssigkeiten und Gasen deutlich unterscheiden. Die Temperaturen und Dichten von Plasmen erstrecken sich über einen extrem weiten Parameterbereich. nutzbare Energie mechanisch elektrisch 10 Wärme VerlustEnergie Physikalische Parameter energiefreisetzender Reaktionen Reaktionstyp: chemisch Beispielreaktion C + O2 ⇒ CO2 1n + 235U ⇒143Ba +91Kr + 21n D (2H) + T (3H) ⇒ 4He+1n verwendeter Brennstoff Kohle,Öl und Luft UO2 (3% 235U + 97% 238U) Deuterium und Lithium 1000 1000 100 000 000 2,1 x 1012 3,4 x 1014 Typ. Temperatur (K) Kernspaltung Kernfusion ZWEI WICHTIGE FUSIONSPROZESSE pro kg Brennstoff freigesetzte E (J/kg) 3,3 x 107 D + T ⇒ 4He + 1n für die erste Generation von Fusionskraftwerken Brennstoffe WIE DIE FUSION FUNKTIONIERT D DIE KERNPHYSIK DER FUSION Fusion 20 keV Endprodukte 3,5 MeV p He 6 Li 4 2 0 16 O 3 He D 0 T 10 20 Kernmasse (u) nur Elemente geringer Masse Bindungsenergie pro Nukleon (MeV) Bindungsenergie pro Nukleon (MeV) 8 12 C T 10 62Ni Fusionsreaktionen setzen Energie frei 5 0 1 20 keV Energie von 1 eV entspricht einer Temperatur von 11 600 K. 50 100 150 Kernmasse (u) 200 Abgeleitet aus der Einstein-Formel ∆E = mc2. ∆E = pro Reaktion freigesetzte Energie; mi = Summe der Einzelmassen vor der Reaktion; mf = Summe der Massen der Reaktionsprodukte. In SI-Einheiten beträgt der Umrechnungsfaktor k=1; er beträgt 931,466 MeV/uc2, wenn E in MeV und m in atomaren Masseeinheiten (u) genommen wird. Teilchen Masse (u*) Neutron 1,008665 Proton 1,007276 Deuteron 2,013553 Triton 3,015500 Helium-3 3,014932 Helium-4 4,001506 * 1 u = 1,66054 x 10-27 kg = 931,466 MeV/c2 Ratenkoeffizient R (m 3/s) (Die Masse des Elektrons beträgt 0,000549 u.) Bezeichnung n (1n) p (1H) D (2H) T (3H) 3He α (4He) Ratenkoeffizienten von Fusionsreaktionen 10 –20 D+T 10 –24 10 –28 10 –46 10 –50 107 p+p Hauptmechanismus in der Sonne 108 109 1010 T ion (K) Reaktionsrate der Fusion = R n1n2 n1,n2 = Dichten der Reaktionspartner (Ionen/m3); R = Ratenkoeffizient (m3/s). Multipliziert mit ∆E erhält man die Leistungsdichte des Fusionsprozesses. γ 4He 3He p D ν e+ e- γ γ γ 6Be p SCHAFFUNG FUSIONSRELEVANTER BEDINGUNGEN PLASMAHEIZUNG UND -EINSCHLUSS Schwerkraft Magnetfelder Massenträgheit Für die Fusion werden Hochtemperaturplasmen benötigt, die hinreichend lange bei hoher Dichte eingeschlossen werden müssen, um Energie freizusetzen. Plasma eines entstehenden Sterns Tokamak Tokamak Laserfusion Laserfusion Typische Dimensionen: Heizmechanismen: <--------- Größe: 1019 m----------> Lebensdauer: 1015 - 1018 s Einschluß: <---------- Größe: 10 m ----------> Lebensdauer: 10-2 - 106 s • elektromagnetische Wellen • Kompression • Energie der Fusionsprodukte • ohm’sche Heizung (elektrischer Strom) • Neutralstrahl-Injektion (Wasserstoff-Atomstrahlen) • Kompression • Energie der Fusionsprodukte <------------ Größe:10-1 m ------------> Lebensdauer: 10-9 - 10-7 s • Kompression (durch Laser- oder Ionenstrahlen bzw. durch in Folge entstehende Röntgenstrahlen verursachte Implosion) • Energie der Fusionsprodukte Blitz Neon interstellarer Raum Polarlichter Fluoreszenzlicht Flammen 109 1015 Festkörper, Flüssigkeiten und Gase. Zu kalt und zu dicht für Plasmen. 1027 1033 1021 Dichte (Anzahl geladener Teilchen / m3) p p n 1 eV = 1,6022 x 10-19 J. Die mittlere kinetische Spaltungsreaktionen setzen Energie frei Nukleare Reaktionsenergie : ∆E = k (mi-mf) c2 Einige Kernmassen 14,1 MeV γ γ 3He p p Bindingsenergie pro Nukleon in Abhängigkeit der Kernmasse 4 ee+ 4He Die Verschmelzung von Elementen geringer Masse setzt genau wie die Spaltung von Elementen hoher Masse Energie frei. 10 ν D Sonneninneres Sonnenkorona Sonnenwind 102 103 “p-p”: DIE SOLARE FUSIONSKETTE p kosmische Nebel 106 104 Trägheitsfusion magnetische Fusion 8 Temperatur (K) Umwandlung nutzbare Eaus = η Eein η = thermodynamischer Wirkungsgrad; 10-40% sind typisch. AbfallMaterialien F U S I O N M Ö G L I C H M AC H E N EXPERIMENTELLE ERGEBNISSE DER FUSIONSFORSCHUNG Sowohl die Trägheitsfusion als auch die magnetische Fusion konzentrieren sich auf das Verständnis von Plasmaeinschluß und -heizung. Die Forschungsanstrengungen haben zu höheren Plasmatemperaturen Ti, Dichten ni und Energieeinschlußzeiten τ geführt. Zukünftige Fusionskraftwerke werden eine Leistung von typisch 1 GW liefern. Ihre Plasmen werden eine Temperatur von etwa Ti = 120 Millionen K haben, während der Einschlußparameter niτ etwa 2 x 1020 m-3 s betragen wird. Einschlußparameter n i τ (m-3s) Grundtyp chemisch, Schwerkraft, nuklear , solar, usw. 1021 reaktorrelevante Bedingungen 20 10 1019 1018 seit 1990 1980-90 1975-80 magnetisch 1970-75 1017 10 6 10 7 Trägheitsfusion 10 8 109 Ionentemperatur (K) Copyright © 1996 Contemporary Physics Education Project (CPEP). Translation by Forschungszentrum Jülich / TEC CPEP ist eine gemeinnützige Organisation von Lehrern, Dozenten und Physikern mit maßgeblicher Beteiligung von Studenten. Öffentlich und private Förderung sowie die Unterstützung durch Forschungsinstitute waren für dieses Projekt wesentlich und werden es auch Zukunft sein. Dieses Poster wurde von CPEP mit Hilfe der folgenden Organisationen entworfen: the AIP journal Physics of Plasmas, th Division of Plasma Physics of the APS, General Atomics, Lawrence Livermore National Laboratory, Massachusetts Institute of Technolog Princeton Plasma Physics Laboratory, the University of Rochester Laboratory for Laser Energetics, the U.S. Department of Energy und da Trilateral Euregio Cluster. Graphiken: NASA, the National Solar Observatory, Steve Albers und die oben genannten Organisationen.