Kernfusion - 99Documents

Dies ist nur ein Auszug!
Die komplette PDF gibt es hier.
Kernfusion
Physikalische Grundlagen
Bei der Kernfusion müssen 2 leichte Atomkerne miteinander verschmelzen, was
wegen der elektrostatischen Abstoßung zwischen beiden Kernen erschwert wird.
Damit die Kernfusion stattfinden kann, müssen sich die beiden Atomkerne sehr
nahe kommen. Erst wenn die Teilchen sich fast berühren, spüren sie die starke
Kernkraft, die sie zusammenhält und können die abstoßende elektrostatische
Kraft überwinden.
Die Coulombkraft
Gleich geladene Körper stoßen einander ab und ungleich geladene ziehen
einander an. Durch die stärkere Kernkraft ziehen sich die Nukleonen gegenseitig
an.
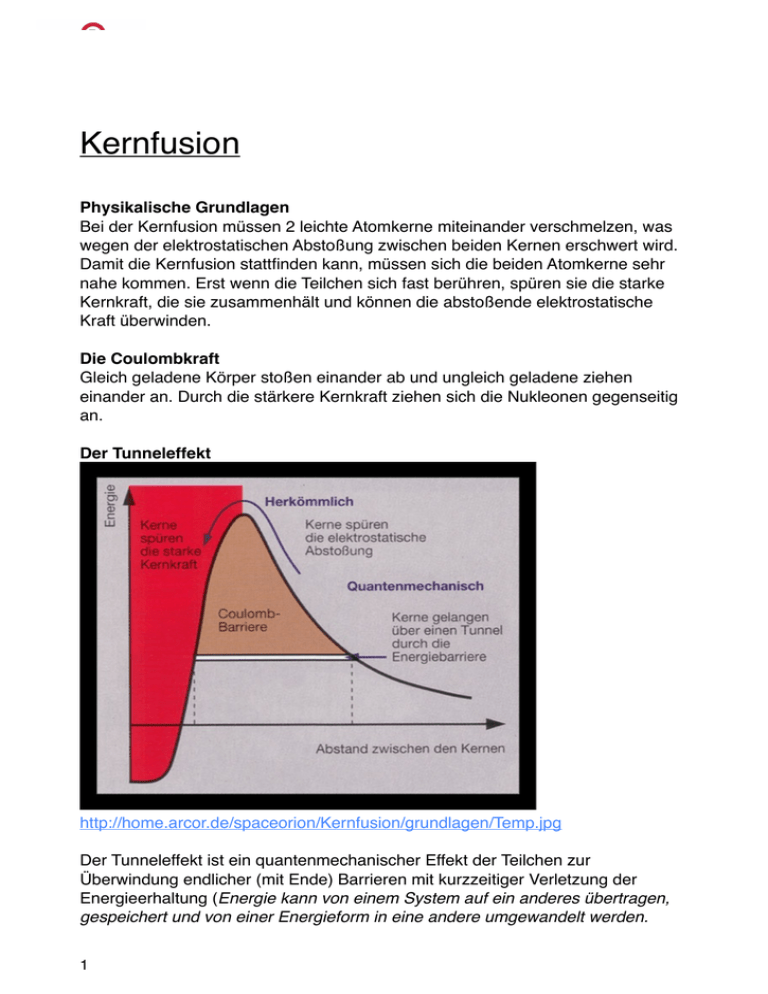
Der Tunneleffekt
http://home.arcor.de/spaceorion/Kernfusion/grundlagen/Temp.jpg
Der Tunneleffekt ist ein quantenmechanischer Effekt der Teilchen zur
Überwindung endlicher (mit Ende) Barrieren mit kurzzeitiger Verletzung der
Energieerhaltung (Energie kann von einem System auf ein anderes übertragen,
gespeichert und von einer Energieform in eine andere umgewandelt werden.
1
Dies ist nur ein Auszug!
Die komplette PDF gibt es hier.
Dabei ändert sich die Gesamtenergie nicht.) -> Teilchen leiht sich kurz Energie,
hüpft damit über einen Berg und gibt die Energie danach wieder zurück.
Es gilt, die Coulomb-Barriere zu erklimmen, denn um den Potentialwall/Gipfel zu
überwinden, bräuchte man Temperaturen von 2 Milliarden Grad, was technisch
unbeherrschbar wäre. Dank dem quantenmechanischen Tunneleffekt ist die
Fusion dennoch möglich. Die Teilchen tunneln durch den „Gipfel“ hindurch und
befinden sich plötzlich aufgrund der quantenmechanischen Ortsunschärfe auf der
anderen Seite, wo die Kerne die starke Kernkraft spüren. Die Wahrscheinlichkeit
für dieses Tunneln steigt mit zunehmender Geschwindigkeit des Teilchens, sowie
mit abnehmender Höhe und Breite des Potentialwalls. Die notwendige
Temperatur (Energie) reduziert sich damit auf 100 Mio. Grad. Gelangen die Kerne
in den Wirkungsbereich der starken Kernkraft (Wechselwirkung), findet die
Kernfusion statt. Bindungsenergie
Die Bindungsenergie ist die Energiemenge, die aufgewandt werden muss, um
den Atomkern in seine Nukleonen zu zerlegen. Umgekehrt wird eine ebenso
große Energie frei, wenn sich Nukleonen zu einem Kern vereinigen.
Prinzipiell können für die Kernfusion alle Atomkerne verwendet werden, aber die
Fusion (schwerer Kerne) ab dem Element Eisen ist energetisch negativ, also
muss Energie aufgewendet werden. Das heißt, ab Eisen nimmt die
Bindungsenergie je Nukleon wieder ab, denn je mehr Protonen vorhanden sind,
desto stärker ist die abstoßende Coulombkraft zwischen ihnen.
Massendefekt (-verlust)
Bei der Bildung von Atomkernen wird also Bindungsenergie abgegeben. Diese ist
auch nach E = ∆ mc^2 mit der Masse verknüpft. Daher ist die Masse eines
Atomkerns stets kleiner als die Summe seiner Bestandteile vor dem
Zusammenschluss. Der Massendefekt eines Kerns steigt mit der Massenzahl. Bei
Kernreaktionen geht die Massendifferenz ∆m in Energie über und wird in Form
von Strahlungs- oder kinetischer Energie freigesetzt. ∆m = E/c^2
Reaktionen
Für die Kernfusionsreaktionen sind leichte Atomkerne erforderlich. Hauptsächlich
werden Deuterium und Tritium, zwei Wasserstoffisotope, eingesetzt. ( = Je höher
die Ordnungszahl bzw. Protonenzahl, desto mehr Energie ist erforderlich ) Deuterium ist ein stabiles Wasserstoffisotop aus einen Proton und einem
Neutron. Seine Häufigkeit im Wasser liegt bei 1 Deuteriumatom pro 6.500
Wasserstoffatome. Das bedeutet, dass die Konzentration von Deuterium im
Meerwasser 34 Gramm/Kubikmeter beträgt. Der Energiegehalt von Deuterium ist
so groß, dass aus dem in einem Liter Meerwasser enthaltenen Deuterium, so viel
Energie gewonnen werden kann, wie aus 250 Litern Erdöl.
2
Dies ist nur ein Auszug!
Die komplette PDF gibt es hier.
Deshalb und weil drei Viertel der Erde mit Wasser bedeckt sind, wird die
Kernfusion als unerschöpfliche Energiequelle betrachtet.
Das andere bei der Kernfusion eingesetzte Element ist Tritium, ein instabiles und
radioaktives Wasserstoffisotop. Es besteht aus einem Proton und zwei Neutronen
und es zerfällt relativ schnell unter Emission von Betastrahlung. Tritium tritt in der
Natur nur selten auf, kann aber durch Neutroneneinfang aus Lithiumistopen
erzeugt werden. Lithium ist reichlich in der Erdkruste und im Meerwasser
vorhanden.
Beispielsreaktionen: D + T -> He + n + 17,6 MeV Bei der Fusion eines Deuteriumkerns mit einem Tritiumkern entstehen ein Helium
aus zwei Neutronen und zwei Protonen. Es werden 1 Neutron und 17,6 MeV
Energie freigesetzt.
4
D + D -> He + n + 3,2 MeV Bei der Fusion von zwei Deuteriumkernen entsteht ein Helium aus zwei Protonen
und einem Neutron. Es werden 1 Neutron und 3,2 MeV Energie freigesetzt.
3
D + D -> T + p + 4,03 MeV Bei der Fusion von zwei Deuteriumkernen entstehen ein Tritium, 1 Proton und
4,03 MeV Energie.
{ Einheit Megaelektronenvolt (MeV) }
Fusionsprodukt - Lawson-Kriterium
Damit ein Fusionsreaktor wirtschaftlich arbeiten kann, muss die durch Fusion
gewonnene Energie größer sein als die für die Plasmaheizung aufzuwendende
Energie. Ohne große Rechnung kann man einsehen, dass die Fusionsenergie mit
folgenden Parametern anwachsen wird.
Von Lawson stammt die folgende Abschätzung (Lawson Kriterium):
Das Fusionsprodukt gibt an, wie nahe man einem gezündeten Plasma
gekommen ist, in dem einzig die Heizung durch die per Fusion erzeugten
Helium-Kerne die Temperatur des Plasmas aufrecht erhält.
Das Fusionsprodukt setzt sich zusammen aus:
•
•
3
Plasmatemperatur T charakterisiert die kinetische Energie der
Plasmateilchen -> in der Nähe des Maximus des Wirkungsquerschnitts
Teilchendichte n (Teilchen pro m^3 ) trägt dazu bei, dass sich viele
Plasmateilchen möglichst nahe kommen -> höhere Stoßwahrscheinlichkeit