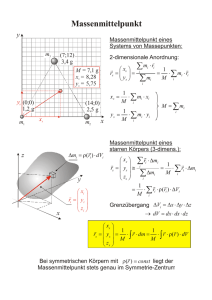
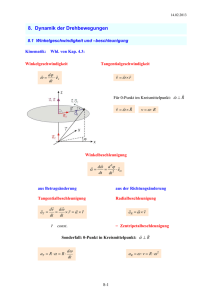
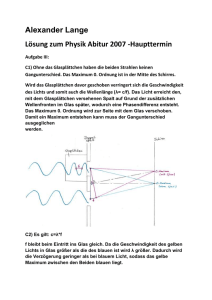
FF = −kx 1 2 kx2 1 2 mv2 1 2 mv2 + 1 2 kx2
Werbung

Beispiel: Feder Ohne Reibung bleibt bei einer Feder die mechanische Energie erhalten. FF = −kx € WF = -1/2 k (x22 – x12) = -(U(x2) – U(x1)) für x1=0 potentielle Energie: kinetische Energie: Wkin = U= 1 2 kx 2 1 2 mv€ 2 damit Gesamtenergie: € 1 1 E = Wkin + U = mv2 + kx2 2 2 € Graphische Darstellung: Abhängigkeit der kinetischen, potentiellen und Gesamtenergie als Funktion von der Auslenkung. 50 E U(x) Wkin(x) x U und Wkin sind Parabeln Wenn x = 0, dann hat die kinetische Energie ein Maximum und die potentielle Energie ist 0. E= 1 2 1 mv max = kA2 2 2 A ist die Amplitude oder Auslenkung € I.5.5 Satz von der Erhaltung der Energie (allgemein), konservative Kräfte Oben wurde die spezielle Form der Energieerhaltung studiert. Schwerkraft ist spezielle Kraft, sie gehört zu sogenannten konservativen Kräften. Die potentielle Energie lässt sich nicht für alle Kräfte einführen, sondern nur für konservative Kräfte. Definition: Eine Kraft heißt konservativ, wenn die von ihr zwischen den Punkten P1 und P2 geleistete Arbeit nicht von der Wahl des Weges abhängt. 51 P2 ∫ F • ds W= P1 ,Weg:I € oder wegen F ∫ • ds = F ∫ • ds P2 P2 P1 ,Weg:II P1 ,Weg:III = € F ∫ • ds = F ∫ • ds P2 P2 P1 ,Weg:I P1 ,Weg:II P1 ∫ F • ds + ∫ F • ds = 0 P2 € P1 P2 In Worten: € Bei einer konservativen Kraft verschwindet bei einer geschlossenen Wegführung die geleistete Arbeit: F ∫ • ds = 0 Versuch: € 52 Beispiel: Feder ∫ F • ds + z2 z1 z2 z1 ∫ F • ds z2 z1 = −k ∫ zdz - k ∫ zdz € z1 z2 k k = − (z22 − z12 ) − (z12 − z22 ) = 0 2 2 € Federkraft ist konservativ ⇒ € Wenn die Kraft F(s) konservativ ist, lässt sich die potentielle Energie finden: F ∫ • ds = U(P2 ) − U(P1) =: -ΔU P2 W= € P1 € € Für kleine Verschiebungen gilt: dW= F • ds = −dU dU = -Fxdx − Fy dy − Fzdz € eindim. Problem: € dy = dz = 0 € dU = -F x dx Durch Differenzieren von U(x) gewinnt man Fx. € 53 dreidim. Problem: dU = -Fxdx − Fy dy − Fzdz € € ∂U ∂U ∂U = -Fx , = -Fy , = -Fz ∂y ∂x ∂z € € Einführung des Vektoroperators grad F = -gradU = -∇U € ∂ ∂ ∂ ∇ = ex + ey + ez ∂x ∂y ∂z Ein Vektor wird erzeugt, wenn grad auf eine skalare Funktion € angewendet wird (z.B. U). Anschauliche Darstellung Orte gleicher potentieller Energie folgen aus U(x, y, z) = const. U(x,y,z) = const. ⇒ z = f(x,y) Gleichung einer Fläche € Diese Flächen heißen Äquipotentialflächen. 54 Beispiele: 1. Schwerefeld der Erde U=mgz U=0 für z=0 Fz = -(gradU)z = -(∇U) z − ∂U = -mg ∂z €Erdoberfläche € Linien U = const liegen parallel zur Erdoberfläche (Äquipotentiallinien). Kräfte stehen senkrecht zu Äquipotentiallinien. 2. Schwerefeld in Erdferne dU = - GmME dr r2 (neg. Vorzeichen bedeutet, dass man Arbeit anwenden muss, wenn man r vergrößern € will, dr > 0) r∞ U = -GmME ∫ r0 € dr 1 1 = −GmM ( − ) E r2 r0 r∞ U(r) = - € GmME r € 55 1 r∞ =: 0 Äquipotentiallinien sind konzentrische Kreise. Kräfte zeigen radial nach innen. Bild: Äquipotentiallinien 3. Fluchtgeschwindigkeit v0 EA = 1 GMEm mv20 − = E∞ = 0 2 RE r → ∞, v ∞ → 0 € € 1 GMEm mv20 = 2 RE mg = € GMEm R2E gR2E = GME 2gR2E € v = RE 2 0 € v0 = 2gRE g=9,81m/s2 RE=6,4x106m € € v0=11.2km/s 56 Allgemeine Formulierung des Energieerhaltungssatzes In einem abgeschlossenen System, in dem zwischen den Massen konservative Kräfte wirken, ist die Summe aus den kinetischen Energien der einzelnen Teilchen und den potentiellen Energien zwischen allen Teilchen konstant. Mechanischer Energiesatz: E = Wkin + U = cont. Nicht-konservative Kräfte F = F(v) € Durch etwaige Reibungskräfte nimmt kinetische Energie ab, die potentielle Energie wächst nicht im gleichen Maß. € Wkin + U = E nimmt mit der Zeit ab. Grund: Ein Teil der Energie wird in Energie der Bewegung der € Moleküle und in innere Energie der Moleküle umgewandelt. ⇒ Es gilt: z. B. Wärmeenergie Wkin + U + Enicht -mechanisch = const. Enicht-mechanisch = Wärmeenergie oder elektrische Energie €Versuch: Wärmeerzeugung 57 € € € I.6 Teilchensysteme Bis jetzt punktförmige Einzelmassen behandelt. Materie besteht aus vielen Einzelmassen, die untereinander wechselwirken. I.6.1 Impuls eines Teilchensystems Gesamtimpuls von n-Teilchen p = p1 + p2 + p3 ........ pn = n ∑p i i=1 Beispiel: zwei sich anziehende Massen 1) und 2) dp1 = F21 = F dt dp2 = F12 = −F21 = −F dt dp dp1 dp 2 = + =0 Daher: dt dt dt p = p1 + p2 = const. €Der Gesamtimpuls ist trotz Kraftwirkung der inneren Kräfte zeitlich konstant. €Verallgemeinertes 1. Newton’sches Gesetz: In einem abgeschlossenen Inertialsystem (d.h. es treten nur innere Kräfte auf) ist der Gesamtimpuls konstant (conservation of momentum). 58 Versuch: ausströmendes Wasser Videos: Video: Beispiel 1: Gewehr, Kanone -m1v1+m2v2=0 v2=(m1/m2)v1 Beispiel 2: Die Bewegung einer Rakete Die Masse der Rakete ist nicht konstant. Der Massenausstoß erzeugt Schubkraft. zur Zeit t: 59 zur Zeit t + dt: Impulserhaltung: Mv = (M − dm)(v + dv) + dm(−u + v + dv) = Mv + Mdv − dmv − dmdv − dmu + dmv + dmdv € Mdv = dmu € Nach dem Ausstoß wird die Masse der Rakete um dM = -dm € reduziert. Mdv = −dMu € € dv dM =− u M v(t B ) € Mleer (t =t B ) ∫ dv = −u v 0 =0,t =0 ∫ M0 ,t =0 dM M Sei v0 = 0 , dann gilt nach Brennschluss: € ⎛ M ⎞ v(t B ) = +uln⎜ 0 ⎟ ⎝ Mleer ⎠ Raketengleichung (rocket equation) € 60 Versuch: Rakete Video: Rocketman Jetzt: Zusätzlich äußere Kräfte: Verallgemeinertes 2. Newton’sches Gesetz: dp1 = F21 + Fäuß1 dt € dp 2 = F12 + Fäuß 2 dt € dp dp1 dp2 = + = Fäuß1 + Fäuß 2 = Fäuß dt dt dt € Auf n Massenpunkte verallgemeinern: Nur eine äußere Kraft kann den Impuls des Gesamtsystems ändern. Resultierende äußere Kraft = Summe der Einzelkräfte. Jetzt Raketengleichung mit Gravitationskraft: Fäuß = dp dv dm = M −u dt dt dt =M € 61 € dv dM +u dt dt dv dM M = Fäuß − u dt dt dv Mg dM =− −u dt M Mdt € v(t B ) € ∫ dv = −g v 0 =0,t =0 Mleer (t =t B ) ∫ dt − u t =0 ∫ M0 ,t =0 dM M ⎛ M ⎞ v(t B ) = -gt B + uln⎜ 0 ⎟ ⎝ Mleer ⎠ € Bilder: Beispiel: t =t B Daten der Rakete Saturn V € Daten der Rakete Saturn V M0 = 2.95 106 kg tB = 130 s u = 2.22 103 m/s Mleer = 106 kg ⎛ M ⎞ uln⎜ 0 ⎟ = 2401.6m / s ⎝ Mleer ⎠ v(tB) = -1275.3 + 2401.6 m/s € = 1126.3 m/s 62 v0 = 2gRE (Fluchtgeschwindigkeit) v0=11.2km/s € ⇒ ⇒ Mehrstufenrakete Strahlgeschwindigkeit hängt von der Temperatur in der Antriebsdüse ab. Daher WasserstoffSauerstoff als Treibstoff. I.6.2 Der Massenmittelpunkt und der Schwerpunktsatz In einem Inertialsystem ohne äußere Kräfte gilt: pM = p1 + p2 + ...+ pN = m1v1 + m2 v2 + ...+ mNvN Ein außen stehender Beobachter schreibt Massenpunkten € € die Masse M = m1 + m2 + ……+ mN PM = MvM und die Geschwindigkeit vM zu. vM heißt Geschwindigkeit des Massenmittelpunktes (centre of mass) und ist gegeben durch:€ € N mi vi ∑ P vM = M = i=1N M ∑mi € i=1 € 63 oder für den Ortsvektor: N rM = ∑m r ii i=1 N ∑m i i=1 Weiterhin gilt: dvM dPM N dvi N M = € = ∑mi = ∑Fäußi = Fäuß dt dt dt i=1 i=1 Schwerpunktsatz € Der Massenmittelpunkt eines beliebigen Systems materieller Punkte bewegt sich so als sei in ihm die gesamte Masse M vereinigt, und als griffen die resultierenden Kräfte in diesem Punkt an. Spezialfall: nur innere Kräfte ⇒ vM = const. Der Schwerpunkt eines abgeschlossenen Systems wird durch innere Kräfte nicht verändert (Satz von der Erhaltung des € Massenmittelpunktes). Versuch: LKT + 4 Magnetpucks Beispiel: Explodierende Granate: Der Schwerpunkt der Sprengstücke setzt die Bahn der Granate unbeirrt fort. 64 Prüfungsfrage: Lüge oder Wahrheit? Münchhausen sagte, er hätte sich und sein Pferd an seinem Zopf aus dem Sumpf herausgezogen. Stimmt das? Massenmittelpunkt eines Festkörpers: Starrer Körper ⇒ Anhäufung von Massenpunkten, die ihre gegenseitige Lage mit der Zeit nicht ändern, d. h. der Massenmittelpunkt bleibt unverändert. Teile Körper in Massenelemente auf: Δmi = ρΔVi Dimension: ρ heißt Massendichte, V ist das Volumen Masse / Volumen N € rM = Einheit: kg m3 ∑ Δm r ii i=1 N ∑ Δm i 1 N = ∑ ri ρΔVi M i=1 € i=1 Im Limit ΔVi ⇒ 0 1 rM = ∫ r ρΔV M € Für uniforme Massenverteilung ρ = const. liegt der Massenmittelpunkt auf der Symmetrieachse. € Versuch: Versuch: Massenmittelpunkt Stab Massenmittelpunkt komplexer Körper Karton, Deutschland Massenmittelpunkt braucht nicht im Körper liegen. M heißt auch Massenschwerpunkt 65