Einführung in die Astronomie und Astrophysik II
Werbung

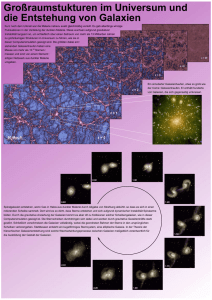
SS 2005 4 Einführung in die Astronomie und Astrophysik II Extragalaktische Physik 4.1 Überblick Galaxien bilden die fundamentalen Bausteine des beobachtbaren Universums. Sie sind von den Größenordnungen ihrer physikalischen Parameter unserer Milchstraße vergleichbar, trotzdem gibt es eine Vielzahl struktureller Formen. Die Komposition reicht von Galaxien, die nahezu vollständig aus Gas bestehen bis zu Galaxien, die nur aus Sternen ohne interstellares Medium bestehen. Galaxien gruppieren sich zu Haufen und Superhaufen. Tabelle 1 stellt die wichtigsten Parameterbereiche zusammen. Parameter Unterer Bereich Oberer Bereich Leuchtkraft 105 LSonne 1012 LSonne Leuchtende Masse 107 MSonne 1013 MSonne 0.5 kpc 30 kpc Radius Tabelle 1: Größen und Dimensionen von Galaxien. 4.2 Extragalaktische Entfernungsbestimmungen Der Nachweis daß Galaxien Körper sind, welche nicht unserer Milchstraße angehören, gelang Edwin Hubble im Jahre 1924. Er konnte einzelne Sterne in der Andromeda-Galaxie (M31) und anderen auflösen und einige Sterne mit bekannter absoluter Helligkeit identifizieren und somit das Entfernungsmodul zu M31 berechnen. Damit war die Grundlage der extragalaktischen Entfernungsbestimmung gelegt. Die Zuordnung der Galaxien zu übergeordneten Strukturen erfordert eine Reihe von Methoden der Entfernungsbestimmung, die hier zunächst vorgestellt werden sollen. Den Ausgangspunkt finden extragalaktische Methoden in den innerhalb der Milchstraße verwendeten, basieren also letztendlich auf astrometrischen Parallaxen und stellarstatistischen Methoden. Galaxien sind für trigonometrische Parallaxen viel zu weit entfernt. Als Entfernungsindikatoren müssen Objekte herangezogen werden, deren Leuchtkraft entweder bekannt oder anderweitig bestimmbar sind. Aus galaktischen Einführung_4.1-5_2005.sxw Seite 4-1 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Untersuchungen sind die absoluten Helligkeiten von besonderen Sternenklassen gut verstanden, welche sich wegen ihrer hohen Leuchtkraft als extragalaktische „Standardkerzen“ eignen. Objektklasse Abs. Helligkeit [m] Reichweite δ Cephei – Variable -2 ≥ MV ≥ −7 25 Mpc RR Lyrae – Variable MV ~ 0.7 1 Mpc Überriesen (O, B, A) -5 ≥ MV ≥ −10 10 Mpc Planetarische Nebel M[O III] ≥ −5 20 Mpc Supernovae (Ia) MV ≥ −19.5 5000 Mpc Tabelle 2: Wichtige extragalaktische Standardkerzen und ihre Reichweite. • Perioden-Helligkeitsbeziehungen: diese gibt es für einige der in Kapitel 2 vorgestellten pulsierenden Veränderlichen. Prominenteste Vertreter sind die der Population I angehörenden Cepheiden (nach δ Cephei) mit absoluten Helligkeiten von M = -2 ... -7 und Perioden zwischen 1 ... 50 Tagen. Sehr ähnlich, aber absolut um 1.5 mag schwächer sind die W VirginisSterne der Population II. Letztere waren es, welche E. Hubble tatsächlich in M31 gemessen, aber mit den klassischen Cepheiden verwechselt hatte; es dauerte 30 Jahre bevor W. Baade den Irrtum erkannte und den Abstand zu M31 auf nunmehr 690 kpc mehr als verdoppelte. Heute gültige Perioden-Helligkeitsbeziehungen schließen die chemische Zusammensetzung ein. Man kann Entfernungsmoduln bis zu m - M = 29 mag messen und damit bis zu 6 Mpc vordringen. • Lichtkurven von Novae: diese stellen Standardkerzen dar, sofern sie denen galaktischer Novae gleichen. • Hellste nichtveränderliche Sterne: haben absolute Leuchtkräfte M = -10, ebenso wie • Hellste Kugelsternhaufen. • H II - Regionen: lassen sich bei bekanntem Winkeldurchmesser nach genauer Eichung sehr gut in Entfernungen bis m - M = 33 bzw. 40 Mpc verwenden. Einführung_4.1-5_2005.sxw Seite 4-2 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II • Supernovae: haben sehr große absolute Helligkeiten von MB,max = -19.7 ± 0.3 mag (bei einer Hubble-Konstanten H0 = 50 km s-1 Mpc-1; s. u.) und eignen sich daher für Entfernungen bis 1 Gpc. Bevorzugt sind Typ I Supernovae in elliptischen Galaxien, welche nur geringer Extinktion in der Muttergalaxie unterliegen. Die geringe Häufigkeit von Supernovae (1 Galaxie-1 (100 y)-1) wird bei großen Galaxienhaufen durch die Zahl der Mitglieder wieder aufgehoben. Mit Hilfe der Theorie der Sternatmosphären kann man nach der Methode von Baade und Wesselink die Entfernung der Supernovae auch direkt bestimmen. Der gemessene spektrale Strahlungsstrom bei einem Sterndurchmesser R und seiner Entfernung zum Beobachter r beträgt f λ = Fλ (R r )2 (s. Gl. 2.8) für einen Strahlungsstrom Fλ an der Sternoberfläche. Ändert sich der Radius mit der Zeit, so läßt sich die Entfernung eliminieren durch den Quotienten zweier Messungen zu verschiedenen Zeiten. Anhand der Radialgeschwindigkeiten kann man andererseits durch Integration die Änderung des Radius in absoluten Einheiten ermitteln und somit für die Entfernung r lösen. Den Strahlungsstrom Fλ bestimmt man aus der Theorie der Sternatmosphären. • Helligkeiten der Galaxien: sind mit geringerer Genauigkeit als Standardkerzen verwendbar. Dazu werden morphologische Kriterien sowie statistische Eigenschaften (z. B. hellste Galaxie eines Haufens) herangezogen. • Tully-Fisher - Relation: stellte ursprünglich einen Zusammenhang zwischen der über die Scheibe integrierten, auf Inklination korrigierten Dopplerbreite ∆V0 der 21cm - Linie und der Masse M von Spiralgalaxien her. In den späten 70er Jahren wurde ein enger Zusammenhang zwischen der Leuchtkraft im Nahen Infrarot und der Kreisbahngeschwindigkeit von Sternen in den Scheiben entdeckt: v Scheibe L ≈ 3⋅1010 L Sonne 200 km s­1 4 . • Kosmologische Rotverschiebung: bedeutet die systematische Zunahme der Rotverschiebung von Spektrallinien von Galaxien mit deren Entfernung. Sie wird kosmologisch duerch eine Expansion des Universums gedeutet. In der "näheren" Um∆λ gebung ist das zugrundeliegende Gesetz linear: vR = λ c = H 0 r mit dem Hubble-Parameter H0. Der Hubble-Parameter 0 muß empirisch bestimmt werden und beträgt z. Z. 70 km s-1 Mpc-1 mit einer Genauigkeit von ca. 10%. Distanzschätzungen basierend auf Rotverschiebungen reichen am weitesten in das Universum. Einführung_4.1-5_2005.sxw Seite 4-3 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II 4.3 Klassifikation von Galaxien Der durch die Atmosphäre und das Zodiakallicht hervorgerufene natürliche Hintergrund begrenzt die Empfindlichkeit für Objekte mit geringer Flächenleuchtkraft, wie Galaxien. Man kann daher nur die hellsten Bereiche vieler Galaxien beobachten - Auswahleffekte! Anhand ihrer Morphologie unterscheidet man • Elliptische Galaxien • Linsenförmige Galaxien • Spiralgalaxien • Balkenspiralgalaxien • Irreguläre Galaxien Elliptische Galaxien erscheinen als elliptische Konzentrationen von Sternen ohne Anzeichen eines interstellaren Mediums oder von kürzlicher Sternentstehung. Man teilt sie gemäß der (projizierten) Elliptizität in die Klassen E0, E1, ... E7 ein, wobei E0 scheinbar kugelförmig sind und bei E7 die scheinbare kurze Halbachse 30% der langen Halbachse betragen. Eine Sonderform sind elliptische Riesengalaxien (Klasse cD), elliptische Galaxie mit einem großen, leuschtschwachen Halo aus Sternen. Linsenförmige Galaxien (Typ S0) bestehen aus einer elliptischen Komponente mit einer flachen Scheibe aus Sternen ohne Anzeichen von Spiralen sowie nur geringen Anteilen interstellaren Mediums. Spiralgalaxien haben eine zentrale elliptische Komponente ("bulge") sowie eine Scheibe aus Sternen. Zusätzlich gibt es eine dünne Scheibe aus interstellarem Medium, welches eine Spiralstruktur zeigt. Dort findet Sternentstehung statt. Balkenspiralgalaxien weisen zudem einen prominenten zentralen Balken auf. Man unterscheidet je nach Ausbildung der zentralen Ellipse und der Spiralen die Typen Sa ... Sb ... Sc bzw. Sba ... SBb ... SBc. Die Milchstraße ist klassifiziert als Typ Sbc (Zwischentyp zwischen Sb und Sc); jüngere Studien zeigen aber die schwache Ausbildung eines Balkens. Irreguläre Galaxien lassen sich von der Struktur keiner der bisherigen Klassen zuordnen. Sie enthalten häufig Staub und zeigen Sernbildung. Einführung_4.1-5_2005.sxw Seite 4-4 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II 4.3.1 Elliptische Galaxien Struktur: die Helligkeitsverteilung elliptischer Galaxien ist im wesentlichen eine Funktion des (u. U. elliptisch verzerrten) Radius. Eine gute empirische Annäherung an gemessene Verteilungen der Flächenhelligkeit I ist gegeben mit dem de Vaucouleur'schen Gesetz: r I ( r) = − 3.334 − 1 . (4.1) Ie r e Die Größen re und Ie sind so gewählt, daß die Hälfte der Gesamtleuchtkraft der Galaxie innerhalb des Radius re auftritt und die Flächenhelligkeit dort den Wert Ie hat. Typische Werte sind 1 ... 10 kpc bzw. 20 ... 23 mag arcsec-2. In den äußeren Gebieten einiger Galaxien kann es zu Abweichungen von (4.1) kommen; bei Zwerggalaxien ist der Abfall u. U. stärker, bei den massereichsen elliptischen Riesengalaxien dagegen schwächer. Sowohl die Elliptizität als auch die Orientierung der Linien konstanter Helligkeit kann für eine gegebene Galaxie eine Funktion der Helligkeit sein; daraus läßt sich schließen, daß die Struktur derselben komplizierter ist, als es den Anschein hat. Unter der Voraussetzung der Rotationssymmetrie kann man aus der Helligkeitsverteilung auf die dreidimensionale Struktur bei elliptischen Galaxien schließen; dies kann man am einfachsten am, Beispiel kugelförmiger Galaxien erläutern. Bezeichnen wir mit Iˆ( ρ ) die dreidimnsionale Verteilung der Leuchtkraftdichte, die nur eine Funktion des Abstandes vom Zentrum ρ sei. Die beobachtete Flächenhelligkeit I(r) ist eine Funktion des Abstandes r von der Projektion des Zentrums an die Himmelssphäre, und ist gegeben mit dem Integral von Iˆ( ρ ) längs der Sehlinie log10 I (r ) = +∞ ∫ Iˆ(ρ ) dz , (4.2) −∞ wobei dz ein Längenelement der Sehlinie ist. Es gilt r 2 + z 2 = ρ 2 und durch Vertauschung der Variablen erhält man für (4.2) ∞ I ( r ) = 2 ∫ Iˆ ( ρ ) r Einführung_4.1-5_2005.sxw ρ 2 ρ −r 2 dρ . (4.3) Seite 4-5 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Diese Gleichung läßt sich allgemein für Iˆ( ρ ) lösen, und man erhält ∞ 1 dI ( r ) dr . π ∫ dr 2 2 r −ρ ρ Iˆ( ρ ) = − 1 (4.4) Die Gleichung (4.3) ist eine Abel'sche Integralgleichung. Man bezeichnet die Transformation zwischen einer symmetrischen Verteilung und ihrer Projektion nach (4.3) und (4.4) als Abel-Transformation. Führt man diese Transformation für elliptische Galaxien durch, so stellt man fest, daß die dreidimensionale Leuchtdichte sehr stark zum Zentrum konzentriert ist ("Galaxienkern"). Zusammensetzung: Das Spektrum einer Galaxie setzt sich aus den Spektren ihrer Mitgliedssterne zusammen. Aus verschiedenen spektralen Details (Stärken vieler Linien, breitbandige spektrale Verteilung) kann man auf die Massen, das Alter und die chemische Zusammensetzung der Sternpopulationen schließen (Populationssynthese). In Verbindung mit der Evolutionstheorie der Sterne kann man die Entwicklung der Leuchtkraft der Galaxie untersuchen. Demnach bestehen elliptische Galaxien praktisch ausschließlich aus Sternen, welche gleichzeitig vor 1010 Jahren gebildet wurden. Die meiste Leuchtkraft stammt von Roten Riesen, der Löwenanteil der Masse aber von Sternen mit M < MSonne. Da metallreiche Sterne bei gleicher Leuchtkraft röter sind als metallarme, deuten Verfärbungen auf die chemische Zusammensetzung hin. In diesem Sinne gibt es eine Farb-Helligkeitsbeziehung; hellere Galaxien sind auch röter. Die metallreichen elliptischen Galaxien haben sonnenähnliche Metallizitäten, die metallärmeren einen Faktor 100 weniger. Außerdem zeigen elliptische Galaxien einen Farbgradienten so daß die zentralen Bereiche metallreicher sind. Viele elliptische Galaxien enthalten kein interstellares Medium, obwohl ihre Sternpopulation welches produzieren müßte. Wenige zeigen Anzeichen von Sternentwicklung in ihrem Kern. Dynamik: aus den Spektren kann man durch Doppleranalyse Geschwindigkeitsverteilungen ableiten. Die Geschwindigkeiten der individuellen Sternen bestimmen Linienbreiten, eine Rotation um das Zentrum bewirkt systematische Verschiebungen als Funktion der Position. Es zeigt sich, daß eine Rotationskomponente nicht eine Elliptizität erklärt - es gibt also keine "Rotationsellipsoiden". Rotationsgeschwindigkeiten sind oft geringer als Geschwindigkeitsdispersionen, beide liegen im Bereich von wenigen 100 km s-1. Einführung_4.1-5_2005.sxw Seite 4-6 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II 4.3.2 Spiralgalaxien Der zentrale Bereich der Spiralgalaxien ähnelt in Struktur und Helligkeitsverteilung einer elliptischen Galaxie. Die stellare Scheibenkomponente hat eine Helligkeitsverteilung der Form r I ( r ) = I 0 exp − . (4.5) r0 Die Flächenhelligkeit der Scheibe ist typischerweise 21 ... 22 mag arcsec-2 und der Radius r0 beträgt zwischen 1 und 5 kpc. Das Verhältnis der Helligkeiten von Zentralbereich und Scheibe ist etwas kleiner als 1 für den Typ Sc und etwas größer für "frühere" Typen. Die Dicke der Scheiben ist typischerweise 1.2 kpc. Der Anteil an interstellarem Medium variiert nach Typ zwischen ca. 2% für Sa und 10% für Sc, bis zu 15% oder mehr für irreguläre Galaxien. Aufgrund von Radiomessungen ist bekannt, daß das Gas auf eine nur 200 pc dicke Scheibe begrenzt ist, welche sich allerdings erheblich über die sichtbare Scheibe hinaus ausdehnen kann. Im Zentrum gibt es ein "Loch" von wenigen kpc Durchmesser. Zusammensetzung: der Zentralbereich ist ähnlich wie elliptische Galaxien zusammengesetzt. Die Zusammensetzung des Gases läßt sich anhand der Emission von H II - Regionen studieren. Der Metallgehalt nimmt zum Zentrum ebenfalls zu, allerdings ist die Variation zwischen Galaxien groß. Dynamik: die Rotationskurven der Spiralgalaxien ähnelt der unserer Milchstraße. Im Zentralbereich wächst die Rotationsgeschwindigkeit proportional zum Radius ("fester Körper") und ist in der Scheibenregion nahezu konstant. "Frühere" Galaxientypen (Sa) haben höhere Geschwindigkeiten um 300 km s-1 als spätere, um 200 km s-1. Spiralstruktur: die Spiralarme sind relativ helle Objekte. Einige Galaxien haben zwei ausgeprägte, durchgehende Arme, andere Galaxien viele kurze Fragmente. Die Arme öffnen sich fast immer in Gegenrichtung zur Rotation. Man sieht die Spiralstruktur am besten am interstellaren Staub, den H II-Regionen und an jungen Sternen. Staubwolken gibt es an den inneren Rändern der Spiralarme, an deren Rändern Sternentstehungsgebiete. Die Häufigkeit der Spiralen deutet darauf hin, daß es sich um ein langlebiges Phänomen handeln muß. Neuere theoretische Studien zufolge handelt es sich um spiralige Dichtewellen, welche den Kollaps der Staubwolken und damit die Sternentstehung hervorrufen. Bewegungen innerhalb der Spiralarme lassen sich mit der 21cm-Radiostrahlung messen. Die Entdeckung Einführung_4.1-5_2005.sxw Seite 4-7 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II der für die Dichtewellentheorie charakteristischen Geschwindigkeitsfelder steht aber noch aus. Die Ursache der Spiralen sowie der Balken ist weiterhin unklar. Links: Spiralnebel M 101 mit hoher Flächenhelligkeit. Rechts: Spiralnebel Malin 1 mit geringer Flächenhelligkeit. Einführung_4.1-5_2005.sxw Seite 4-8 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Spiralnebel M 81 im sichtbaren Spektralbereich (links) und im infraroten (rechts Komposit, unten einzelnen Wellenlängen). Einführung_4.1-5_2005.sxw Seite 4-9 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II 4.4 Massen- und Leuchtkraftbeziehungen Die integrale Leuchtkraft L einer Galaxie bestimmt man empfindlichkeitsbedingt bis zu einem Schwellenwert der Flächenhelligkeit (z. B. 26.5 mag arcsec-2). Damit werden integrale Leuchtkräfte eine etwas willkürliche Größe. Insbesondere die schwächer leuchtenden Außenbereiche werden oft nicht erfaßt. Die Leuchtkraft ist für alle Galaxientypen sehr variabel, sie hängt vermutlich von der Gesamtmasse einer Galaxie ab. Ähnlich wie bei Sternen bestimmt man die Verteilungsfunktion Φ(L) der Galaxienzahl in Abhängigkeit ihrer absoluten Leuchtkraft pro Volumenelement. Dies ist möglich, wenn man die Entfernungen der Galaxien kennt (s. unten). Eine allgemein verwendete Verteilung ist Schechter's Verteilungsfunktion α [ ] L L L Φ(L ) = Φ * exp − L L* d . * * L (4.6) Die Parameter Φ*, L*, und α werden experimentell bestimmt. Nach den Beobachtungen ist α = -1.1, damit nimmt die Häufigkeit leuchtschwacher Galaxien zu. Oberhalb von L* = -21 mag nimmt die Häufigkeit stark ab (die absolute Leuchtkraft der Milchstraße ist -20.2). Der Parameter Φ* entspricht einer Raumdichte und ist örtlich stark variabel. Die Raumdichte von Galaxien mit L > L* beträgt 3.5 10-3 Mpc-3, der mittlere Abstand dieser Galaxien ca. 4 Mpc. Da die Zahl leuchtschwächerer Galaxien wesentlich höher ist, ist der mittlere Abstand von der Größenordnung der Durchmesser der Galaxien. Die Masse der Galaxien spielen eine große Rolle für die Kosmologie. Galaxienmassen lassen sich indirekt aus ihrer Dynamik sowie der Dynamik der Galaxienhaufen bestimmen. Daraus lassen sich Masse-Leuchtkraft-Beziehungen M/L (in Einheiten der Sonnemasse und -Leuchtkraft) ableiten. In der Umgebung der Sonne ist M/L = 3. Für elliptische Galaxien kann man die potentielle Energie - und damit die Masse - aus der aus Linienbreiten gewonnenen Geschwindigkeitsdispersion ∆V mit Hilfe des Virialsatzes bestimmen. Für ein System im Gleichgewicht gilt für die po-tentielle Energie U und die kinetische Energie T der Zusammenhang 2T + U = 0. Wegen der geringen Rotation ist T = M/2 (∆V)2. Die potentielle Energie ist gegeben mit U = -G M2 / (2R). Damit ist M = 2 (∆V)2 R / G. Für helle elliptische Galaxien ergibt sich innerhalb von Radien R von 10 kpc Massen von bis zu 1013 Sonnenmassen und ein Wert M/L = 10. Einführung_4.1-5_2005.sxw Seite 4-10 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II In den äußeren Bereichen der Scheiben von Spiralgalaxien ist die Rotationsgeschwindigkeit - welche die kinetische Energie dominiert - unabhängig vom Abstand. Damit ist die von einem Radius R umschlossene Masse M(R) direkt zu R proportional. M/L beträgt hier je nach Typ zwischen 4 ... 8. Gesamtmassen betragen bis zu 1012 Sonnenmassen. Aus der Dynamik einzelner Galaxien in größeren Ansammlungen kann man auf das Vorhandensein nichtleuchtender Materie in erheblichem Ausmaß schließen. Hier ergeben sich Werte von M/L zwischen 20 ... 30, entsprechend einem mittleren Abstand zwischen Galaxien von 50 kpc. Die Dynamik der Galaxienhaufen in Superhaufen läßt auf noch höhere Werte von bis zu 200 schließen. Offenbar nimmt der Anteil nichtleuchtender Materie mit größerer Skala zu. Die Natur dieser Materie ist bislang völlig spekulativ und wird als missing mass problem bezeichnet. 4.5 Dynamischer Aufbau von Galaxien 4.5.1 Wie stark beinflussen sich Sterne gegenseitig? Zeitraum ∆t zwischen zwei „nahen Vorbeiflügen“ von Sternen, näher als „kritischer Abstand“ R: t≈ R 2 n Stern v ­1 nStern: Sterndichte, v : mittlere Relativgeschwindingkeit der Sterne. (4.7) Setze R zu dem Abstand, für welchen das Potential der Gravitation zwischen den Kollisionspartnern das allgemeine Potential der Galaxie überwiegt. Mit dem Virialsatz: G M 1 M 1 M 1 v 2 2G M 2 (4.8) R krit = 2 R 2 v Für eine Sonnenmasse ergibt sich ein kritischer Radius von etwa 2 1011 m (1.3 AU). Die Kollisionszeitskala ist dann v3 v ≈ 4⋅109 a t = 2 4 G M 2 n Stern [ km s­1 ] Einführung_4.1-5_2005.sxw 3 M2 M Sonne ­2 Seite 4-11 n Stern [ pc­3 ] ­1 (4.9) 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Für eine Sonnenmasse sowie der mittleren Dichte der Sonnenumgebung und v =40 km s­1 wird ∆t etwa 1015 Jahre. Eine Galaxie kann daher näherungsweise als ein Ensemble kollisionsfreier Teilchen betrachtet werden. Genauer betrachtet muss man aber den Impulsübertrag zwischen Sternen auch bei weiten Vorbeiflügen berücksichtigen, da sich Störungen des Geschwindigkeitsvektors kumulieren. Nach einer gewissen Zeit wird die Geschwindigkeitsverteilung „relaxiert“ sein, d. h., von einer ursprünglichen Verteilung keine Hinweise mehr vorhanden sein. Integriert man den Impulsübertrag bis zu einem Maximalabstand Rmax und betrachtet den Zeitpunkt, bis zu welchem die Störungen dieselbe Größenordnung wie die Originalgeschwindigkeit erreichen, so ergibt sich t relax = t ln R max / R crit ­1 . (4.10) 4.5.2 Spiralstruktur Über die Ursache der Struktur der Scheiben von Spiralnebeln ist lange gerätselt worden. Di Sirltrktur manifestiert sich in der Dichte des interstellaren Mediums, insbesondere des Staubs, sowie in der Verteilung von jungen Sternen und Sternentstehungsgebieten. Fast immer ist die Spirale entgegen der Rotationsrichtung der Scheibe geöffnet. Eine Spiralstruktur würde sich fast natürlich aus der konstanten Rotationsgeschwindigkeit der Scheibe (im äußeren Teil) ergeben, v rot r = const r = v rot r const = r r (4.11) Eine anfänglich radial verlaufende Struktur (ϕ = ϕ0) wird nach einer Zeit t spiralförmig verzerrt: r , t = 0r t (4.12) Der Winkel i, den die Struktur mi derdaen Richtung nach der Zeit t bildet, ist tan i = ∣ ∣ ∣ ∣ d d 1 dr =s t =r dr dr r d tan i (4.13) Setzt man die Werte für die Milchstraße ein (vrot = 220 km s-1, r = 10 kp, t = 1010 a), so erhält man viel zu kleine Anstellwinkel. Einführung_4.1-5_2005.sxw Seite 4-12 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Die Spiralen müssen daher andere Ursachen haben - Dichtewellen. Heutige Modelle betrachten Simulationen mit mehreren Millionen Teilchen, um Dichtewellen im Computer nachzuvollziehen. Einführung_4.1-5_2005.sxw Seite 4-13 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Elliptische Galaxien - M87 Einführung_4.1-5_2005.sxw Seite 4-14 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Sa E Einführung_4.1-5_2005.sxw Sb Sc Sd S0 Seite 4-15 27.06.05 SS 2005 Einführung_4.1-5_2005.sxw Einführung in die Astronomie und Astrophysik II Seite 4-16 27.06.05 SS 2005 Einführung in die Astronomie und Astrophysik II Î(ρ) I(r) ρ r Einführung_4.1-5_2005.sxw Seite 4-17 z 27.06.05