Klassenarbeit Nr

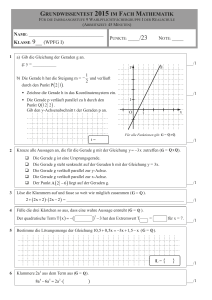
Lineare Funktionen: Übungen
1. Zeichne (direkt) folgende Geraden in ein Koordinatensystem.
1
3
g1: y = − ⋅ x − 2
g2:y = 3
g3 : y = ⋅ x + 1
g 4 : x = −2
4
2
g5 : y = 2 ⋅ x − 3
2. Gib die Gleichungen der
eingezeichneten
Geraden in Normalenform an.
3. a.) Ermittle rechnerisch die Gleichung (Normalenform) der Geraden, die durch die Punkte A
(3/6) und B (-2/5) geht.
b.) Gib einen Punkt an, der auf der Geraden g: 2x + 3y - 2 = 0 liegt.
3 5
Liegt der Punkt P(− / ) auf der Geraden g ? Gib einen Punkt an, der nicht auf g liegt.
2 3
Wie lautet die Steigung der Geraden g ? Wo schneidet g die y-Achse ?
c.) Welche Gerade durch den Nullpunkt ist parallel zu g ?
4. Beschreibe das abgebildete Geradenbüschel
durch
eine Gleichung in Normalenform.
Auf welcher Geraden liegt der Punkt P (4/-6) ?
5. In welchem Punkt schneidet die Gerade y = -3x + 8
a.) die y-Achse
b.) die x-Achse
c.) die Gerade y = 2x - 7 ?
6. Von einer Wetterstation, die sich auf der Spitze eines Berges befindet, wird ein Wetterballon
zum (gleichmäßigen) Aufsteigen gebracht. Nach 2 Minuten hat er eine Höhe von 1600 Metern über dem Meeresspiegels erreicht, nach 7 Minuten befindet er sich in 3300 m Höhe.
a) Erstelle eine Funktionsgleichung zur Funktion
Zeit nach dem Start (in Minuten) → Höhe des Ballons über dem Meeresspiegel (in m).
b) In welcher Höhe befindet sich der Ballon nach 20 Minuten?
c) Wann beträgt seine Höhe 4830 Meter?
d) Wie hoch ist der Berg, auf dessen Spitze sich die Wetterstation befindet?
e) Die Hülle des Ballons platzt in einer Höhe von 20 km, weil sie dem Druck nicht mehr
standhalten kann.
Einer der Meteorologen meint, dass dies erst mindestens eine Stunde nach dem Start geschehen wird. Was meinst du?
7. Bestimme die Gleichung in der Normalform für diejenige Gerade, die durch den Punkt P geht
und zu der Geraden g
a) parallel
b) orthogonal (senkrecht) ist.
x
g: y = - − 2 ,
3
P (2 | -4)
8. M ist der Mittelpunkt der Strecke AB . Bestimme die fehlenden Koordinaten.
a) A (xa | ya ), B (-1 | -2), M (2 | -4)
b) A (7 | ya ), B (xb | -1), M (0 | 0)
9. a) Gegeben ist die Gerade g mit der Gleichung 4x + 5y = 6. Gib eine Orthogonale zu g an.
Bestimme die Orthogonale zu g durch P (-0,5/1) .
b) Die Punkte A (0/0), B (6/0) und C (x/y) sollen ein gleichschenkliges Dreieck mit der Basis
AB bilden. Wie muss x und y gewählt werden, damit die Schenkeln (AC, BC) die Länge
45 haben ?
10.a) Welche Punkte auf den Koordinatenachsen haben von P (-1/1) den Abstand 2 ?
b) Wie muss y gewählt werden, damit P (2/y) vom Nullpunkt den Abstand 4 hat ?
11.Welchen Winkel schließt die Gerade 3x + 4y = 7 mit der a)
x-Achse b) y-Achse ein ?
12.Bestimme den Schnittpunkt S der Diagonalen des Vierecks mit den Eckpunkten
A (2 | 1), B (7 | 2), C (7 | 6), D (4 | 5).
Unter welchem Winkel schneiden sich die Diagonalen?