Unterrichtskonzept zur Einführung von Ebenen in der Q12 Thomas

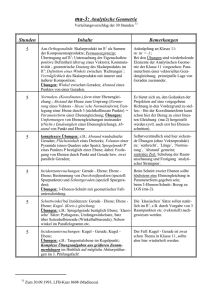
Unterrichtskonzept zur Einführung von Ebenen in der Q12
Oberstufenseminar
Dozent: Andreas Eberl
Thomas Grill
12.12.11
Lehrplanvorgaben




Beschreibung von Geraden und Ebenen durch Gleichungen
Lagebeziehungen: gegenseitige Lage von Geraden, von Ebenen sowie von Geraden und
Ebenen zueinander
Abstands- und Winkelbestimmungen, insbesondere unter Verwendung der Hesse'schen
Normalenform
Anwendungen in Sachzusammenhängen
Vorwissen:
11. Klasse:
 Vektoren
 Skalarprodukt
 Vektorprodukt
12. Klasse:
 Lineare Ab- und Unabhängigkeit von Vektoren
 Geradengleichung in Parameterform
Mögliche inhaltliche Vorgehensweise






Parametergleichung der Ebene
Normalenformen der Ebenengleichung
Besondere Lagen von Ebenen im Raum
Lagebeziehung zwischen Gerade und Ebene
3 Möglichkeiten:
1. Schnittpunkt (Sonderfall: g senkrecht auf E)
2. g echt parallel zu E
3. g liegt in E
Lagebeziehung zwischen Ebenen
3 Möglichkeiten:
1. Schnittgerade
2. Ebenen sind echt parallel zueinander
3. Ebenen sind identisch
Abstände
1 Abstand Gerade – Punkt
2 Abstand Ebene – Punkt
Abstand zweier windschiefer Geraden

Winkel
Ausgewählte „Problemstellen“
a)Übergang Parameterform  Normalenform
o
Geometrischer Ansatz:
o
Algebraischer Ansatz
𝐴𝑋⃗ ⊥ 𝑛⃗ ⇔ 𝑛⃗ ∘ 𝐴𝑋⃗ = 0 ⇔ 𝑛⃗ ∘ (𝑋⃗ − 𝐴⃗) = 0
b) Hesse´sche Normalenform und
Herleitung der Formel zur Abstandsbestimmung
𝑑 = 𝐴𝑃⃗ ⋅ 𝑐𝑜𝑠𝜑 = 𝐴𝑃⃗ ⋅
n ⃗ ∘ 𝐴𝑃⃗
= n ⃗ ∘ 𝐴𝑃⃗
|n ⃗| ⋅ 𝐴𝑃⃗
Schülerschwierigkeiten / Fehlvorstellungen
Zwei Sichtweisen der Analytischen Geometrie in Bezug auf Ebenen:
1) Ebene als Punktmenge
2) Ebene als ganzheitliches und konkret- gegenständliches Objekt  führt zu Problemen
Probleme bei
 der geometrischen Deutung von 𝑛
 der Frage, ob zwei Ebenengleichungen dieselbe Ebene beschreiben