13. Binäre Suchbäume
Werbung

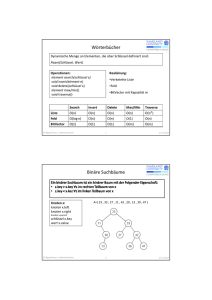
13. Binäre Suchbäume Binäre Suchbäume realiesieren Wörterbücher. Sie unterstützen die Operationen 1. Einfügen (Insert) 2. Entfernen (Delete) 3. Suchen (Search) 4. Maximum/Minimum-Suche 5. Vorgänger (Predecessor), Nachfolger (Successor) Laufzeit für alle Operationen proportional zur Höhe des Baums. Später spezielle Suchbäume bei denen Höhe logarithmisch in Anzahl der Knoten ist. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 1 Suchbaum-Eigenschaft (1) Binäre Suchbäume sind binäre Bäume. Bestehen aus Objekten mit Feldern für Verweis 1. p auf Eltern 2. right auf rechtes Kind 3. left auf linkes Kind Zusätzlich Feld key für Schlüssel, dabei sind Schlüssel natürliche Zahlen. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 2 Suchbaum-Eigenschaft (2) Es gilt Suchbaum-Eigenschaft: Für jedes Objekt x und jedes Objekt y im linken Teilbaum von x gilt key[y] ≤ key[x]. Für jedes Objekt x und jedes Objekt y im rechten Teilbaum von x gilt key[y] ≥ key[x]. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 3 Binäre Bäume - Illustration root[T] / / / / / / / / / / SS 2006 / / / Datenstrukturen und Algorithmen 13.Binäre Suchbäume 4 Illustration von Suchbäumen 5 7 3 2 8 5 2 3 7 5 8 5 SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 5 Durchlaufen von Suchbäumen (1) Suchbaum-Eigenschaft erlaubt es, Schlüssel im Baum in sortierter Reihenfolge auszugeben. Dazu wird der Baum in Inorder durchlaufen. D.h. die Wurzel eines Teilbaums wird zwischen den Knoten des linken und des rechten Teilbaums ausgegeben. Alternativen Methoden, die Knoten eines Suchbaums zu durchlaufen, sind: 1. Postorder 2. Preorder SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 6 Durchlaufen von Suchbäumen (2) Inorder - Tree - Walk ( x ) 1 if x ≠ NIL 2 then Inorder - Tree - Walk (left [x ]) 3 print ( x ) 4 Inorder - Tree - Walk (right [x ]) Satz 13.1: Ist x Wurzel eines Baums mit n Knoten, so benötigt Algorithmus Inorder-Tree-Walk bei Aufruf mit Knoten x Zeit Θ(n). SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 7 Suchen in Suchbäumen Ziel: Finde in einem Suchbaum Knoten x mit Schlüssel k. Falls kein Knoten mit Schlüssel im Suchbaum enthalten, Ausgabe NIL. Tree - Search( x , k ) 1 if x = NIL ∨ k = key [x ] 2 return x 3 if k < key [x ] 4 then Tree - Search(left [x ], k ) 5 else Tree - Search(right [x ], k ) Aufruf bei Suche in Baum T mit Tree-Search(root[T],k). Lemma 13.2: Tree-Search hat Laufzeit Θ(h), wobei h die Höhe des Baums T ist. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 8 Suchen in Suchbäumen (2) 15 6 7 3 2 18 17 4 20 13 9 Suche nach Schlüssel 9: SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 9 Iteratives Suchen in Suchbäumen Iterative - Tree - Search( x , k ) 1 while x ≠ NIL ∧ k ≠ key [x ] 2 do if k < key [x ] 3 then x ← left [x ] 4 else x ← right [x ] 5 return x SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 10 Finden von Minimum/Maximum Ziel: Finde in einem Suchbaum Knoten x mit minimalem bzw. maximalem Schlüssel. Tree - Minimum( x ) 1 while left [x ] ≠ NIL 2 do x ← left [x ] 3 return x Tree - Maximum( x ) 1 while right [x ] ≠ NIL 2 do x ← right [x ] 3 return x Aufruf bei Baum T mit Tree-Minimum(root[T]) bzw. Tree-Maximum(root[T]). Lemma 13.3: Tree-Minimum und Tree-Maximum haben Laufzeit Θ(h), wobei h die Höhe des Baums T ist. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 11 Finden des direkten Nachfolgers(1) Ziel: Gegeben Suchbaum T und Knoten x mit Schlüssel k, finde Objekt mit nächst größerem Schlüssel (unter Annahme, dass alle Schlüssel unterschiedlich). Lemma 13.4: Besitzt x ein rechtes Kind, so ist der direkte Nachfolger von x der Knoten mit minimalem Schlüssel im rechtem Teilbaum von x. Besitzt x kein rechtes Kind, so ist der direkte Nachfolger von x der niedrigste Vorfahr von x, dessen linkes Kind ebenfalls ein Vorfahr von x ist (dabei ist ein Knoten Vorfahr von sich selbst). SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 12 Finden des direkten Nachfolgers (2) 15 6 7 3 2 18 17 4 20 13 9 Nachfolger von Schlüssel 13: SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 13 Finden des direkten Nachfolgers(3) Tree - Successor ( x ) 1 if right [x ] ≠ NIL 2 then return Tree - Minimum(right [x ]) 3 y ← p[x ] 4 while y ≠ NIL ∧ x = right [y ] 5 do x ← y 6 y ← p[y ] 7 return y Lemma 13.5: Tree-Search hat Laufzeit Θ(h), wobei h die Höhe des Baums T ist. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 14 Einfügen eines Elements (1) Idee: Finde Knoten mit höchstens einem Kind, für den einzufügender Knoten Wurzel des fehlenden Teilbaums werden kann. 6 11 3 2 9 4 8 13 10 Einfügen von Schlüssel 8 : SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 15 Einfügen eines Elements (2) Tree - Insert (T , z ) 1 y ← NIL 2 x ← root [T ] 3 while x ≠ NIL do y ← x 4 if key [z ] < key [x ] 5 then x ← left [x ] 6 7 else x ← right [x ] 8 p[z ] ← y 9 if y = NIL 10 then root [T ] ← z > Baum T war leer 11 else if key [z ] < key [y ] 12 then left [y ] ← z 13 else right [y ] ← z SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 16 Einfügen eines Elements (3) Lemma 13.6: Tree-Insert hat Laufzeit Θ(h), wobei h die Höhe des Baums T ist. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 17 Entfernen von Elementen (1) Betrachten beim Entfernen von Knoten drei Fälle: 1. Zu entfernender Knoten ist Blatt. 2. Zu entfernender Knoten besitzt nur ein Kind. 3. Zu entfernender Knoten besitzt zwei Kinder. Behandlung der drei Fälle: 1. Blatt kann einfach entfernt werden. 2. Knoten wird durch sein einziges Kind ersetzt. 3. Nutzen aus, dass direkter Nachfolger kein linkes Kind besitzt. Ersetzen Knoten durch direkten Nachfolger und entfernen Nachfolger wie in 2. aus seiner ursprünglichen Position. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 18 Entfernen eines Blattes 6 6 11 2 4 3 9 5 11 2 13 4 9 13 3 z SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 19 Entfernen eines Elements mit 1 Kind 6 z 3 4 11 2 4 SS 2006 6 9 13 3 11 5 9 13 5 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 20 Entfernen eines Elements mit 2 Kindern z z 6 9 6 11 2 11 2 y y 4 3 9 5 10 4 13 3 10 13 5 9 11 2 10 4 3 SS 2006 13 5 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 21 Entfernen von Elementen (2) Tree - Delete(T , z ) 1 if left [z ] = NIL ∨ right [z ] = NIL 2 then y ← z 3 else y ← Tree - Successor (z ) 4 if left [y ] ≠ NIL 5 then x ← left [y ] 6 else x ← right [y ] 7 if x ≠ NIL 8 then p[x ] ← p[y ] 9 if p[y ] = NIL 10 then root [T ] ← x 11 else if y = left [p[y ]] then left [p[y ]] ← x 12 13 else right [p[y ]] ← x 14 if y ≠ z 15 then key [z ] ← key [y ] 16 Satellitendaten von y werden nach z kopiert SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 22 Laufzeit von Einfügen und Entfernen Lemma 13.7: Tree-Delete hat Laufzeit Θ(h), wobei h die Höhe des Baums T ist. SS 2006 Datenstrukturen und Algorithmen 13.Binäre Suchbäume 23