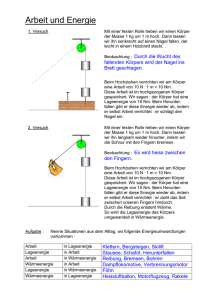
Wiederholung 4 Arbeit, Energie, Wirkungsgrad S. 1 1. 2. Nenne jew

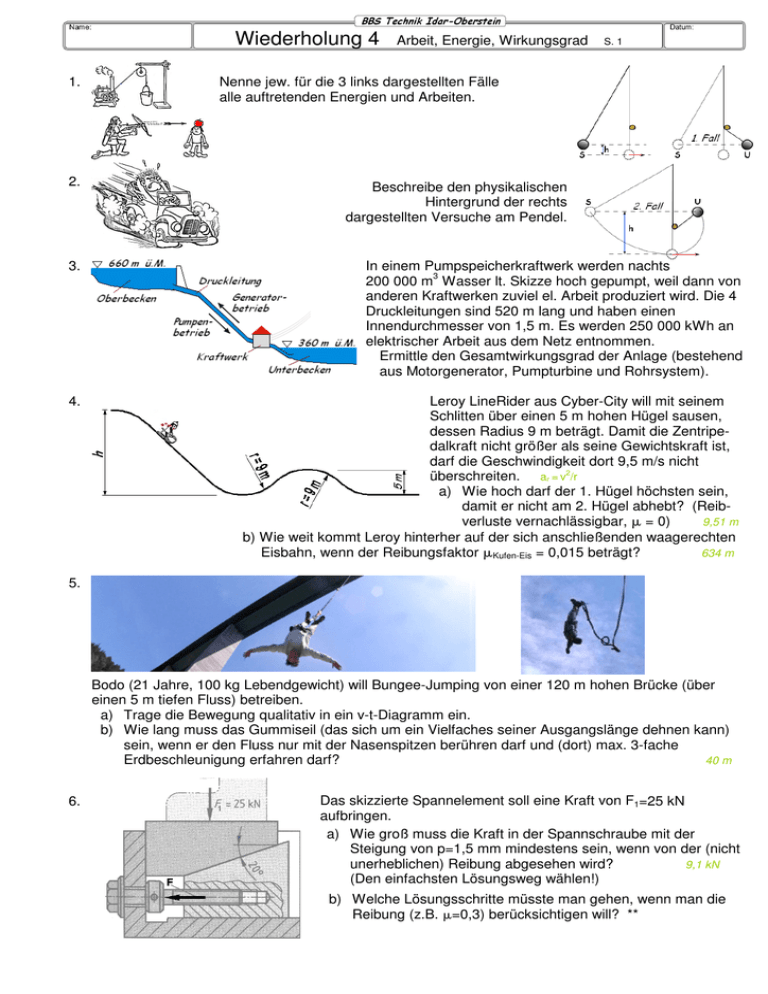
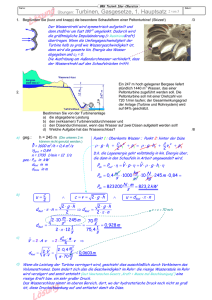
Wiederholung 4
1.
2.
3.
4.
Arbeit, Energie, Wirkungsgrad
S. 1
Nenne jew. für die 3 links dargestellten Fälle
alle auftretenden Energien und Arbeiten.
Beschreibe den physikalischen
Hintergrund der rechts
dargestellten Versuche am Pendel.
In einem Pumpspeicherkraftwerk werden nachts
200 000 m3 Wasser lt. Skizze hoch gepumpt, weil dann von
anderen Kraftwerken zuviel el. Arbeit produziert wird. Die 4
Druckleitungen sind 520 m lang und haben einen
Innendurchmesser von 1,5 m. Es werden 250 000 kWh an
elektrischer Arbeit aus dem Netz entnommen.
Ermittle den Gesamtwirkungsgrad der Anlage (bestehend
aus Motorgenerator, Pumpturbine und Rohrsystem).
Leroy LineRider aus Cyber-City will mit seinem
Schlitten über einen 5 m hohen Hügel sausen,
dessen Radius 9 m beträgt. Damit die Zentripedalkraft nicht größer als seine Gewichtskraft ist,
darf die Geschwindigkeit dort 9,5 m/s nicht
überschreiten. ar = v2/r
a) Wie hoch darf der 1. Hügel höchsten sein,
damit er nicht am 2. Hügel abhebt? (Reibverluste vernachlässigbar, µ = 0)
9,51 m
b) Wie weit kommt Leroy hinterher auf der sich anschließenden waagerechten
634 m
Eisbahn, wenn der Reibungsfaktor µKufen-Eis = 0,015 beträgt?
5.
Bodo (21 Jahre, 100 kg Lebendgewicht) will Bungee-Jumping von einer 120 m hohen Brücke (über
einen 5 m tiefen Fluss) betreiben.
a) Trage die Bewegung qualitativ in ein v-t-Diagramm ein.
b) Wie lang muss das Gummiseil (das sich um ein Vielfaches seiner Ausgangslänge dehnen kann)
sein, wenn er den Fluss nur mit der Nasenspitzen berühren darf und (dort) max. 3-fache
Erdbeschleunigung erfahren darf?
40 m
6.
Das skizzierte Spannelement soll eine Kraft von F1=25 kN
aufbringen.
a) Wie groß muss die Kraft in der Spannschraube mit der
Steigung von p=1,5 mm mindestens sein, wenn von der (nicht
unerheblichen) Reibung abgesehen wird?
9,1 kN
(Den einfachsten Lösungsweg wählen!)
b) Welche Lösungsschritte müsste man gehen, wenn man die
Reibung (z.B. µ=0,3) berücksichtigen will? **
Wiederholung 4
1.
Arbeit, Energie, Wirkungsgrad
S. 2
Nenne jew. für die 3 links dargestellten Fälle
alle auftretenden Energien und Arbeiten.
2.
Beschreibe den physikalischen
Hintergrund der rechts
dargestellten Versuche am Pendel.
1.a) chemische Energie (in der Kohle) Wärme (durch Verbrennung) Arbeit (Dampf o. Gas
treibt Kolben an: Gewicht wird angehoben) Lageenergie
1.b) chemische Energie im Körper von Wilhelm Tell Arbeit (Muskel spannt Armbrust) Spannenergie (Beschleunigungs-)Arbeit kinetische Energie (Reib-)arbeit im Apfel „Wärme“ (korrekt: innere Energie)
1.c) chemische Energie (Beschleunigung-)Arbeit kinetische Energie (Reib-)arbeit innere
Energie
2. Fall 1: Das Pendel verliert keine Energie. Deshalb steigt das Pendelgewicht wieder so hoch, wie
vorher. (Lageenergie Bewegungsenergie Lageenergie ... und wieder zurück ...)
2. Fall 2: Wie Fall 1
Gerät das Hindernis noch tiefer, so ist das Seil zu kurz um die Ausgangshöhe zu
erreichen Pendel überschlägt sich am Hindernis und wickelt sich auf, bis es irgendwo
reibt.
3.
In einem Pumpspeicherkraftwerk werden nachts
200 000 m3 Wasser lt. Skizze hoch gepumpt, weil dann von
anderen Kraftwerken zuviel el. Arbeit produziert wird. Die 4
Druckleitungen sind 520 m lang und haben einen
Innendurchmesser von 1,5 m. Es werden 250 000 kWh an
elektrischer Arbeit aus dem Netz entnommen.
Ermittle den Gesamtwirkungsgrad der Anlage (bestehend
aus Motorgenerator, Pumpturbine und Rohrsystem).
geg.: h = 300 m
FG = 200 000 ⋅ 10 kN
= 2 ⋅ 106kN
Wzu = 250 000 kWh =
= 2,5 ⋅ 105kW ⋅ 3600 s
= 9 ⋅ 108 kWs
ges.: (Wab in kWs)
η in %
4.
η=
Pab
Pzu
Pab ⋅t Wab
=
Pzu ⋅t Wzu
Wab = WLage = m ⋅ g ⋅ h = FG ⋅ h = 2 ⋅ 106 kN ⋅ 300 m
=
= 6 ⋅ 108 kNm = 6 ⋅ 108 kWs
6 ⋅ 108 kWs
= 0, 66
η=
9 ⋅ 108 kWs
= 0, 66%
Leroy LineRider aus Cyber-City will mit seinem
Schlitten über einen 5 m hohen Hügel sausen,
dessen Radius 9 m beträgt. Damit die Zentripedalkraft nicht größer als seine Gewichtskraft ist,
darf die Geschwindigkeit dort 9,5 m/s nicht
überschreiten. ar = v2/r
a) Wie hoch darf der 1. Hügel höchsten sein,
damit er nicht am 2. Hügel abhebt? (Reibverluste vernachlässigbar, µ = 0)
9,51 m
b) Wie weit kommt Leroy hinterher auf der sich anschließenden waagerechten
Eisbahn, wenn der Reibungsfaktor µKufen-Eis = 0,015 beträgt?
634 m
Wiederholung 4
a) geg.: v2 = 9,5 m/s
h2 = 5 m
ges.: (∆h in m)
h1 in m
Arbeit, Energie, Wirkungsgrad
WLage = WBewegung
S. 3
m ⋅ g ⋅ ∆h = 1 ⋅ m ⋅v 2
⇒
2
2
(9,5 m / s )
⇒ ∆h = v =
= 4,51 m
2 ⋅ g 2 ⋅ 10 m / s 2
⇒ h1 = 5 m + 4,51 m = 9,51 m
2
v auf dem 2. Hügel entsteht aus
dem Verlust der Lageenergie:
b) geg.: h1 = 9,51 m
µHaft = 0,015 m
ges.: s in m
WLage = WBewegung = WRe ibung
⇒ FG ⋅ h1 = µ ⋅ FN ⋅ s
m ⋅ g ⋅ h1 = µ ⋅ m ⋅ g ⋅ s
h 9,51 m
= 634 m
s = µ1 =
0, 015
5.
Bodo (21 Jahre, 100 kg Lebendgewicht) will Bungee-Jumping von einer 120 m hohen Brücke (über
einen 5 m tiefen Fluss) betreiben.
a) Trage die Bewegung qualitativ in ein v-t-Diagramm ein.
b) Wie lang muss das Gummiseil (das sich um ein Vielfaches seiner Ausgangslänge dehnen kann)
sein, wenn er den Fluss nur mit der Nasenspitzen berühren darf und (dort) max. 3-fache
Erdbeschleunigung erfahren darf?
40 m
a)
Die Energie der Lage baut sich ab; die kin. Energie
steigt. Wenn das Seil sich spannt, baut sich weiter
die Lageenergie ab und geht zum größten Teil in
Spannenergie über.
Am unteren Punkt ist die gesamte Lageenergie in
Spannenergie übergegangen:
b) geg.: h = 120 m
FG = 1000 N
ges.: (D in N/m)
WLage = WSpann
h = 3 ⋅ sFeder
2
⇒ FG ⋅ h = 1 ⋅ Fmax ⋅ sFeder = 1 ⋅ 3 ⋅ FG ⋅ sFeder
2
2
⇒
sFeder = 2 ⋅ h = 2 ⋅ 120 m = 80 m
3
3
3 ⋅ 1000 N
D = ∆∆Fs =
= 37,5 N
m
80 m
s = h − sFeder = 120 m − 80 m = 40 m
Das Gummiseil ist nur 40 m lang und dehnt sich dann bis auf 120 m aus. (Bodos Körperlänge abziehen)
6.
Das skizzierte Spannelement soll eine Kraft von F1=25 kN
aufbringen.
a) Wie groß muss die Kraft in der Spannschraube mit der
Steigung von p=1,5 mm mindestens sein, wenn von der (nicht
unerheblichen) Reibung abgesehen wird?
9,1 kN
(Den einfachsten Lösungsweg wählen!)
b) Welche Lösungsschritte müsste man gehen, wenn man die
Reibung (z.B. µ=0,3) berücksichtigen will? **
Wiederholung 4
a) geg.: F1 = 25 kN
s2 = 1,5 mm
α = 20 O
ges.: (s1 in mm)
F2 in kN
WSchraube = WSpannelement
tan20O =
„Goldene Regel der Mechanik“:
Vergleich der Arbeit von Schraube
und Spannelement bei z.B. einer
Umdrehung:
b)
FR
FR
FR
Arbeit, Energie, Wirkungsgrad
⇒
S. 4
F2 ⋅ s2 = F1 ⋅ s1
s1
O
s2 ⇒ s1 = s2 ⋅ tan20
F ⋅ s F ⋅ s ⋅ tan20O
= F1 ⋅ tan20O = 25 kN ⋅ 0,369
F2 = 1s 1 = 1 2 s
2
2
F2 = 9,1 kN
Uihuihuih...
... man müsste „ins Detail“ gehen und Schritt für Schritt von einem
Bauteil zum nächsten an allen Gleitflächen (aus den jew. FN) die jew.
Reibkräfte ermitteln und daraus die jew. Resultierenden bestimmen.
Na denn „viel Spaß“ dabei.