und Erwartungswert 1

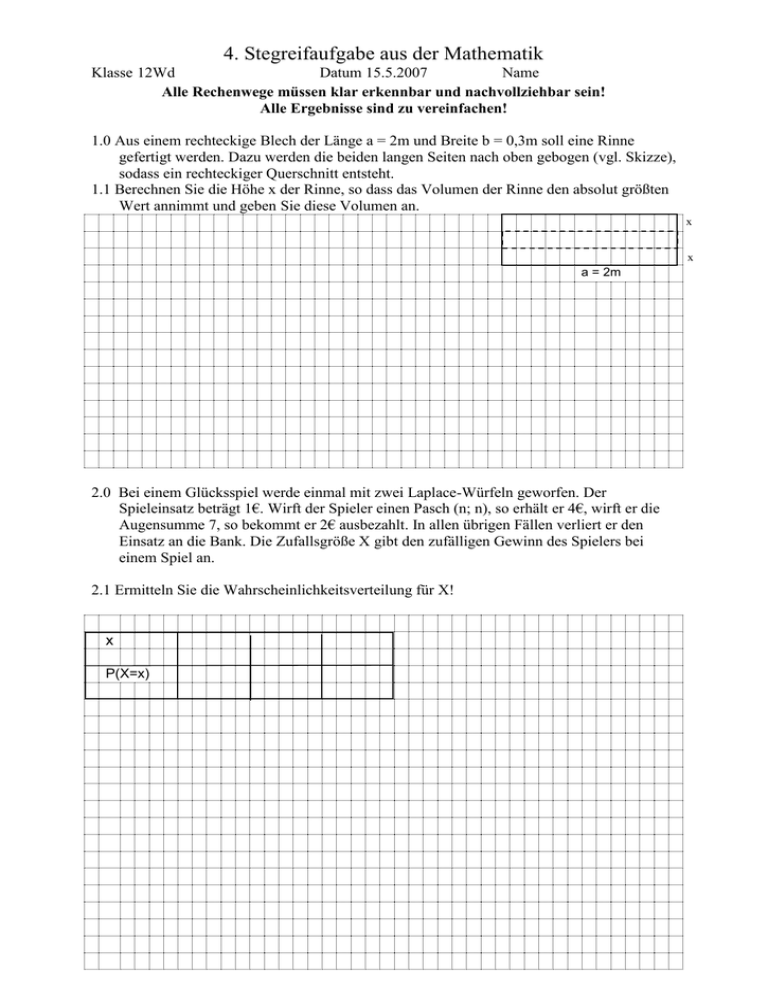
4. Stegreifaufgabe aus der Mathematik
Klasse 12Wd
Datum 15.5.2007
Name
Alle Rechenwege müssen klar erkennbar und nachvollziehbar sein!
Alle Ergebnisse sind zu vereinfachen!
1.0 Aus einem rechteckige Blech der Länge a = 2m und Breite b = 0,3m soll eine Rinne
gefertigt werden. Dazu werden die beiden langen Seiten nach oben gebogen (vgl. Skizze),
sodass ein rechteckiger Querschnitt entsteht.
1.1 Berechnen Sie die Höhe x der Rinne, so dass das Volumen der Rinne den absolut größten
Wert annimmt und geben Sie diese Volumen an.
x
x
a = 2m
2.0 Bei einem Glücksspiel werde einmal mit zwei Laplace-Würfeln geworfen. Der
Spieleinsatz beträgt 1€. Wirft der Spieler einen Pasch (n; n), so erhält er 4€, wirft er die
Augensumme 7, so bekommt er 2€ ausbezahlt. In allen übrigen Fällen verliert er den
Einsatz an die Bank. Die Zufallsgröße X gibt den zufälligen Gewinn des Spielers bei
einem Spiel an.
2.1 Ermitteln Sie die Wahrscheinlichkeitsverteilung für X!
x
P(X=x)
2.2 Berechnen Sie Erwartungswert und Streuung von X!
2.3 Macht die Bank auf lange Sicht gesehen Verlust, Gewinn oder ist es ein faires Spiel?
3.0 Ein Laplace-Würfel wird 100-mal geworfen. Die Zufallsgröße Y gibt die Anzahl der
durch drei teilbaren Augenzahlen unter den 100 geworfenen Augenzahlen an.
3.1 Wie viele durch drei teilbare Augenzahlen sind bei hundert Würfen zu erwarten?
Hinweis: Bestimmen zuerst Sie die Wahrscheinlichkeit für eine durch teilbare Augenzahl
bei einem Wurf !)
3.3 Berechnen Sie die Streuung  von Y!
3.4 Mit welcher Wahrscheinlichkeit liegt Y im Intervall [ − ;  + ]?
Viel Erfolg!!!
4. Stegreifaufgabe aus der Mathematik
Klasse 12Wd
Datum 15.5.2007
Name LÖSUNG
Alle Rechenwege müssen klar erkennbar und nachvollziehbar sein!
Alle Ergebnisse sind zu vereinfachen!
1. Aus einem rechteckige Blech der Länge a = 2m und Breite b = 0,3m soll eine Rinne
gefertigt werden. Dazu werden die beiden langen Seiten nach oben gebogen (vgl. Skizze),
sodass ein rechteckiger Querschnitt entsteht.
1.1 Berechnen Sie die Höhe x der Rinne, so dass das Volumen der Rinne den absolut größten
Wert annimmt und geben Sie diese Volumen an.
V(x) = a∙(b − 2x)∙x = abx − 2ax2  ; x[0;0,15]
V(x) = 0,6x − 4x2
V’(x) = 0,6 − 8x = 0  x = 0,075
V’’(x) = −8 < 0  rel. Maximum bei x = 0,075
V(0) = V(0,15) = 0 
V(0,075) =
(7)
2.0 Bei einem Glücksspiel werde einmal mit zwei Laplace-Würfeln geworfen. Der
Spieleinsatz beträgt 1€. Wirft der Spieler einen Pasch (n; n), so erhält er 4€, wirft er die
Augensumme 7, so bekommt er 2€ ausbezahlt. In allen übrigen Fällen verliert er den
Einsatz an die Bank. Die Zufallsgröße X gibt den zufälligen Gewinn des Spielers bei
einem Spiel an.
2.1 Ermitteln Sie die Wahrscheinlichkeitsverteilung für X!
x
−1
1
P(X=x)
0,778
0,056
3
0,167


1 1 1
(n;n) p1 = p2 = p3 = p4 = p5 = p6 = 6∙   
6 6 6
1 1 1
(4;3), (3;4) : p7 = 2∙   
6 6 18
(4)
2.2 Berechnen Sie Erwartungswert und Streuung von N!
E(N) = −1∙0,778 + 1∙0,056 + 3∙0,167 = −0,22
Var(N) = 1∙0,778 + 1∙0,056 + 9∙0,167 − 0,222 = 2,29
 = 1,51
(3)
2.3 Macht die Bank auf lange Sicht gesehen Verlust, Gewinn oder ist es ein faires Spiel?
Die Bank macht Gewinn.
(1)
3.0 Ein Laplace-Würfel wird 100-mal geworfen. Die Zufallsgröße Y gibt die Anzahl der
durch drei teilbaren Augenzahlen unter den 100 geworfenen Augenzahlen an.
3.1 Wie viele durch drei teilbare Augenzahlen sind bei hundert Würfen zu erwarten?
Hinweis: Bestimmen zuerst Sie die Wahrscheinlichkeit für eine durch teilbare Augenzahl
bei einem Wurf !)
E(X) = 100∙
1
= 33,33
3
(1)
3.2 Berechnen Sie die Streuung  von Y!
1 2
Var(X) = 100∙  = 22,22
3 3
 = 4,71
(2)
3.3 Mit welcher Wahrscheinlichkeit liegt Y im Intervall [ − ;  + ]?
28 < x < 38
p = B(100;0,33;x37) − B(100; 0,33; x  28) = 0,81231 − 0,15241 = 0,6599 
(2)
Summe(20)
Viel Erfolg!!!