Inferenzstatistik I
Werbung

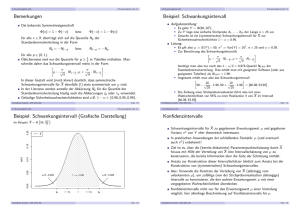
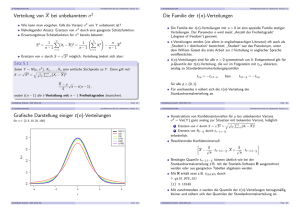
Iran Wiederholung Inferenzstatistik Zusammenfassung Zentraler Grenzwertsatz/Konfidenzintervalle Statistik I Sommersemester 2009 Statistik I ZGWS/Konfidenzintervalle (1/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Kann Ahmadinejad die Wahl gewonnen haben? I Im wesentlichen Dreiteilung der polit. Elite I 2005: 17.3 Millionen Stimmen (Stichwahl), Wahlbeteiligung 48% I 2009: 24.5 Millionen Stimmen, Wahlbeteiligung ca. 83% I Anders als 2005 kaum Unterschiede in Wahlbeteiligung zwischen den 30 Provinzen I Woher kommt der Zuwachs von 7.2 Millionen Stimmen? Statistik I ZGWS/Konfidenzintervalle (2/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Was ist problematisch? I I Etwas über 100% Wahlbeteiligung in zwei konservativen Provinzen In zehn Provinzen müßte Ahmadinejad nach dem offiziellen Ergebnis I I I I I I Alle konservativen Wähler von 2005 Alle Erst-/früheren Nichtwähler Alle früheren Zentrumswähler Und fast die Hälfte der reformistischen Wähler für sich gewonnen haben 1997, 2001 und 2005 konservative Kandidaten in ländlichen Provinzen sehr unpopulär 2009 I I Kein Zusammenhang zwischen Zunahme Wahlbeteiligung/Zunahme Ahmadinejad Negativer Zusammenhang zwischen ländlich/Ahmadinejad verschwindet Statistik I ZGWS/Konfidenzintervalle (3/37) Iran Wiederholung Inferenzstatistik Zusammenfassung 2005: Land/Ahmadinejad Statistik I ZGWS/Konfidenzintervalle (4/37) Iran Wiederholung Inferenzstatistik Zusammenfassung 2009: Land/Ahmadinejad Mehr: http://www.chathamhouse.org.uk/files/14234_iranelection0609.pdf Statistik I ZGWS/Konfidenzintervalle (5/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Wahlbeteiligung/Zuwachs Ahmadinejad Statistik I ZGWS/Konfidenzintervalle (6/37) Iran Wiederholung Inferenzstatistik Zusammenfassung 0.0 0.1 0.2 0.3 0.4 Iran Wiederholung Inferenzstatistik Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Zusammenfassung −4 Statistik I −2 ZGWS/Konfidenzintervalle (7/37) 0 2 4 Iran Wiederholung Inferenzstatistik Zusammenfassung Zum Nachlesen I Agresti/Finlay Kapitel 5 I Gehring/Weins Kapitel 11 I Schumann Kapitel 6 Statistik I ZGWS/Konfidenzintervalle (8/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Zufallsexperiment/Wahrscheinlichkeiten I Zufallsexperiment: I I I Ausgang hängt nur vom Zufall ab (Theoretisch) beliebig oft wiederholbar Relative Häufigkeiten → Wahrscheinlichkeiten I Gedankenexperiment; Standardbeispiele: Münz- und Würfelwurf I Nützliches Modell für Sozialwissenschaftler I Z. B. für Stichprobenziehung Statistik I ZGWS/Konfidenzintervalle (9/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Wahrscheinlichkeitsverteilungen I Wahrscheinlichkeitsverteilungen fassen mögliche Ergebnisse von Zufallsexperimenten und deren Wahrscheinlichkeiten zusammen I Summe der Balken über alle Ereignisse = 1 I Ok für abzählbare Ereignisse (diskrete Zufallsvariablen) I Was tun mit kontinuierlichen Zufallsvariablen? I Histogramm → Dichteschätzung I Fläche unter Dichtefunktion = 1 (Gesamtwahrscheinlichkeit) I Wahrscheinlichkeit für Wert aus einem bestimmten Bereich = Fläche über diesem Intervall Statistik I ZGWS/Konfidenzintervalle (10/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Dauer: Fahrt zur Arbeit Wieviel % der Bürger brauchen 60 Minuten oder weniger für den Weg zur Arbeit? I Potentielle Unterstützer für Infrastrukturmaßnahmen I Fläche links von 60? 0.4 0.2 0.0 Dichte 0.6 I 0 50 100 150 200 250 300 Arbeitsweg in Minuten Statistik I ZGWS/Konfidenzintervalle (11/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Dauer: Fahrt zur Arbeit Wieviel % der Bürger brauchen 60 Minuten oder weniger für den Weg zur Arbeit? I Potentielle Unterstützer für Infrastrukturmaßnahmen I Fläche links von 60? → 37% 0.4 0.2 0.0 Dichte 0.6 I 0 50 100 150 200 250 300 Arbeitsweg in Minuten Statistik I ZGWS/Konfidenzintervalle (11/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Dauer: Fahrt zur Arbeit Wieviel % der Bürger brauchen 60 Minuten oder weniger für den Weg zur Arbeit? I Potentielle Unterstützer für Infrastrukturmaßnahmen I Fläche links von 60? → 37% I Wieviele % brauchen mehr als 10 und weniger als 60 Minuten? 0.4 0.2 0.0 Dichte 0.6 I 0 50 100 150 200 250 300 Arbeitsweg in Minuten Statistik I ZGWS/Konfidenzintervalle (11/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Dauer: Fahrt zur Arbeit Wieviel % der Bürger brauchen 60 Minuten oder weniger für den Weg zur Arbeit? I Potentielle Unterstützer für Infrastrukturmaßnahmen I Fläche links von 60? → 37% I Wieviele % brauchen mehr als 10 und weniger als 60 Minuten? I Wichtige Verteilungen tabelliert 0.4 0.2 0.0 Dichte 0.6 I 0 50 100 150 200 250 300 Arbeitsweg in Minuten Statistik I ZGWS/Konfidenzintervalle (11/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Bekannteste und wichtigste aller kontinuierlichen Zufallsverteilungen 0.2 I Wahrscheinlichkeitsdichte für Werte zwischen −∞ und +∞ I Fläche unter der Kurve =1 I Über dem Intervall [-1;2] liegen rund 82% der Fläche I D. h. in ≈ 4 von 5 Fällen zieht man einen Wert aus diesem Intervall Statistik I 0.1 0.3 0.4 I 0.0 Normalverteilung −4 −2 0 ZGWS/Konfidenzintervalle (12/37) 2 4 Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Worum geht es bei der Inferenzstatistik? I Wie kommt man von einer Stichprobe zu einem (gültigen) Schluß auf die Grundgesamtheit? I Bzw. wie groß ist der Fehler, den man dabei wahrscheinlich macht? I Parameter in der Stichprobe vs. Parameter in der Grundgesamtheit Parameter z. B.: I I I I I I I Mittelwert Varianz/Standardabweichung Anteilswerte Zusammenhangsmaße Regressionskoeffizienten ... Statistik I ZGWS/Konfidenzintervalle (13/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Grundgesamtheit/Stichprobe Parameter“ ” Grundgesamtheit µ σ2 σ Θ ... x̄ s2 s p ... ? Stichprobe Statistik I ZGWS/Konfidenzintervalle (14/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Grundgesamtheit/Stichprobe Parameter“ ” Grundgesamtheit µ σ2 σ Θ ... x̄ s2 s p ... ? Stichprobe Statistik I ZGWS/Konfidenzintervalle (14/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Grundgesamtheit/Stichprobe Parameter“ ” Grundgesamtheit µ σ2 σ Θ ... x̄ s2 s p ... ? Stichprobe Statistik I ZGWS/Konfidenzintervalle (14/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Grundgesamtheit/Stichprobe Parameter“ ” Grundgesamtheit µ σ2 σ Θ ... x̄ s2 s p ... ? Stichprobe Statistik I ZGWS/Konfidenzintervalle (14/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Grundgesamtheit/Stichprobe Parameter“ ” Grundgesamtheit µ σ2 σ Θ ... x̄ s2 s p ... ? Stichprobe Statistik I ZGWS/Konfidenzintervalle (14/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Wie funktionieren Punktschätzungen? I Ein Wert als Schätzung für Parameter in der Grundgesamtheit I Punktschätzungen sollen präzise sein (wenig Variationen über Stichproben) I Punktschätzungen sollen unverzerrt / erwartungstreu“ sein ” (kein bias) I Stichprobenmittelwert: unverzerrte Schätzung für Mittelwert in Grundgesamtheit I Anteilswert in Stichprobe: unverzerrte Schätzung für Anteilswert in Grundgesamtheit Statistik I ZGWS/Konfidenzintervalle (15/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Wie funktionieren Punktschätzungen? I Ein Wert als Schätzung für Parameter in der Grundgesamtheit I Punktschätzungen sollen präzise sein (wenig Variationen über Stichproben) I Punktschätzungen sollen unverzerrt / erwartungstreu“ sein ” (kein bias) I Stichprobenmittelwert: unverzerrte Schätzung für Mittelwert in Grundgesamtheit I Anteilswert in Stichprobe: unverzerrte Schätzung für Anteilswert in Grundgesamtheit I Varianz (Standardabweichung) in Stichprobe: Statistik I ZGWS/Konfidenzintervalle (15/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Wie funktionieren Punktschätzungen? I Ein Wert als Schätzung für Parameter in der Grundgesamtheit I Punktschätzungen sollen präzise sein (wenig Variationen über Stichproben) I Punktschätzungen sollen unverzerrt / erwartungstreu“ sein ” (kein bias) I Stichprobenmittelwert: unverzerrte Schätzung für Mittelwert in Grundgesamtheit I Anteilswert in Stichprobe: unverzerrte Schätzung für Anteilswert in Grundgesamtheit I Varianz (Standardabweichung) in Stichprobe: unterschätzt Varianz in Grundgesamtheit Statistik I ZGWS/Konfidenzintervalle (15/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Was ist los mit der Varianz? I Varianz s 2 in Stichprobe unterschätzt Varianz σ2 um Faktor n−1 n n n−1 I Mit I multiplizieren Berechnung von Stichprobenvarianz als Schätzung für Grundgesamtheit läßt sich vereinfachen: n n−1 Σ(xi − x̄)2 n = × n n−1 Σ(xi − x̄)2 = n−1 σ̂2 = s 2 × I Irrelevant in großen Stichproben Statistik I ZGWS/Konfidenzintervalle (16/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Warum reichen Punktschätzungen nicht? σ̂ = √ σ̂2 I Schätzungen basieren auf Zufallsstichproben I Parameter in Stichprobe sind Zufallsvariablen – kontinuierliche Verteilung um wahren Wert (Grundgesamtheit) I Wahrscheinlichkeit wahren Wert exakt zu treffen = 0 I Wahrscheinlichkeit, Stichprobenwert aus einem bestimmten Intervall zu erhalten? I Analyse der Zufallsverteilung Statistik I ZGWS/Konfidenzintervalle (17/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Wiederholung: Repräsentative Umfrage Def. repräsentativ: Die Repräsentativitätslüge“ ” Meinungsumfragen nennen sich ” oft , repräsentativ‘ tatsächlich ’ aber werden die Befragten meist nach dem Zufallsprinzip ausgewählt (aus Vorwärts“, ” 10/1994, S. 23) Statistik I I Jedes Element der GG hat gleiche I oder angebbare I Wahrscheinlichkeit in die Stichprobe zu gelangen ZGWS/Konfidenzintervalle (18/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Wiederholung: Repräsentative Umfrage Def. repräsentativ: Die Repräsentativitätslüge“ ” Meinungsumfragen nennen sich ” oft , repräsentativ‘ tatsächlich ’ aber werden die Befragten meist nach dem Zufallsprinzip ausgewählt (aus Vorwärts“, ” 10/1994, S. 23) I I Jedes Element der GG hat gleiche I oder angebbare I Wahrscheinlichkeit in die Stichprobe zu gelangen Zufällige Auswahl der Untersuchungsobjekte Statistik I ZGWS/Konfidenzintervalle (18/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Wiederholung: Repräsentative Umfrage Def. repräsentativ: Die Repräsentativitätslüge“ ” Meinungsumfragen nennen sich ” oft , repräsentativ‘ tatsächlich ’ aber werden die Befragten meist nach dem Zufallsprinzip ausgewählt (aus Vorwärts“, ” 10/1994, S. 23) I Jedes Element der GG hat gleiche I oder angebbare I Wahrscheinlichkeit in die Stichprobe zu gelangen I Zufällige Auswahl der Untersuchungsobjekte I Voraussetzung für Inferenzstatistik Statistik I ZGWS/Konfidenzintervalle (18/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Stichprobenziehung als komplexes Zufallsexperiment I I I I I I Zufällige Auswahl von n Befragten Berechnung eines Stichprobenparameters (z. B. Mittelwert LRS) über n Befragte Stichprobenparameter als Ergebnis des komplexen Zufallsexperimentes Experiment (prinzipiell) sehr oft wiederholbar Wahrscheinlichkeit, ein bestimmtes Ergebnis/Ergebnis innerhalb eines bestimmten Wertebereiches zu erhalten Berechenbar, wenn Verteilung der Zufallsvariable bekannt Statistik I ZGWS/Konfidenzintervalle (19/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Stichprobenziehung als komplexes Zufallsexperiment I I I I I I I Zufällige Auswahl von n Befragten Berechnung eines Stichprobenparameters (z. B. Mittelwert LRS) über n Befragte Stichprobenparameter als Ergebnis des komplexen Zufallsexperimentes Experiment (prinzipiell) sehr oft wiederholbar Wahrscheinlichkeit, ein bestimmtes Ergebnis/Ergebnis innerhalb eines bestimmten Wertebereiches zu erhalten Berechenbar, wenn Verteilung der Zufallsvariable bekannt Wie sieht die Verteilung des Stichprobenparameters (z. B. Mittelwert) aus? → Grenzwertsatz“ ” Statistik I ZGWS/Konfidenzintervalle (19/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Stichprobenziehung als komplexes Zufallsexperiment I I I I I I I I Zufällige Auswahl von n Befragten Berechnung eines Stichprobenparameters (z. B. Mittelwert LRS) über n Befragte Stichprobenparameter als Ergebnis des komplexen Zufallsexperimentes Experiment (prinzipiell) sehr oft wiederholbar Wahrscheinlichkeit, ein bestimmtes Ergebnis/Ergebnis innerhalb eines bestimmten Wertebereiches zu erhalten Berechenbar, wenn Verteilung der Zufallsvariable bekannt Wie sieht die Verteilung des Stichprobenparameters (z. B. Mittelwert) aus? → Grenzwertsatz“ ” Bei Konstruktion der Zufallsvariable Mittelwert wirken viele (n) einfache Zufallsvariablen zusammen Statistik I ZGWS/Konfidenzintervalle (19/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Einfaches Zufallsexperiment: n = 1 I I I 0.0 0.1 0.2 0.3 0.4 I Würfel einmal werfen (n = 1), Ergebnis notieren Experiment sehr oft wiederholen Häufigkeit der Werte 1, 2, · · · 6 nähert sich an Verteilung in GG (Gleichverteilung) an ( Gesetz der großen Zahl“) ” 10 Wiederholungen 2 3 4 5 6 Statistik I ZGWS/Konfidenzintervalle (20/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Einfaches Zufallsexperiment: n = 1 I I I 0.00 0.05 0.10 0.15 0.20 I Würfel einmal werfen (n = 1), Ergebnis notieren Experiment sehr oft wiederholen Häufigkeit der Werte 1, 2, · · · 6 nähert sich an Verteilung in GG (Gleichverteilung) an ( Gesetz der großen Zahl“) ” 100 Wiederholungen 1 2 3 4 5 6 Statistik I ZGWS/Konfidenzintervalle (20/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Einfaches Zufallsexperiment: n = 1 I I I 0.00 0.05 0.10 0.15 I Würfel einmal werfen (n = 1), Ergebnis notieren Experiment sehr oft wiederholen Häufigkeit der Werte 1, 2, · · · 6 nähert sich an Verteilung in GG (Gleichverteilung) an ( Gesetz der großen Zahl“) ” 1 000 Wiederholungen 1 2 3 4 5 6 Statistik I ZGWS/Konfidenzintervalle (20/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Einfaches Zufallsexperiment: n = 1 I I I 0.00 0.05 0.10 0.15 I Würfel einmal werfen (n = 1), Ergebnis notieren Experiment sehr oft wiederholen Häufigkeit der Werte 1, 2, · · · 6 nähert sich an Verteilung in GG (Gleichverteilung) an ( Gesetz der großen Zahl“) ” 10 000 Wiederholungen 1 2 3 4 5 6 Statistik I ZGWS/Konfidenzintervalle (20/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Einfaches Zufallsexperiment: n = 1 I I I 0.00 0.05 0.10 0.15 I Würfel einmal werfen (n = 1), Ergebnis notieren Experiment sehr oft wiederholen Häufigkeit der Werte 1, 2, · · · 6 nähert sich an Verteilung in GG (Gleichverteilung) an ( Gesetz der großen Zahl“) ” 100 000 Wiederholungen 1 2 3 4 5 6 Statistik I ZGWS/Konfidenzintervalle (20/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 0.20 Komplexeres Zufallsexperiment: n=2 4 5 6 8 10 10 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (21/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 0.20 Komplexeres Zufallsexperiment: n=2 2 3 4 5 6 7 8 9 10 12 100 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (21/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 Komplexeres Zufallsexperiment: n=2 2 3 4 5 6 7 8 9 10 12 1 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (21/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 Komplexeres Zufallsexperiment: n=2 2 3 4 5 6 7 8 9 10 12 10 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (21/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 Komplexeres Zufallsexperiment: n=2 2 3 4 5 6 7 8 9 10 12 100 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (21/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 0.20 Komplexeres Zufallsexperiment: n=3 7 8 9 10 11 12 13 17 10 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (22/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 Komplexeres Zufallsexperiment: n=3 4 6 7 8 9 11 13 15 17 100 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (22/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.04 0.08 0.12 Komplexeres Zufallsexperiment: n=3 3 5 7 9 11 13 15 17 1 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (22/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.04 0.08 0.12 Komplexeres Zufallsexperiment: n=3 3 5 7 9 11 13 15 17 10 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (22/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.04 0.08 0.12 Komplexeres Zufallsexperiment: n=3 3 5 7 9 11 13 15 17 100 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (22/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.05 0.10 0.15 0.20 Komplexes Zufallsexperiment: n=10 26 29 34 36 38 39 40 10 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (23/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.02 0.04 0.06 Komplexes Zufallsexperiment: n=10 22 27 30 33 36 39 42 47 100 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (23/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.02 0.04 0.06 Komplexes Zufallsexperiment: n=10 17 21 25 29 33 37 41 45 49 1 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (23/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.02 0.04 0.06 Komplexes Zufallsexperiment: n=10 15 20 25 30 35 40 45 50 10 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (23/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle 0.00 0.02 0.04 0.06 Komplexes Zufallsexperiment: n=10 14 19 24 29 34 39 44 49 54 100 000 Wiederholungen Statistik I ZGWS/Konfidenzintervalle (23/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Zentraler Grenzwertsatz I Stichprobenmittelwert: komplexe Zufallsvariable, additiv zusammengesetzt aus n einfachen Zufallsvariablen I Verteilung der Stichprobenmittelwerte aus (theoretisch) unendlich vielen Stichproben nähert sich mit zunehmendem Stichprobenumfang an Normalverteilung an I Mittelwert der Normalverteilung entspricht Mittelwert in GG (kein bias) I Wenn n > 30, Normalverteilung brauchbare Approximation I Unabhängig von Verteilung in GG/Stichproben Statistik I ZGWS/Konfidenzintervalle (24/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Zentraler Grenzwertsatz II Variable Verteilung Ausgangsvariable in GG, z. B. Alter z. B. linkssteil Alter eines Befragten: einfache Zufallsvariable wie in GG (linkssteil) Arithmetisches Mittel des Alters: komplexe Zufallsvariable normalverteilt über viele mögliche Stichproben Statistik I ZGWS/Konfidenzintervalle (25/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Berechnung des Standardfehlers Standardfehler σ σx̄ = √ = n r σ2 n I Je größer Streuung in GG, desto größer Standardfehler I Je kleiner Stichprobenumfang, desto größer Standardfehler I Umgekehrt quadratischer Zusammenhang: Um Standardfehler zu halbieren muß Stichprobenumfang vervierfacht werden Statistik I ZGWS/Konfidenzintervalle (26/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Eigenschaften der Normalverteilung I I Familie; gleiche Form, aber unterschiedliche Lage/Breite (Mittelwert/Streuung) Für alle Normalverteilungen I I I I I Ca. 68% der Fläche über Intervall ± 1 Standardabweichung um Mittelwert Ca. 95% der Fläche über Intervall ± 1.96 Standardabweichungen um Mittelwert Standardnormalverteilung“ (z-Verteilung): Mittelwert = 0, ” Standardabweichung/Varianz=1 → Fläche unter Kurve tabelliert Tabelle für alle Normalverteilungen anwendbar (z-Transformation) Viele andere Zufallsverteilungen gehen für große n in Normalverteilung über Statistik I ZGWS/Konfidenzintervalle (27/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Eigenschaften der Normalverteilung II Dichtefunktion 1 x−µ 2 1 f (x) = √ e− 2 ( σ ) σ 2π I e Eulersche Zahl: 2.718 · · · I π : 3.142 · · · I µ: Mittelwert der Verteilung I σ: Standardabweichung der Verteilung Statistik I ZGWS/Konfidenzintervalle (28/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Konfidenzintervalle I In 95% aller Stichproben ist Stichprobenmittelwert nicht weiter als 1.96 Standardfehler vom wahren Mittelwert entfernt I Intervall von 1.96 Standardfehlern um Stichprobenmittelwert schließt in 95% der Fälle wahren Mittelwert in GG mit ein I Intervallschätzung Statistik I ZGWS/Konfidenzintervalle (29/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Konfidenzintervalle II I Stichprobenmittelwerte nicht standardnormal-, sondern normalverteilt (z-Transformation umkehren) I Streuung in GG muß nach bekannter Formel aus Streuung in Stichprobe geschätzt werden → doppelte Unsicherheit I t-Verteilung (größere Wahrscheinlichkeit für extreme Werte, Freiheitsgrade) I Geht bei großen Fallzahlen in Normalverteilung über Statistik I ZGWS/Konfidenzintervalle (30/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Konfidenzintervalle III I Wahrscheinlichkeit, daß Intervall wahren Wert nicht einschließt: Irrtumswahrscheinlichkeit, α I Wahrscheinlichkeit, daß Intervall wahren Wert einschließt: Vertrauenswahrscheinlichkeit 1 − α, manchmal γ genannt In der Forschungspraxis meistens Vertrauenswahrscheinlichkeiten von 95% oder 99% I I I Symmetrisches Intervall aus (Standard)Normalverteilung Kritische Werte“ ±1.96; ±2.58 ” Statistik I ZGWS/Konfidenzintervalle (31/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall Statistik I ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall I Standardfehler berechnen: σx̄ = Statistik I σ √ n = 2.393 √ 1891 = 0.055 ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall I Standardfehler berechnen: σx̄ = I Kritischen Wert“ suchen ” Statistik I σ √ n = 2.393 √ 1891 = 0.055 ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall I Standardfehler berechnen: σx̄ = I Kritischen Wert“ suchen ” I σ √ n = 2.393 √ 1891 = 0.055 n > 1000 → Normalverteilung als Approximation für t-Verteilung Statistik I ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall I Standardfehler berechnen: σx̄ = I Kritischen Wert“ suchen ” I I σ √ n = 2.393 √ 1891 = 0.055 n > 1000 → Normalverteilung als Approximation für t-Verteilung In Normalverteilungstabelle Wert finden, der links und rechts 5% der Fläche abtrennt Statistik I ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall I Standardfehler berechnen: σx̄ = I Kritischen Wert“ suchen ” I I I σ √ n = 2.393 √ 1891 = 0.055 n > 1000 → Normalverteilung als Approximation für t-Verteilung In Normalverteilungstabelle Wert finden, der links und rechts 5% der Fläche abtrennt ±1.644 → 5% der Fläche über Intervall [−∞; −1.644] + 5% der Fläche über Intervall [1.644; +∞] Statistik I ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: LRS in Schweden I x̄ = 5.822; σ = ˆ2.393; n = 1891; gesucht: 90% Konfidenzintervall I Standardfehler berechnen: σx̄ = I Kritischen Wert“ suchen ” I I I I σ √ n = 2.393 √ 1891 = 0.055 n > 1000 → Normalverteilung als Approximation für t-Verteilung In Normalverteilungstabelle Wert finden, der links und rechts 5% der Fläche abtrennt ±1.644 → 5% der Fläche über Intervall [−∞; −1.644] + 5% der Fläche über Intervall [1.644; +∞] Konfidenzintervall: 5.822 ± 1.644 × 0.055 = 5.822 ± 0.09 = [5.732; 5.912] Statistik I ZGWS/Konfidenzintervalle (32/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Konfidenzintervalle für Anteilswerte I Vorgehensweise im Grunde identisch I Verteilung von Anteilswerten binomial I Kann durch Normalverteilung approximiert werden wenn n × p × (p − 1) > 9 Varianz von Anteilswerten: p × (p − 1) I I I I I Zwei Ausprägungen gleich häufig (p = 0.5) → extreme Heterogentität Je geringer Anteil eines Merkmales, desto homogener Keine Varianz wenn p = 1 Konfidenzintervalle können für relative Häufigkeiten oder Prozente berechnet werden Statistik I ZGWS/Konfidenzintervalle (33/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Beispiel: Wahre Wahlabsicht für FDP I Umfrage mit n = 1221: 7.3% (=0.073) würden FDP wählen I 95% Konfidenzintervall? I 1221 × 0.073 × (1 − 0.073) = 82.63 (> 9) q = 0.744% Standardfehler: σp = 92.7%×7.3% 1221 I I Kritischer Wert“: 1.96 ” Konfidenzintervall: 7.3% ± 1.96 × 0.744% = [5.84%; 8.76%] I Alternativ: mit relativen Häufigkeiten rechnen I Statistik I ZGWS/Konfidenzintervalle (34/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Logik Konfidenzintervall I Über sehr viele Stichprobenziehungen hinweg Normalverteilung der Stichprobenkennwerte um wahren Wert in GG mit Streuung = Standardfehler I 95% aller Stichprobenkennwerte nicht weiter als ± 1.96 Standardfehler vom wahren Mittelwert entfernt I Internvall von ± 1.96 Standardfehlern um Stichprobenmittelwert wird in 95% aller Fälle wahren Mittelwert einschließen I Habe ich persönlich eine der vielen (relativ) guten Stichproben? Statistik I ZGWS/Konfidenzintervalle (35/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Punktschätzungen Zentraler Grenzwertsatz Konfidenzintervalle Logik Standardnormalverteilung I Standardnormalverteilung (z-Verteilung): Mittelwert: 0; Varianz/Standardabweichung: 1 I 95% aller Werte im Intervall ± 1.96 I Alle Normalverteilungen haben gleiche Form I 95% der Werte innerhalb von ± 1.96 Standardfehler (> oder < 1) um jeweiligen Mittelwert Statistik I ZGWS/Konfidenzintervalle (36/37) Iran Wiederholung Inferenzstatistik Zusammenfassung Zusammenfassung I Inferenzstatistik – Schluß von Stichproben auf GG I Funktioniert nur für Zufallsstichproben I Modell für zufällige Abweichungen der Stichprobenkennwerte vom wahren Mittelwert in GG I Konfidenzintervall: Bereich, der mit gewünschter Sicherheit wahren Wert einschließt Nächste Woche: Hypothesentests: I I I I Agresti/Finlay: Kapitel 6+7 Gehring/Weins: Kapitel 12 (Schumann: Kapitel 7.3) Statistik I ZGWS/Konfidenzintervalle (37/37)