M2 Merkblatt 2 (Komplexe Zahlen)

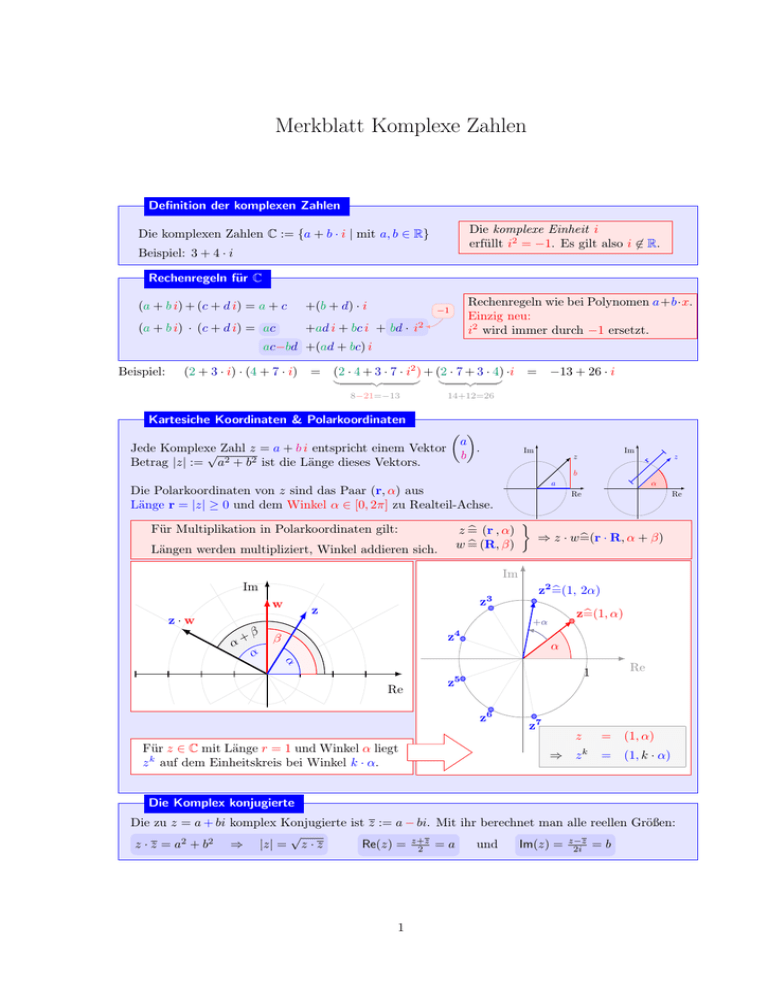
Merkblatt Komplexe Zahlen
Definition der komplexen Zahlen
Die komplexe Einheit i
erfüllt i2 = −1. Es gilt also i 6∈ R.
Die komplexen Zahlen C := {a + b · i | mit a, b ∈ R}
Beispiel: 3 + 4 · i
Rechenregeln für C
(a + b i) + (c + d i) = a + c
+(b + d) · i
(a + b i) · (c + d i) = ac
+ad i + bc i + bd · i2
Rechenregeln wie bei Polynomen a+b·x.
Einzig neu:
i2 wird immer durch −1 ersetzt.
−1
ac−bd +(ad + bc) i
Beispiel:
(2 + 3 · i) · (4 + 7 · i)
=
(2 · 4 + 3 · 7 · i2 ) + (2 · 7 + 3 · 4) ·i
|
{z
} |
{z
}
8−21=−13
−13 + 26 · i
=
14+12=26
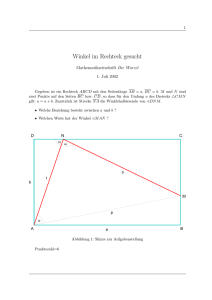
Kartesiche Koordinaten & Polarkoordinaten
a
.
b
Im
Im
z
z
r
Jede Komplexe
√ Zahl z = a + b i entspricht einem Vektor
Betrag |z| := a2 + b2 ist die Länge dieses Vektors.
b
Für Multiplikation in Polarkoordinaten gilt:
Längen werden multipliziert, Winkel addieren sich.
α
a
Die Polarkoordinaten von z sind das Paar (r, α) aus
Länge r = |z| ≥ 0 und dem Winkel α ∈ [0, 2π] zu Realteil-Achse.
Re
z=
b (r , α)
w=
b (R, β)
Re
⇒ z · w=(r
b · R, α + β)
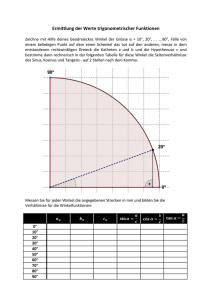
Im
Im
w
z·w
z
z
3
z2 =(1,
b
2α)
z=(1,
b α)
+α
α+
β
z4
β
α
α
α
Re
z6
z7
z
Für z ∈ C mit Länge r = 1 und Winkel α liegt
z k auf dem Einheitskreis bei Winkel k · α.
Re
1
z5
⇒
z
k
=
(1, α)
=
(1, k · α)
Die Komplex konjugierte
Die zu z = a + bi komplex Konjugierte ist z := a − bi. Mit ihr berechnet man alle reellen Größen:
√
z · z = a2 + b2 ⇒ |z| = z · z
Re(z) = z+z
und
Im(z) = z−z
2 =a
2i = b
1
Teilen
Beim Teilen durch eine Komplexe Zahl erweitert man mit der Komplex Konjugierten, um den
Nenner reell zu machen:
w
w·z
w·z
=
=
z
z·z
|z|
i ist nicht
√
2 + 9i
(2 + 9i) · (1 − 2i)
20 + 5i
=4+i
=
= 2
1 + 2i
(1 + 2i) · (1 − 2i)
1 + 22
−1
Die Wurzelfunktion ist nur für nicht-negative
Zahlen aus R definiert, d.h. auch√nach Einführen der
√
Komplexen Einheit i mit i2 = −1 ist “ −1” nicht definiert, und es gilt i 6= −1.
√
−1
√
Die Wurzelfunktion x liefert für x ∈ R mit x ≥ 0 das nicht-negative y, für dass y 2 = x gilt.
Wegen der Einschränkung “nicht-negativ” funktioniert die Wurzelfunktion nicht bei −1:
Warum nicht
• Die Lösungen für y 2 = 16 sind zum Beispiel 4 und −4,
die Wurzelfunktion liefert aber nur die postive Lösung
√
16 = 4.
• Die Lösungen für y 2 = −1 sind i und −i,
aber hier ist (und bleibt!) unklar, wer “die positive” Lösung ist.
Sowohl i als auch −i sind weder positiv noch negativ!
Auch das Argument “i hat kein Vorzeichen” zieht hier nicht, denn: Bei der Definition von C hätte
man (statt die Zahl i zu wählen) ebenso gut die komplexen Zahlen über j := (−i) definieren können!
Dann hätte die Zahl j (also eigentlich −i) “kein Vorzeichen”.
√
Ein anderes,
etwas schwierigeres Argument für i 6= −1 ist das Folgende:
√
Wäre√ −1 eine echte Zahl, so dürfte man also aus −1 √
die Wurzel
d.h. für die entstehende
√
√ ziehen,
Zahl −1 müsste dann die übliche Wurzelrechenregel a · b = a · b gelten.
√
(?)
Annahme: Es gelte i = −1.
√
√ √
(??) Dann gilt die Wurzelrechenregel a · b = a · b auch für a = b = −1.
p
Es gilt dann also: 1)
1 = p(−1) · (−1)
p
??
(−1) · (−1)
2)
⇔ 1 =
?
3)
⇔ 1 = i·i
4)
⇔ 1 = −1
√
Wärend hier 1) unstrittig wahr ist, ist 4) unstrittig falsch, d.h.
√ die Annahme i = −1 führt zu
einem Widerspruch (und zwar durch (??), das direkt aus i = −1 folgt).
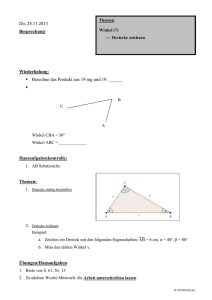
Einheitswurzeln
Die Lösungen der Gleichung z n = 1 sind Punkte
auf dem Einheitskreis zk =(1,
b k · α) mit Winkel
α = 2π/n, wobei gilt k = 0, 1, 2, . . . n − 1. Für
jeden dieser Punkte gilt:
zk =(1,
b k · 2π/n)
=⇒
(zk )n =
b (1, n · k · 2π/n)
=
b (1, k · 2π)
=⇒
(zk )n = 1
Einer der Punkte ist die Zahl z = 1 (bei k =
0), alle weiteren Punkte liegen auf einem Symmetrischen n-Eck.
z5 = 1
Im
z1 =(1,
b α)
z2 =(1,
b 2α)
+α
α
z0 =(1,
b 0)
1
Re
z3 =(1,
b 3α)
α = 2π
5
(72◦ )
z4 =(1,
b 4α)
Dies lässt sich aus den Multiplikationsregeln (Längen multiplizieren, Winkel addieren) für Polarkoor-
2
dinaten folgern. Wir betrachten das Beispiel z 5 = 1:
Die Zahl z hat Polarkoordinaten (r, α), d.h. z 5 hat die Polarkoordinaten (r5 , 5 · α).
• Radius von z:
Aus z 5 = 1 folgt sofort r = 1 (also z auf Einheitskreis), denn wegen den Längenberechnungen
|z 5 | = r5 und |1| = 1 folgt
z5 = 1
⇒
|z 5 | = |1|
⇔
r5 = 1 ⇒ r = 1
denn wegen ”r ist eine Länge” ist r ∈ R und r ≥ 0 (d.h. r ist nicht komplex).
• Winkel von z:
Wegen den Multiplikationsregeln (Winkel addieren!) folgt: z ≡ (1, α) ⇒ z 5 ≡ (1, 5α)
Die Zahl 1 hat Polarkoordinaten (1, β) mit Winkel β ∈ {0, 2π, 2 · 2π, 3 · 2π, . . .}
Es folgt also
5α
5α
5α
5α
=
=
=
=
0 · 2π
1 · 2π
2 · 2π
3 · 2π
oder
oder
oder
oder . . .
D.h. 5α = k · 2π bzw. α = k · 2π/5 mit k ∈ N
– Für k = 0, 1, 2, 3, 4 ergeben sich Punkte auf dem Einheitskreis mit Winkelabstand 2π/5
zueinander (die Ecken eines symmetrischen 5-Ecks!), z.B. die Zahl z = 1 ist diejenige
Lösung mit k = 0, d.h. Winkel α = 0.
– Für k = 5, 6, 7, 8, . . . ergeben sich zwar neue Winkel α, aber nicht neue Lösungen z ∈ C,
denn ab k = 5 wiederholen sich die Ergebniszahlen z, weil sich immer Winkel der Form
“echtes-2π-Fünftel plus Vielfaches-von-2π” ergeben. Die Punkte mit Winkel “echtenFünftel-2π” sind mit k = 0, 1, 2, 3, 4 schon entdeckt, während ”Vielfaches-von-2π” für
Winkelangaben unbedeutend ist! Zum Beispiel gilt wegen 5 · 2π/5 = 2π:
k = 5 heißt
α = 5 · 2π/5
= 2π + 0
ergibt selbes z wie bei k = 0.
k = 6 heißt
α = (5 + 1) · 2π/5 = 2π + 1 · 2π/5 ergibt selbes z wie bei k = 1.
k = 7 heißt
α = (5 + 2) · 2π/5 = 2π + 2 · 2π/5 ergibt selbes z wie bei k = 2.
3