Hysteresekupplungen und Hysteresebremsen

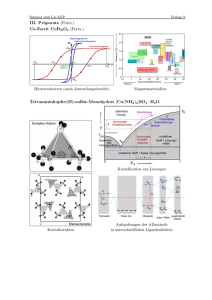
Hysteresekupplungen und Hysteresebremsen
Ein in der Fachliteratur kaum beachtetes Übertragungselement
erlebt eine Renaissance
Dr.-Ing. F. Jurisch, VACUUMSCHMELZE GmbH & Co. KG, Hanau
Kurzfassung
Hysteresekupplungen und -bremsen übertragen berührungslos und unabhängig von der
Drehzahl, der Drehrichtung und der Differenzdrehzahl zwischen An- und Abtriebsteil ein
konstantes Drehmoment. Somit sind sie auch als Haltebremsen geeignet. Der eine Part
fungiert als Erreger eines mehrpoligen magnetischen Feldes, welches das Hysteresematerial
im anderen Teil mehr oder auch weniger stark aussteuert. In dieser Arbeit wird die
Drehmomentbildung hergeleitet, das Zusammenspiel zwischen Erreger- und Hystereseteil
erläutert und ein einfacher Berechnungsweg auf Basis von Abschnittsleitwerten vorgestellt,
der die Abmessungen und Materialeigenschaften berücksichtigt. Die Abhängigkeiten der
geometrischen und konstruktiven Auslegung von den magnetischen Materialeigenschaften
werden beispielhaft berechnet und in Diagrammen dargestellt. Die verschiedenen
konstruktiven Lösungen und Hysteresematerialien mit ihren Vor- und Nachteilen werden
erläutert.
Abstract
The hysteresis clutches and brakes transfer a constant torque without contact and independent from speed, its direction and slip. Therefore they can also be used as stopping brakes.
The hysteresis device consists of two parts. One is an exciter of a magnetic multipolar field
which saturates the hysteresis material in the other part in different grades. This paper
describes the development of torque and the interaction of excitation and hysteresis part. A
simple model of calculation is presented. It is based upon magnetic linear conductances and
allows for geometry dimensions and magnetic properties. The dependencies of geometry and
construction on the magnetic properties are calculated in examples and presented in
diagrams. The different solutions for construction and properties of hysteresis materials and
their advantages and disadvantages are also described.
1. Betriebsverhalten und Anwendung von Hysteresebremsen und -kupplungen
Im Folgenden werden Bremsen und Kupplungen nur noch als Kupplungen bezeichnet. Die
Hysteresekupplung besteht aus einem Erregerteil und dem Hystereseteil, auf welchem sich
das Hysteresematerial befindet. Die Rotationsachsen liegen in einer Flucht. Erreger- und
Hystereseteil können axial aneinander stoßen oder konzentrisch ineinander liegen und sind
durch einen Luftspalt getrennt. Der Erregerteil erzeugt das magnetische multipolare Feld zur
Aussteuerung bis in den gesättigten Zustand des sich auf dem anderen Teil befindlichen
Hysteresematerials.
Drehmoment
200
Hysteresemoment
synchroner Lauf (s = 0)
mit Schlupf (s < 0)
überlastet (Stillstand)
150
Antriebsdrehzahl
100
50
0
0
200
400
600
800
1000
1200 Drehzahl
1400
1600
Bild 1: Auswirkung verschiedener Belastungen auf das Übertragungsverhalten
Eine Hysteresekupplung überträgt berührungsfrei und unabhängig von der Drehzahl n, der
Drehrichtung und der Differenzdrehzahl (Schlupf) ein konstantes Drehmoment (Hysteresemoment Mhys). Ist das Abtriebsmoment Mab kleiner als das Hysteresemoment, dann laufen Anund Abtrieb synchron mit gleicher Drehzahl und gleichem Drehwinkel (Bild 1). Wird das
Hysteresemoment überschritten (Mhys < Mab) tritt ein Schlupf zwischen An- und Abtrieb auf,
der so weit anwächst bis sich auf Grund der Arbeitskennlinie Mab = f(n) ein Momentengleichgewicht Mab = Mhys eingestellt hat. Ist das Abtriebsmoment (= Belastung) weiterhin größer als
das Hysteresemoment, bleibt der Abtriebsteil der Kupplung stehen (nab = 0). Auf Grund dieses
Verhaltens werden Hysteresekupplungen eingesetzt, um Antriebe vor Schäden zu schützen.
Sie arbeiten als Sicherheitskupplung und Drehmomentbegrenzer. Durch die Übertragung
eines von der Differenzdrehzahl unabhängigen konstanten Momentes stellt diese Anordnung
auch eine verschleißfreie Bremse dar. Da dieses Bremsmoment auch bei Schlupf und Drehzahl von Null aufgebaut wird, ist sie auch als Haltebremse geeignet [ 1 ].
Durch eine Veränderung der Erregung mittels Variation des Luftspaltes, der Überdeckung von
Erreger- und Hystereseteil oder der Aussteuerung (Sättigungsgrad) bzw. der Flussführung
kann das Hysteresemoment von einem Maximalwert ausgehend verringert werden. In verschiedenen Ausführungen sogar bis zum Wert Null. Somit kann das Übertragungsmoment in
Stufen oder kontinuierlich eingestellt, geregelt und in einen Regelkreis eingebunden werden.
Besonders einfach lässt sich dies bei einer elektrischen Erregung umsetzen. Bei Permanenterregung sind mechanische Stellglieder erforderlich.
Weit verbreitete Anwendungen finden sich in Auf- und Abhaspeleinrichtungen mit nicht von
der Drehzahl abhängigen regelbaren oder konstanten Faden-, Draht- oder Bandzügen. In
Druckern, Kopierern sowie Geld- und Fahrkartenautomaten schützen Hysteresekupplungen
vor Zerstörung der durch Zahnriemen zentral angetriebenen Transportwellen und Wickelspeicher. Bei letzteren sorgen Hysteresebremsen für die erforderlichen Bandzüge. Die Vorteile
liegen im berührungslosen und somit verschleißfreien Betrieb und bei permanenterregten
Systemen in der Betriebssicherheit, d.h. ohne Energiezufuhr auszukommen.
2. Funktionsprinzip
Die Wirkungsweise der Hysteresekupplung wird aus der Leistungsbilanz der aus An- und
Abtriebsteil bestehenden Anordnung hergeleitet. Es wird eine Axialspaltanordnung mit dem
Erregerteil auf der Antriebsseite und dem Hysteresematerial auf der Abtriebsseite betrachtet.
MAntrieb = MAbtrieb = Mhys = M
MAntrieb
MAbtrieb
nan
nab
Pan = M * Wan
nan – nab = Dn
Pab = M * Wab
f = p*Dn
Pschlupf = Pan – Pab = M * 2p Dn = Pv hys = vh * V * f
Mhys = vh * V * p / 2p
v h = ò BdH = ò HdB = Schleifeni nhalt
Das maximal übertragbare Hysteresemoment wird durch den Flächeninhalt (= Energie) der
voll ausgesteuerten Schleife des Hysteresematerials vh und dessen Volumen V bestimmt und
ist außerdem proportional der Polpaarzahl p des Erregersystems [ 2 ]. Der Hystereseschleifeninhalt vh wird auch als Hysteresebeiwert bezeichnet.
3. Randbedingungen
Hysteresematerial
·
großer Schleifeninhalt vh ≈ 4 * Br * Hc (anisotrop – aber in der richtigen Richtung)
·
aber auch relativ gute magn. Leitfähigkeit (µr ↑) wegen des Erregerbedarfs
·
großes Volumen (Materialdicke s; Durchmesser D; Länge l )
Erregersystem Fsoll = Ferr
·
Hysteresematerial soll innerhalb eines Polwechsels vollständig gesättigt werden
·
hohe Polzahl (aber Sättigungsbedingung beachten)
Fsoll = Jsätt.hys *s * l
Ferr = ap BM* tp * l
≡
BM ≈ Br* hM/(hM + d)
Daraus ergibt sich die Aufgabe, eine optimale Polteilung
tp opt zu finden, bei der alle Teile des
Hysteresematerials beim Durchlaufen von zwei Polteilungen einen vollen Ummagnetisierungszyklus von +Hsätt über Null bis -Hsätt und wieder zum Ausgangspunkt zurück erfahren.
Hierfür wird ein Ersatzschaltbild mit linearen Bauelementen entworfen. Der Ansatz basiert auf
der gerade erreichten Sättigung
des Hysteresematerials durch den Erregerfluss. Der
Feldaufbau kann sowohl permanent als auch elektrisch erregt erfolgen.
4. Magnetisches Ersatzschaltbild für die permanenterregte Ausführung
Das
magnetische
Feld
tritt
senkrecht
ins
H oszillierend
Hysteresematerial ein und läuft dann auf Grund
H rotierend
der guten magnetischen Leitfähigkeit im Band
weiter. Die Sättigung wird nur in der Pollücke
eintreten.
Es
ist
ausreichend,
wenn
alle
Volumenelemente auf einem schmalen Streifen
gesättigt sind. Ein zu starkes Feld würde das
Material schon beim Eintritt voll aussteuern und
eine drehende Magnetisierung mit gesättigtem
Feldvektor hervorrufen. Ein solches Feld bewegt
keine Blochwände mehr sondern lässt nur noch
den
Feldvektor
rotieren.
Drehende
Magnetisierung mit voll ausgesteuertem Feld ruft
Aussteuerung B / Jsätt
keine Hystereseverluste und somit auch kein
Drehmoment mehr hervor [ 3 ]. Zu wenig aber
0%
auch zu viel Feld führt zur Abnahme des
Bild 2: Hystereseverluste bei drehender
Drehmomentes.
20%
40%
60%
80% 100% 120%
und wechselnder Magnetisierung
Bild 3: Modell
Hysteresematerial
s
Js ; Brh ; Hc ; s
hM
aM (=b M/tp) ; d
tp
Erregermagnet
BrM ; hM ; aM
bM
Bild 4: Ersatzschaltbild
R’sa = 1,895 / µ0
R’Hy = 2tpHc / s(Js + Brh)
R’si = (1- ap)tp / 2m0d
R’d = 2d / m0aptp
R’ds = 1,895 / µ0
R’M = 2hM / µ0µpaptp
QM = BrM hM / µ0µp
m hys . sätt =
( J s + B rh ) / 2
2H c
5. Materialwahl
Aus dem Kompromiss eines hohen Schleifeninhaltes und des Sättigungs-Erregerbedarfes
muss die Verlustziffer vh hauptsächlich aus einer großen Remanenzinduktion Br geholt
werden. Metallisch kompakte Magnetwerkstoffe auf Co-Basis und einer rechteckförmigen
Schleife auf Grund einer Vorzugsrichtung (Anisotropie) sind besonders geeignet. Zur
ausreichenden Sättigung des Materials benötigt man ein Feld, welches ca. der doppelten
Koerzitivfeldstärke Hc entspricht. Um die dafür erforderliche Erregung noch aufbringen zu
können, beschränkt sich die Auswahl auf halbharte Magnetwerkstoffe mit Hc < 600 A/cm wie
AlNiCo, FeCrCoMo (CROVAC) und CoFeV (MAGNETOFLEX) [ 4 und 5 ].
AlNiCo-Werkstoffe werden gegossen oder pulvermetallurgisch gesintert hergestellt. Dies führt
zu relativ großen Wandstärken eines spröden, harten und nur durch Schleifen bearbeitbaren
Materials. Die Herstellung einer circumpheralen (tangentialen) Vorzugsrichtung ist sehr
schwierig, deshalb werden meist nur isotrope Materialien eingesetzt. In anisotroper
Herstellung würde man Hysteresebeiwerte bis 325 µWs/mm³ erreichen. Isotrop sind es nur
maximal 150 µWs/mm³. Speziell für Hysteresemotoren entwickeltes höherpermeables
Material auf Basis AlNiCo liegt nur bei 25 bis 50 µWs/mm³.
Die verformbaren FeCrCo- und CoFeV-Werkstoffe haben den Vorteil, dass sie in dünnen
Bändern gewalzt, in Scheiben gestanzt, zu Ringen gerollt oder sogar zu Töpfen tiefgezogen
werden können. Im abschließenden Glühprozess werden die Materialien magnetisch und
auch mechanisch hart. Die Koerzitivfeldstärke und somit der Schleifeninhalt können durch
den Glühprozess eingestellt werden. Beim CROVAC wird eine Anisotropierung durch eine
Magnetfeldglühung ähnlich wie beim AlNiCo erreicht [ 5 ].
Magnetoflex weist eine Walzanisotropie auf. Bei diesem Material kann der Schleifeninhalt
besonders gut durch die Glühtemperatur eingestellt werden (siehe Bild 2).
300
1.2
Br [T]
250
1.0
Hc [A/cm]
200
0.8
150
0.6
100
0.4
50
0.2
Anlasstemperatur TA [ °C ]
0
450°
0.0
475°
500°
525°
550°
575°
600°
625°
650°
675°
700°
Bild 5: Hc und Br als Funktion der Anlasstemperatur bei MAGNETOFLEX 35 U
In Tabelle 1 sind die Kennwerte der wichtigsten Hysteresewerkstoffe und in Tabelle 2 die
Remanenzen der in den Erregersystemen eingesetzten Dauermagnete zusammengestellt.
Tabelle 1: Kennwerte der wichtigsten Hysteresewerkstoffe [ 4 und 5 ]
Material
Br [ T ]
Hc [A/cm]
AlNiCo isotr.
0,8 …1,2 100…600
vh [ µWs/mm³ ] Jsätt. [ T ]
Dichte [g/cm²]
25 … 325
1,2 … 1,4
7,1 … 7,4
CROVAC12/500 aniso 1,15
< 450
< 210
1,35
7,6
CROVAC 12/160 isotr. 0,90
< 360
< 130
1,35
7,6
MAGNETOFLEX 35 U 0,85
< 280
< 90
1,15
8,1
Tabelle 2: Remanenzwerte der wichtigsten Permanentmagnete [ 6 und 7 ]
Material
Remanenz Br [ T ] Material
Remanenz Br [ T ]
Hartferrit isotrop
0,18 … 0,22
NdFeB gespritzt (iso)
0,45 … 0,60
Hartferrit anisotrop
0,38 … 0,44
NdFeB gepresst (iso)
0,62 … 0,74
Ferrit gespritzt (aniso)
0,24 … 0,29
NdFeB gesintert (aniso)
1,10 … 1,40
Der Temperaturkoeffizient der Remanenzinduktion beträgt für
Ferrit:
TK(Br) = -0,2 %/K
NdFeB:
TK(Br) = -0,1 %/K
und
6. Abhängigkeiten der optimalen Polteilung
Die optimale Polteilung legt die Eintrittsbreite des magnetischen Flusses fest, der dann zur
Sättigung der Hysteresematerialdicke s beitragen soll. Demzufolge gibt es einen direkten
linearen Zusammenhang der optimalen Polteilung von der Sättigungspolarisation Jsätt. und der
Dicke des Hysteresematerials. Die Remanenzinduktion BrM und die Polbedeckung ap des
Permanentmagneten gehen reziprok linear ein. Eine Änderung der Magnetdicke hM oder des
Luftspaltes d haben je nach daraus resultierender Veränderung des Arbeitspunktes Einfluss
auf die optimale Polteilung. Der Zusammenhang ist reziprok und im Einfluss proportional zur
Scherung. Die Koerzitivfeldstärke Hc des Hysteresematerials ruft nur über ihren Einfluss auf
die magnetische Leitfähigkeit Änderungen hervor. Da der magnetische Spannungsabfall aber
wesentlich durch Luftspalt und Streuung bestimmt wird, ist der Einfluss sehr gering. Die
Remanenzinduktion des Hysteresematerials Br
hys
steht in einem direkten Verhältnis zur
Sättigungspolarisation und wird deshalb nicht extra untersucht.
Für die Berechnung der Abhängigkeiten basiert das geometrievariable Erregersystem auf
NdFeB-Einzelmagneten (gesintert) mit Br = 1,20 T und 5 mm Höhe bei 70 % Polbedeckung
und das Hysteresematerial auf isotropem, 1,0 mm dicken CROVAC 12/160 mit Hc = 350 A/cm
und Jsätt. = 1,30 T. Die isotropen kunststoffgebundenen Magnete werden meist vielpolig lateral
magnetisiert ausgeführt und es liegt eine Halbachkonfiguration des Erregerfeldes vor. Die
Magnetgeometrie ist dadurch in einigen Freiheitsgraden eingeschränkt. Mit der Polteilung
werden gleichzeitig die Polbedeckung und die Magnethöhe festgelegt. Das Erregersystem
besitzt somit nur noch den Freiheitsgrad der Remanenzinduktion. Für die Parameterstudie der
Halbachanordnung
wurde für die Erregung kunststoffgespritztes Hartferrit
mit einer
Remanenz von Br = 0,285 T sowie für das Hysteresematerial MAGNETOFLEX 35 U mit einer
Koerzitivfeldstärke von Hc = 250 A/cm in einer Dicke von 0,31 mm zu Grunde gelegt. Der
Luftspalt beträgt 1,0 mm.
Die optimale Polteilung bildet die Grundlage für das Festlegen der Polpaarzahl p, einer der
bestimmenden Größen zur Berechnung des maximalen Übertragungsmomentes. Entweder
wird die Polpaarzahl aus den zur Verfügung stehenden Platzverhältnissen (mittlerer Luftspaltdurchmesser D) berechnet oder bei vorgegebener Polzahl der Luftspaltdurchmesser D des
Systems festgelegt.
p = p*D/2tp opt.
D = (2p/p)* tp opt.
oder
Die Abhängigkeit der optimalen Polteilung eines Einzelmagneterregersystems von:
16
20
tp
t p opt
opt.
14
16
12
12
10
8
8
Br [ T ]
6
4
0.4
0.6
0.8
1.0
1.2
1.4
0
1.6
1
2
3
4
5
6
7
hM
Bild 6: der Remanenzinduktion und
Bild 7: der Magnethöhe des Magneten
10
40
tp
tp
opt.
Polbedeckung
opt.
50 %
30
8
8
70 %
90 %
20
100 %
6
Jsätt. [ T ]
4
10
Dicke s [ mm ]
0
0.8
1.0
1.2
1.4
Bild 8: der Sättigungspolarisation Jsätt.hys
2
4
6
8
Bild 9: der Dicke bei versch. Polbedeckung
9.0
7.6
tp
0
1.6
tp
opt.
8.5
7.5
opt
8.0
7.5
7.4
7.0
7.3
Hc [ A/cm ]
7.2
100
6.5
d / mm
6.0
200
300
400
500
600
700
Bild 10: der Koerzitivkraft des Hysteresemat.
0.0
0.5
1.0
1.5
Bild 11: der Luftspaltweite
2.0
2.5
3.0
Für die Halbachanordnung ergeben sich analoge Abhängigkeiten der opt. Polteilung von:
12
12
tp
tp
opt.
10
8
opt.
8
6
4
4
0
0.0
0.2
0.4
0.6
Br [ T ] 0.8
Bild 13: der Remanenz des Magneten
s [ mm ]
2
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Bild 14: der Dicke des Hysteresematerials
7. Konstruktionsprinzipien
Das Grundprinzip basiert auf einer Anordnung alternierender Pole, denen gegenüber sich das
Hysteresematerial befindet. Der vom Polsystem erregte magnetische Fluss tritt über den
Luftspalt in das Hysteresematerial ein und fließt in diesem zu den benachbarten Polen, wobei
er in der Pollücke das Material vollständig bis in die Sättigung aussteuern muss.
Man unterscheidet die Zentraldrehanordnung mit radialem und die Stirndrehanordnung mit
axialem Luftspalt. Vom Prinzip her können beide Anordnungen sowohl permanentmagnetisch als auch elektrisch erregt werden. Der Aktivteil des Hysteresematerials ist beim
Radialluftspalt die Mantelfläche eines (gerollten) Ringes oder eines tiefgezogenen Topfes,
beim Axialluftspalt die Stirnfläche eines Kreisringes (Scheibe mit oder ohne Loch).
Wenn anisotropes Material zum Einsatz kommen soll, so muss die Vorzugsrichtung in beiden Fällen tangential (in Umfangsrichtung) verlaufen. Bei höheren Polzahlen (2p > 8) kann
man mit einem diametral vorzugsgerichteten Ring einen höheren Schleifeninhalt und somit
größere Übertragungsmomente als mit isotropem Material erzielen, ohne hohe Oberwellenmomente mit in Kauf nehmen zu müssen. Senkrecht zur Vorzugsrichtung ausgesteuertes
anisotropes Material hat noch geringere Schleifeninhalte als isotropes Material gleicher
Materialbasis.
Bei der Permanenterregung kann durch Verschieben der beiden Partner der axiale Luftspalt
vergrößert und somit das Moment verringert werden. Bei radialem Spalt wird durch ein axiales
Verschieben die Überdeckung und somit das Moment verringert.
Bei der Axialluftspaltanordnung tritt generell ein großer und bei der Zentraldrehanordnung ein
mit der Verschiebung steigender axialer Zug auf, der in den Lagern abgefangen werden
muss. Er kann aber auch gezielt zur Lagefixierung des sich drehenden Teils ausgenutzt
werden.
Joch
S
N
N
S
S
N
N
Hysteresescheibe
Luftspalt
Magnet
S
Bild 15: Stirndrehkupplung mit axialem Luftspalt
Hysteresematerial
Magnet
Welle
Bild 16: Zentraldrehkupplung mit radialem Luftspalt
Bei der sgn. Doppelanordnung befinden sich zwei Erregerpolsysteme durch Luftspalte
getrennt an beiden Seiten des Hysteresematerials. Von der Berechnung her kann man zwei
Einfachsysteme mit der halben Hysteresematerialdicke
ohne Streufluss auf der dem
Erregersystem abgewandten Seite konfigurieren. Das maximale Übertragungsmoment Mmax
ergibt sich, wenn sich gleichnamige Pole gegenüber stehen. Durch Verdrehen um eine
Polteilung kann das Moment bis auf einen Minimalwert Mmin verringert werden. Die Änderung
verläuft annähernd sinusförmig mit der Verdrehung a.
M(a) = ½ (Mmax + Mmin) + ½ (Mmax – Mmin) cos(pa)
Die axiale Verschiebung oder das Verdrehen bei der Doppelanordnung wird auch zur
Justierung auf bestimmte Übertragungsmomente bei permanentmagnetisch erregten
Systemen genutzt.
Bild 17: Doppelsystem mit axialem Luftspalt
Mit einer elektrischen Erregung kann über den Erregerstrom das Übertragungsmoment von
nahezu Null (nur nach Wechselfeldentmagnetisierung möglich) kontinuierlich bis zum
Maximalmoment verändert werden [ 8 ]. Beim Abregeln ist zu beachten, dass der Strom nur
langsam bei schlüpfender Anordnung (s ≠ 0) verringert werden darf. Anderenfalls werden
Oberwellenmomente auf Grund des Restmagnetismus im Hyseresematerial erzeugt.
Einzelheit Z
Bild 18: Prinzip der elektrisch erregten Hysteresebremse
In der oben skizzierten elektrisch erregten Anordnung entspricht die Polzahl der Gesamtzahl
der Zähne. Auch bei der Auslegung dieses Systems ist auf die Abhängigkeiten der optimalen
Polteilung zu achten. Da elektrisch leicht übererregt werden kann, besteht die Gefahr des
Abgleitens in den Bereich der drehenden Magnetisierung. Das Verhältnis Zahn/Lücke sollte
größer 1 sein und kann bis 2 betragen. Diese Bremsen können sehr dynamisch wechselnde
Lasten aufbauen.
8. Hinweise zur Auslegung
Es ist zu beachten, dass die Kupplung nur im synchronen Lauf bei Schlupf s = 0 keine
Leistung im Hysteresematerial umsetzt. Wenn eine Differenzdrehzahl auftritt oder ein Teil
stehen bleibt, wie es bei Bremsen generell der Fall ist, treten je nach Drehmoment M und
Schlupfdrehzahl n Verluste auf, die entweder im Dauerbetrieb über geeignete Kühlung
abgeführt oder im Kurzzeitbetrieb adiabatisch von der Wärmekapazität c des Hysteresematerials aufgenommen werden kann. Das Hysteresematerial erleidet im Allgemeinen keine
Schädigung, da diese Werkstoffe bis mindestens 450°C beständig sind, aber der Träger (in
vielen Fällen aus Kunststoff) und die benachbarten Magnete oder Wicklungen einschließlich
der verwendeten Kleb- und Isolierstoffe sind meist nur für 120°C und bis 180°C ausgelegt.
Die Verluste Pv ergeben sich nach der zugeschnittenen Größengleichung zu:
Pv [ W ] = 1,05 M [ Ncm ] * n [1000 / min ]
Die Übertemperatur Tü resultiert aus dem Wärmeübergangskoeffizienten ath und der Wärme
abführenden Oberfläche O auf Grund dieser Verlustleistung zu:
Tü = Pv / ( ath*O )
Für rotierende Körper in ruhender Luft beträgt ath = 0,02 … 0,03 W/Kcm². Für die Berechnung
der thermischen Zeitkonstante tth = (c*m)/(ath*O) zur Abschätzung der Erwärmung im
Kurzzeitbetrieb werden noch die spezifische Wärme c und die Dichte g der Hysteresewerkstoffe für die Berechnung der Masse m benötigt [ 9 ]. Die spezifische Wärmekapazität dieser
Werkstoffe beträgt ca. 460 ±20 J / (kg * K). Die Dichten sind Tabelle 1 zu entnehmen.
9. Literaturverzeichnis
[1]
Koch, J.; Ruschmeyer, K.; „Permanentmagnete II“, Boysen & Maasch , HH 1982
[2]
Schüler, K.; Brinkmann, K.; „Dauermagnete“, Springerverlag, Berlin, Heidelberg 1970
[3]
Gössel, K.; „Magnetische Eigenschaften quasiisotroper Elektrobleche bei elliptischer
Magnetisierung“ TU Dresden, Sektion 11 Elektrotechnik
1973
[4]
„Dauermagnetische Werkstoffe“ Firmenschrift, Krupp Widia , Essen 1989
[5]
„Verformbare Dauermagnete“, Firmenschrift PD-003, Vacuumschmelze, Hanau 1999
[6]
„Kunststoffgebundene Dauermagnete“, Firmenschrift Max Baermann, Berg. Gladbach
[7]
„Selten-Erd-Dauermagnete“, Firmenschrift PD-002, Vacuumschmelze, Hanau 2003
[8]
Jordan, H. u.a., „Die Hysteresekupplung, ein neues Übertragungselement“,
ETZ 86 (1965) 6 S. 385-390
[9]
Philippow, E. u.a., TB “Elektrotechnik“ Bd. 1 u.2, Verlag Technik, Berlin 1970